Алгоритмическое и программное обеспечение для решения задач обработки статистической информации

1.

И.П. Симаков
Презентация лекции
на тему:
Алгоритмическое и программное обеспечение
для решения задач обработки статистической
информации о наработках и отказах объектов
при эксплуатации
1

2. ЦЕЛИ И ЗАДАЧИ РАБОТЫ

Цель работы - развитие вычислительных процедур и алгоритмов и
разработка программного обеспечения статистической обработки
информации, получаемой из сферы эксплуатации, для решения задач
объективной оценки характеристик и показателей надежности оборудования
с использованием методов моментов и максимального правдоподобия для
полных и цензурированных выборок без обращения к огромному числу
таблиц.
Задачи работы:
1. Анализ и практическое освоение известных классических методов и
алгоритмов обработки статистических данных для информационноаналитических систем различного назначения.
2. Разработка эффективных алгоритмов и программ реализации методов
моментов и максимального правдоподобия для обработки статистической
информации по полным и цензурированным выборкам.
3. Отработка алгоритмов и программ статистической проверки гипотез о
теоретическом законе распределения с применением критерия согласия
А.Н. Колмогорова и системы неравенств, устанавливающих
принадлежность функции распределения к классу функций с возрастающей
интенсивностью «опасности» (или интенсивностью отказов для
технических систем).
4. Решение конкретных задач обработки экспериментальных (наблюдаемых)
данных с «распознаванием» теоретической функции распределения и
оценкой ее параметров.

3.

Расчет оценок начальных и центральных моментов
по выборке независимых наблюдений t1 ,..., t N над случайной величиной
1. Оценки первых четырех начальных выборочных моментов
mˆ k
1
N
N
t
k
i
k 1,2,3,4,...
2. Оценки первых четырех центральных моментов 1 , 2 , 3 , 4
по известным связующим соотношениям между ними
1 T mˆ 1
2 mˆ 2 mˆ 12
i 1
- математическое ожидание случайной величины
- дисперсия
3 mˆ 3 3mˆ 1mˆ 2 2mˆ 13
- характеристика асимметрии распределения
4 mˆ 4 4mˆ 1mˆ 3 6mˆ 12 mˆ 2 3mˆ 14
- характеристика островершинности
3. Оценки центральных моментов по выборке
ˆ 2 Dˆ
1
ˆ ) 2 ; ˆ 1
ˆ ) 3 ; ˆ 1
ˆ ) 4 ; Skˆ ˆ 3 ; Exˆ ˆ 4 3.
(
t
T
(
t
T
(
t
T
i
i
i
3
4
N i
N i
N i
ˆ 3
ˆ 4
4. Расчет несмещенных центральных моментов
N
1 N
(ti Tˆ )2 ; ˆ H ˆ 2 H
N 1 i 1
1
Tˆ
N
ti ; ˆ 2 H
ˆ 3 H
N2
N ( N 2 2 N 3) ˆ 4 3N (2 N 3) ˆ 22 Skˆ
ˆ
3 ; ˆ 4 H
;
H
( N 1)( N 2)
( N 1)( N 2)( N 3)
i 1
N ( N 1) ˆ
Sk ;
N 2
Exˆ H
N 1
( N 1) Exˆ 6 .
( N 2)( N 3)
3

4.

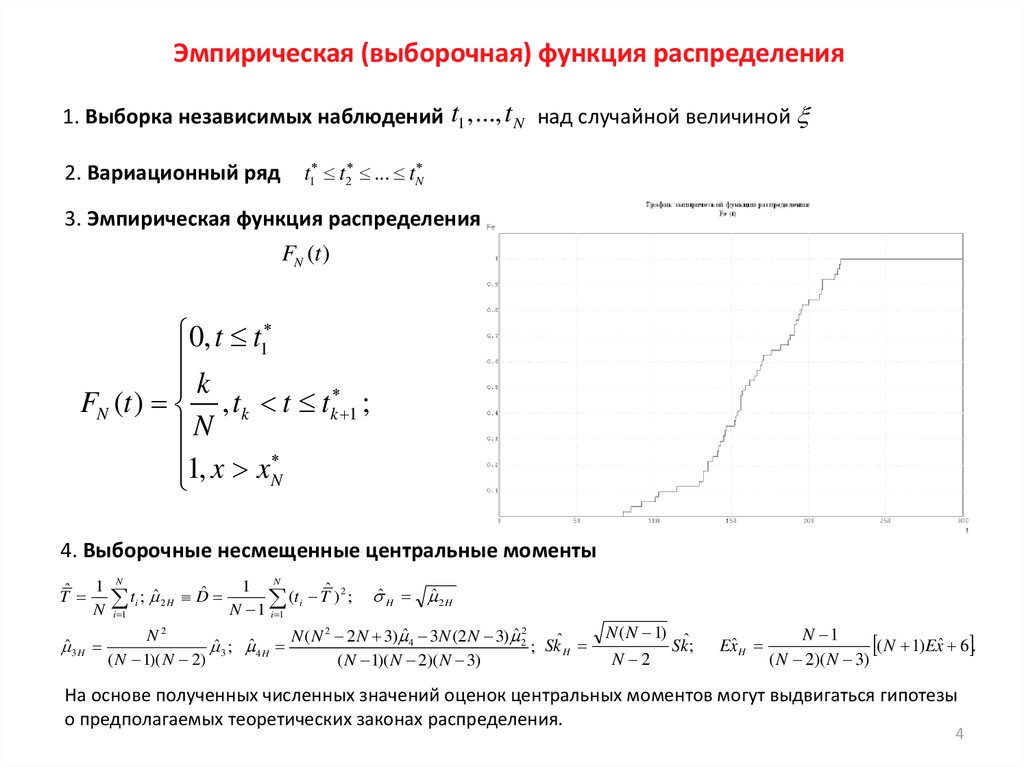
Эмпирическая (выборочная) функция распределения
1. Выборка независимых наблюдений t1 ,..., t N над случайной величиной
2. Вариационный ряд
t1 t2 ... t N
3. Эмпирическая функция распределения
FN (t )
0, t t1
k
FN (t ) , tk t tk 1 ;
N
1, x xN
4. Выборочные несмещенные центральные моменты
N
1 N
(t i Tˆ ) 2 ;
N 1 i 1
1
Tˆ
N
ti ; ˆ 2 H Dˆ
ˆ 3 H
N2
N ( N 2 2 N 3) ˆ 4 3N (2 N 3) ˆ 22
ˆ 3 ; ˆ 4 H
; SkˆH
( N 1)( N 2)
( N 1)( N 2)( N 3)
i 1
ˆ H ˆ 2 H
N ( N 1) ˆ
Sk ;
N 2
Exˆ H
N 1
( N 1) Exˆ 6 .
( N 2)( N 3)
На основе полученных численных значений оценок центральных моментов могут выдвигаться гипотезы
о предполагаемых теоретических законах распределения.
4

5.

Метод моментов
для точечной оценки неизвестных параметров заданного распределения
Метод моментов предложен в 1894 г..
Карлом Пирсоном (1857 – 1936) английский математик-статистик,
биолог, философ, основоположник
знаменитого журнала «Биометрика».
Идея метода проста - приравнивание теоретических моментов
соответствующим эмпирическим моментам того же порядка.
Если распределение определяется двумя параметрами, то
приравнивают два теоретических момента двум соответствующим
эмпирическим моментам того же порядка. Заметим – метод не
использует информацию о третьем и четвертом выборочных моментах.
5

6.

Метод моментов
для точечной оценки неизвестных параметров заданного распределения
1. Для нахождения двух неизвестных параметров a и b распределения Вейбулла
a 1
a 1
t a
t a
a t
a
t
F (t ) 1 exp - , f (t ) exp , (t ) ,
b
b b
b b
b
достаточно использовать два первых соотношения:
T b (1 1a ),
D b2 (1 a2 ) (1 1a ) ,
2
заменив теоретические значения моментов их выборочным несмещенным оценкам.
Выражая b из соотношения для первого момента и подставляя во второе соотношение,
получаем сложное алгебраическое уравнение для нахождения параметра а
2
1 2 2 1
D ((T ) / Г (1 )) 1 1 ,
a
а a
где (x ) — гамма-функция или Эйлеров интеграл второго рода
( x) t x 1 e t dt ,
0
численные значения которого заданы таблично в интервале1 x 2 .
Значком «тильдой» означают выборочные моменты.
6

7.

Метод моментов
для точечной оценки неизвестных параметров заданного распределения
2. Для нахождения двух неизвестных параметров a и Гамма - распределения с
плотностью вероятности наработки до отказа
f (t )
где
— параметр масштаба (
a
( a )
0
),
t a 1 e t ; t 0,
a — параметр формы ( a 0 ),
(a ) — Эйлеров интеграл второго рода (a) t a 1 e t dt
0
T2 T ,
решение задачи таково a
,
D
D
где в правые части подставляются соответственно выборочные оценки
математического ожидания и дисперсии
1
Tˆ
N
N
t ;
i 1
i
Dˆ
1 N
(ti Tˆ ) 2 .
N 1 i 1
(Заметим – метод не использует информацию о третьем и четвертом
выборочных моментах)
7

8.

Метод максимального правдоподобия
для точечной оценки неизвестных параметров заданного распределения
Предложен в 1912 г. Рональдом Айлмер Фишером (1890 -1962) - английский генетик,
математик-статистик внес огромный вклад в теорию вероятностей и математическую
статистику, является родоначальником дисперсионного анализа и вместе с К.Пирсоном
заложил основы теории проверки статистических гипотез.
Идея метода такова.
1. Получена из генеральной совокупности полная выборка t1, t2 ,..., t N
- совокупность возможных значений независимых, одинаково
распределенных случайных величин.
2. Принимается гипотеза о виде функции распределения или
плотности вероятности f (t ; a, b) , где а и b - параметры, подлежащие
определению.
3. Вероятность получения выборки t1 , t 2 ,..., t N равна: f (t1 ; a, b) f (t 2 ; a, b)... f (t N ; a, b)dt1dt 2 ...dt N ,
N
4. Вводится функция правдоподобия L(t1 ,..., t N ; a, b) ,f (ti ; a, b)
i 1
которая должна быть максимизирована по параметрам ( a, b) .
Удобно использовать функцию ln L(t1 ,..., t N ; ) , имеющую максимум в той же точке, что и
L(t1 ,..., t N ; a, b) .
(ln L(t ,..., t ; )) 0
Необходимые условия оптимальности имеют вид:
1
N
a
(ln L(t1 ,..., t N ; )) 0
a
Решение системы алгебраических уравнений дает оптимальные (aˆ , bˆ).
При выполнении достаточно общих условий эти оценки являются состоятельными и асимптотически эффективными.
В общем случае оценки (aˆ , bˆ) являются смещенными (см. на с. 544 в кн. Крамер Г. «Математические методы
статистики». – М.: Мир, 1975. – 648 с.).
8

9.

Метод максимального правдоподобия
для точечной оценки неизвестных параметров заданного распределения
1. Для экспоненциального распределения с плотностью вероятности f (t , ) e t
функция правдоподобия имеет вид L(t1 ,..., t N ; ) e
N
N
ti
i 1
N
или ln L(t1 ,..., t N ; ) N ln ti .
ln L(t1 ,..., t N ; ) N N
ti 0,
Необходимое условие экстремума при этом имеет вид
i 1
1
из которого находим решение ˆ
N
1
.
ˆ
T
1
ti
N i 1
2. Для нормального распределения с плотностью
N
N
функция правдоподобия
ln L(t1 ,..., t N ; T , ) N ln ln
2
N
2
2
i 1
2
или
1 ti T
i 1
.
2
2
N
1 t T
1
f (t , T , )
e 2
2
t i T
1
1 2
L(t1 ,..., t N ;T , )
e
2
1
i 1
2
Необходимые условия экстремума
ln( L(t1 ,..., t N ;T , ))
T
ti NT
i 1
2
t T
N
N
0,
ln( L(t1 ,..., t N ; T , ))
1 N
2
2
Решение этой системы алгебраической уравнений
i 1
2
i
2 4
0
2
1 N
1 N
2
ˆ
ˆ
T ti и ˆ ti T .
N i 1
N i 1
9

10.

Метод максимального правдоподобия
для точечной оценки неизвестных параметров заданного распределения
Для Гамма – распределения с плотностью вероятности
( t )a -1 t
f (t; ) =
e ; (t 0; a 0, 0)
(a)
N
N
a 1
Функция правдоподобия L(t1,..., t N ; , a) =
ti e t i , или эквивалентная ей
(a) i 1
N
N
i 1
i 1
ln( L(t1 ,..., t N ; , a)) N a ln( ) N ln( (a)) (a 1) ln( ti ) ti .
Необходимое условие экстремума:
a N
N
ti 0,
ln( L(t1 ,..., t N ; , a))
0
i 1
d (a)
.
ln( L(t ,..., t ; , a))
1
N
N
0
d (a)
0
a
N ln( ) ln( ti ) N
(a)
i 1
Из первого уравнения следует
a
N
1
ti
N i 1
a
.
Tˆ
После подстановки во второе уравнение
получим уравнение для получения оценки параметра a:
Или в развернутом виде:
1 N
t
d (ln( (a ))
ln( i )
ln( a ) G (a).
N i 1 T
da
d (a)
1
t
ln( i ) da ln( a) G(a).
N i 1 T
( a )
N
aˆ
Получив оценку параметра aˆ , вычисляем и оценку параметра по формуле ˆ .
Tˆ
10

11.

Метод максимального правдоподобия
для точечной оценки неизвестных параметров заданного распределения
Для распределения Вейбулла с неизвестных параметров a и b для полной выборки
a 1
a 1
t a
t a
a t
a t
F (t ) 1 exp - , f (t ) exp , (t ) ,
b
b b
b b
b
N
Функция правдоподобия
N
a
t
L(t1 ,..., t N ; a, b) i
b i 1 b
a 1
e
t
i
b
a
.
N
N
i 1
i 1
ln( L(t1 ,..., t N ; a, b)) N ln( a) N a ln( b) (a 1) ln( ti ) b a ti .
a
Необходимое условие экстремума:
ln( L(a, b))
a
a N a
N
ti 0,
b
b b a 1 i 1
ln( L(a, b)) N
N
N
N
a
a
N ln( b) ln( ti ) b a ln( b) ti b a [ti ln( ti )] 0.
a
a
i 1
i 1
i 1
1
N a a
ti
b i 1
N
Из первого уравнения находим выражение для
и, подставляя его во второе уравнение, приходим к уравнению:
N
N
N
ln( ti ) N
a i 1
t
i 1
a
i
ln( ti )
N
t
i 1
0,
a
i
которое надо разрешить относительно параметра a. После чего остается вычислить bˆ.
11

12.

Метод максимального правдоподобия
для точечной оценки неизвестных параметров заданного распределения
Расчет параметров a и b распределения Вейбулла для цензурированной выборки
Имеем усеченную выборку объемом V m s , содержащую:
• ряд наработок с отказами 1 , 2 ,..., i ,..., m;
• ряд безотказных наработок t1 , t 2 ,..., t j ,..., t s .
Функция правдоподобия
m
m
s
i 1
i 1
j 1
ln L m ln a ma ln b (a 1) ln( i ) b a ( ia t aj )
Необходимое условие экстремума:
s
L
a
a m a
m
(
t aj ) 0
i
a 1
b
b b
i 1
j 1
L m
m
m
s
m
s
m ln b ln( i ) b a ln b( ia t aj ) b a ( ia ln i t aj ln t j ) 0
a a
i 1
i 1
j 1
i 1
j 1
m
s
( ia t aj )
Из первого уравнения находим выражение для bˆ
i 1
1
a
j 1
m
и, подставляя его во второе уравнение, приходим к уравнению:
m
m
ln i m
a (i )
i 1
s
a
i
ln i t aj ln t j
j 1
m
i 1
s
a
i
t
j 1
0
a
j
которое надо разрешить относительно параметра a . После чего остается вычислить bˆ.
12

13.

Вычислительные трудности решения сложных алгебраических
уравнений при применении ММ и ММП
1. Алгебраическое уравнение для нахождения параметра а распределения Вейбулла
при применении ММ
2
1 2
2 1
D ((T ) / Г (1 )) 1 1 0,
a
а a
2. Алгебраическое уравнение для нахождения параметра aˆ Гамма-распределения
методом МП
d ( a )
N
t
1
ln( i ) da ln(a) 0.
N i 1 T
( a )
d ( a )
da ln(a) G(a).
Введем обозначение
( a )
3. Алгебраическое уравнение для нахождения параметра aˆ распределения Вейбулла
N
N
N
ln(ti ) N
a i 1
t
i 1
a
i
ln(ti )
N
t
i 1
0.
a
i
13

14.

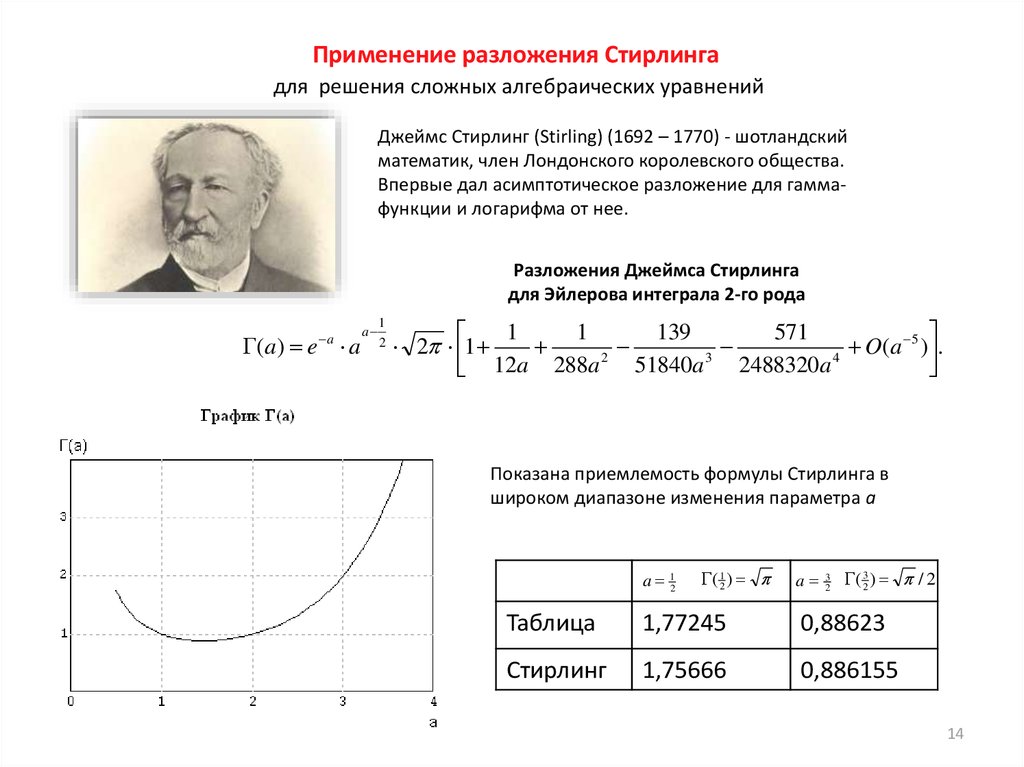
Применение разложения Стирлинга
для решения сложных алгебраических уравнений
Джеймс Стирлинг (Stirling) (1692 – 1770) - шотландский
математик, член Лондонского королевского общества.
Впервые дал асимптотическое разложение для гаммафункции и логарифма от нее.
Разложения Джеймса Стирлинга
для Эйлерова интеграла 2-го рода
a
( a ) e a
a
1
2
1
1
139
571
2 1
O(a 5 ) .
2
3
4
51840a
2488320a
12a 288a
Показана приемлемость формулы Стирлинга в
широком диапазоне изменения параметра а
a 12
( 12 )
a
3
2
( 32 ) / 2
Таблица
1,77245
0,88623
Стирлинг
1,75666
0,886155
14

15.

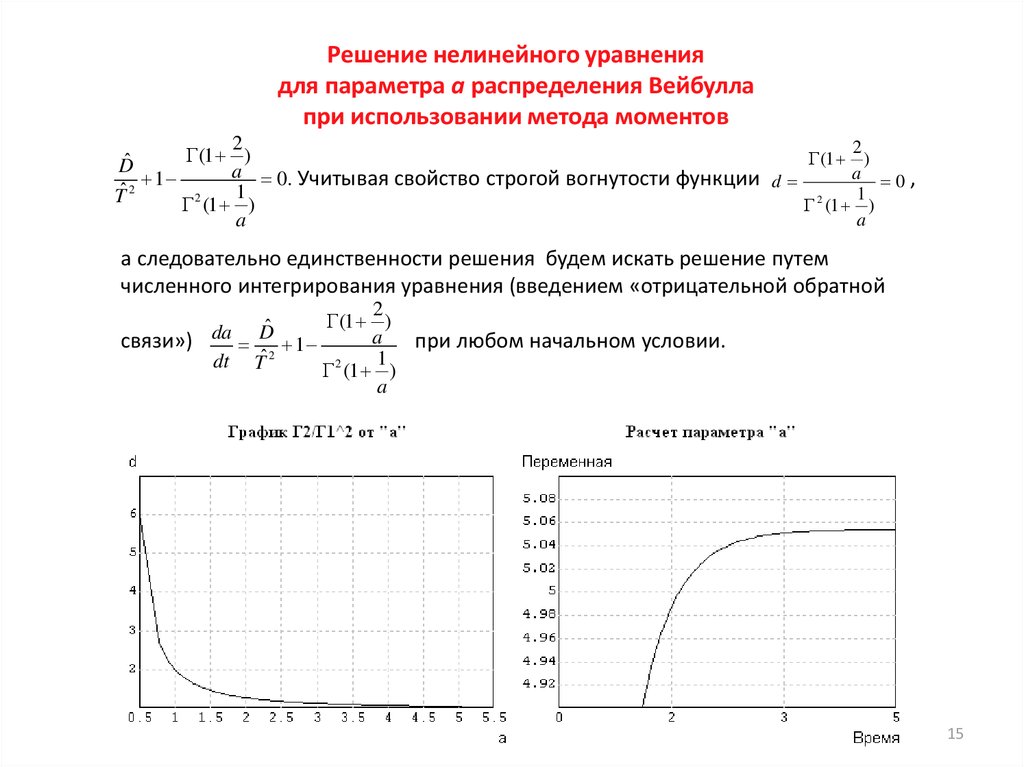
Решение нелинейного уравнения
для параметра а распределения Вейбулла
при использовании метода моментов
2
2
(1 )
(1 )
ˆ
D
a 0. Учитывая свойство строгой вогнутости функции d
a 0,
1
2
ˆ
1
1
T
2 (1 )
2 (1 )
a
a
а следовательно единственности решения будем искать решение путем
численного интегрирования уравнения (введением «отрицательной обратной
2
(1 )
ˆ
a
связи») da D 1
при любом начальном условии.
2
ˆ
1
dt T
2
(1 )
a
15

16.

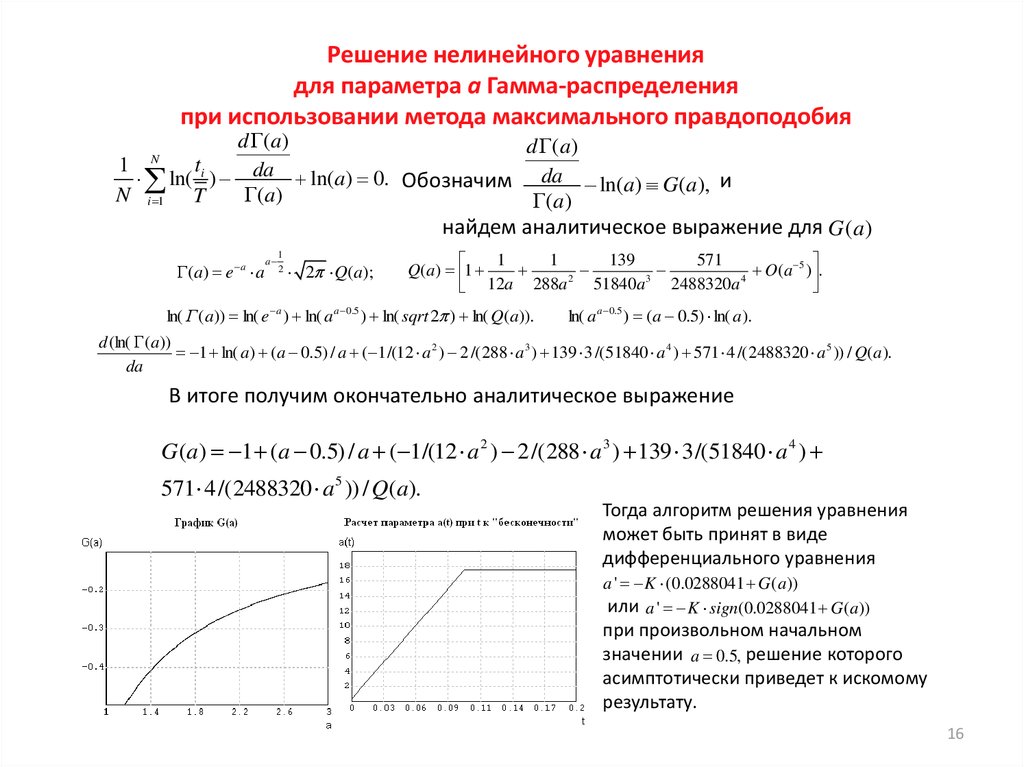
Решение нелинейного уравнения
для параметра а Гамма-распределения
при использовании метода максимального правдоподобия
d ( a )
d ( a )
ti
1
ln( ) da ln(a) 0. Обозначим da ln(a) G(a), и
N i 1 T
( a )
( a )
N
найдем аналитическое выражение для G (a )
(a) e a a
a
1
2
2 Q(a);
1
1
139
571
Q(a) 1
O(a 5 ) .
2
3
4
51840a 2488320a
12a 288a
ln( Г (a)) ln( e a ) ln( a a 0.5 ) ln( sqrt 2 ) ln( Q(a)).
ln( a a 0.5 ) (a 0.5) ln( a).
d (ln( (a))
1 ln( a) (a 0.5) / a ( 1 /(12 a 2 ) 2 /( 288 a 3 ) 139 3 /(51840 a 4 ) 571 4 /( 2488320 a 5 )) / Q(a).
da
В итоге получим окончательно аналитическое выражение
G(a) 1 (a 0.5) / a ( 1/(12 a 2 ) 2 /( 288 a 3 ) 139 3 /(51840 a 4 )
571 4 /( 2488320 a 5 )) / Q(a).
Тогда алгоритм решения уравнения
может быть принят в виде
дифференциального уравнения
a ' K (0.0288041 G (a))
или a ' K sign(0.0288041 G (a))
при произвольном начальном
значении a 0.5, решение которого
асимптотически приведет к искомому
результату.
16

17.

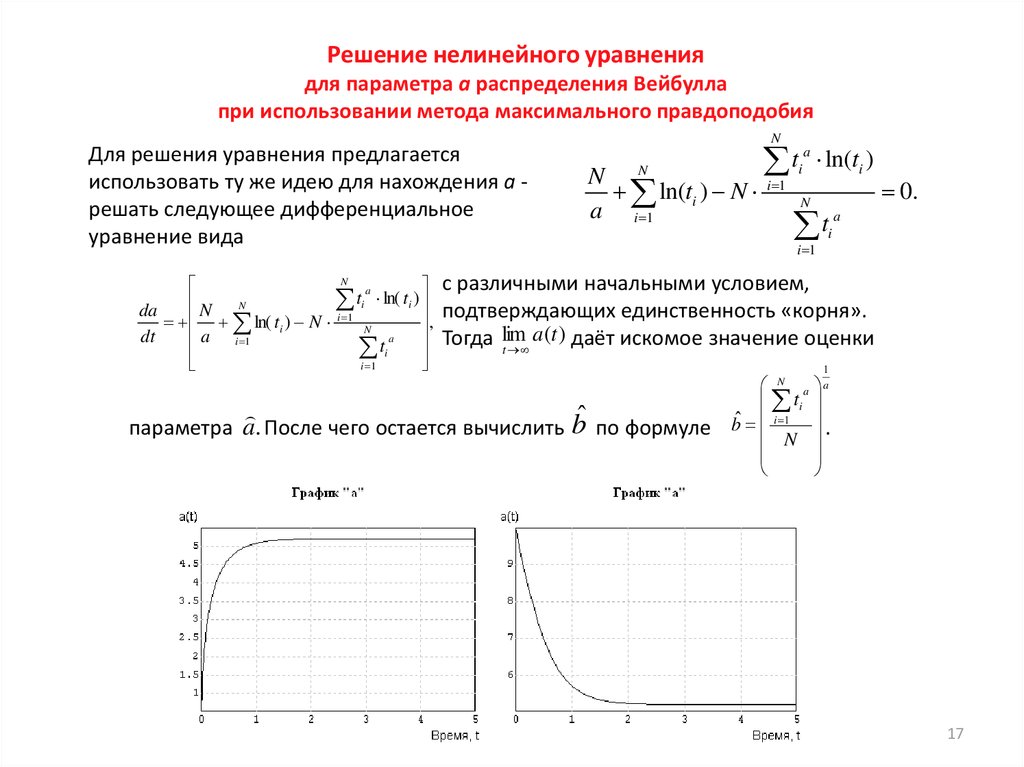
Решение нелинейного уравнения
для параметра а распределения Вейбулла
при использовании метода максимального правдоподобия
Для решения уравнения предлагается
использовать ту же идею для нахождения а решать следующее дифференциальное
уравнение вида
N
a
ti ln( ti )
N
da
N
,
ln( ti ) N i 1 N
dt
a
a i 1
ti
i 1
N
N
N
ln(ti ) N
a i 1
t
i 1
ln(ti )
N
t
i 1
0.
a
i
с различными начальными условием,
подтверждающих единственность «корня».
a (t ) даёт искомое значение оценки
Тогда lim
t
параметра a. После чего остается вычислить bˆ по формуле
1
a
a
ti
bˆ i 1 .
N
N
a
i
17

18.

Решение тестовой задачи
Распределение Вейбулла
ММ
ММП
Гамма-распределение
ММ
ММП
a = 5.054
a = 5.2061
a = 19,294
a = 17,52
b = 179.308
b = 179.232
λ = 0,121433
λ = 0.106401
18

19.

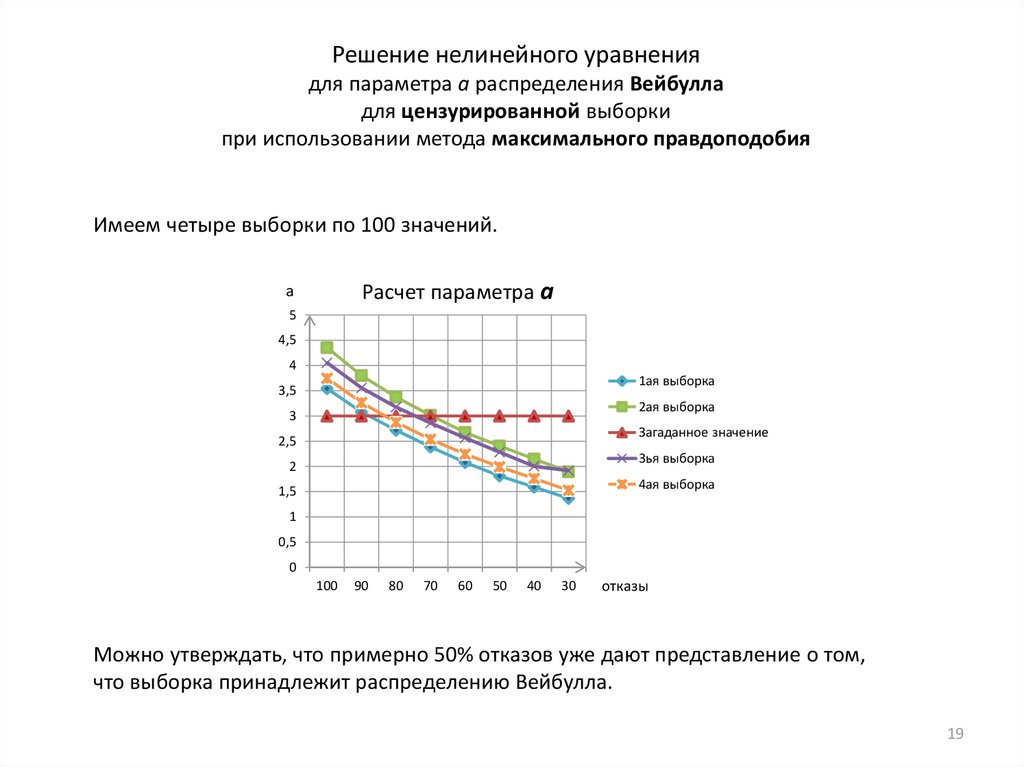
Решение нелинейного уравнения
для параметра а распределения Вейбулла
для цензурированной выборки
при использовании метода максимального правдоподобия
Имеем четыре выборки по 100 значений.
Расчет параметра a
a
5
4,5
4
1ая выборка
3,5
2ая выборка
3
Загаданное значение
2,5
3ья выборка
2
4ая выборка
1,5
1
0,5
0
100
90
80
70
60
50
40
30
отказы
Можно утверждать, что примерно 50% отказов уже дают представление о том,
что выборка принадлежит распределению Вейбулла.
19

20.

Результаты работы
1. Разработано алгоритмическое и программное обеспечение для получения точечных оценок
параметров двух практически важных распределений - распределения Вейбулла и гаммараспределения методом моментов, методом максимального правдоподобия и методом
вероятностных сеток («вероятностной бумаги»). Разработан и программно реализован
также алгоритм проверки выполнимости критерия А.Н. Колмогорова – критерия согласия
аппроксимирующего распределения эмпирическому (ступенчатому) распределению.
2. Системы расчетов полностью реализованы в среде отечественного Программного комплекса
«МВТУ 3.5».
3. Показано, что применение предложенных алгоритмов позволило исключить необходимость в
«ручном» проведении расчетов показателей надежности и в обращения к многочисленным
числовым статистическим таблицам. Все необходимые данные получаются расчетным
путем с использование соответствующих моделей и формул. По информации о первых
выборочных четырех начальных и центральных моментах и об эмпирической функции
распределения расчетным путем автоматически находятся параметры практически всех
типовых распределений, а также значения гамма-функции (эйлерова интеграла второго
рода).
Вывод
В работе сделан научно-технический задел для решения на ЭВМ перспективных задач
обработки информации с малыми или ограниченными по объему выборками, в том числе
с различными типами цензурирования, то есть усеченными выборками, методами
моментов и максимального правдоподобия, как с точечными, так и интервальными
оценками параметров предполагаемых распределений.
20

21. Критерии согласия

• Критерий согласия Колмогорова
D N max Fэм (t ) F (t ) N
t
Вер{D N x } 1
k
k
2 2
(
1
)
exp(
2
k
x )
k
• Критерий “Стареющего” распределения
1
mk
N
i N
k
t
i
k 1,2,3,4.
i 1
M k 1 M k 1 M
2
k
mk
Mk
k!

22.

Критерий согласия Колмогорова
x
D N max Fэм (t ) F (t ) N
t
Вер{D N x } 1
k
k
2 2
(
1
)
exp(
2
k
x )
k
а
0,20
0,10
0,05
0,02
0,01
0,001
х
1,073
1,224
1,358
1,520
1,625
1,950
22

23.

Очень спасибо
за внимание !
23

24.

24