Пример решения транспортной задачи (закрытая модель). Исследование операций

1.

Пример решения
транспортной задачи
(закрытая модель)
Исследование операций

2. Задача

Составить оптимальный план перевозок груза из трех
пунктов отправления с запасами 30, 48, 24 т в четыре
пункта назначения с потребностями 18, 27, 42, 15 т.
Тарифы перевозок сij (в ден/ед.) из (i= 1,2,3) в (j=l,..,4)
приведены в матрице
13 7 11 5
C 11 8 13 7
6 10 12 9

3. Рассмотрим методы построения опорных планов (опорного решения) ТЗ

4. Метод северо-западного угла

Заполняют клетку A1B1, (левый верхний угол), поставив в
него min(a1b1). Если min совпадает с A1, то запасы пункта
A1 считают исчерпанными и переходят к удовлетворению
потребностей b1 начиная с ячейки А2В1.
Затем переходят к заполнению клетки А2В2. Перемещаясь
так по диагонали, доходят до последней клетки АmВn. При
этом все грузы будут исчерпаны, и потребности пунктов
удовлетворены.
Замечание: если на некотором шаге исчерпаны запасы, то
переходим к удовлетворению потребностей как это было
описано выше. Если же были удовлетворены потребности,
то приступают к исчерпыванию запасов аналогичным
способом.

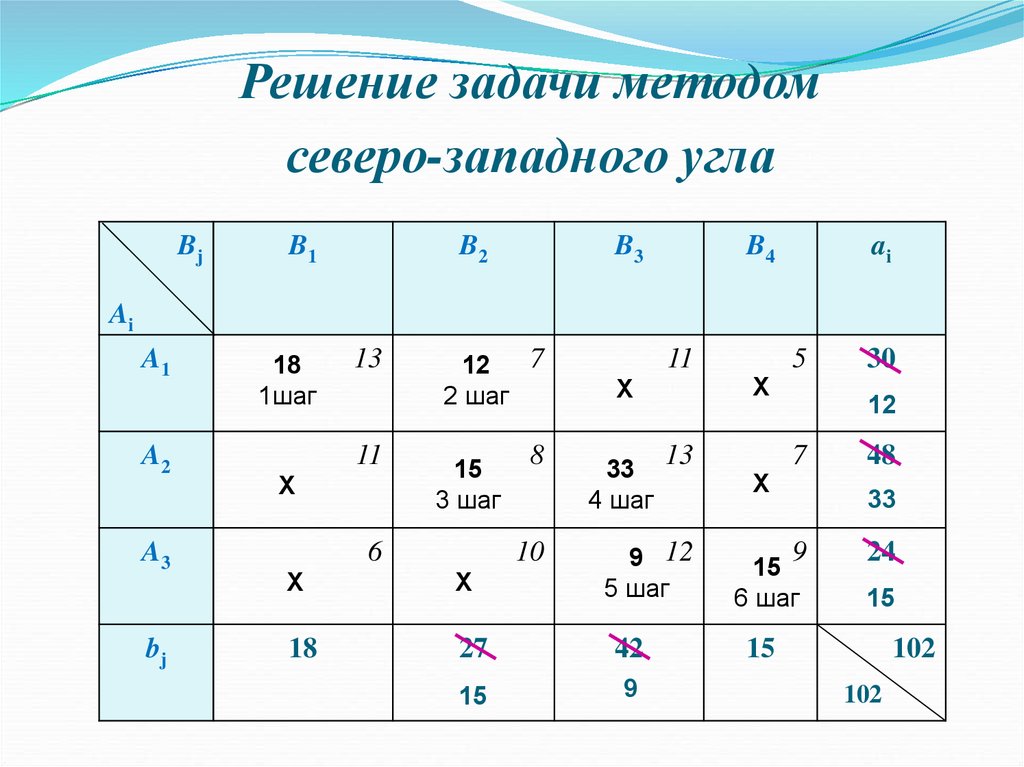
5.

Решение задачи методом
северо-западного угла
Bj
B1
B2
B3
B4
ai
Ai
A1
A2
A3
bj
18
1шаг
13
11
Х
7
12
2 шаг
15
3 шаг
6
8
10
11
Х
33
4 шаг
13
9 12
5 шаг
Х
Х
18
27
42
15
9
Х
Х
5
30
12
7
48
33
9
15
6 шаг
24
15
15
102
102

6. Опорное решение задачи

18 12 0 0
X 0 15 33 0
0 0 9 15

7. Метод аппроксимации Фогеля

1. На каждом шаге находят разности между двумя
наименьшими тарифами (даже если они одинаковые) во
всех строках и столбцах, записывая их в дополнительные
столбец и строку таблицы;
2. Из найденных разностей выбирают максимальную и
заполняют клетку, которой соответствует данная разность.
Процесс продолжается до тех пор, пока все грузы не будут
развезены по потребителям.

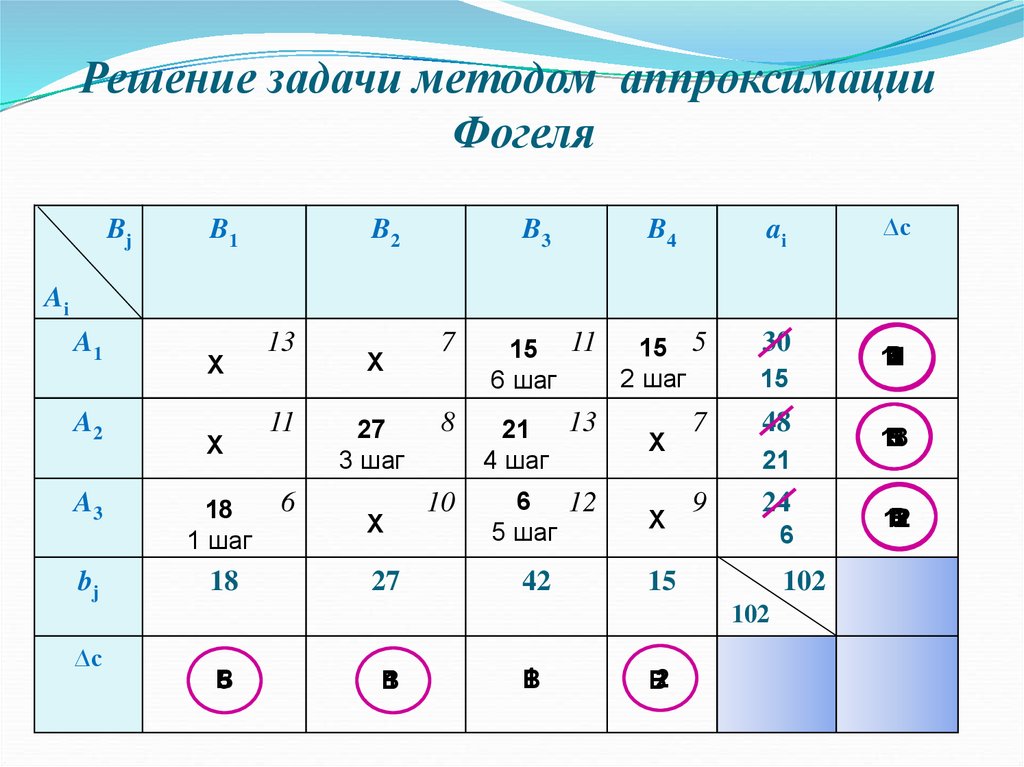
8.

Решение задачи методом аппроксимации
Фогеля
Bj
B1
B2
B3
B4
ai
∆с
30
В
11
2
4
Ai
A1
A2
A3
bj
Х
Х
18
1 шаг
18
13
11
6
Х
27
3 шаг
Х
27
7
8
10
15 5
15 11
2 шаг
6 шаг
21 13
4 шаг
Х
6 12
5 шаг
Х
42
7
15
48
21
9
24
6
15
102
102
∆с
В
5
В
1
1
В
В2
13
В
1
5
В
13
12
2

9. Опорное решение задачи

0 0 15 15
X 0 27 21 0
18 0 6 0

10. Метод минимальной стоимости для нахождения опорного плана

Предполагает заполнение на каждом шаге
клеток с минимальным тарифом, что даст,
очевидно, меньшие суммарные затраты на
перевозку груза.

11.

Решение задачи методом наименьшей
стоимости
Bj
B1
B2
B3
B4
ai
15 5
1 шаг
30
15
7
48
Ai
A1
A2
A3
bj
13
Х
11
Х
18
2 шаг
18
7
15
3 шаг
12
4 шаг
6
8
10
Х
Х
36
6 шаг
11
13
6 12
5 шаг
27
42
12
36
Х
36
9
Х
24
6
15
102
102

12. Опорное решение задачи

0 15 0 15
X 1 0 12 36 0
18 0 6 0

13. Метод потенциалов

базируется на следующей теореме
(признак оптимальности решения):
Для заполненных ячеек таблицы должно выполняться
условие: ui v j cij
Для незаполненных ячеек условие:
u v
i
j
cij
(причем количество заполненных ячеек в опорном
плане должно быть равно n+m-1, где m – число
поставщиков, n – число потребителей)

14. Проверим план, полученный с помощью метода наименьшей стоимости, на оптимальность

0 15 0 15
0 12 36 0
X1
18 0 6 0
n+m-1=4+3-1=6
Должно быть заполнено 6 ячеек.
Реально заполненных ячеек тоже 6.

15. Составим систему уравнений для заполненных ячеек:

0
X1 0
Составим систему уравнений
18
для заполненных ячеек:
13
C 11
6
Полагая u1 = 0, найдем: v2 = 7
u1 + v 2 = 7
v4 = 5
u1 + v 4 = 5
u2 + v 2 = 8
Так как v2 = 7, то u2 = 1
u2 + v3 = 13 Так как u2 = 1, то v3 = 12
Так как u3 = 0, то v1 = 6
u3 + v 1 = 6
u3 + v3 = 12 Так как v3 = 12, то u3 = 0
15
12
0
7
8
10
0
36
6
11
13
12
Итак, u1 = 0, u2 = 1, u3 = 0, v1 = 6, v2 = 7, v3 = 12, v4 = 5
15
0
0
5
7
9

16. Проверим второе условие теоремы для незаполненных ячеек

0 15 0 15
13 7 11 5
0 12 36 0 C 11 8 13 7
X1
18
0
6
0
6
10
12
9
u1 = 0, u2 = 1, u3 = 0,
v1 = 6, v2 = 7, v3 = 12, v4 = 5
u1 + v1 = 6 ≤ C11 = 13
u1 + v3 = 12 > C13 = 11
u2 + v1 = 7 ≤ C21 = 11
u2 + v4 = 6 ≤ C24 = 7
u3 + v2 = 7 ≤ C32 = 10
u3 + v4 = 5 ≤ C34 = 9
План X1 не оптимальный, поэтому необходимо
перераспределение грузов
+
( 1)
+
+
+
+

17.

Перераспределение грузов
осуществляется с помощью циклического сдвига
Цикл - ломанная, вершины которой находятся в
заполненных ячейках, кроме одной. Это одна
вершина должна находиться в незаполненной
ячейке, для которой ui + vj > Cij.
При этом звенья ломанной должны удовлетворять
следующим условиям:
1. Параллельность строкам и столбцам
2. В каждой строке и каждом столбце не более двух
вершин

18.

Построение цикла
Построим цикл:
u1 + v3 = 12 > C13 = 11
X
0 15 0 15
0 12 36 0
1
18 0 6 0
Всем вершинам ломанной припишем + или –,
начиная с проблемной ячейки:
0 15 0 15
0 12 36 0
X1
18
0
6
0

19.

0 15 0 15
0 12 36 0
Циклический сдвиг
X1
6
0
18 0
В свободную клетку помещаем груз величиной ,
равной минимальному значению из всех чисел в
отрицательных клетках цикла. Min (15,36)=15
Сдвиг по циклу: Во все положительные клетки
прибавляем , из отрицательных – вычитаем .
0 0 15 15
0 27 21 0
Новый план: X 2
18
0
6
0
Проверим новый план на оптимальность

20. Составим систему уравнений для заполненных ячеек:

0 0
X 2 0 27
Составим систему уравнений
18 0
для заполненных ячеек:
13 7
C 11 8
6 10
Полагая u1 = 0, найдем: v3 = 11
u1 + v3 = 11
u1 + v 4 = 5
u2 + v 2 = 8
u2 + v3 = 13
u3 + v 1 = 6
u3 + v3 = 12
15 15
21 0
6 0
11 5
13 7
12 9
v4 = 5
Так как u2 = 2, то v2 = 6
Так как v3 = 11, то u2 = 2
Так как u3 = 1, то v1 = 5
Так как v3 = 11, то u3 = 1
Итак, u1 = 0, u2 = 2, u3 = 1, v1 = 5, v2 = 6, v3 = 11, v4 = 5

21. Проверим второе условие теоремы для незаполненных ячеек

0 0 15 15
13 7 11 5
X 2 0 27 21 0 C 11 8 13 7
18
0
6
0
6
10
12
9
u1 = 0, u2 = 2, u3 = 1,
v1 = 5, v2 = 6, v3 = 11, v4 = 5
u1 + v1 = 5 ≤ C11 = 13
u1 + v2 = 6 ≤ C12 = 7
u2 + v1 = 7 ≤ C21 = 11
u2 + v4 = 7 ≤ C24 = 7
u3 + v2 = 7 ≤ C32 = 10
u3 + v4 = 6 ≤ C34 = 9
План X2 оптимальный
+
+
+
+
+
+

22. Оптимальное решение:

0 0 15 15
X 2 0 27 21 0
18 0 6 0
13 7 11 5
C 11 8 13 7
6 10 12 9
Zmin=15*11+15*5+27*8+21*13+18*6+6*12=909

23. Используемая литература:

Борзунова Т.Л., Барыкин М.П. , Данилов Е.А.
Соловьева О.Ю. - Математическое моделирование:
учебное пособие/ВолгГТУ, - Волгоград, 2008.
Конюховский П.В. Математические методы
исследования операций в экономике – СПб: Питер,
2000.