Similar presentations:
Определение.Модуль числа а
1. Определение
Модуль числа а или абсолютнаявеличина числа а равна а, если а
больше или равно нулю и равна –
а, если а меньше нуля:
2. Геометрическая интерпретация
|а| означает расстояние на координатнойпрямой от точки, изображающей число а, до
начала отсчета.
Если а 0, то на координатной прямой
существует две точки а и –а, равноудаленные
от нуля, модули которых равны.
Если а=0, то на координатной прямой |а|
изображается точкой 0.
3. Пример 1. Решить неравенство:
3x 2 2 x 1 2 x 1Решение.
Рассмотрим четыре случая.
1)
x 1,
x 1
x 1
3
x
2
2
x
2
2
x
1
x
1
3)
2
2
x 1,
x 1, 2 x 1
3
2) 3
4)
3
3
x
2
2
x
2
2
x
1
x
1
2
2
0 x , 1
0 x
3 x 2
3
1
3
3
3x 2 2 x 2 2 x 1 x
3
x 0,
x 0,
x 1
3x 2 2 x 2 2 x 1 x 1
Объединим эти решения:
Ответ:
1
( ; 1 ;
3
4. Пример 2. Решить уравнение:
x 2 x 5 x 2 x 9 10.Пусть x 2 x 5 . Тогда уравнение примет вид a a 4 10. . Воспользуемся
геометрическим смыслом модуля: найдем все точки числовой оси, сумма расстояний от каждой
из которых до точек 0 и 4 равна 10.
Решение.
а 3,
а а 4 10
а 7;
Ответ: {-4, -2, 1, 3}
x 1,
x 2,
x 2 x 5 3,
x 2 x 2 0,
2
2
x 4,
x x 5 7
x x 12 0
x 3.
5. Пример 3: Решить уравнение:
x x 2 2(2 x 1).2
Решение: Уравнение равносильно следующему:
x 2 4 x 2 x 2 ( x 2) 2 x 2 2 0.
Пусть t =|x-2|, t ≥ 0
. Тогда ( x 2 )2 t 2 , и уравнение примет вид: t
Но t ≥ 0, поэтому t = 1, откуда
Ответ: {1, 3}
x 1,
x 2 1
x 3.
2
t 1,
t 2 0
t 2.
6. Пример 4. Решить уравнение (неравенство):
22
а)
x 3x 20 x 3x 2 ;
б)
x 2 3x 2 3 x 2;
в)
x 3 2 x 1 x 3 1;
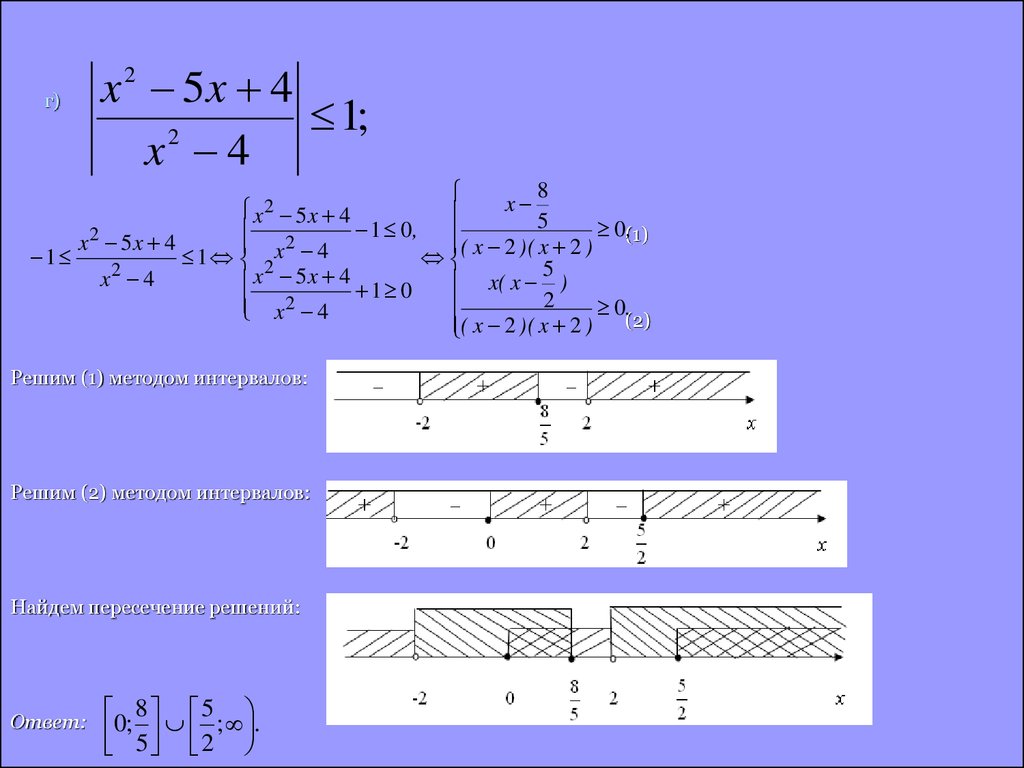
г)
x 2 5x 4
1;
2
x 4
д)
3x 2 2 x 1 2 x 2 x 1 x 2 x .
7.
Решение: а) Так как обе части неравенства неотрицательны, то возведение в квадрат являетсяравносильным преобразование:
а)
x 2 3x 20 x 2 3x 2 ;
( x 2 3x 20) 2 ( x 2 3x 2) 2 ( x 2 3x 20) 2 ( x 2 3x 2) 2 0
( x 2 3x 20 x 2 3x 2)( x 2 3x 20 x 2 3x 2) 2 0
11
(6 x 22)(2 x 18) 0 x ( x 3)( x 3) 0.
3
2
2
Решим последнее неравенство методом интервалов:
Ответ:
; 3 3; 11 .
3
8. б)
2x 3x 2 3 x 2;
2
x ,
3x 2 0,
3
x 6,
2
x 0,
x 3x 2 3x 2,
x 2.
x 2 3x 2 3x 2 x 6
x 2
Ответ: {2, 6}
9. в)
x3 2 x 1 x3 1;x 3 2 x 1 x 3 1,
x 1,
3
3
x 2 x 1 x 1 2 x( x 1)( x 1) 0.
Решим второе неравенство последней совокупности методом интервалов:
Объединяя найденные решения с решением неравенства , получим ответ.
Ответ:
( ; 1 [0;1].
10. г)
x 2 5x 41;
2
x 4
8
x
x2 5x 4
5
0,
1 0,
2
x2 5x 4
x 4
( x 2 )( x 2 ) (1)
1
1 2
2
5
x 4
x 5x 4 1 0
x 2 4
Решим (1) методом интервалов:
Решим (2) методом интервалов:
Найдем пересечение решений:
Ответ:
8 5
0; 5 2 ; .
x( x )
2
0.
( x 2 )( x 2 ) (2)
11. д)
3x 2 2 x 1 2 x 2 x 1 x 2 x .Перепишем уравнение (так как |-a|=|a|):
3x 2 2 x 1 2 x 2 x 1 x 2 x
Из свойства 10:
a b a b ab 0
Тогда уравнение равносильно неравенству:
(3 x 2 2 x 1) ( 2 x 2 x 1) 0
(3 x 2 2 x 1) (2 x 2 x 1) 0
1
1
2
x
x
x
1
0.
2
3
Метод интервалов дает:
Ответ:
1 1
2 ; 3 1
12. Ответы для самоконтроля
1. а) x 0 ; б) x 0 ; в) x 0 ; г) x 0 ; д) x 0 ; е) x 0 . 2. а) ;0 2; ; б) ; 2 0;2 ;в) ;0 ( 1; ); г) ;1 2;3 . 3. а) 2;8 ; б) 12;2 ; в) 4;0 ; г) 1 ; д) ; 15 1; ;
;3
3
е) 2;4 ; ж) ; 4 ( 1; ) ; з) 3,5;1,5 ; и) 4;5 ; к) ; 1,5 3,5; ; л) 1;1 ; м) ; 2 ( 1; );
н) 5; 1 ; о) ;4 ; п)
4 ; р) 3; 1;2;4 ; с) 3; 1 2;4 . 4. а) 2 4 ; б) ;1 5; ;
2
;
;
3
5 3
в) 2;2 ; г) 1; . 5. а) 1;1 ; б) ; 7 5;5 7; ; в) 0;6 ; г) 2; 1 1;0 2;3 3;4 .
6. а) 1;1 ; б) 2 ; в) 3;1;3;9 ; г) 1 ; д) 4;18 ; е) 2 ; ж) 3 1 ; з) 1 ; и) 3 3 ;
;4
8 ; 2
1; 5 2 ;
;1
;0;1
3
5
3
2
4 3 ; о)
6
5
к) ; 1 (1; ) ; л) ;1 (1; ) ; м) ;0 1; ; н)
; п) 1 ; 2 2
2 3
; ;
; ( ; )
3 2
5
7







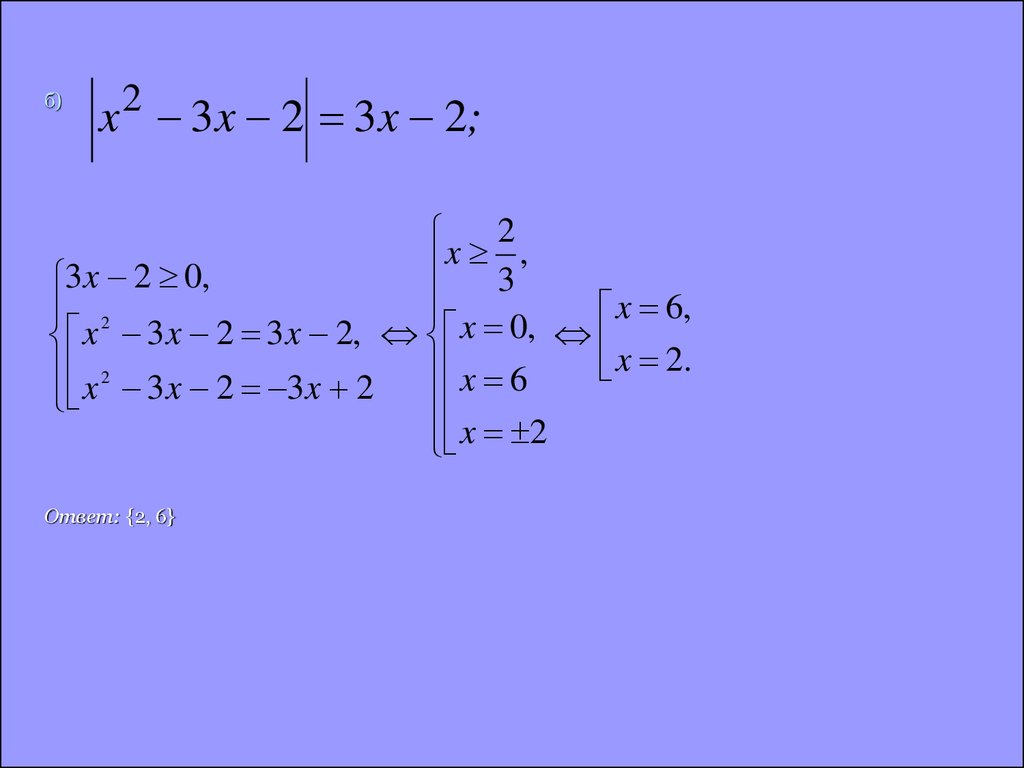



 mathematics
mathematics








