Особенности условий автоматического регулирования и управления ЭПС

1.

Лекция 2
1. Особенности условий автоматического регулирования и управления ЭПС.
2. Технико-экономическая эффективность автоматизации процесса управления ЭПС.
3. Функциональные элементы САР ЭПС: задающие, промежуточные, датчики, объекты
регулирования.
1
На работу систем автоматического управления ЭПС оказывают существенное
влияние следующие факторы.
Высокий уровень возмущений, воздействующих на ЭПС и особенно на системы автоматики. К таким детерминированным возмущениям относятся: изменения нагрузки,
нестабильность питающего напряжения, нестабильность температур, воздействие
вибраций и динамических импульсов, электромагнитные помехи.
Разнообразие принципов оптимизации режимов тяги и торможения ЭПС.
Принцип наиболее полного использования мощности оборудования. Для электрооборудования его можно сформулировать в общем виде, как
τмакс(Т)→kзττдоп,
где τмакс(Т) – максимальное превышение температуры над температурой окружающей
среды в пределах рассматриваемого цикла работы Т; τдоп – допустимое превышение
температуры для данного вида оборудования; kзτ < 1 – коэффициент запаса по превышению температуры.
Принцип минимального расхода энергии при выполнении заданного графика движения.
При этом должно выполняться условие
T
T
n
п
0
0
Aм A ( 1 / T ) U cidt ( U c / Tn ) idt ; Tп Tпз

2.

где А и Ам – соответственно выполненный и минимальный расход энергии; Тпз и Тп –
соответственно заданное и действительное время хода по перегону.
Этот принцип применяют наиболее часто.
Принцип реализации максимальной пропускной способности участка (наибольшей
скорости). Он может быть сформулирован как
L
dl
Tп мин Tп
v
0
где Тп мин – минимальное время движения на перегоне: L – длина перегона.
Один из вариантов этого принципа – регулирование заданной постоянной ходовой
скорости vх:
vi → vх = kз vvмакс =const,
где vмакс – максимальная допустимая скорость (конструкционная скорость подвижного состава); kз v<1 – коэффициент запаса по скорости.
Принцип полного использования эксплуатационных ограничений. Он предусматривает
выбор режимов работы на границе допустимых предельных значеv 4
А
ний (ограничений) показателей процессов в условиях эксплуата3
Б
ции. К ним относятся ограничения по перегрузочной способности
В
различных элементов оборудования, например, тяговых двигатеГ
лей (прямая 1 на рис. 11), по сцеплению (кривая 2), по потенциаль2
ной устойчивости – коммутации (кривая 3) и по предельной скорости vмакс (прямая 4).
1
Работе локомотива при использовании этого принципа оптиFк
мизации соответствует на рис. 11 тонкая линия А.
Рис. 11

3.

Комбинированный принцип оптимизации. Он заключает в совмещении нескольких
принципов, отмеченных ранее. Например, принцип постоянства скорости или принцип минимального расхода энергии может быть совмещен с принципом использования ограничений в различные моменты движения. Работе локомотива при совмещении принципа постоянства скорости с принципом использования ограничений соответствуют тонкие линии Б,
В, Г (см. рис. 11). По-видимому, комбинированные принципы оптимизации наиболее универсальны и приемлемы в общих случаях.
Синхронизация работы САР ЭПС необходима при работе ЭПС по системе многих
единиц. Отсутствие синхронизации может вызывать недопустимые перегрузки элементов
оборудования отдельных локомотивов и другие неблагоприятные явления.
Рассмотрим проявления технико-экономической эффективности при различ1
ных уровнях автоматизации ЭПС:
1. Автоматическое управление в режиме тяги позволяет улучшить тяговые свойства
локомотива: плавное регулирование силы тяги взамен ступенчатого позволяет увеличить
расчетный коэффициент сцепления на 5…8 %.
2. Автоматизация управления торможением дает возможность повысить скорость движения поезда за счёт большей точности управления, а электрическое торможение – снизить
расход электроэнергии и износ тормозных колодок. Без автоматического регулирования
невозможно функционирование рекуперативного торможения на переменном токе.
3. Автоматизация вспомогательных устройств локомотива позволяет снизить расход электроэнергии на вспомогательные нужды, использовать более компактные и надежные устройства.
4. Эффективность автоведения поездов проявляется в увеличении провозной и улучшении
использования пропускной способности участков и сопровождается уменьшением расхода
электроэнергии на тягу поездов за счёт выбора оптимальных режимов движения.

4.

5. На некотором уровне автоматизации возможно сокращение состава локомотивной бригады. При сопряженном автоматическом телеуправлении поездами возможно существенно
снизить трудовые затраты персонала, обслуживающего управление движением (диспетчеры движения и др.), системы тягового электроснабжения и т.д.
6. Автоматизация управления ЭПС благодаря снижению возмущений, воздействующих на
основные его подсистемы даёт возможность повысить ремонтопригодность, снизить
удельную ремонтоёмкость и затраты на техническое обслуживание.
3
Функциональная схема системы автоматики представляет собой её графическое
изображение, подразделяющее рассматриваемую систему на элементы, выполняющие типовые функции. Элементом называют конструктивно обособленную часть автоматической системы, выполняющую определенные функции.
Элементы различают по принципам действия (электромеханические, электромашинные, электромагнитные, пневматические, полупроводниковые, электронные и т. п.), по
исполнению (общепромышленные, тяговые и т.п.), по конструкции, а также по функциональному назначению.
В зависимости от назначения различают следующие элементы:
– задающий элемент (задатчик), с помощью которого в САР вводят сигнал g,
пропорциональный заданному значению регулируемой величины у;
– программный элемент, обеспечивающий изменение задаваемого значения g*
регулируемой величины у по установленной программе;
– чувствительный элемент, предназначенный для ввода в САР сигнала z,
пропорционального текущему значению регулируемой вели чины у, а также сигналов qi*,
характеризующих уровень возмущений q;
– элемент сравнения, выполняющий сравнение сигналов, пропорциональных заданному

5.

и текущему значению регулируемой величины, для выявления ошибки или рассогласования Δ=g – z;
– управляющий элемент, формирующий управляющее воздействие х в зависимости от
значения рассогласования Δ или от сигнала qi*, пропорционального возмущению;
– исполнительный элемент, осуществляющий регулирующее воздействие μ на объект
регулирования;
– промежуточный элемент, выполняющий необходимое промежуточное преобразование сигнала.
Совокупность чувствительного, управляющего, исполнительного и промежуточных
элементов, а также элемента сравнения представляет собой автоматический регулятор
(АР).
Ввиду большого разнообразия промежуточных элементов их подразделяют дополнительно на усилительные, преобразовательные, логические и вычислительные.
Сравним упрощенную схему управления автоматическим пуском электропоезда (рис.
12а) и соответствующую ей функциональную схему (рис. 12б). Функции исполнительного
элемента ИЭ выполняет реостатный контроллер РК, коммутирующий ступени пускового
реостата Rп секции вторичной обмотки тягового трансформатора или реостата ослабления
возбуждения, а также изменяющий группировки тяговых двигателей ТД, которые являются объектом регулирования ОР. Роль задающего элемента ЗЭ1 выполняет пружина ВП реле ускорения РУ, с помощью которой регулируется уставка наименьшего значения пускового тока Iм.
Чувствительным элементом ЧЭ является силовая катушка С реле ускорения, а элементом сравнения – якорь Я магнитопровода М, к которому приложены сила возвратной пружины Рвп и электромагнитная сила Рэ зависящая от суммы магнитодвижущих сил (м.д.с.)
Fнс и Fнп силовой С и подъемной П катушек.

6.

а)
б)
в)
Рис. 12
Преобразование м.д.с. в электромагнитную силу Рэ, происходит в магнитной
системе РУ. На схеме, приведенной на рис. 12б, этому соответствует промежуточный
элемент ПЭ1.
После окончания перехода на очередную реостатную позицию ток i в силовой
катуш-ке по мере увеличения скорости уменьшается, и когда он становится равным Iм
якорь Я реле ускорения под действием разности сил ΔР отпадает и замыкает контакты 1РУ
цепи питания привода РК. Эти контакты следует рассматривать как промежуточный
элемент ПЭ2, имеющий характеристику, приведенную на рис. 12в. При подаче напряжения
пита-ния и привод РК переключает реостатный контроллер на следующую позицию, в
резуль-тате чего ток двигателя скачком возрастает, и якорь Я притягивается к
магнитопроводу М, размыкая контакты 1РУ.
Машинист имеет возможность задавать с помощью контроллера КМ (задающий

7.

мент ЗЭ2) позицию привода исполнительного элемента РК, на которой должен закончиться процесс пуска. Кроме того, машинист может изменять значение Iм, меняя напряжение
питания катушки П с помощью кнопочного выключателя ПУ (задающий элемент ЗЭ3). Изменение уставки происходит также при буксовании, когда реле буксования РБ замыкает
свой контакт в цепи катушки П.
В общем случае объектом регулирования в системах автоматизации ЭПС является поезд, а конечной регулируемой величиной – параметры, характеризующие его перемещение, т.е. скорость v, путь l или время хода t.
Однако в ряде частных случаев регулируемой величиной может быть сила тяги или ток
тяговых двигателей. Поэтому целесообразно в общем случае рассмотреть объект регулирования в виде функциональной цепочки, в которой первые два блока соответствуют электромагнитным процессам в тяговом двигателе, а другие два блока – механическим процессам в тяговой передаче и собственно в поезде как в механической системе (рис. 13а).
Вначале целесообразно рассмоа)
треть только электромагнитные
WF=WЭМWМ
ик
процессы (блок Wi), описываемые
i
МЭ
Fк
β
Wi
WЭМ
WМ
Wv
дифференциальными уравнениями
ив
в схеме замещения двигателя, содержащей только сосредоточенiв
v
ные элементы (активное сопротивб)
в)
г)
д)
ление r, индуктивность l, источник
– ЭДС).
ик
i
i
и
i
и
i
к
в
Wпi-uк
Wпi-β
Wнi-uк
Wнi-uв
Т.К. скорость протекания электромагнитных процессов на поряРис. 13
док выше скорости протекания

8.

механических, то электромагнитные процессы можно рассматривать при неизменной скорости поезда v = const.
Если рассматривать тяговый двигатель последовательного возбуждения с электромагнитным моментом Мэ и силой тяги Fк, то для него возможны два способа регулирования,
когда входной величиной являются соответственно напряжение питания ик (рис. 13б) или
коэффициент регулирования м.д.с. β (рис. 13в).
Для двигателя независимого возбуждения тоже имеются два способа регуа)
в)
лирования: по напряжению питания
якорной обмотки ик (рис. 13г) и по напряжению питания обмотки возбуждения ив (рис. рис. 13д).
г)
Тяговый двигатель последовательного возбуждения, регулируемый по
б)
напряжению (рис. 14а) может быть
описан нелинейным дифференциальным уравнением
д)
d
ri uê å,
dt
где ψ – потокосцепление; r – сопротивление обмоток двигателя; ик – приРис. 14
ложенное к двигателю напряжение; е –
ЭДС.
При этом ψ‚ может быть условно представлено как ψ =Li=wвФ где wв – количество витков
обмотки возбуждения.

9.

Индуктивность двигателя L сильно зависит от тока, а ЭДС определяется выражением
е=сеФv, где величина сеФ представляет собой существенно нелинейную характеристику.
Таким образом, L и е являются нелинейными функциями тока. На рис. 14б и в показан характерный вид функции сеФ(i) и L(i). Исходное нелинейное выражение целесообразно записать в виде
d
dt
( Li) ri uê ceÔ v,
где выражение в скобках следует продифференцировать как произведение двух переменных, в результате чего получим
dL di
L
i
ri uê ceÔ v.
di dt
В этом уравнении выражение в скобках представляет собой эквивалентную индуктивность нелинейной схемы замещения Lэ, которая может быть вычислена по характеристике
L(i) (рис. 14в) при помощи производной dL/di (рис. 14г). Характерная зависимость Lэ(i)
приведена на рис. 14д.
Расчеты процессов регулирования с учетом нелинейностей сводятся к решению полученного уравнения методом малых отклонений заключающегося в том, что в качестве исходного рассматривается стационарное состояние системы, характеризующееся неизменными параметрами v0, Uк0, I0 и Ф т.е.
rI0=Uк0 – сеФv.
Далее задаются малым отклонением входной величины Δик(t), которое вызывает отклонение выходной величины Δi(t) (рис. 15а). При этом в окрестности выбранной базовой
точки имеем Lэ0≈const, а зависимость магнитного потока (или ЭДС) от тока считают лиdÔ
нейной, т.е.
Ô Ô i
Ô ê i.
0
di
0
Ô

10.

поскольку
то
v 0 è e0 e ce (Ô 0 êÔ i ),
d
Lýî ( I 0 i) r ( I 0 i) (U ê0 è ê ) ce (Ô 0 êÔ i)v0 .
dt
Вычитая из этого уравнения приведенное ранее уравнение стационарного режима для
базовой точки и учитывая, что d
d
( I 0 i)
i,
dt
dt
получим
d
Lýî i r i è ê ce êÔ iv0
dt
или в операторной форме
( Lýî p r i ceê Ô v0 ) i ( p) è ê ( p),
что позволяет записать передаточную функцию в виде
Wi ï uê
êiï uê
i ( p)
W1 ( p)
,
ï
uê ( p )
1 W1 ( p)W2 ( p)W3 ( p) 1 Òi uê ð
б)
а)
Δик
Wпi-uк
Δi
WпFк-i
ΔFк
Δик-Δе
Δе
W1=1/(Lp+r)
W3=сеv0
Рис. 15
ΔФ
W2=кФ
Δi
где
кiп uк 1 /( r ceкФv )
и
Ti ï uê Lý0 / (r ceêÔ v).
Структурная схема двигателя, соответствующая передаточной функции, приведена на рис. 15б.

11.

Двигатель последовательного возбуждения с регулированием м.д.с. (рис. 16а) описывается уравнением в отклонениях
Lýî
d
( I 0 8i ) rý ( I 0 i ) U ê0 è ê ce (Ô 0 êÔ i )v0 ,
dt
где rэ=βrв+rя – эквивалентное сопротивление двигателя при регулировании м.д.с.
Поскольку β=βо+Δβ, то rэ=(βо+Δβ)rв+rя. Приращение тока возбуждения iв=βi можно
выразить по формуле полного дифференциала в виде
Δiв=Δiβ+ΔβI0.
б)
а)
i
W8=cмI0
М
Δик
n
Δβ
ик
L
Δi в
W3=кФ
W1=I0
iв=βi
ΔФ
W4=cev0
i
-
W5=1/(Lэp+β0r+rя)
Δiв
W7=cмФ0
-
W2=rв
W6=β0
в)
г)
W3W6W8
Δuк
Δβ
W1
ΔФ
W3W4
W2
-
W5
Δi
W7
ΔFк
-
Δик
Δβ
W3W4W6
W3W8
Рис. 16
Wпi-uк
Δi
Wпi-β
WпFк-i
ΔFк
ΔFк

12.

Подставляя выражения для rэ и Δiв в уравнение и пренебрегая величинами второго порядка малости типа ΔiΔβ или Δi2 получим окончательно:
d i
Lýî
I 0râ β β0râ i rÿ i è ê ceêÔ v0 (β0 i I 0 β),
dt
что после применения операционного метода дает возможность составить структурную
схему (рис. 16б).
Преобразовав эту схему по известным правилам, к виду, показанному на рис. 16в и г,
найдём передаточные функции тягового двигателя по регулирующему воздействию Δβ(р),
т.е.
W ( p)
Wi ï W1 ( p)[W2 ( p) W3 ( p)W4 ( p)]
I0
Wi ï uê
5
1 W3 ( p)W4 ( p)W5 ( p)W6 ( p)
râ ce êÔ v0
;
Lý p 0 râ rÿ ce êÔ 0v0
W5 ( p)
1
.
1 W3 ( p)W4 ( p)W5 ( p)W6 ( p) Lý p 0râ rÿ ceêÔ 0v0
Эти передаточные функции соответствуют апериодическим звеньям 1-го порядка.
Двигатель независимого возбуждения, регулируемый по напряжению на якорной
обмотке (рис. 17а и б), описывается уравнением в отклонениях
d i
Lÿý
rÿ i è ê e,
dt
которое соответствует уравнению двигателя последовательного возбуждения для случая
Ф=const и v=const. Из этого уравнения получим передаточную функцию в виде, соответст-

13.

а)
i
М
ик
вующем инерционному звену 1-го порядка, т. е.
iв
Wi í uê
L ив=const
n
Δик
Wнi-uк
Δi
WнFк-i
в)
Δик
Wi нuк
Δiв
Δi
WнFк-i
ΔFк
а)
ив
d iÿ
rÿ iÿ è ê ce êÔ v0 iâ ;
dt
d i
Lâý â râ iâ è â .
dt
ик=const
М
Δик
в)
L
Δβ
n
Wпi-uк
Δi
Wпi-β
WпFк-i
ΔFк
Δив
W6=ceI0
Δик
б)
W1=1/(Lвр+rв)
p 1
Lÿý
Рис. 17
iв
T
,
Структурные схемы двигателя даны на рис. 17в и г.
В двигателе независимого возбуждения, регулируемого по цепи возбуждения (рис. 18а), процессы описываются системой уравнений в отклонениях:
ΔFк
г)
1
Lя rя
í
i uê
êií uê 1/ rÿ ; Òií uê Lÿý / rÿ.
при этом
б)
Δе
êií uê
Δiв
W2=кФ
W3=cev0
Δе
Рис.18
W4=1/(Lяр+rя)
Δi
W5=смФ0
ΔFк
Структурная схема
для этого варианта
(рис. 18б) может
быть преобразована
к виду, приведённому на рис. 18в, а передаточные функции
по регулирующему и
возмущающему воз-

14.

действиям определяются выражениями:
í
i uâ
W
êií uâ
êií uê
ce êÔ v0
í
W1 ( p )W2 ( p)W4 ( p)]
; Wi uê ( p)
,
( Lâ p râ ) ( Lÿ p rÿ ) (Ò1 p 1)(T2 p 1)
Ò2 p 1
где êií uâ
ce êÔ v0
1
L
L
, êií uê , T1 âý , Ò2 ÿý .
rÿrâ
rÿ
râ
rÿ
При дальнейшем анализе структурной цепочки (см. рис. 6.2а) целесообразно объединить элементы Wэм(р) и Wм(р) и рассматривать сразу преобразование тока i в силу тяги Fк в
соответствии с выражением
Fк=смФi,
где см – электромеханическая постоянная.
Для базовой точки
Fк0=смФ0I0.
С учетом малого отклонения входной величины
Fк0 +ΔFк =см (Ф0 +ΔФ) (I0+Δi).
Преобразуем это уравнение к виду
Fк0 +ΔFк =см (Ф0 +кФΔi) (I0+Δi)
Вычитая из последнего уравнения уравнение стационарного режима для базовой точки, получим
ΔFк =см (Ф0Δi + кФI0Δi +кФΔi2)
Слагаемым с Δi2 можно пренебречь как величиной второго порядка малости. Тогда
окончательно получим
ΔFк =см(Ф0 + кФI0)Δi,
что дает передаточную функцию в виде

15.

ï
Fê i
W
Δi
п
W
ΔFк
Fк-i=кFк
Рис. 19
F ( p)
cì (Ô 0 êÔ I 0 ) ê Fê ,
i ( p)
ê
т.е. для выбранной базовой точки передаточная функция представляет постоянный коэффициент (рис. 19).
Для двигателя последовательного возбуждения с регулированием м.д.с. (рис. 16) на
изменения Fк будут влиять как изменения тока i, так и изменения магнитного потока Ф,
поэтому выражение для ΔFк может быть выражено в операторной форме
F ( p) W7 ( p) i( p) W8 ( p) Ô(p), W7 ( p) cì Ô 0 , W8 ( p) cì I 0
ê
Для определения передаточной функции воспользуемся преобразованиями структурной схемы, приведенными на рис. 16, из которых
W ( p)W8 ( p)[1 W3 ( p )W4 ( p )W5 ( p)W6 ( p)]
WFê i ( p) W7 ( p) W3 ( p)W6 ( p)W8 ( p) 3
[W2 ( p) W3 ( p)W4 ( p)]W5 ( p)
ê I ( L p 0 râ rÿ ce ê Ô 0v0 )
cì Ô 0 Ô 0 ý
.
râ ce êÔ v0
Для тягового двигателя независимого возбуждения, регулируемого по напряжению
(рис. 17а), при постоянном магнитном потоке имеет место пропорциональная зависимость Fк =см Ф0i, так что
W í ( p) c Ô ,
Fê i
ì
0
т.е. передаточная функция соответствует постоянному коэффициенту как это показано на
рис. 17г.
Для двигателя независимого возбуждения, у которого входной величиной является на-

16.

пряжение на обмотке возбуждения Δив (рис. 18а), преобразование ΔФ и Δi в ΔFк аналогично
рассмотренному на рис. 16в. Перенося, как и в том случае, точку разветвления с выхода
звена W2(р) на выход W4(р), получим передаточную функцию для рассматриваемого варианта:
WFê i ( p) W5 ( p)
W6 ( p)
I
cì Ô 0 0 ( Lÿ ð rÿ )] .
W3 ( p)W4 ( p)
cev0
Последний элемент в схеме объекта регулирования Wv (см. рис. 15а) реализует преобразование, описываемое уравнением движения поезда
dv
1
dt 1
Fê
(
w
w
)
0
ä ,
m
где т – масса поезда; w0 – основное удельное сопротивление движению; wд –
дополни-тельное сопротивление от уклонов и кривых.
Уравнение движения в малых отклонениях имеет вид
d
1 Fк
v
w
w
0
д
dt
1 m
Поскольку w0= а0 + а1v + а2v2, то Δw0 = (а1 + 2а2v0)Δv. С учётом этого уравнение в отклонениях примет вид:
d
1 Fк
v
(
a
2
a
v
)
v
w
1
2 0
д
dt
1 m
или в операторной форме записи

17.

1 Fê ( p)
p v
(
a
2
a
v
)
v
(
p
)
w
(
p
)
,
1
2 0
ä
1 m
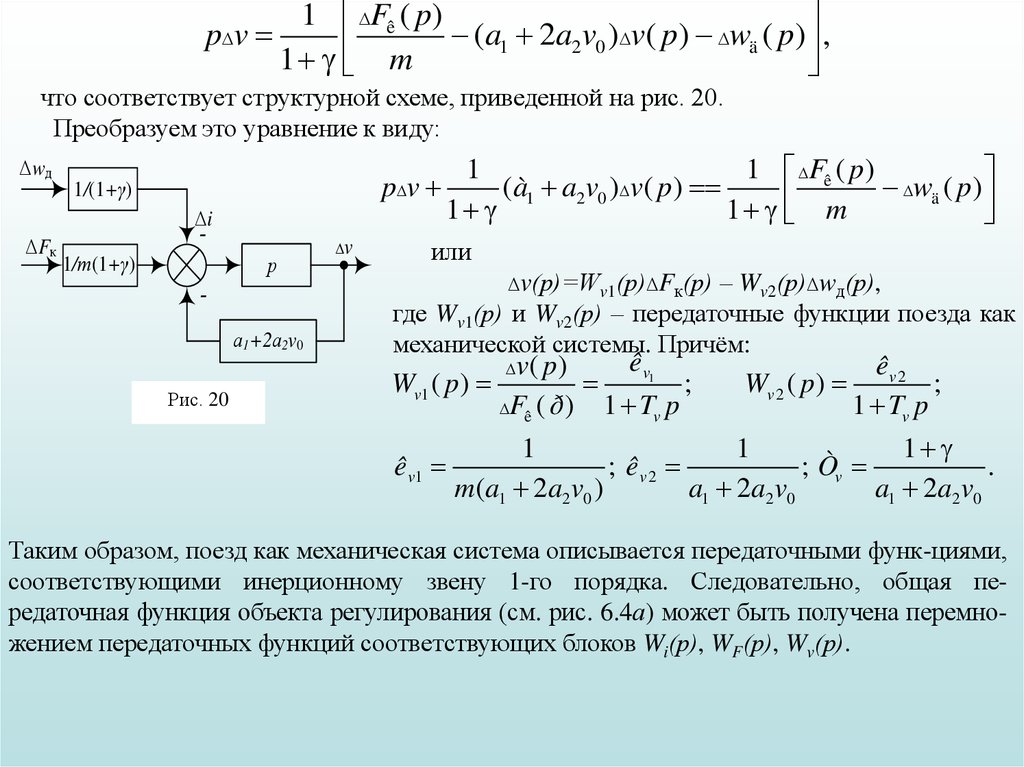
что соответствует структурной схеме, приведенной на рис. 20.
Преобразуем это уравнение к виду:
Δwд
p v
1/(1+γ)
Δi
ΔFк
-
р
1/т(1+γ)
а1+2а2v0
Рис. 20
Δv
1
1 Fê ( p)
(à1 a2v0 ) v( p)
wä ( p )
1
1 m
или
Δv(р)=Wv1(р)ΔFк(р)
– Wv2(р)Δwд(р),
где Wv1(р) и Wv2(р) – передаточные функции поезда как
механической системы. Причём:
Wv1 ( p )
ê v1
ê v1
v( p)
;
Fê ( ð )
1 Tv p
Wv 2 ( p )
êv 2
;
1 Tv p
1
1
1
; êv 2
; Òv
.
m(a1 2a2v0 )
a1 2a2v0
a1 2a2v0
Таким образом, поезд как механическая система описывается передаточными функ-циями,
соответствующими инерционному звену 1-го порядка. Следовательно, общая передаточная функция объекта регулирования (см. рис. 6.4а) может быть получена перемножением передаточных функций соответствующих блоков Wi(р), WF(р), Wv(р).