ViS_8_klass_24_urok

1.

2.

XI.
Математические рассуждения важная тема в математическом
образовании - как в исследованиях,
так и на практике. Согласно
Кембриджскому
словарю
английского языка, рассуждение это «процесс размышления о чем-то
с целью принятия решения».

3.

XI.
Основными понятиями логики
рассуждений
являются
высказывания и логические связки
(операции над высказываниями “и”
и “или”).

4.

49

5.

Логическими утверждениями являются утвердительные
предложения, о которых можно судить, истинны они или
ложны. Причем они не могут быть истинными и ложными
одновременно. Логика высказываний рассматривает эти
предложения не с точки зрения их смысла, содержания, а
только с точки зрения их истинности или ложности.

6.

Рассмотрим два математических утверждения: “5 больше,
чем 2” и “5 больше, чем 7”. Какое из них является
истинным, а какое ложным?
Эти два высказывания можно соединить
союзом
“и”.
Получится
сложное
утверждение “5 больше, чем 2” и “5
больше, чем 7”. Истинно оно или ложно?

7.

Чтобы сложное утверждение
“A и B” было истинным,
нужно, чтобы обе части этого
утверждения были истинны.
Логический союз “и” не зря
так называется. Его действие
очень похоже на работу союза
“и” в русском языке.

8.

3
Между двумя утверждениями можно поставить союз
“или”. Получится сложное утверждение “5 больше, чем 2”
или “5 больше, чем 7”. Как вы думаете, истинно оно или
ложно?
Оно истинно, потому что истинна
первая часть, а союз “или” не требует,
чтобы были истинны обе части: достаточно
одной.

9.

Чтобы сложное утверждение
“A или B” было истинным,
нужно, чтобы хотя бы одна
часть этого утверждения была
истинны.
Поясним слова “хотя бы одна”.
Оно значит, что утверждение “A
или
B”
будет
истинным
высказыванием, если истинным
является только утверждение A,
только утверждение B или оба
сразу.

10.

Собака Шарик, живущая в будке возле дома, обязательно
лает, если какая-нибудь кошка идёт по забору. Выберите
утверждения, которые следуют из приведённых данных.
1) Если Шарик лает, значит,по забору идёт кошка.
2) Если Шарик молчит, значит, кошка по забору не идёт.
3) Если кошка по забору не идёт, Шарик не лает.
4) Если по забору пойдёт белая кошка, Шарик будет лаять.

11.

Когда учитель физики Николай Дмитриевич ведёт урок, он
обязательно отключает свой телефон. Выберите утверждения,
которые верны при приведённом условии.
1) Если телефон Николая Дмитриевича включён, значит, он не
ведёт урок.
2) Если телефон Николая Дмитриевича включён, значит, он ведёт
урок.
3) Если Николай Дмитриевич проводит на уроке лабораторную
работу по физике, значит, его телефон выключен.
4) Если Николай Дмитриевич ведёт урок физики, значит, его
телефон включён.

12.

Согласно градостроительным нормам, в домах выше 5 этажей
должен быть установлен лифт. Выберите утверждения,
которые непосредственно из этого следуют.
1) Если в доме нет лифта, то в этом доме больше 6 этажей.
2) Если в доме больше 7 этажей, то в нём есть лифт.
3) Если в доме лифта нет, то в этом доме меньше 6 этажей.
4) Если в доме больше 8 этажей, то в нём нет лифта.

13.

50

14.

Когда люди о чем-то спорят,
одни из них считают некоторое
утверждение
истинным,
а
другие - ложным. Так, в течение
многих веков ученые спорили о
том,
истинно
или
ложно
утверждение “Солнце вращается
вокруг Земли”.

15.

Ещё несколько веков назад
все были уверены, что это
утверждение истинно, притом
совершенно очевидно (“видно
очами”). И потребовалось не
одно столетие, чтобы доказать
гипотезу Николая Коперника
(1473 - 1543), отрицающую эту,
казалось
бы,
“очевидное”
утверждение.

16.

Вообще, при споре двух людей
один из них утверждает, что
высказывание истинно, а другой
отрицает его мнение, он имеет
противоположное мнение.

17.

Рассмотрим утверждение “Сегодня на небе ясно и дует
ветерок”. Чтобы оно стало истинным высказыванием,
должны быть выполнены оба условия: и про небо, и про
ветер. Как сформулировать отрицание?
Достаточно “отменить” только ясное
небо или только ветер (можно отменить
всё сразу).

18.

Если хотя бы одна из частей сложного утверждения с
союзом “и” станет ложной, ложным станет всё утверждение.
Поэтому отрицание будет выглядеть так:
“(сегодня небо не ясное) или (нет ветра)”.
К
каждой
из
частей
сложного
утверждения мы добавили отрицание, а союз
“и” заменили союзом “или”. Получили
отрицание сложного утверждения.

19.

Отрицанием к утверждению
“A и B” является утверждение
“(не A) или (не B)”.

20.

Сформулируйте отрицание утверждения T: “В треугольнике
ABC есть прямой угол и два угла равны между собой”.
Равнобедренный
треугольник.
Для
утверждение T.
прямоугольный
него
истинно

21.

Сначала запишем утверждение T более формально:
“(в треугольнике ABC есть прямой угол)
и
(в треугольнике ABC два угла равны между собой)”.
Построим отрицание:
“(в треугольнике ABC нет прямого углп)
или
(в треугольнике ABC никакие два угла не равны)”.

22.

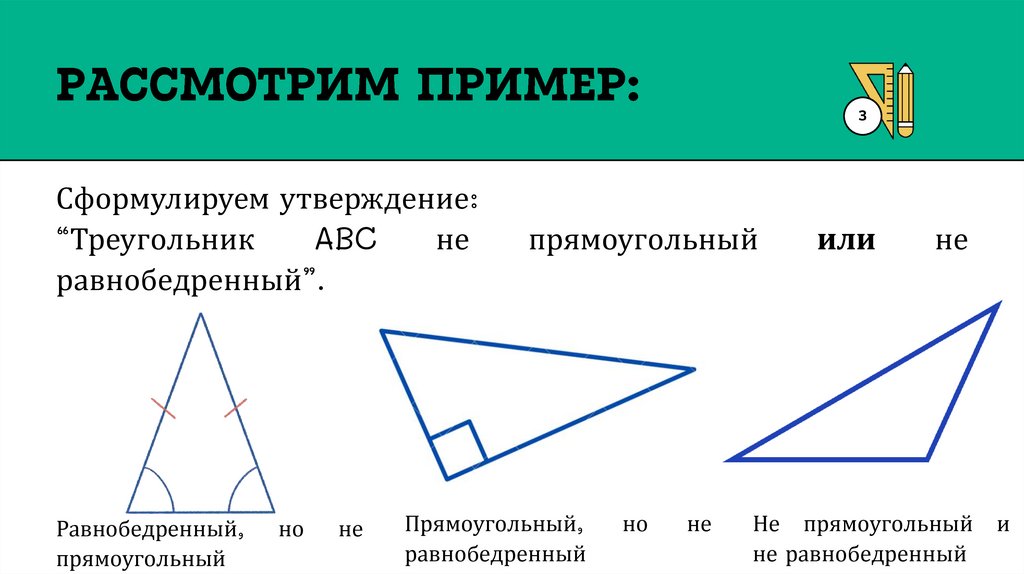
3
Сформулируем утверждение:
“Треугольник
ABC
не
равнобедренный”.
Равнобедренный,
прямоугольный
но
не
прямоугольный
Прямоугольный,
равнобедренный
но
не
или
не
Не прямоугольный
не равнобедренный
и

23.

Осталось научиться строить
отрицания
к
сложным
утверждениям с союзом “или”.
Ситуация здесь аналогичная.
Нужно построить отрицания к
обеим
частям
и
заменить
логический союз “или” союзом
“и”.

24.

3
Утверждение гласит: “Две любые прямые на плоскости
пересекаются или параллельны”. Это утверждение истинно.
Сформулируйте отрицание.
На плоскости найдутся две прямые,
которые
не
пересекаются
и
не
параллельны.

25.

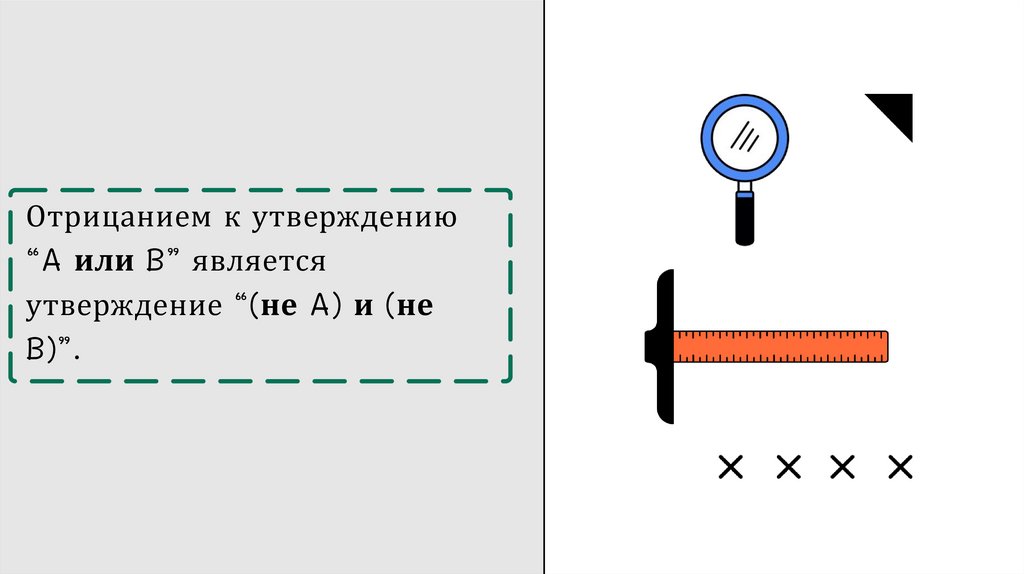
Отрицанием к утверждению
“A или B” является
утверждение “(не A) и (не
B)”.

26.

Постройте отрицание к утверждению:
а) “При бросании игрального кубика выпало менее пяти, но
более трёх очков”.
“При бросании игрального кубика выпало не менее пяти
или не более трёх очков”.
б) “При бросании игрального кубика выпало менее пяти или
более трёх очков”.
“При бросании игрального кубика выпало не менее пяти и
не более трёх очков”.

27.

Постройте отрицание к утверждению:
в) “В данном треугольнике два угла равны и в нём нет двух
равных сторон”.
“В данном треугольнике нет равных углов или в нём две
стороны равны”.
б) “В данном треугольнике два угла равны или в нём нет
двух равных сторон”.
“В данном треугольнике нет равных углов и в нём две
стороны равны”.

28.

Постройте отрицание к утверждению:
в) “Натуральное число при делении на 3 даёт остаток 1 или
2”.
“Натуральное число при делении на 3 не даёт остаток 1 и
2”.
б) “Натуральное число делится на 3 и сумма его цифр тоже
делится на 3”.
“Натуральное число не делится на 3 или сумма его цифр
тоже не делится на 3”.

29.

49, 50,