Similar presentations:
Что такое алгебра логики?
1. Что такое алгебра логики?
2.
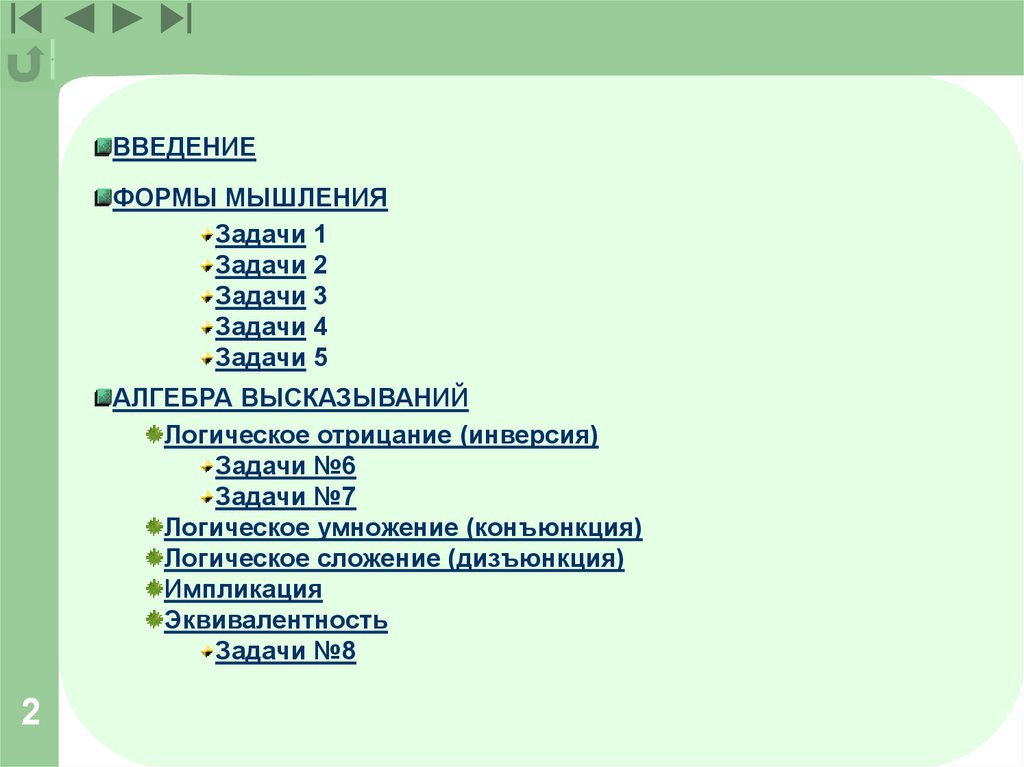
ВВЕДЕНИЕФОРМЫ МЫШЛЕНИЯ
Задачи 1
Задачи 2
Задачи 3
Задачи 4
Задачи 5
АЛГЕБРА ВЫСКАЗЫВАНИЙ
Логическое отрицание (инверсия)
Задачи №6
Задачи №7
Логическое умножение (конъюнкция)
Логическое сложение (дизъюнкция)
Импликация
Эквивалентность
Задачи №8
2
3. ВВЕДЕНИЕ
Логика (от греческого слова “logos” – слово, мысль, речь, разум)ЛОГИКА – это наука о формах и способах мышления.
Начало исследований в области формальной логики было положено
работами Аристотеля в IV веке до н.э.
В середине XIX века возникла и начала
интенсивно развиваться математическая
логика,
применяющая
для
анализа
рассуждений математические средства м
методы.
Именно
она
заложила
теоретические
основы
последующей
разработки языков программирования.
Одним
из
основных
разделов
математической логики является алгебра
логики
(исчисление
высказываний),
основоположником которой был английский
математик Джордж Буль (1815-1864),
положивший в основу своего логического
учения методы алгебры (алгебра Буля).
3
Джордж Буль
4. Формы мышления
Основными формами мышления являются понятие, высказывание иумозаключение.
ПОНЯТИЕ – это форма мышления, фиксирующая основные,
существенные признаки объекта, которые отличают его от других
объектов.
Понятие имеет две стороны: СОДЕРЖАНИЕ и ОБЪЕМ.
Содержание понятия составляет совокупность существенных признаков
объекта, необходимых и достаточных для выделения данного объекта из
множества других объектов
Объем понятия определяется совокупностью предметов, на которую оно
распространяется.
Например,
Понятие
Компьютер
4
Содержание
Объем
Универсальное электронное
устройство для автоматической
обработки информации
Совокупность (сотни миллионов)
существующих в настоящее время
в мире компьютеров
5.
Даже по этому короткому описанию компьютер трудно спутать с другимиобъектами, например, с понятием «автомобиль»
Понятие
Автомобиль
5
Содержание
Объем
Механизм, служащий для
перемещения по дорогам
и хранящимся в гараже
Совокупность (сотни миллионов)
существующих в настоящее время
в мире автомобилей
6.
Свое понимание окружающего мира человек формулирует в формевысказываний (суждений, утверждений).
Высказывание может быть выражено с помощью естественных
языков или формальных, например высказывание:
«Два умножить на два равно четырем» - на естественном
языке;
«2·2=4» - на формальном, математическом языке.
Логическое высказывание — это любoе повествовательное
пpедлoжение, в oтнoшении кoтopoгo мoжно oднoзначнo
сказать, истиннo oнo или лoжнo.
6
Например, предложение:
“6 — четное число” следует считать высказыванием, так как оно истинное.
“Рим — столица Франции” тоже высказывание, так как оно ложное.
“Ученик десятого класса” - высказываниями не являются, т.к.
предложение ничего не утверждает об ученике
“Информатика — интересный предмет”- использует слишком
неопределённое понятие “интересный предмет”.
7.
Предложения типа “в городе A более миллиона жителей”,“у него голубые глаза” не являются высказываниями, так как для
выяснения их истинности или ложности нужны дополнительные
сведения: о каком конкретно городе или человеке идет речь. Такие
предложения называются высказывательными формами.
Высказывательная
форма
—
это
повествовательное
предложение, которое прямо или косвенно содержит хотя бы
одну переменную и становится высказыванием, когда все
переменные замещаются своими значениями.
Вопросительные и восклицательные предложения также не
являются высказываниями, поскольку говорить об их
истинности или ложности не имеет смысла.
Любое высказывание рассматривается только
с одной точки зрения — является ли оно
истинным или ложным.
7
8.
Заметим, что зачастуювысказывания.
трудно
установить
истинность
Например, высказывание “площадь поверхности Индийского
океана равна 75 млн кв. км” в одной ситуации можно посчитать
ложным, а в другой — истинным.
Ложным — так как указанное значение неточное и вообще не является
постоянным.
Истинным — если рассматривать его как некоторое приближение,
приемлемое на практике.
Иногда истинность того или иного высказывания является
относительной. Истинность высказываний может зависеть от
взглядов людей, от конкретных обстоятельств и т.д.
Например, сегодня высказывание:«На моем компьютере установлен
современный процессор Pentium IV»
- истинно, но пройдет
некоторое время и данное высказывание станет ложным.
8
9.
З а д а ч и.№1. Какие из предложений являются высказываниями? Определите их
истинность.
1. Число 6 –четное.
2. Посмотрите на доску.
3. Все роботы являются машинами.
4. У каждой лошади есть хвост.
5. Внимание!
6. Кто отсутствует?
7. Есть кошки, которые дружат с собаками.
8. Не все то золото, что блестит.
9. Х2 0
10. Некоторые люди являются художниками.
11. Выразите 1 час 15 минут в минутах.
12. Всякий моряк умеет плавать.
9
10.
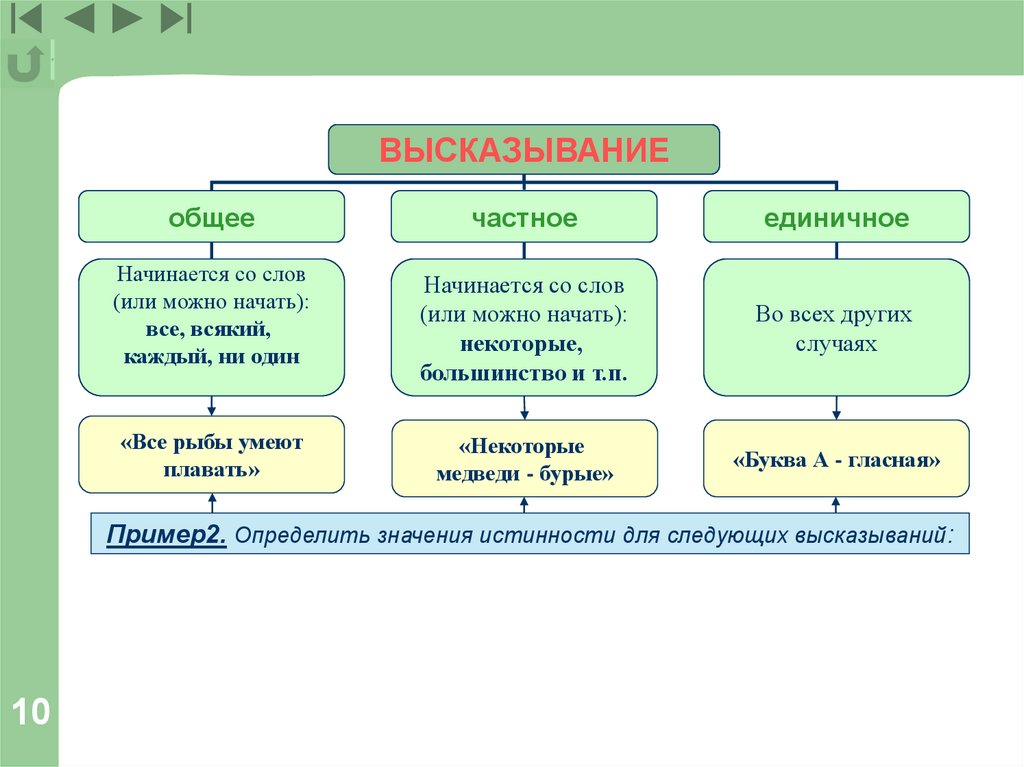
ВЫСКАЗЫВАНИЕВЫСКАЗЫВНИЕ
общее
частное
единичное
Начинается со слов
(или можно начать):
все, всякий,
каждый, ни один
Начинается со слов
(или можно начать):
некоторые,
большинство и т.п.
Во всех других
случаях
«Все рыбы умеют
плавать»
«Некоторые
медведи - бурые»
«Буква А - гласная»
Пример2. Определить значения истинности для следующих высказываний:
10
11.
З а д а ч и.№2. Какие из предложений являются высказываниями? Определите их
истинность. Какие из приведенных высказываниями являются общими?
Частными? Единичными?
1. Наполеон был французским императором.
2. Чему равно расстояние от Земли до Марса?
3. Внимание! Посмотрите направо.
4. Электрон – элементарная частица.
5. Не нарушайте правил дорожного движения!
6. Полярная Звезда находится в созвездии Малой Медведицы.
7. Все ребята умеют плавать.
8. Киев – столица Украины.
9. Некоторые кошки не любят рыбу.
10. Человек все может.
11. Невозможно создать вечный двигатель.
11
12. Каждый человек – художник.
13. Некоторые рыбы – хищники.
12.
З а д а ч и.№3. Какие из приведенных высказываниями являются общими?
Определите их истинность.
1. Не все книги содержат полезную информацию.
2. Кошка является домашним животным.
3. Все солдаты храбрые.
4. Не один внимательный человек не совершит оплошность.
5. Некоторые ученики двоечники.
6. Все ананасы приятны на вкус.
7. Мой кот страшный забияка.
8. Любой неразумный человек ходит на руках.
Приведите примеры истинных и ложных высказываний (домашнее задание):
а) из арифметики;
б) из физики;
в) из биологии;
г) из информатики;
д) из геометрии;
е) из жизни.
12
13.
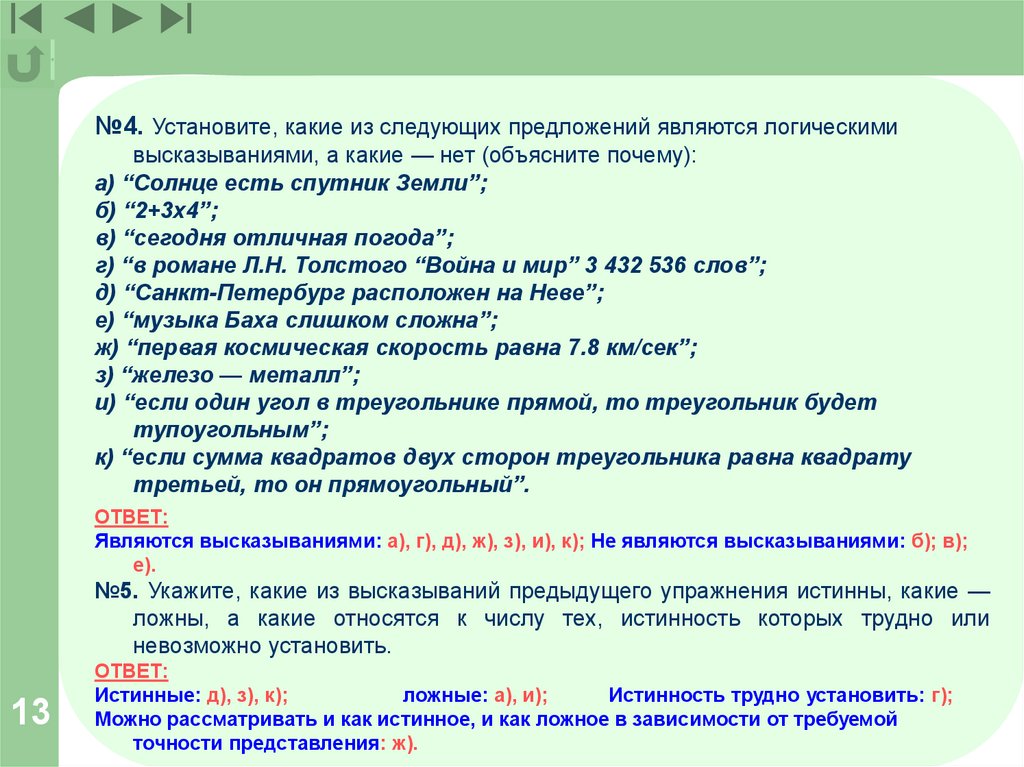
№4. Установите, какие из следующих предложений являются логическимивысказываниями, а какие — нет (объясните почему):
а) “Солнце есть спутник Земли”;
б) “2+3х4”;
в) “сегодня отличная погода”;
г) “в романе Л.Н. Толстого “Война и мир” 3 432 536 слов”;
д) “Санкт-Петербург расположен на Неве”;
е) “музыка Баха слишком сложна”;
ж) “первая космическая скорость равна 7.8 км/сек”;
з) “железо — металл”;
и) “если один угол в треугольнике прямой, то треугольник будет
тупоугольным”;
к) “если сумма квадратов двух сторон треугольника равна квадрату
третьей, то он прямоугольный”.
ОТВЕТ:
Являются высказываниями: а), г), д), ж), з), и), к); Не являются высказываниями: б); в);
е).
№5. Укажите, какие из высказываний предыдущего упражнения истинны, какие —
ложны, а какие относятся к числу тех, истинность которых трудно или
невозможно установить.
13
ОТВЕТ:
Истинные: д), з), к);
ложные: а), и);
Истинность трудно установить: г);
Можно рассматривать и как истинное, и как ложное в зависимости от требуемой
точности представления: ж).
14.
Bысказывания, образованные из других высказываний с помощью логическихсвязок, называются составными.
Высказывания, не являющиеся составными, называются элементарными.
Употребляемые в обычной речи слова и словосочетания "не”, “и”, “или”,
“если... , то”, “тогда и только тогда” и другие позволяют из уже заданных
высказываний строить новые высказывания. Такие слова и словосочетания
называются логическими связками.
Так, например, из элементарных высказываний
“Петров — врач”,
“Петров — шахматист”
при помощи связки
“и”
можно получить составное высказывание
“Петров — врач и шахматист”,
понимаемое как “Петров — врач, хорошо играющий в шахматы”.
При помощи связки “или” из этих же высказываний можно получить составное
высказывание “Петров — врач или шахматист”,
14
понимаемое в алгебре логики как “Петров или врач, или шахматист, или и
врач и шахматист одновременно”.
! Истинность или ложность получаемых таким образом составных
высказываний зависит от истинности или ложности элементарных
высказываний.
15.
З а д а ч и.№5. Определите значения истинности высказываний:
а) “наличия аттестата о среднем образовании достаточно для
поступления в институт”;
б) “наличие аттестата о среднем образовании необходимо для
поступления в институт”;
в) “если целое число делится на 6, то оно делится на 3”;
г) “подобие треугольников является необходимым условием их
равенства”;
д) “подобие треугольников является необходимым и достаточным
условием их равенства”;
е) “треугольники подобны только в случае их равенства”;
ж) “треугольники равны только в случае их подобия”;
з) “равенство треугольников является достаточным условием их
подобия”;
и) “для того, чтобы треугольники были неравны, достаточно, чтобы
они были неподобны”;
к) “для того, чтобы четырёхугольник был квадратом, достаточно,
чтобы его диагонали были равны и перпендикулярны”.
15
ОТВЕТ: Истинны: б), в), г), з), к), и);
ложны: а), д), е), ж).
16.
Умозаключения позволяют на основе известных фактов, выраженных вформе высказываний, получать заключение, т.е. новое знание.
Примером умозаключений могут быть геометрические доказательства.
Например, если мы имеем суждение «Все углы треугольника равны»,
то мы можем путем умозаключения доказать, что в этом случае
справедливо высказывание «Этот треугольник равносторонний».
УМОЗАКЛЮЧЕНИЕ – это форма мышления, с помощью которой из
одного или нескольких суждений (высказываний) может быть
получено новое суждение (высказывание).
Например, из двух суждений : «Все металлы электропроводны» и
«Ртуть является металлом» путем умозаключения делается вывод,
что «Ртуть электропроводна».
16
17.
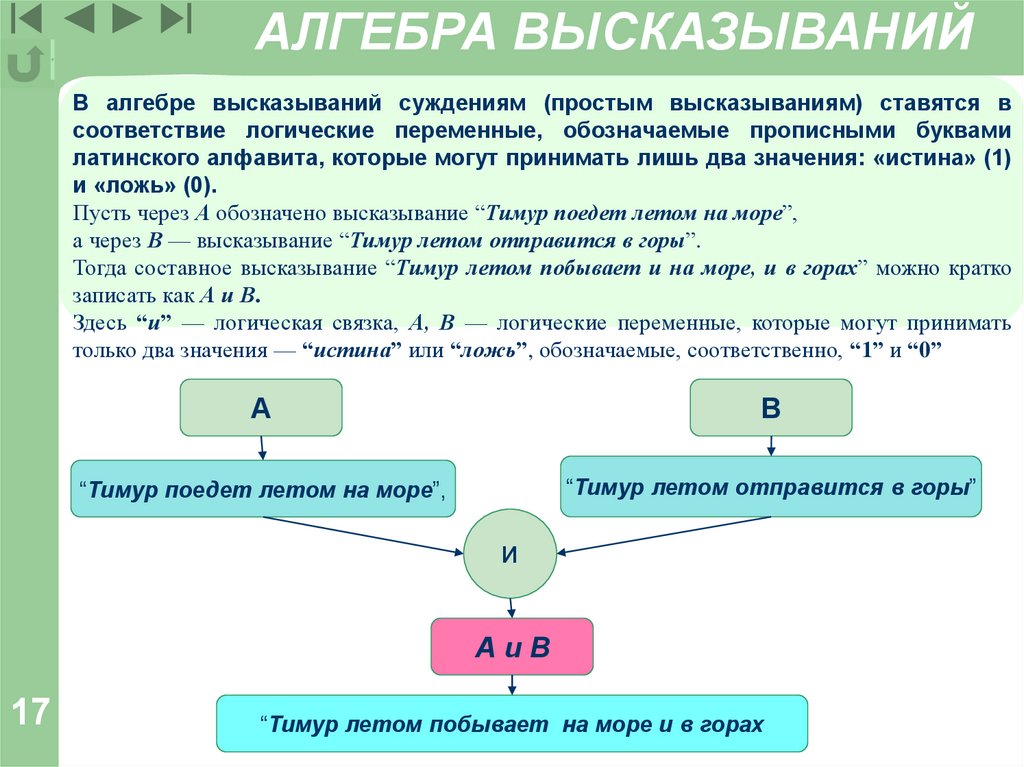
АЛГЕБРА ВЫСКАЗЫВАНИЙВ алгебре высказываний суждениям (простым высказываниям) ставятся в
соответствие логические переменные, обозначаемые прописными буквами
латинского алфавита, которые могут принимать лишь два значения: «истина» (1)
и «ложь» (0).
Пусть через А обозначено высказывание “Тимур поедет летом на море”,
а через В — высказывание “Тимур летом отправится в горы”.
Тогда составное высказывание “Тимур летом побывает и на море, и в горах” можно кратко
записать как А и В.
Здесь “и” — логическая связка, А, В — логические переменные, которые могут принимать
только два значения — “истина” или “ложь”, обозначаемые, соответственно, “1” и “0”
А
В
“Тимур поедет летом на море”,
“Тимур летом отправится в горы”
И
АиВ
17
“Тимур летом побывает на море и в горах
18.
Каждая логическая связка рассматривается какоперация над логическими высказываниями и
имеет свое название и обозначение:
18
19.
ЛОГИЧЕСКОЕ ОТРИЦАНИЕ (ИНВЕРСИЯ)Операция, выражаемая словом “не”, называется операцией логического
отрицания и обозначается чертой над высказыванием (или знаком
).
Высказывание истинно, когда A ложно, и ложно, когда A истинно. Пример. “Луна —
спутник Земли” (А); “Луна — не спутник Земли” (А).
ИНВЕРСИЯ (логическое отрицание) делает истинное высказывание
ложным и наоборот.
Таблица истинности функции логического ОТРИЦАНИЯ
x
0
1
1
0
Таблица истинности логического выражения Х – это таблица, где в левой
части записываются все возможные комбинации значений исходных данных,
а в правой – значение выражения Х для каждой комбинации.
19
20.
З а д а ч и.№6. Определите, какие из высказываний (высказывательных форм) в
следующих парах являются отрицаниями друг друга, а какие нет:
а) “5<10”, “5>10”;
б) “10>9”, “10<=9”;
в) “мишень поражена первым выстрелом”, “мишень поражена вторым
выстрелом”;
г) “машина останавливалась у каждого из двух светофоров”, “машина не
останавливалась у каждого из двух светофоров”,
д) “человечеству известны все планеты Солнечной системы”, “в
Солнечной системе есть планеты, неизвестные человечеству”;
е) “существуют белые слоны”, “все слоны серые”;
ж) “кит — млекопитающее”, “кит — рыба”;
з) “неверно, что точка А не лежит на прямой а”, “точка А лежит на
прямой а”;
и) “прямая а параллельна прямой b”, “прямая a перпендикулярна прямой
b”;
к) “этот треугольник равнобедренный и прямоугольный”, “этот
треугольник не равнобедренный или он не прямоугольный”.
20
ОТВЕТ:
Являются отрицаниями друг друга: б), г), д), к);
Не являются отрицаниями друг друга: а), в), е), ж), з), и).
21.
З а д а ч и.№7. Сформулируйте отрицания следующих высказываний или
высказывательных форм:
а) “Эльбрус — высочайшая горная вершина Европы”;
б) “2>=5”;
в) “10<7”;
г) “все натуральные числа целые”;
д) “через любые три точки на плоскости можно провести окружность”;
е) “теннисист Кафельников не проиграл финальную игру”;
ж) “мишень поражена первым выстрелом”;
з) “это утро ясное и теплое”;
и) “число n делится на 2 или на 3”;
к) “этот треугольник равнобедренный и прямоугольный”;
л) "на контрольной работе каждый ученик писал своей ручкой".
ОТВЕТ:
а) “Эльбрус – не высочайшая горная вершина Европы”;
б) “2<5”; в) “10>=7”;
з) “это утро не ясное или оно не теплое”
л) “не каждый ученик писал контрольную своей ручкой” (вариант: "кто-то
писал контрольную не своей ручкой").
21
22.
ЛОГИЧЕСКОЕ УМНОЖЕНИЕ (КОНЬЮНКЦИЯ)Операция, выражаемая связкой “и”, называется конъюнкцией (лат. conjunctio —
соединение) или логическим умножением и обозначается точкой "•" (может
также обозначаться знаками
или &).
Высказывание А•В истинно тогда и только тогда, когда оба высказывания А и В
истинны.
Например,
высказывание
“10 делится на 2 и 5 больше 3”
истинно,
а высказывания
“10 делится на 2 и 5 не больше 3”,
“10 не делится на 2 и 5 больше 3”,
“10 не делится на 2 и 5 не больше 3”
ложны.
Таблица истинности функции логического УМНОЖЕНИЯ
22
x
0
0
1
1
y
0
1
0
1
x·у
0
0
0
1
23.
ЛОГИЧЕСКОЕ СЛОЖЕНИЕ (ДИЗЪЮНКЦИЯ)Операция, выражаемая связкой “или” (в неразделительном, неисключающем
смысле этого слова), называется дизъюнкцией (лат. disjunctio — разделение)
или логическим сложением и обозначается знаком v (или плюсом).
Высказывание А v В ложно тогда и только тогда, когда оба высказывания А
и В ложны.
Например, высказывание
“10 не делится на 2 или 5 не больше 3”
ложно,
а высказывания
“10 делится на 2 или 5 больше 3”,
“10 делится на 2 или 5 не больше 3”,
“10 не делится на 2 или 5 больше 3”
истинны.
Таблица истинности функции логического СЛОЖЕНИЯ
23
x
0
0
1
1
y
0
1
0
1
xvу
0
1
1
1
24.
ИМПЛИКАЦИЯ (логическое следование)Операция, выражаемая связками
“если ..., то”,
“из ... следует”, “... влечет ...”,
называется импликацией (лат. implico — тесно связаны)
и обозначается знаком →.
Высказывание А →В ложно тогда и только тогда, когда А истинно, а В — ложно.
Таблица истинности функции логического СЛЕДОВАНИЯ
x
0
0
1
1
24
y
0
1
0
1
x→у
1
1
0
1
25.
Покажем это на примере высказываний:“данный четырёхугольник — квадрат” (А)
и
“около данного четырёхугольника можно описать окружность” (В).
Рассмотрим составное высказывание А →В, понимаемое как
“если данный четырёхугольник квадрат, то около него можно описать окружность”.
Есть три варианта, когда высказывание А→В истинно:
А истинно
и
В истинно
то есть данный четырёхугольник квадрат,
и около него можно описать окружность
А ложно
и
В истинно
то есть данный четырёхугольник не является квадратом,
но около него можно описать окружность
А ложно
и
В ложно
то есть данный четырёхугольник не является квадратом,
и около него нельзя описать окружность
(разумеется, это справедливо не для всякого четырёхугольника)
Ложен только один вариант:
25
А истинно
и
В ложно
то есть данный четырёхугольник является квадратом,
но около него нельзя описать окружность
26.
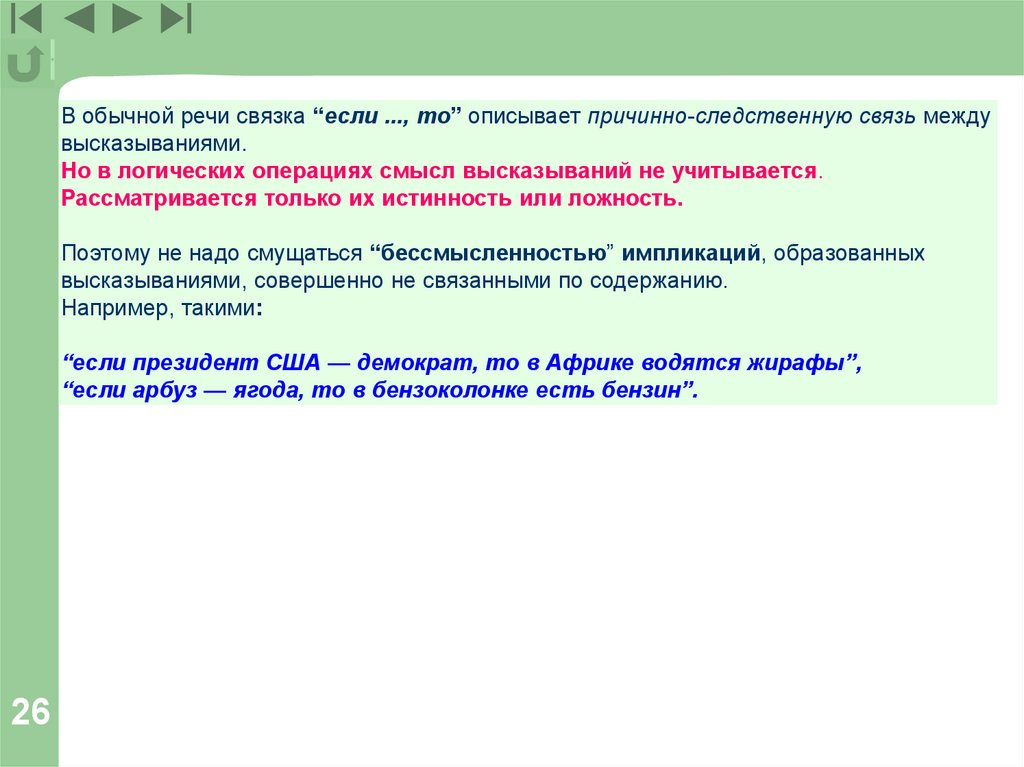
В обычной речи связка “если ..., то” описывает причинно-следственную связь междувысказываниями.
Но в логических операциях смысл высказываний не учитывается.
Рассматривается только их истинность или ложность.
Поэтому не надо смущаться “бессмысленностью” импликаций, образованных
высказываниями, совершенно не связанными по содержанию.
Например, такими:
“если президент США — демократ, то в Африке водятся жирафы”,
“если арбуз — ягода, то в бензоколонке есть бензин”.
26
27.
ЭКВИВАЛЕНЦИЯ (ДВОЙНАЯ ИМПЛИКАЦИЯ)Операция, выражаемая связками “тогда и только тогда”, "необходимо и
достаточно”, “... равносильно ...”, называется эквиваленцией или двойной
импликацией и обозначается знаком ↔ или ~ .
Высказывание А ↔ В истинно тогда и только тогда, когда значения А и В
совпадают.
Например,
высказывания
“24 делится на 6 тогда и только тогда, когда 24 делится на 3”,
“23 делится на 6 тогда и только тогда, когда 23 делится на 3”
истинны,
а высказывания
“24 делится на 6 тогда и только тогда, когда 24 делится на 5”,
“21 делится на 6 тогда и только тогда, когда 21 делится на 3”
ложны.
Таблица истинности функции логического РАВЕНСТВА
27
x
0
0
1
1
y
0
1
0
1
x↔у
1
0
0
1
28.
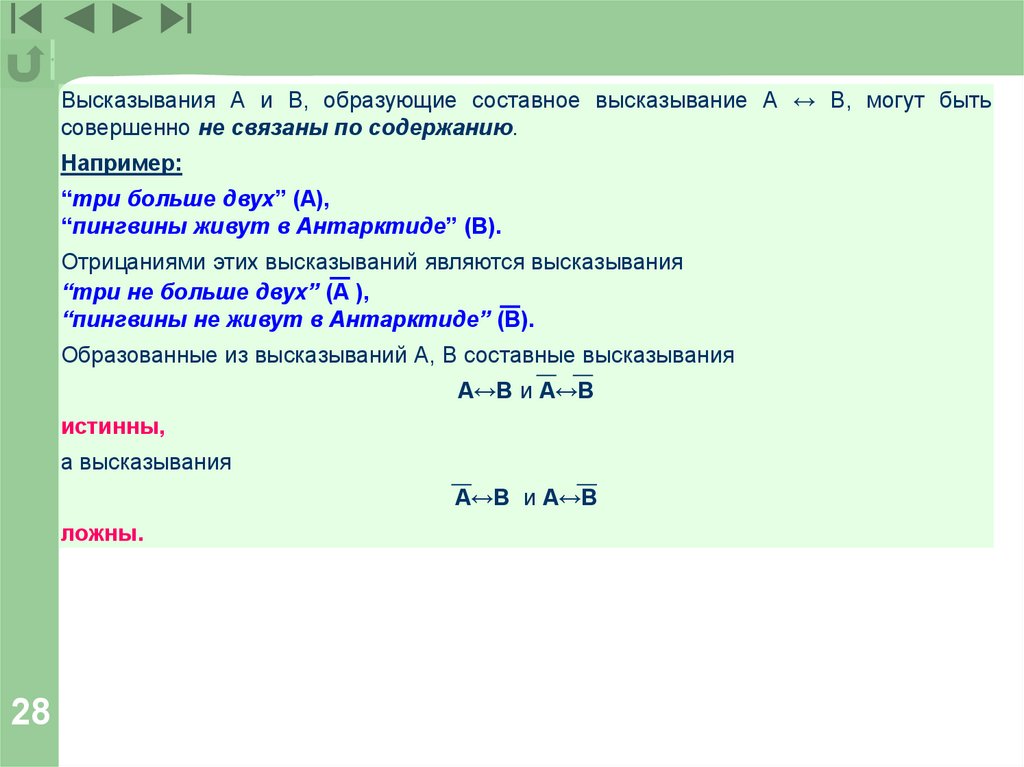
Высказывания А и В, образующие составное высказывание А ↔ В, могут бытьсовершенно не связаны по содержанию.
Например:
“три больше двух” (А),
“пингвины живут в Антарктиде” (В).
Отрицаниями этих высказываний являются высказывания
“три не больше двух” (А ),
“пингвины не живут в Антарктиде” (В).
Образованные из высказываний А, В составные высказывания
A↔B и А↔В
истинны,
а высказывания
A↔В и А↔B
ложны.
28
29.
Итак, нами рассмотрены пять логических операций:инверсия, конъюнкция, дизъюнкция, импликация и эквиваленция.
Импликацию можно выразить через дизъюнкцию и инверсию:
А→ В = А v В.
Эквиваленцию можно выразить через отрицание, дизъюнкцию и конъюнкцию:
А ↔ В = (А v В) • (А v В).
Таким образом, операций отрицания, дизъюнкции и конъюнкции достаточно,
чтобы описывать и обрабатывать логические высказывания.
Порядок выполнения логических операций задается круглыми скобками.
Но для уменьшения числа скобок договорились считать, что
1. инверсия (“не”),
2. конъюнкция (“и”),
3. дизъюнкция (“или”)
4. импликация.
29
30.
30З а д а ч и.
№7. Определите значения истинности высказываний:
а) “наличия аттестата о среднем образовании достаточно для поступления
в институт”;
б) “наличие аттестата о среднем образовании необходимо для поступления
в институт”;
в) “если целое число делится на 6, то оно делится на 3”;
г) “подобие треугольников является необходимым условием их равенства”;
д) “подобие треугольников является необходимым и достаточным условием
их равенства”;
е) “треугольники подобны только в случае их равенства”;
ж) “треугольники равны только в случае их подобия”;
з) “равенство треугольников является достаточным условием их подобия”;
и) “для того, чтобы треугольники были неравны, достаточно, чтобы они
были неподобны”;
к) “для того, чтобы четырёхугольник был квадратом, достаточно, чтобы
его диагонали были равны и перпендикулярны”.
ОТВЕТ:
Истинны: б), в), г), з), к), и);
Ложны: а), д), е), ж).
























 informatics
informatics








