Ремизов

1.

Государственное профессиональное образовательное автономное
учреждение Ярославской области Ростовский колледж отраслевых
технологий
«Российские ученые, внесшие значительный вклад в
развитие науки XXI века»
Иван Ремизов: новый этап в теории
дифференциальных уравнений
Участник:
Руководитель: Богословская В.Е.

2.

Цели и задачи доклада
Цель: проанализировать суть концептуального прорыва И. Ремизова в
теории дифференциальных уравнений и оценить его влияние на развитие
математической науки.
Задачи:
1.
Изучить исторический контекст развития теории дифференциальных
уравнений до работ И. Ремизова.
2.
Проанализировать суть концептуального прорыва, предложенного И.
Ремизовым.
3.
Выявить ключевые отличия нового подхода от традиционных методов
решения.
4.
Оценить практическое значение открытий И. Ремизова для
современной математики и обозначить перспективы дальнейшего
развития теории на основе идей исследователя.

3.

Дифференциальное уравнение
Дифференциальным уравнением называется соотношение, связывающее независимую переменную
х, искомую функцию y=f(x) и её производные.
Решением дифференциального уравнения называется любая функция y=f(x), которая при подстановке в это
уравнение обращает его в тождество.
Порядок старшей производной, входящей в дифференциальное уравнение, называется порядком данного
уравнения.
(Пример: y’ – y = 0 – дифференциальное уравнение 1-го порядка; y’’ + y = 0 – дифференциальное уравнение 2-го
порядка).
Решение дифференциального уравнения не является единственным. Общее решение дифференциального
уравнения – это множество решений, содержащее все без исключения решения этого дифференциального
уравнения. Для определения единственного решения дифференциального уравнения задаются
дополнительные условия.

4.

Основные этапы развития
дифференциальных уравнений
Зарождение (XVII век). Появление
инструментов дифференциального
исчисления, Ньютон и Лейбниц впервые
формулируют основные задачи механики и
анализа в терминах производных и уравнений.
Исаак Ньютон
Готфрид Вильгельм
Лейбниц

5.

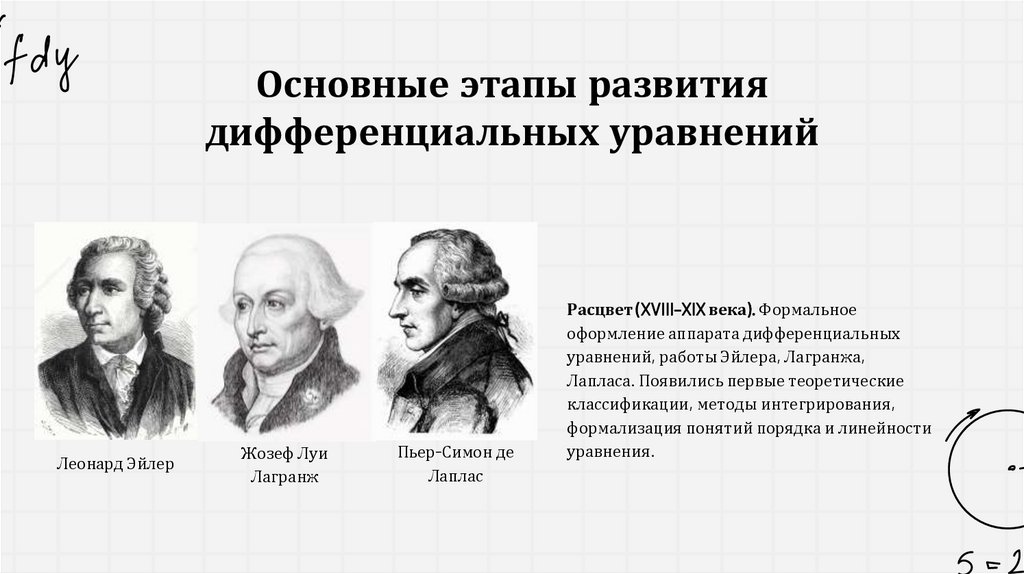
Основные этапы развития
дифференциальных уравнений
Леонард Эйлер
Жозеф Луи
Лагранж
Пьер-Симон де
Лаплас
Расцвет (XVIII–XIX века). Формальное
оформление аппарата дифференциальных
уравнений, работы Эйлера, Лагранжа,
Лапласа. Появились первые теоретические
классификации, методы интегрирования,
формализация понятий порядка и линейности
уравнения.

6.

Основные этапы развития
дифференциальных уравнений
XIX век. Дифференциальные уравнения
заняли центральное место в математическом
описании теплопроводности, электричества,
волн и других явлений, чему способствовали
работы Фурье, Пуассона и Коши.
Шарль Фурье
Симеон Дени
Пуассон
Огюстен Луи
Коши

7.

Основные этапы развития
дифференциальных уравнений
Новый этап развития — работы Анри
Пуанкаре (1854–1912). Созданная им
«качественная теория дифференциальных
уравнений» вместе с теорией функций
комплексных переменных легла в основу
современной топологии.
Анри Пуанкаре

8.

Ремизов Иван Дмитриевич
Начал работать в НИУ ВШЭ в 2018 году.
Научно-педагогический стаж: 6 лет.
Полномочия / обязанности:
проведение исследований, написание статей и научных отчетов;
участие в конференциях, мастер-классах, воркшопах, летних
школах;
участие в подготовке и организации мероприятий лаборатории;
координация деятельности молодых членов научного коллектива.
Oбразование и учёные степени:
2018 Кандидат физико-математических наук: Московский
государственный университет им. М.В. Ломоносова
2008 Специалитет: Московский государственный университет им.
М.В. Ломоносова, специальность «Математика», квалификация
«математик»

9.

Суть концептуального прорыва Ремизова
Ремизов расширил набор допустимых
математических операций, добавив нахождение
предела последовательности. что позволило
записать формулу, в которую можно подставить
коэффициенты a, b, c и g уравнения ay''+ by'+cy=g, и
найти его решение — функцию y.
Разработал, совместно с коллегой Олегом
Иван Ремизов
Олег Галкин
Галкиным, метод, основанный на теории
аппроксимаций Чернова, где сложный процесс
«разрезается» на бесконечное число мелких
простых шагов и с помощью преобразования
Лапласа эти аппроксимации собираются в точное
решение (резольвенту).
Статья Ивана Ремизова
https://www.vmj.ru/articles/2025_4_10.pdf#/

10.

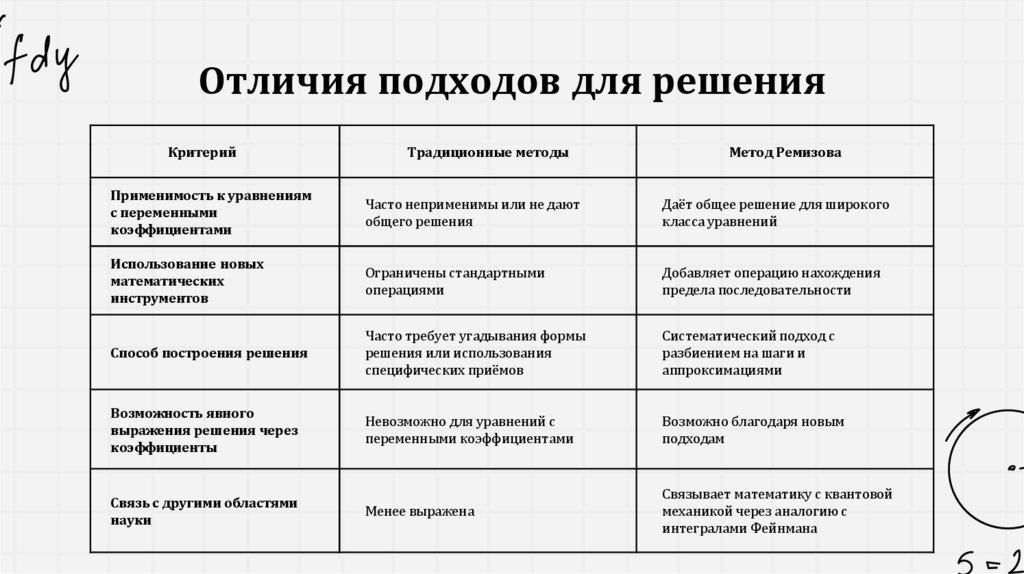
Отличия подходов для решения
Критерий
Традиционные методы
Метод Ремизова
Применимость к уравнениям
с переменными
коэффициентами
Часто неприменимы или не дают
общего решения
Даёт общее решение для широкого
класса уравнений
Использование новых
математических
инструментов
Ограничены стандартными
операциями
Добавляет операцию нахождения
предела последовательности
Способ построения решения
Часто требует угадывания формы
решения или использования
специфических приёмов
Систематический подход с
разбиением на шаги и
аппроксимациями
Возможность явного
выражения решения через
коэффициенты
Невозможно для уравнений с
переменными коэффициентами
Возможно благодаря новым
подходам
Связь с другими областями
науки
Менее выражена
Связывает математику с квантовой
механикой через аналогию с
интегралами Фейнмана

11.

Практическое значение прорыва Ремизова
Физика высоких энергий
В Большом адронном коллайдере протоны
разгоняют почти до скорости света. До
открытия Ремизова физики полагались на
численные симуляции. Теперь можно
получать точные аналитические решения,
что упростит калибровку ускорителей и
ускорит обработку данных экспериментов.

12.

Практическое значение прорыва Ремизова
Космические технологии
Траектории спутников описываются
дифференциальными уравнениями второго
порядка. Формула Ремизова даёт точное
аналитическое решение, что повысит
точность навигации и сократит время
расчёта орбит для новых спутников. При
планировании миссий к другим планетам
или корректировке траектории зондов
инженеры смогут ускорять вычисления в
десятки раз.

13.

Практическое значение прорыва Ремизова
Экономика
Дифференциальные уравнения второго
порядка используются в макроэкономических
моделях, учитывающих не только текущее
состояние рынка, но и скорость изменений, и
ускорение процессов. Формула Ремизова
позволит экономистам быстрее строить
прогнозы, Центробанкам — точнее оценивать
инфляционные риски, компаниям —
предсказывать колебания спроса.

14.

Практическое значение прорыва Ремизова
Инженерия
Колебания конструкций под нагрузкой
(мосты, небоскрёбы, турбины) описываются
этими уравнениями. Аналитическое
решение упростит проектирование и
анализ устойчивости конструкций, снизит
затраты на численные расчёты.

15.

Заключение
Открытие Ремизова — это не просто решение частной математической задачи, а
смена взглядов в подходе к дифференциальным уравнениям.
Оно доказывает, что даже «закрытые» проблемы могут быть решены через
расширение математического инструментария, создаёт фундамент для новых
открытий в физике, инженерии и других науках и демонстрирует силу
междисциплинарных исследований, объединяющих классическую математику и
современные физические теории.

16.

Источники
1.
2.
3.
4.
5.
6.
7.
https://www.vmj.ru/articles/2025_4_10.pdf#/
https://www.hse.ru/news/science/1122687898.html
https://www.hse.ru/news/development/1063531804.html
https://www.hse.ru/org/persons/215573332/
https://yandex.ru/images/search
https://bigenc.ru/c/differentsial-noe-uravnenie-7e57fc
https://resh.edu.ru/subject/lesson/4926/main/225845/