19_Второй признак подобия_25

1.

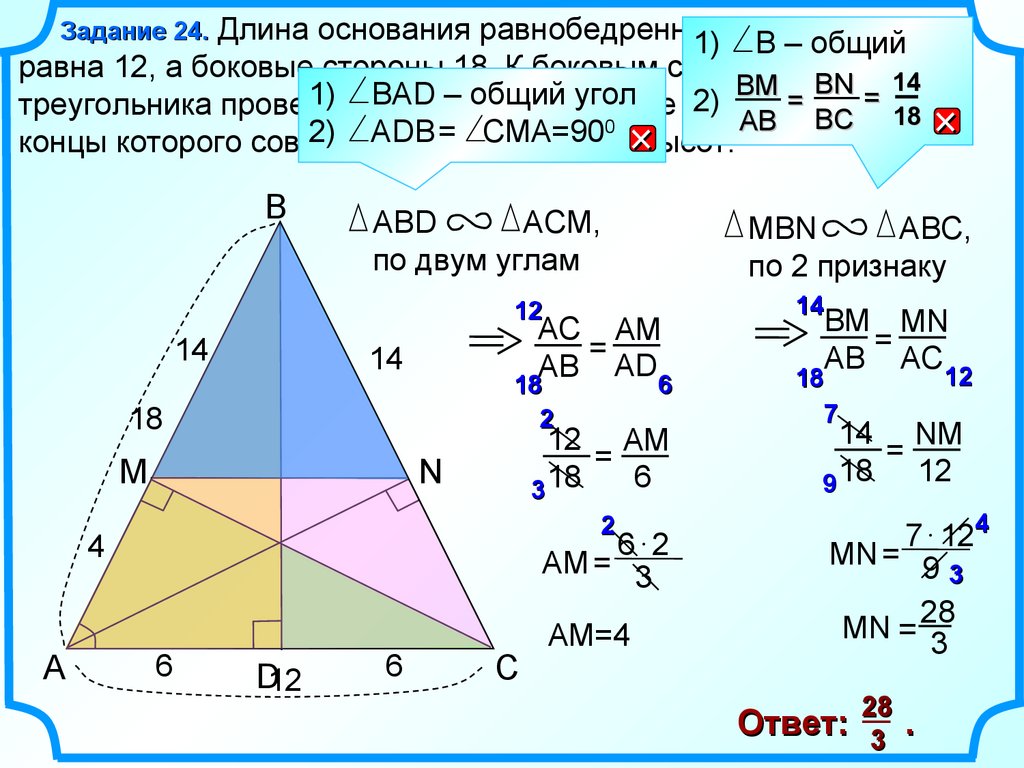
Задание 24. Длина основания равнобедренного треугольника
1) В – общий
равна 12, а боковые стороны 18. К боковым сторонам
BM BN = 14
1)
BAD
–
общий
угол
=
2)
треугольника проведены высоты. Вычислите длину
отрезка,
18
BC
AB
0
2) ADB
CMA=90 высот.
концы которого совпадают
с=
основаниями
В
ABD
АCM,
по двум углам
MBN
АBC,
по 2 признаку
12
14
AС АМ
=
АB AD
14
18
2
18
М
12 АМ
=
6
18
3
N
2
4
А
6
6 2
АМ = 3
6
D12
6
С
АМ=4
14
BM МN
=
АB AC
18
7
12
14 NМ
=
12
9 18
7 124
МN = 9
3
28
МN =
3
28
Ответ: 3 .

2.

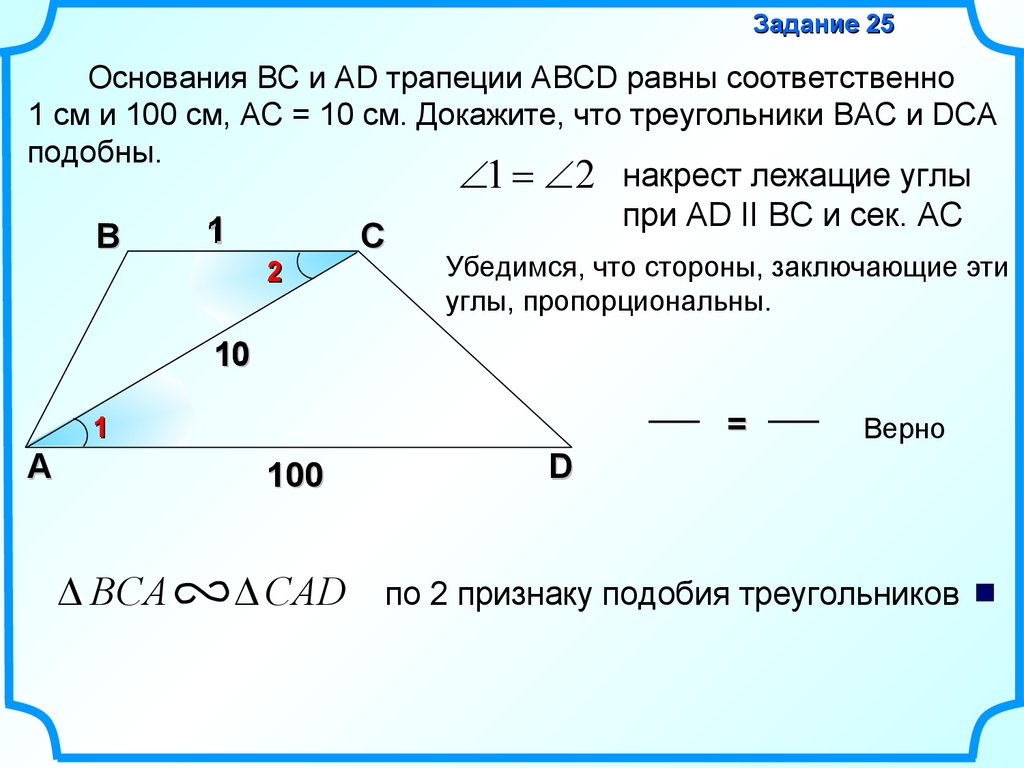
Задание 25
Основания BC и AD трапеции ABCD равны соответственно
1 см и 100 см, AC = 10 см. Докажите, что треугольники BAС и DCA
подобны.
1 2 накрест лежащие углы
при AD II BC и сек. AС
1
B
C
2
Убедимся, что стороны, заключающие эти
углы, пропорциональны.
10
=
1
A
100
BCA
CAD
Верно
D
по 2 признаку подобия треугольников

3.

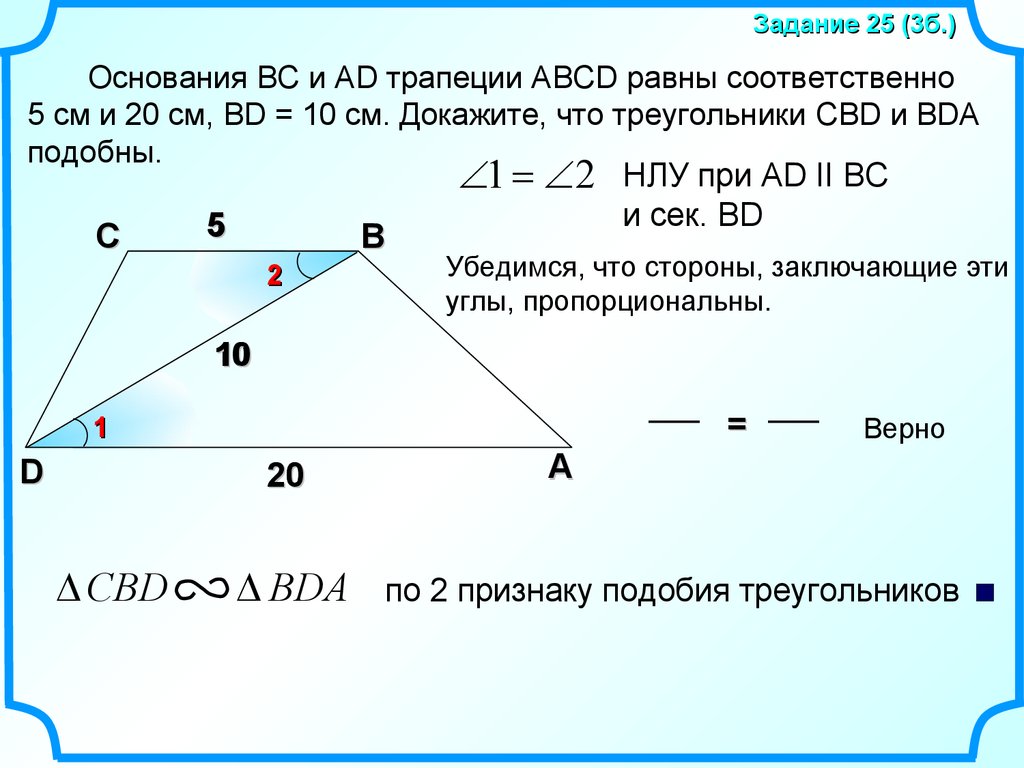
Задание 25 (3б.)
Основания BC и AD трапеции ABCD равны соответственно
5 см и 20 см, BD = 10 см. Докажите, что треугольники CBD и BDA
подобны.
1 2 НЛУ при AD II BC
и сек. BD
5
C
B
2
Убедимся, что стороны, заключающие эти
углы, пропорциональны.
10
=
1
D
20
CBD
BDA
Верно
A
по 2 признаку подобия треугольников

4.

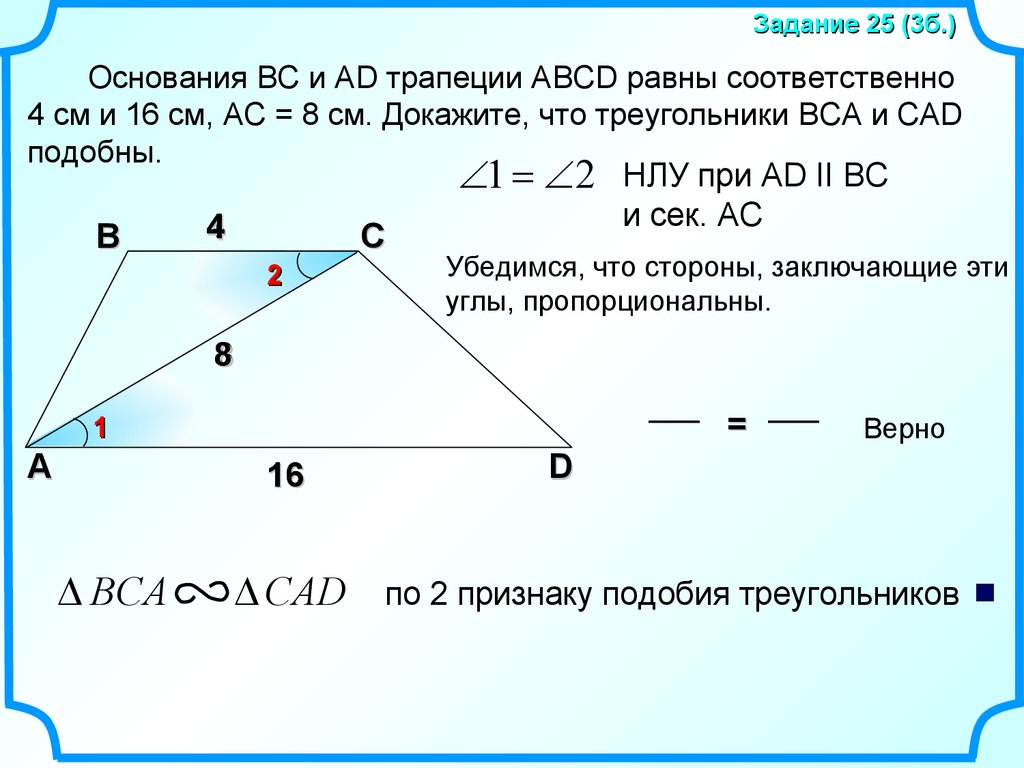
Задание 25 (3б.)
Основания BC и AD трапеции ABCD равны соответственно
4 см и 16 см, AC = 8 см. Докажите, что треугольники BCA и CAD
подобны.
1 2 НЛУ при AD II BC
и сек. AС
4
B
C
2
Убедимся, что стороны, заключающие эти
углы, пропорциональны.
8
=
1
A
16
BCA
CAD
Верно
D
по 2 признаку подобия треугольников

5.

6.

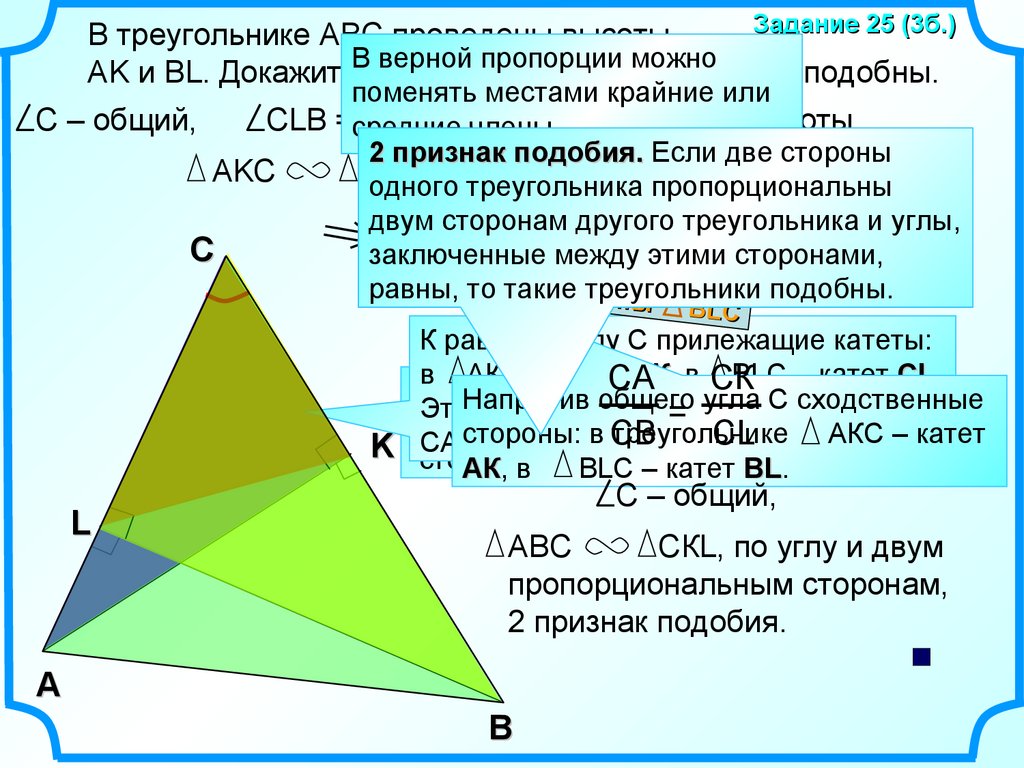
Задание 25 (3б.)
В треугольнике АВС проведены высоты
В верной пропорции можно
AK и BL. Докажите,
что треугольники ABC и CKL подобны.
поменять местами крайние или
C – общий,
CLB =средние
AKC =члены.
900, т.к. BL и AK – высоты
2 признак подобия. Если две стороны
АKС
BLC,
по двум углам, 1 признак подобия.
одного треугольника пропорциональны
АКС
ы
н
о
р
двумCA
сторонам
другого
треугольника
и углы,
о
т
С
СК
АК
C
заключенные
= этими сторонами,
= между
равны,
треугольники
подобны.
Стор
CBто такие
СL
BL
оны
BLС
К равному углу С прилежащие катеты:
в АКС – катет
СК,
BLC – катет СL.
СК в СК
CA
Запишем
отношение
сходственных
общего
угла равных
С сходственные
ЭтиНапротив
катеты лежат
против
углов
=
сторон.
Напротив
равных
прямых
углов
треугольнике
АКС – катет
СL
САКстороны:
и СВL. в CB
K стороны
и СВ–(катет
гипотенузы)
гипотенузы
АК,
BL.
АК в СА BLC
BL
L
C – общий,
АВС
СКL, по углу и двум
пропорциональным сторонам,
2 признак подобия.
A
B

7.

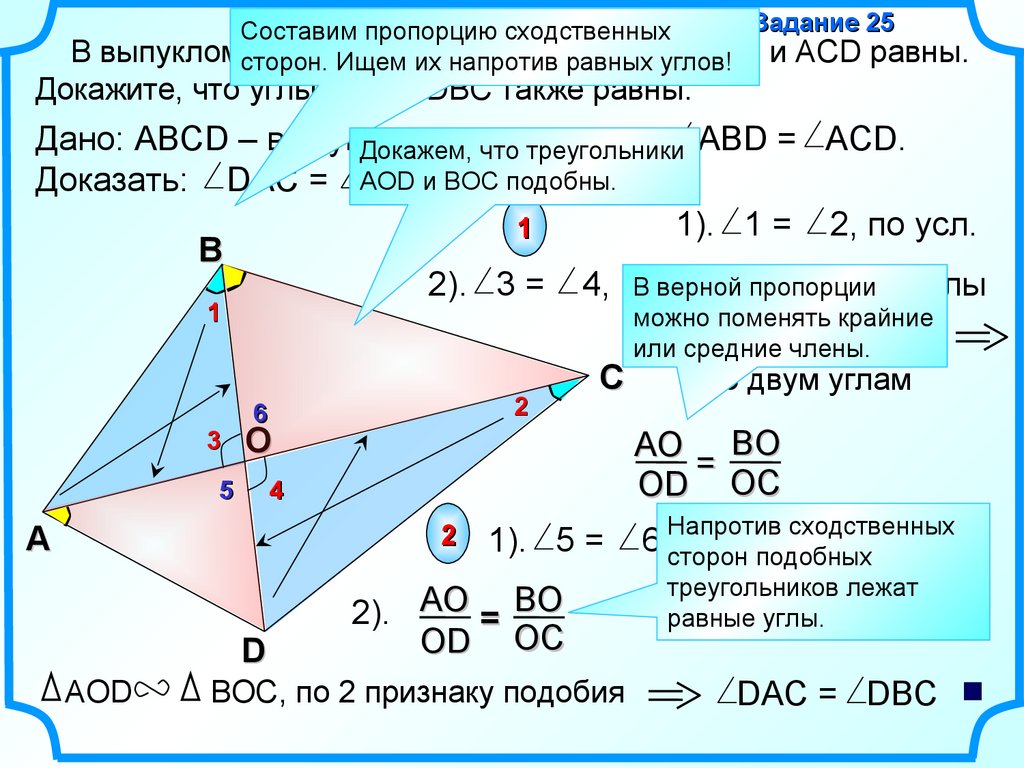
Задание 25
Составим пропорцию сходственных
В выпукломсторон.
четырехугольнике
АВСD
углы
АВD и АСD равны.
Ищем их напротив
равных
углов!
Докажите, что углы DАС и DВС также равны.
Дано: ABCD – выпук.Докажем,
четырехугольник,
что треугольники ABD = ACD.
и BOC подобны.
Доказать: DАС = AOD
DBC.
1). 1 = 2, по усл.
1
B
2). 3 = 4, как
вертикальные
В верной
пропорции углы
1
2
6
3
O
5
4
D
AOD
по двум углам
AO BO
=
OD OC
2
A
C
можно поменять крайние
ABO члены.
DCO,
или средние
1). 5 =
2). AO = BO
OD OC
BOC, по 2 признаку подобия
Напротив сходственных
6,сторон
вертикальные
углы
подобных
треугольников лежат
равные углы.
DAC = DBC

8.

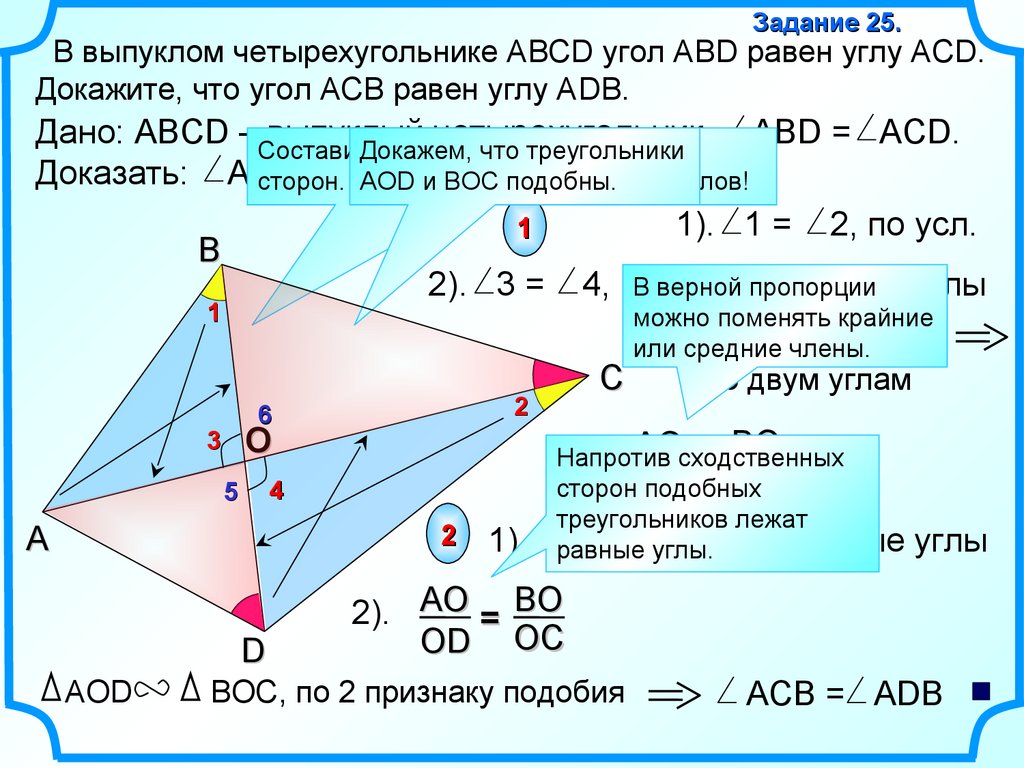
Задание 25.
В выпуклом четырехугольнике АВСD угол АВD равен углу АСD.
Докажите, что угол АСВ равен углу АDВ.
Дано: ABCD –Составим
выпуклый
четырехугольник,
ABD = ACD.
Докажем,
пропорцию
что сходственных
треугольники
Доказать: АСВ
= Ищем
АDB.
сторон.
AOD
иих
BOC
напротив
подобны.
равных углов!
1). 1 = 2, по усл.
1
B
2). 3 = 4, как
вертикальные
В верной
пропорции углы
1
2
6
O
3
4
5
2
A
D
AOD
C
1).
можно поменять крайние
ABO члены.
DCO,
или средние
по двум углам
BO
AOсходственных
Напротив
=
OC
сторонOD
подобных
треугольников лежат
5
= 6,
вертикальные углы
равные
углы.
2). AO = BO
OD OC
BOC, по 2 признаку подобия
ACВ = АDB

9.

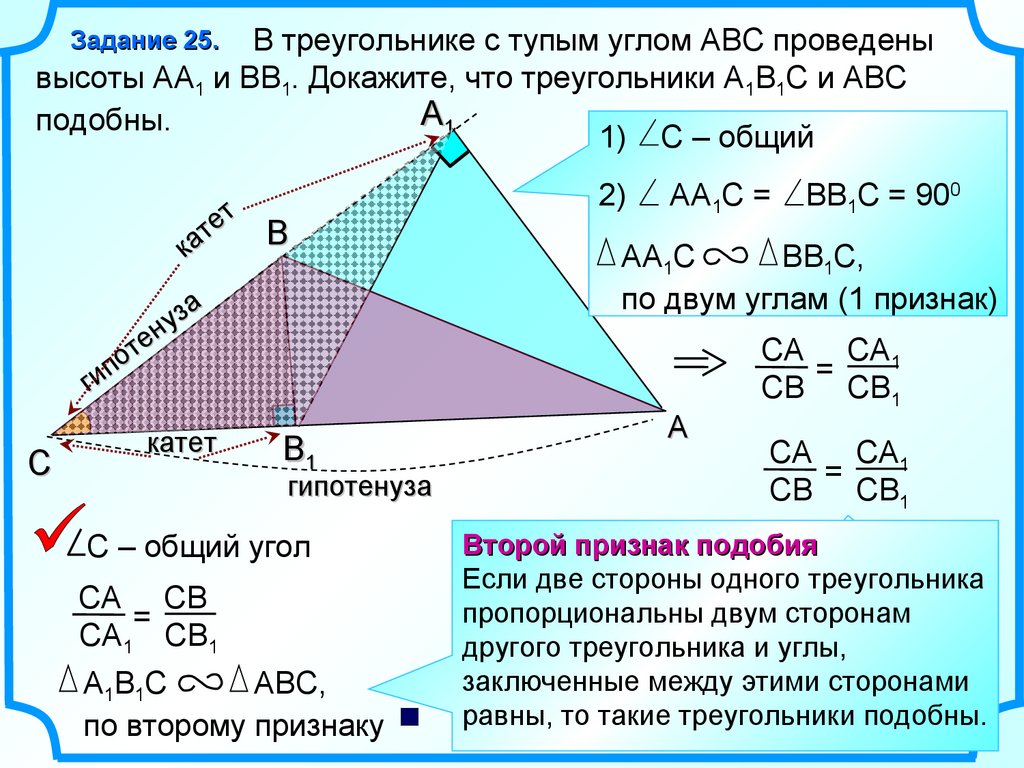
В треугольнике с тупым углом АВС проведены
высоты АА1 и ВВ1. Докажите, что треугольники А1В1С и АВС
А1
подобны.
1) С – общий
Задание 25.
т
е
т
B
ка
за
у
ен
т
по
и
г
С
катет
В1
гипотенуза
С – общий угол
СА СВ
=
СА1 CВ1
А1В1С
АВС,
по второму признаку
2)
АА1С =
ВВ1С = 900
АА1С
ВВ1С,
по двум углам (1 признак)
А
СА СA1
=
СВ CВ1
СА СA1
=
СВ CВ1
Второй признак подобия
Если двеСвойство
стороны одного
треугольника
пропорции.
пропорциональны
двум пропорции
сторонам
Если в верной
другого треугольника
и углы,средние
поменять местами
заключенные
между
этими сторонами
члены,
то получим
верную
равны, топропорцию.
такие треугольники подобны.

10.

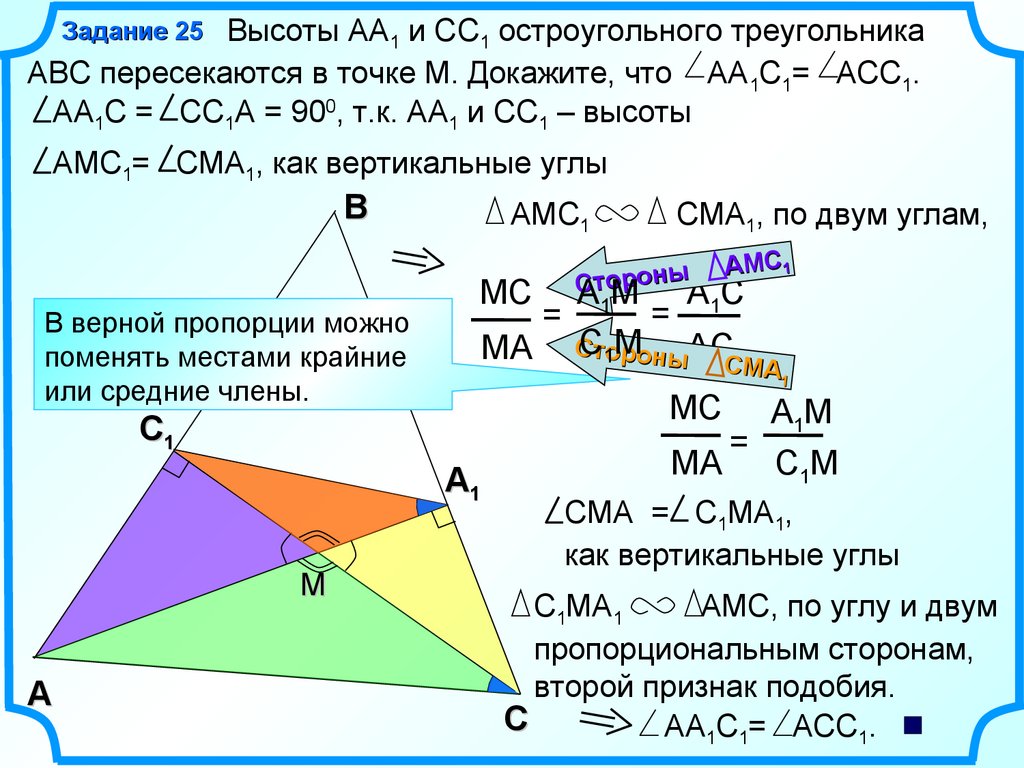
Высоты АА1 и СС1 остроугольного треугольника
ABC пересекаются в точке М. Докажите, что АА1С1= ACС1.
АА1С = CС1А = 900, т.к. АА1 и СС1 – высоты
Задание 25
АМС1= CМА1, как вертикальные углы
В
В верной пропорции можно
поменять местами крайние
или средние члены.
АМС1
МС
МА
А1
А
АМС 1
ы
н
о
р
о
С
Ат М А С
1
=
1
Ст1оМ
С
роныАСС1
МА
МС
С1
М
=
СМА1, по двум углам,
1
А1М
=
МА
С1М
СМА = C1МА1,
как вертикальные углы
С1МА1
АМС, по углу и двум
пропорциональным сторонам,
второй признак подобия.
C
АА1С1= ACС1.

11.

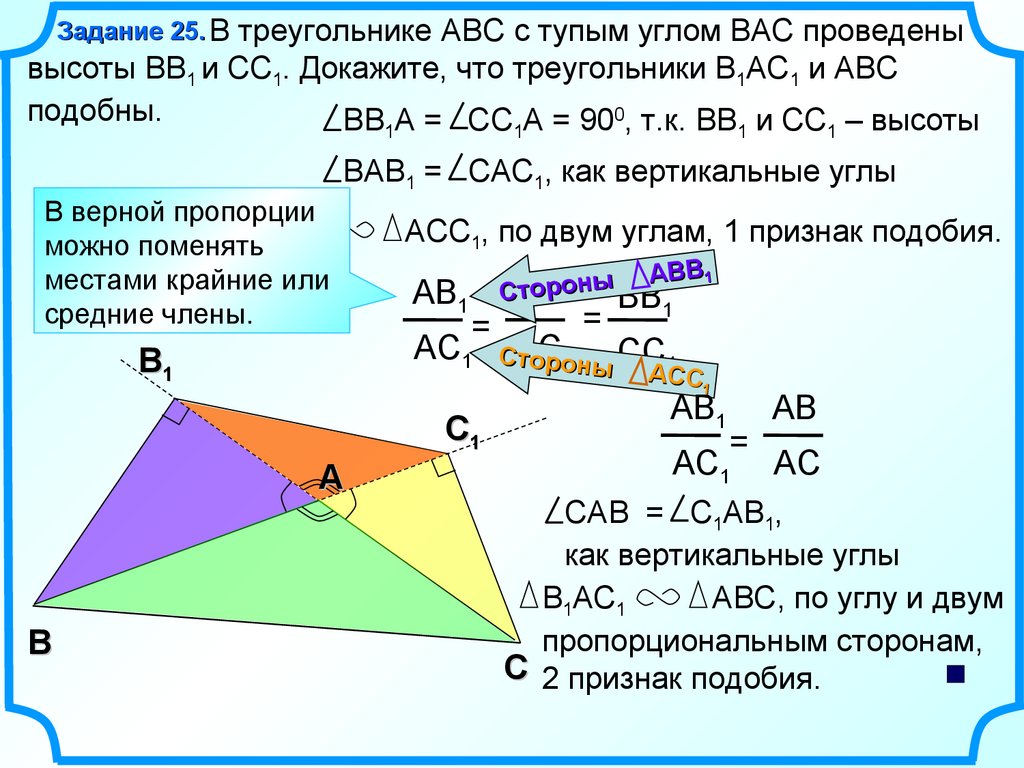
Задание 25. В треугольнике ABC с тупым углом ВАС проведены
высоты ВВ1 и СС1. Докажите, что треугольники В1АС1 и ABC
подобны.
BВ А = CС А = 900, т.к. BВ и СС – высоты
1
1
1
1
BАВ1 = CАС1, как вертикальные углы
В верной пропорции
АВВ1
можно поменять
местами крайние или
средние члены.
В1
АСС1, по двум углам, 1 признак подобия.
AВ1
=
АС1
=
1
САС
тороны СС1
АСС
1
С1
A
B
АВВ1
ы
н
о
р
то
САВ
ВВ
AВ1
=
АC1
АВ
АС
САВ = C1АВ1,
как вертикальные углы
В1АС1
АВС, по углу и двум
пропорциональным сторонам,
C 2 признак подобия.

12.

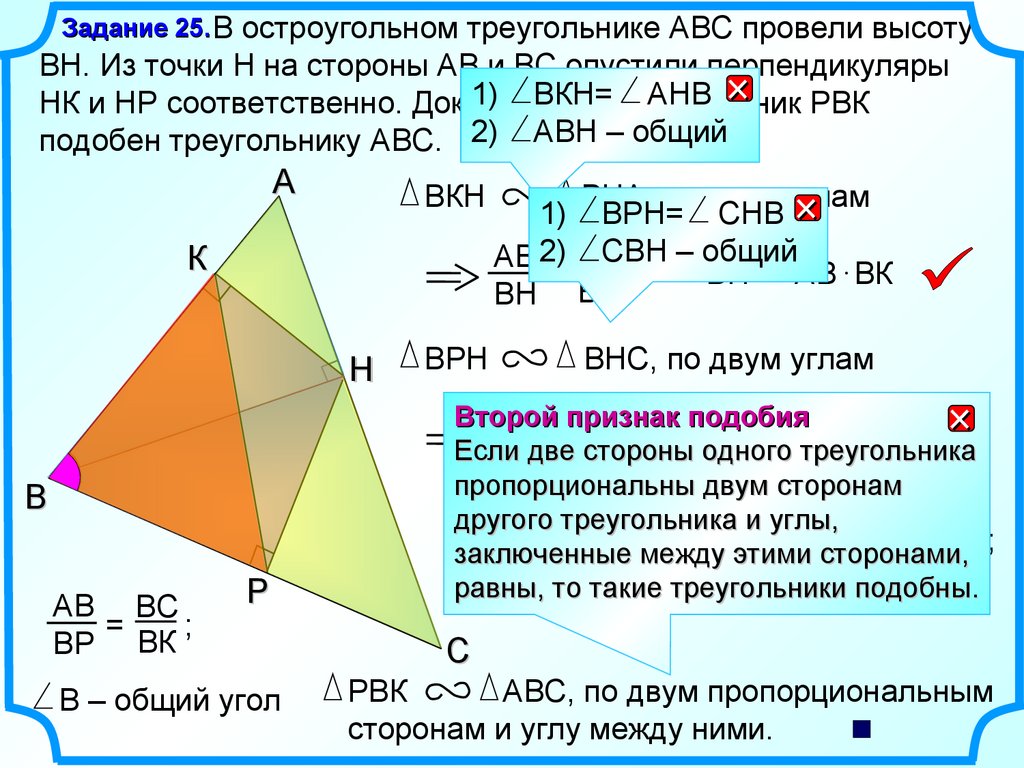
Задание 25. В остроугольном треугольнике АВС провели высоту
ВН. Из точки Н на стороны АВ и ВС опустили перпендикуляры
1) ВКН=
АНВ
НК и НР соответственно. Докажите,
что треугольник
РВК
подобен треугольнику АВС. 2) АВН – общий
А
ВКН
ВНА, по двум углам
1) ВРН= СНВ
СВН – общий
АВ 2) BН
ВН2 = АВ ВК
=
;
ВН ВК
ВРН
ВНС, по двум углам
К
Н
В
АВ BС
=
;
ВК
ВР
Р
B – общий угол
Второй
подобия
ВС признак
BН
2
ВР
ВН
=
ВС
=
;
Если
стороны одного треугольника
ВНдве ВР
пропорциональны двум сторонам
другого
треугольника и углы, АВ BС
АВ ВК = ВС ВР : (ВК ВР)
=
;
заключенные между этими сторонами,
ВК
ВР
ВР
ВР
ВК
ВК
равны, то такие треугольники подобны.
С
РВК
АВС, по двум пропорциональным
сторонам и углу между ними.

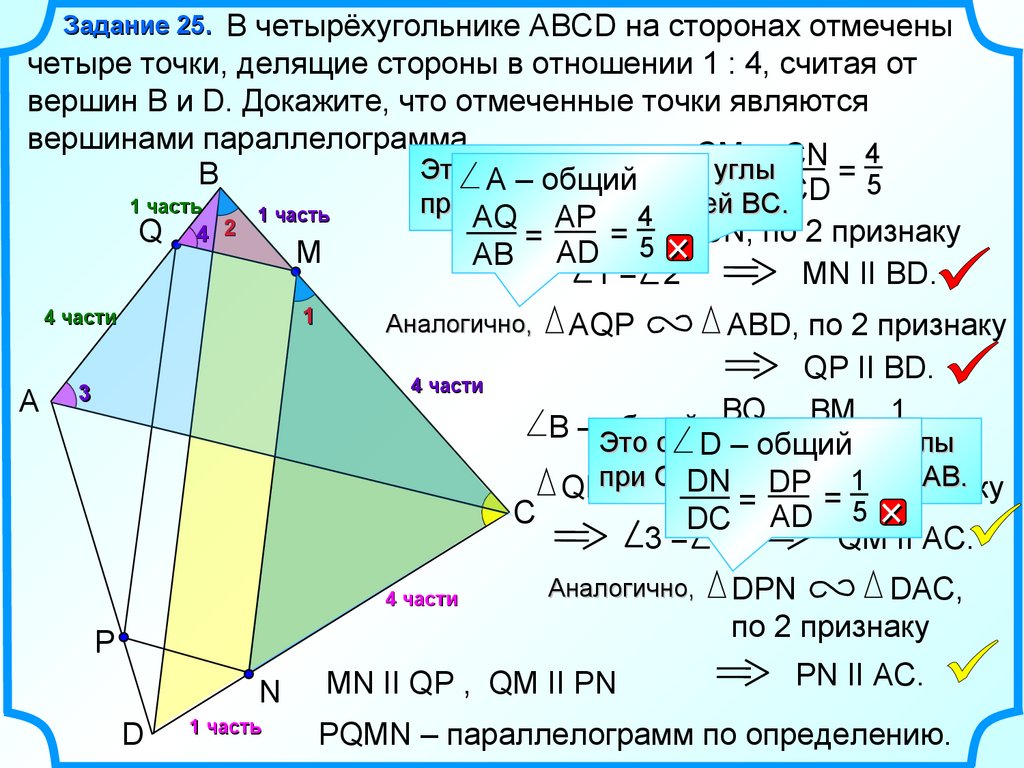
13.

Задание 25. В четырёхугольнике АВСD на сторонах отмечены
четыре точки, делящие стороны в отношении 1 : 4, считая от
вершин В и D. Докажите, что отмеченные точки являются
вершинами параллелограмма.
СМ
CN 4
Это
соответственные
углы
С
–
общий,
=5
=
B
А – общий
СBВС.CD
при MN и BD и секущей
1 часть
1 часть
AQBСD
AP 4 MCN, по 2 признаку
Q 4 2
=5
=
M
AB AD
1= 2
MN II BD.
1
4 части
А
4 части
3
ABD, по 2 признаку
QP II BD.
BQ BM 1
В – Это
общий,
= 5углы
=
соответственные
D BA
– общий
BC
при QMDN
иABC,
ACDP
и секущей
AВ.
1 признаку
QBM
по
2
=5
=
C
AD
DC
3= 4
QM II AC.
Аналогично,
4 части
AQP
Аналогично,
P
N
D
1 часть
MN II QP , QM II PN
DPN
DAC,
по 2 признаку
PN II AC.
PQMN – параллелограмм по определению.