Similar presentations:
9TViS-20_prezentatsia
1.
Что такое случайная величина?2.
ОпределениеСлучайная
величина
—
это
величина,
значение которой зависит от того, каким
элементарным
случайный опыт.
событием
закончился
3.
Чтотакое
вероятностей?
распределение
4.
Распределение вероятностейРаспределением
вероят ност ей
или
просто
распределением случайной величины называют закон,
который
каждому
значению
случайной
величины
ставит в соответствие вероятность того, что величина
примет это значение.
5.
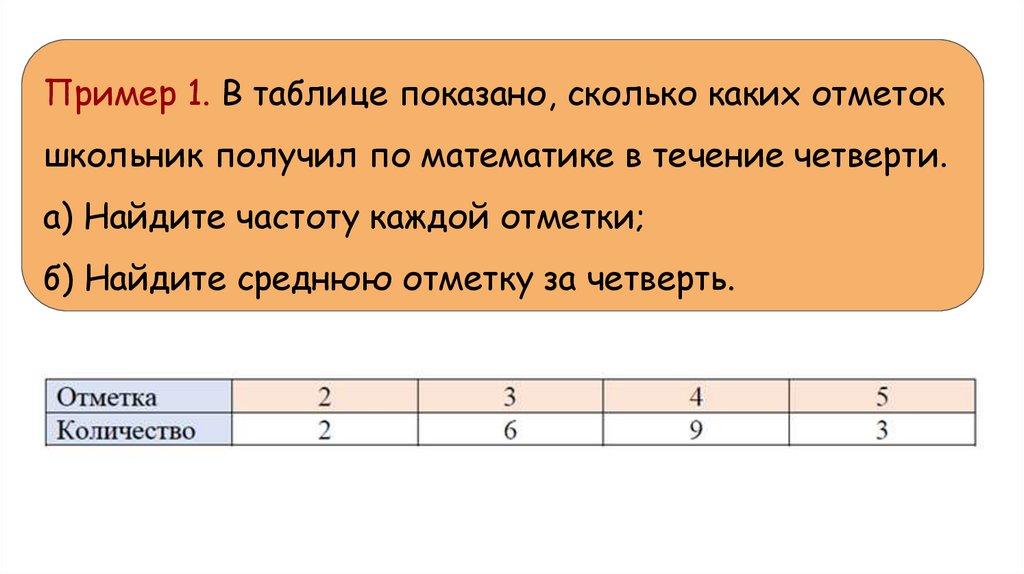
Пример 1. В таблице показано, сколько каких отметокшкольник получил по математике в течение четверти.
а) Найдите частоту каждой отметки;
б) Найдите среднюю отметку за четверть.
6.
Пример 1. В таблице показано, сколько каких отметокшкольник получил по математике в течение четверти.
а) Найдите частоту каждой отметки;
б) Найдите среднюю отметку за четверть.
Среднее арифметическое числового массива равно сумме
произведений различных значений на их частоты.
7.
Если умножить значенияслучайной величины на их
вероятности
и
сложить
произведения, то получится
некоторое среднее значение
случайной величины. Это
среднее
называют
математическим
ожиданием.
8.
9 классУрок №20
Примеры математического
ожидания как теоретического
среднего значения величины
9.
ОпределениеМатематическое
величины
—
ожидание
это
сумма
случайной
произведений
значений этой величины и их вероятностей.
Математическое
ожидание
случайной
величины X обозначают EX или E(X).
10.
Если случайная величина принимает всего nзначений х1, х2, х3,…, хn с вероятностями р1,
р2, р3,…, рn, то
11.
Вдальнейшем
для
распределений
упрощенно:
в
разделительных
примет вид:
простоты
таблицы
будем
изображать
скобках,
но
линий.
без
Распределение
12.
Математическоеожидание
называют
также
ожидаемым
значением
или
средним
значением
случайной
величины.
Математическое
ожидание
случайной величины измеряется в тех же единицах, что
и сама величина (средний рост — в сантиметрах, средняя
температура — в градусах).
13.
Пример 2. Пусть случайная величина X равначислу очков, выпавших на одной игральной кости.
Найти математическое ожидание этой величины.
14.
Пример 2. Пусть случайная величина X равначислу очков, выпавших на одной игральной кости.
Найти математическое ожидание этой величины.
В нашем примере математическое ожидание оказалось точно посередине
15.
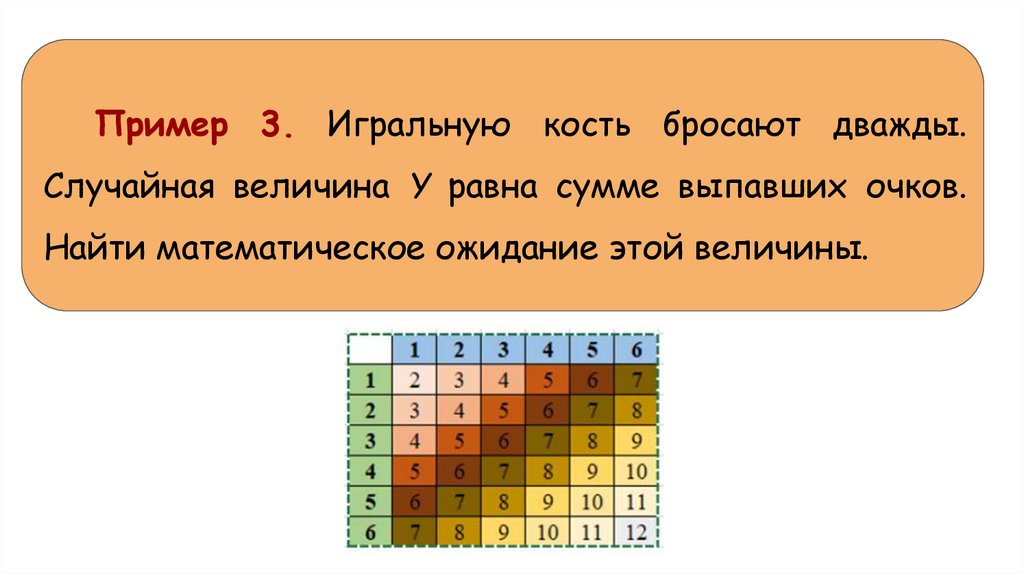
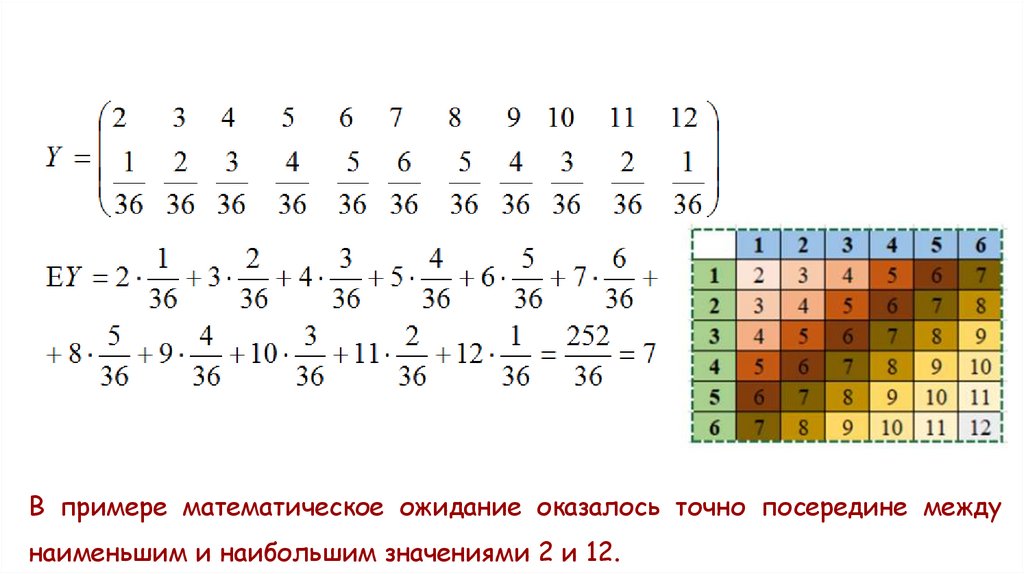
Пример 3. Игральную кость бросают дважды.Случайная величина Y равна сумме выпавших очков.
Найти математическое ожидание этой величины.
16.
В примере математическое ожидание оказалось точно посередине междунаименьшим и наибольшим значениями 2 и 12.
17.
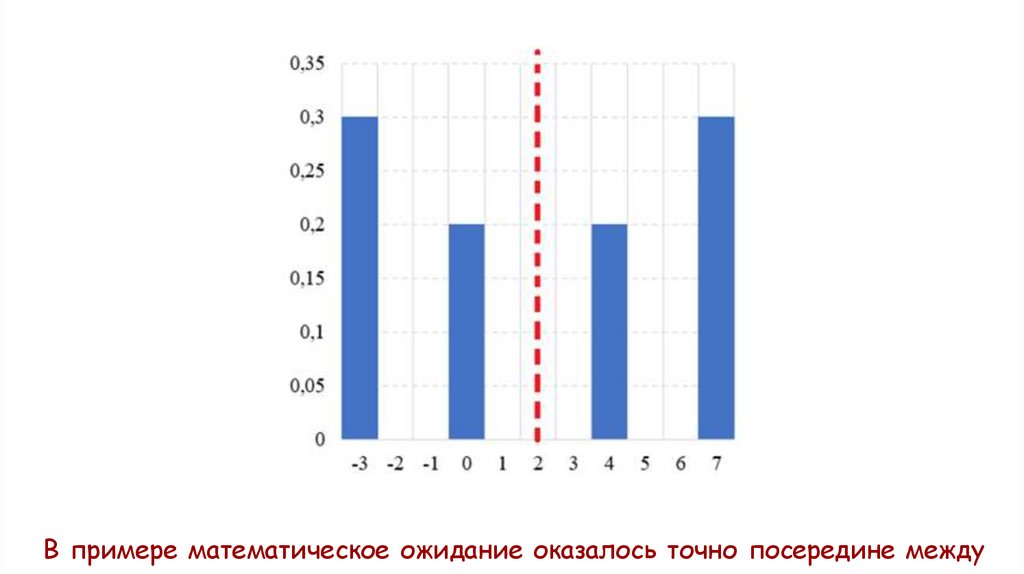
Пример4.
Задано
распределение
случайной
величины Х. Найти математическое ожидание и
построить
величины.
диаграмму
распределения
случайной
18.
Пример4.
Задано
распределение
случайной
величины Х. Найти математическое ожидание и
построить
величины.
диаграмму
распределения
случайной
19.
В примере математическое ожидание оказалось точно посередине между20.
Математическоеожидание
–
среднее
значение
случайной
величины
–
имеет
физический
центр
масс
диаграммы
смысл:
распределения.
















 mathematics
mathematics








