«Предел функции» 1курс

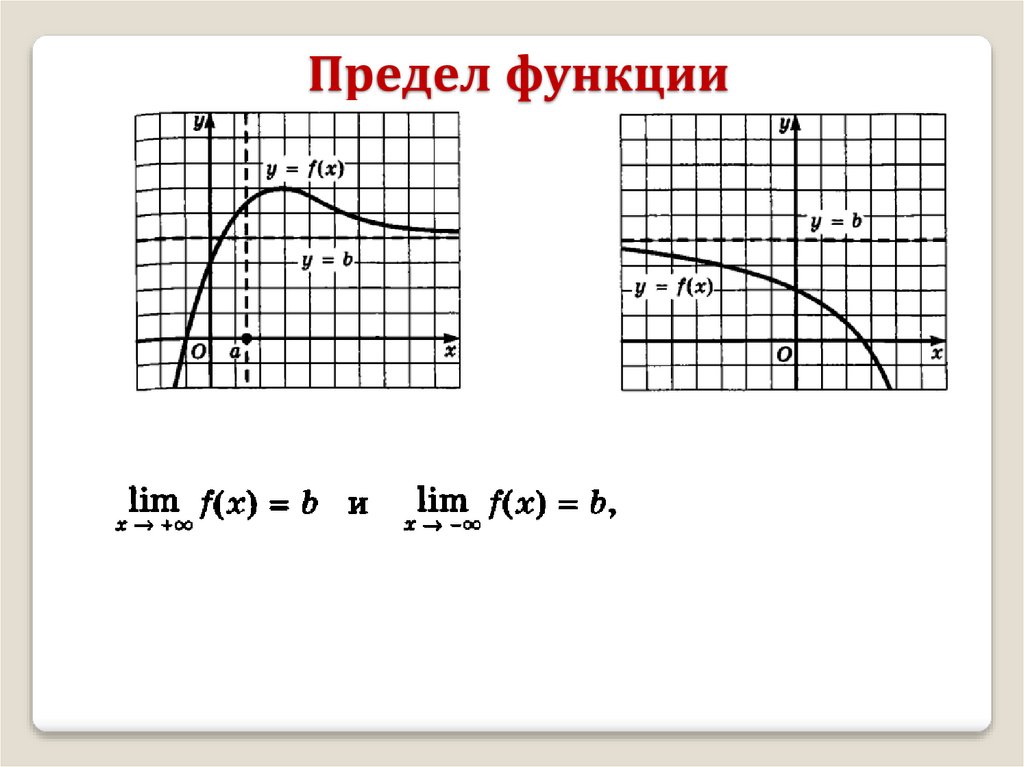
1. Предел функции

10 класс
Предел функции

2. Содержание

Определение предела последовательности
Предел функции
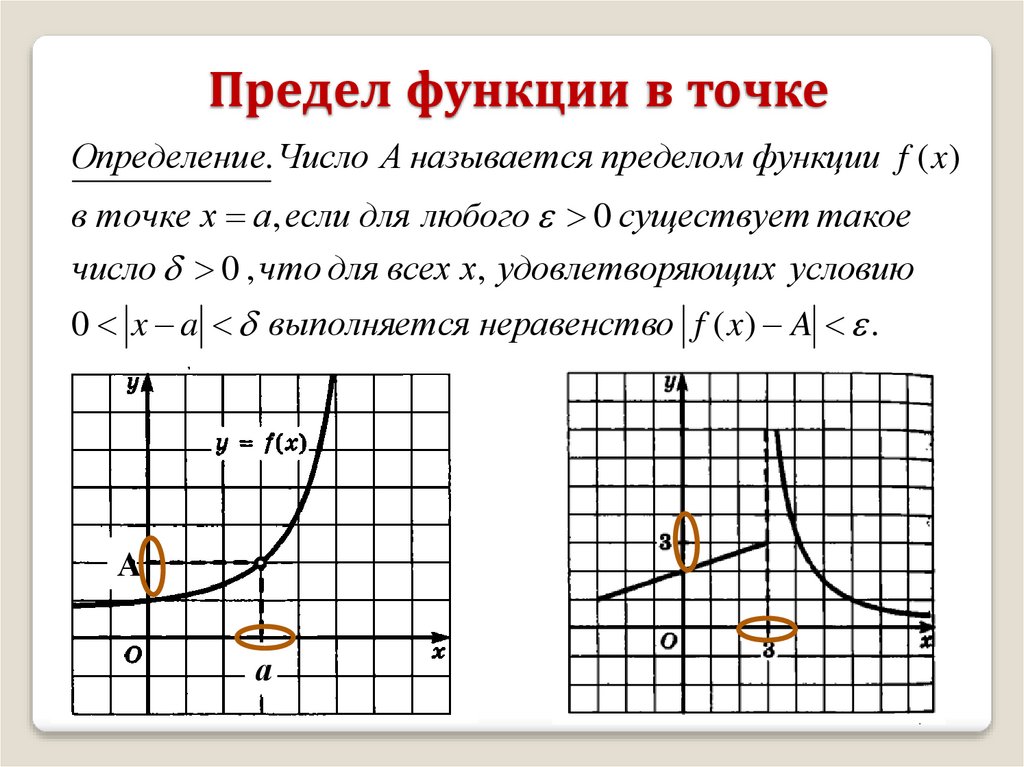
Предел функции в точке
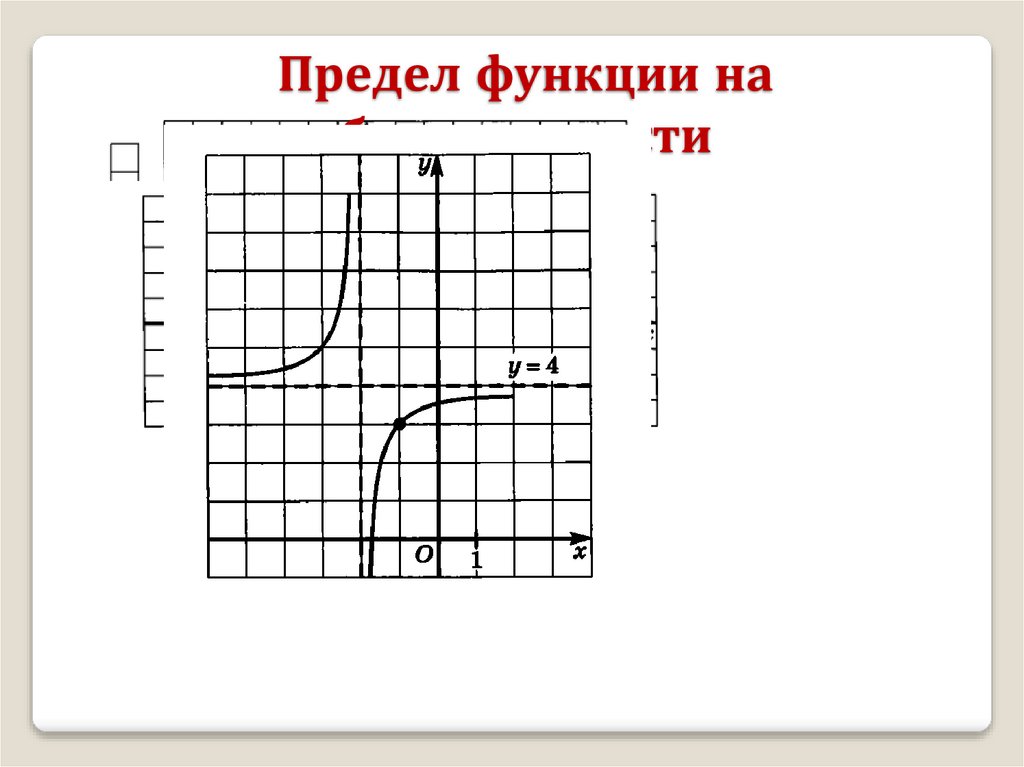
Предел функции на бесконечности
Приращение аргумента
Определение производной

3.

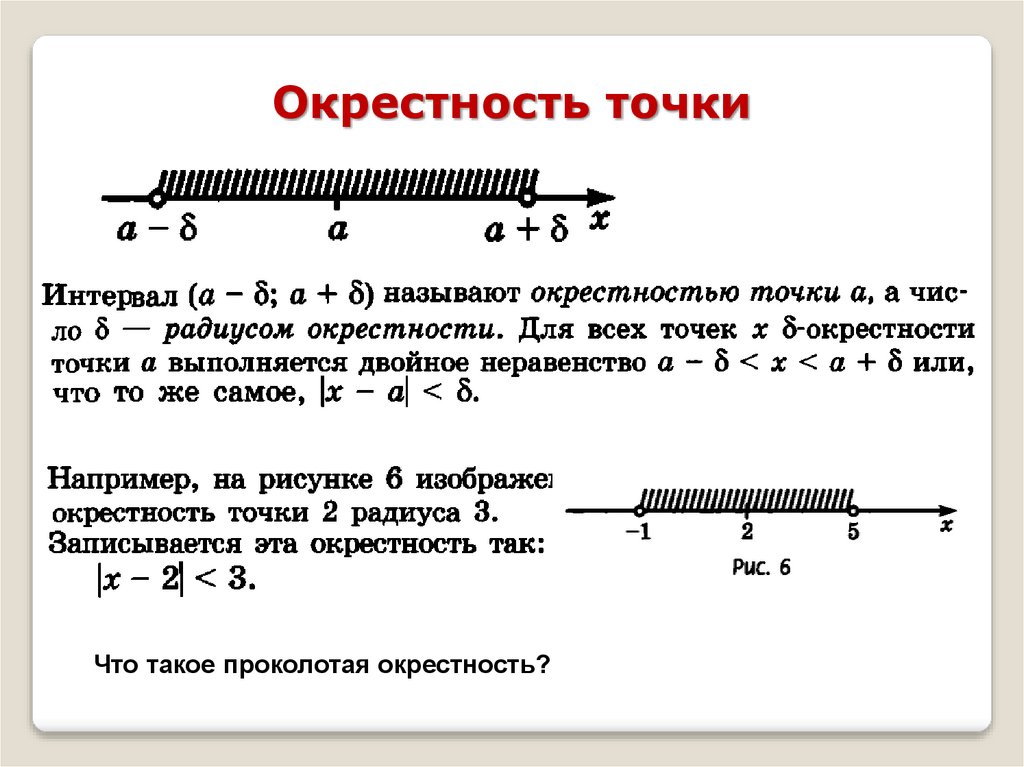
Окрестность точки
Что такое проколотая окрестность?

4.

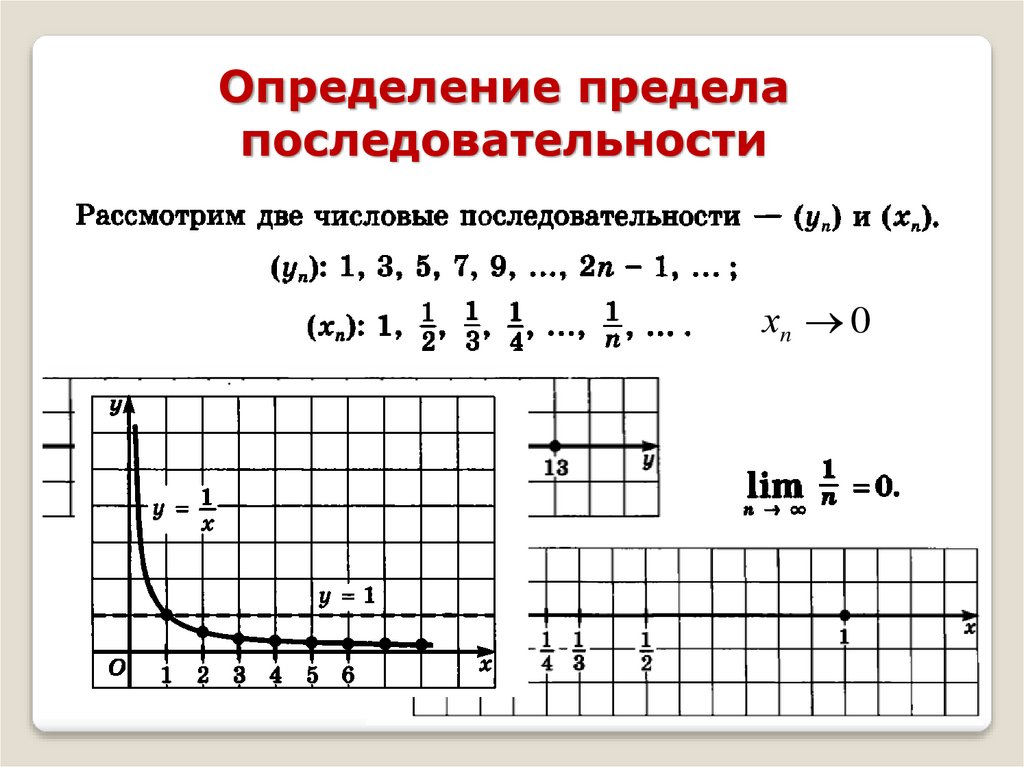
Определение предела
последовательности
хn 0

5.

6.

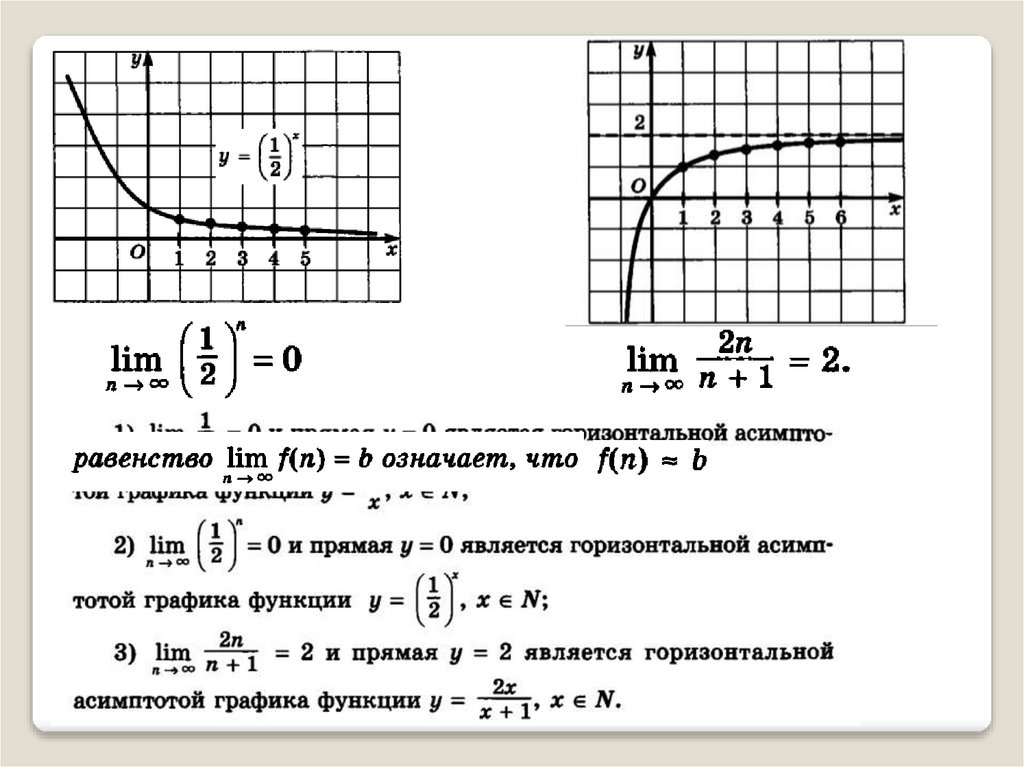
Примеры
1)
b1
Sn
1 q

7.

Примеры
lim 3 3
2)
n
3)
Решение:

8.

9.

10.

Примеры

11.

Предел функции

12.

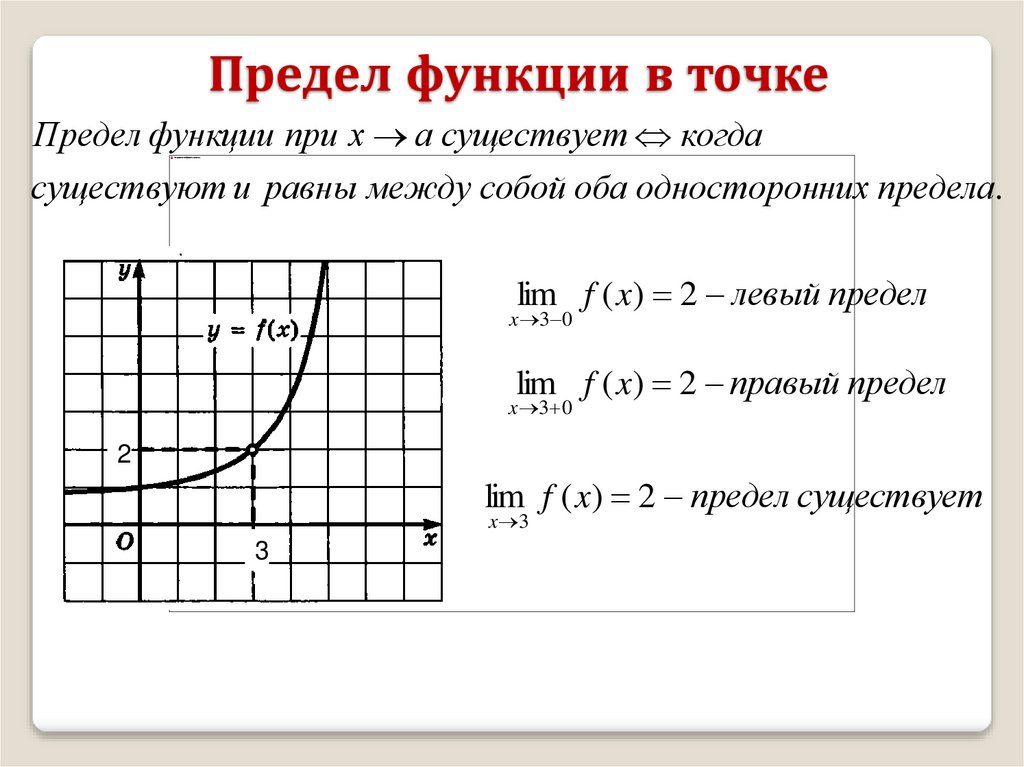
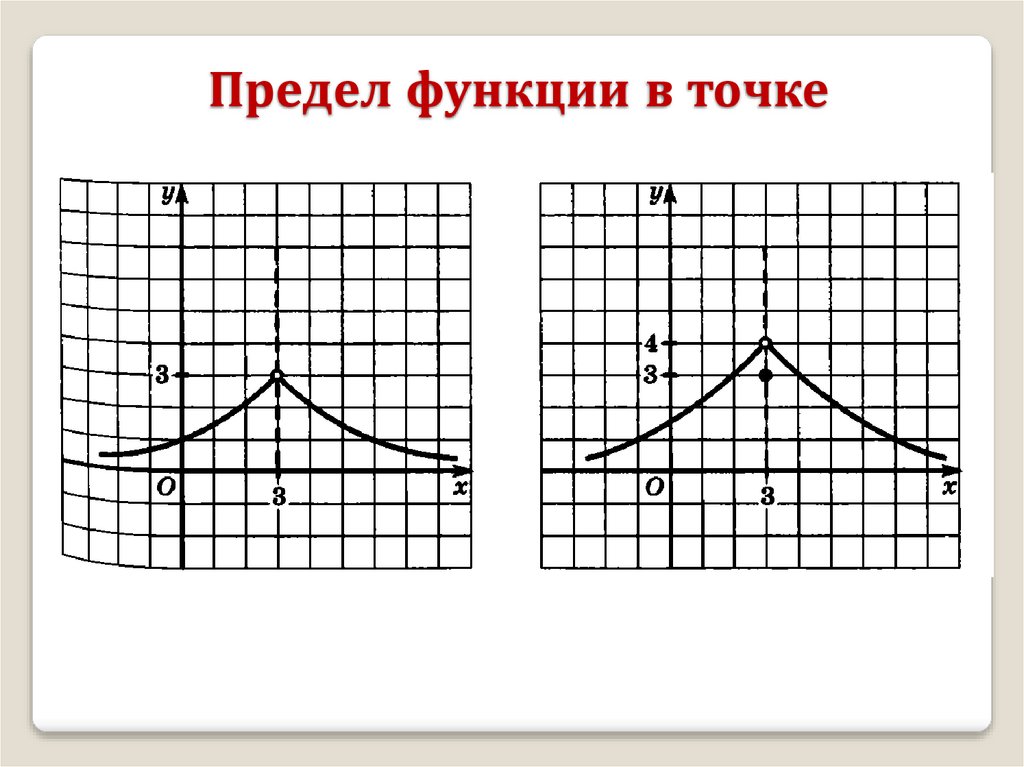
Предел функции в точке
Предел функции при х а существует когда
существуют и равны между собой оба односторонних предела.
lim f ( x) 2 левый предел
x 3 0
lim f ( x) 2 правый предел
x 3 0
2
lim f ( x) 2 предел существует
x 3
3

13.

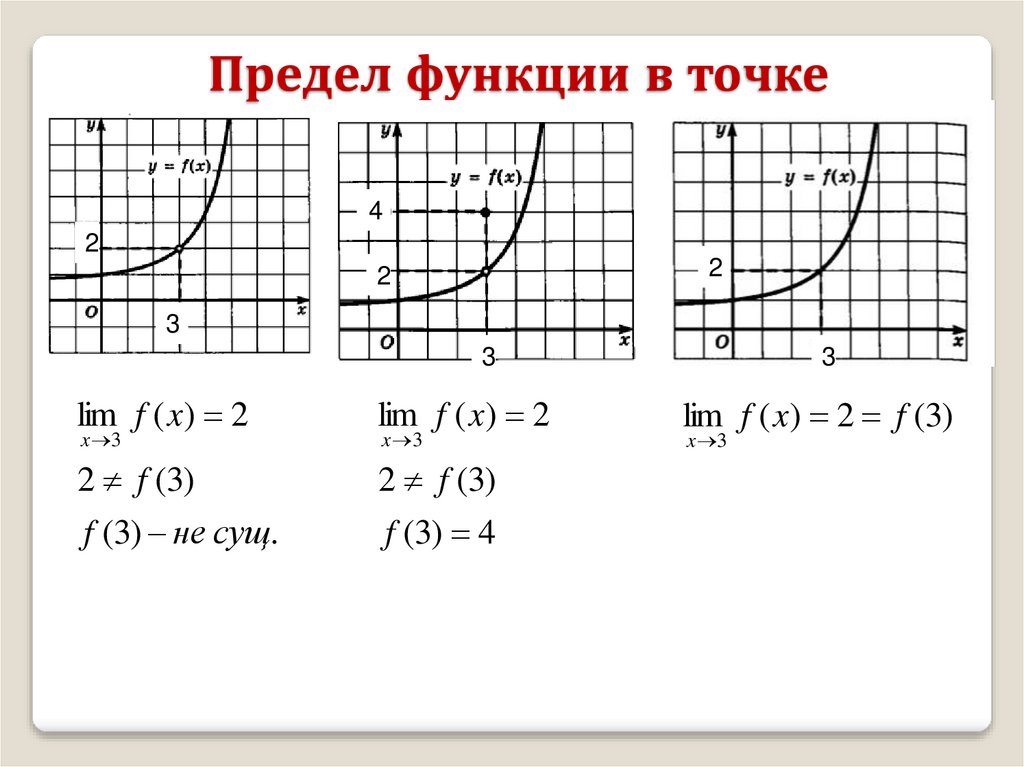
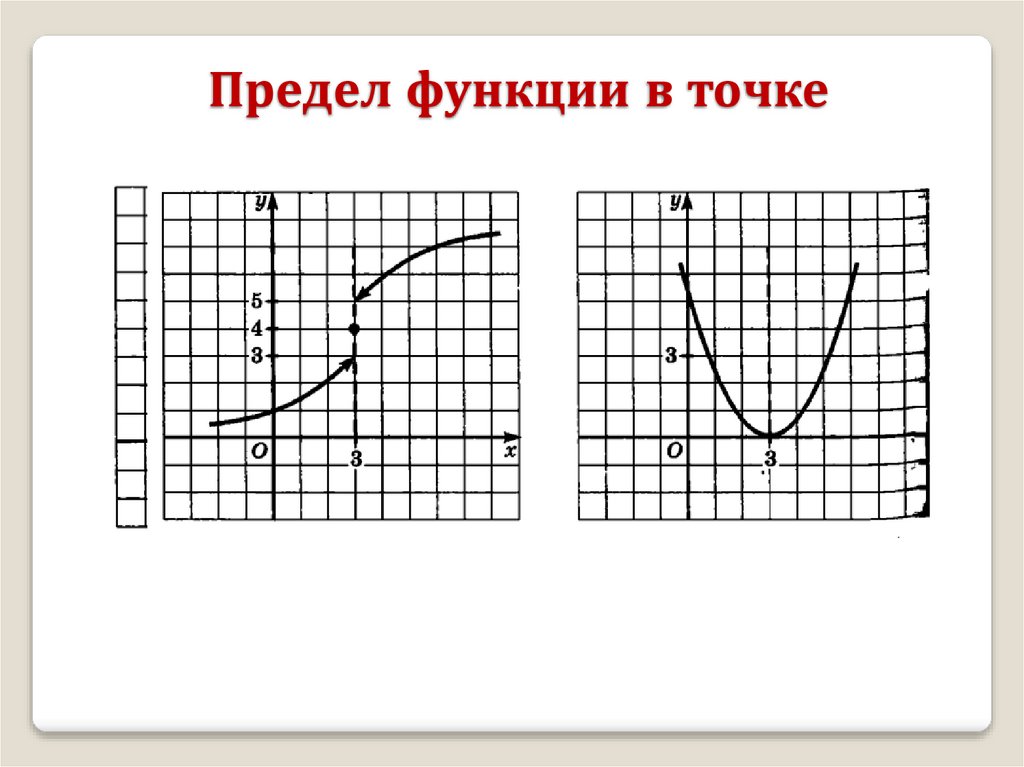
Предел функции в точке
4
2
2
2
3
3
lim f ( x) 2
lim f ( x) 2
2 f (3)
f (3) не сущ.
2 f (3)
x 3
x 3
f (3) 4
3
lim f ( x) 2 f (3)
x 3

14.

Предел функции

15.

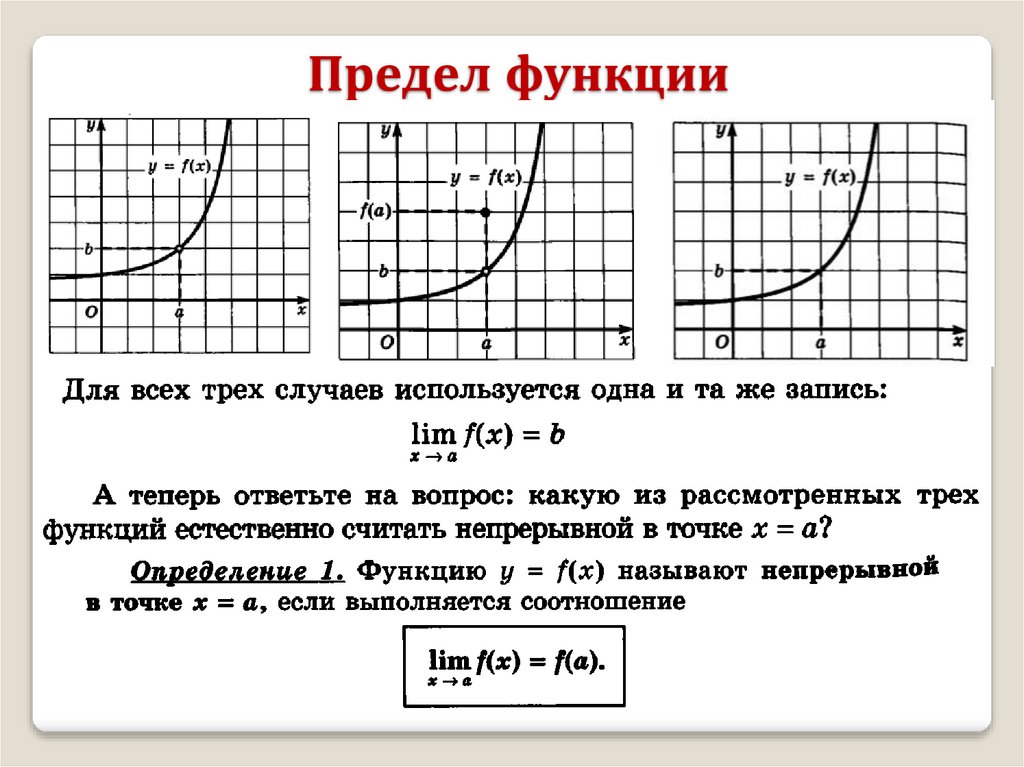
Предел функции в точке
Определение. Число А называется пределом функции f ( x)
в точке х а, если для любого 0 существует такое
число 0 , что для всех х, удовлетворяющих условию
0 x a выполняется неравенство f ( x) A .
А
а

16.

17.

Примеры

18.

Предел функции на
бесконечности
-3

19.

Предел функции в точке

20.

Предел функции в точке

21.

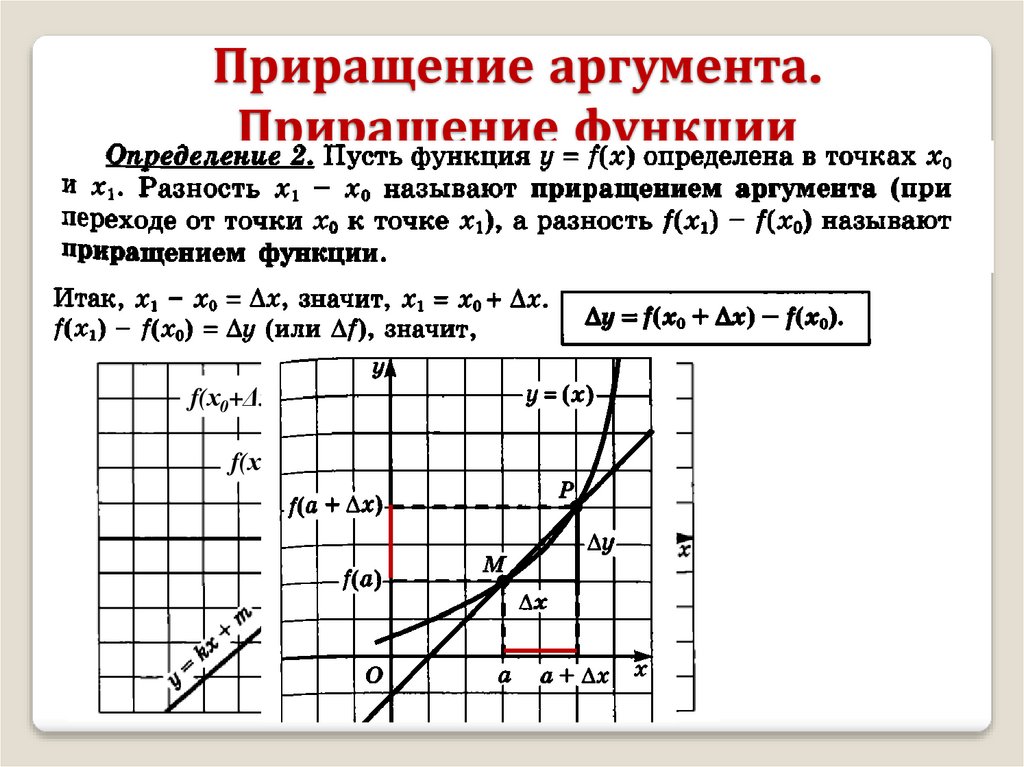
Приращение аргумента.
Приращение функции
f(х0+Δx)
f(х0)
х0
х0+Δх

22.

Определение производной
Если существует предел отношения
при х 0 ,
то этот предел называют производной функции у=f(x)
в точке х и обозначают f (x ) , т.е.

23.

Литература
Мордкович А.Г. Алгебра и начала математического анализа. 10 класс.
В 2 ч. Ч.1. Учебник для учащихся общеобразовательных учреждений
(профильный уровень) / А.Г. Мордкович, П.В. Семенов.- 9-е изд., стер.-
М.: Мнемозина, 2012.- 424 с.