1 дәріс буль функция

1.

КРИПТОГРАФИЯНЫҢ БУЛЬ
ФУНКЦИЯЛАРЫ

2.

Жоспары:
Буль функциялары
Комбинаторлық дәне алгебралық жолдары
Криптографиядағы буль функциялармен жұмыс істеу

3.

Буль функциялары көптеген криптографиялық алгоритмдердің негізгі құрылыс
блоктары болып табылады.
Криптографияда буль функциялар (немесе булев функциялар) — мәліметтерді
шифрлау мен қорғауда маңызды рөл атқаратын логикалық функциялар. Олар әдетте
шифрлау алгоритмдерінің тұрақтылығын, шифрланған мәліметтердің сенімділігін және
құпиялылықты қамтамасыз ету үшін қолданылады.
Буль функциялар — логикалық операцияларға негізделген, нәтижесі тек "0" және "1"
мәндерін қабылдайтын функциялар, олар биттік деңгейде шифрлау мен дешифрлау
процестерінде қолданылады.

4.

Криптографиядағы буль функциялардың
негізгі қолдану аймақтары:
1.Симметриялық блоктық шифрлар: Блоктық шифрлау алгоритмдерінде әрбір
блокты шифрлау немесе дешифрлау үшін буль функциялары қолданылады. Бұл
функциялар белгілі бір шарттарға сай таңдалып, деректердің сенімділігі мен қателікке
төзімділігін арттыруға көмектеседі.
2.Псевдо-қауіпсіз кілттер генерациясы: Буль функциялары криптографияда
кездейсоқтық элементтерін енгізуге көмектеседі, соның арқасында шифрланған
мәтіндер бірегей және қауіпсіз болып табылады.
3.Шифрлау алгоритмдерінің күрделілігін арттыру: Буль функциялардың көмегімен
криптографиялық алгоритмдердегі қадамдар санын арттыруға және шифрды
анализдеуді қиындатуға болады. Бұл алгоритмдердің сызықтылығын азайтып, күрделі
математикалық әдістердің қолданылуын қамтамасыз етеді.

5.

Криптографияда булев функцияларының маңызды ерекшеліктері
бар. Олардың негізгілері:
1. Сызықтық емес – булев функцияның негізгі криптографиялық тұрақтылық көрсеткіштерінің
бірі. Функция неғұрлым сызықсыз болса, оны сызықтық тәсілдермен немесе қарапайым
алгебралық амалдармен шешу соғұрлым қиынға соғады. Сызықтық емес функциялар
криптографиялық жүйелерде ақпаратты сенімді қорғауға мүмкіндік береді.
Мысалы: DES және AES сияқты блоктық шифрларда S-блоктар сызықсыз түрлендірулерді
орындайды. Бұл шифрды криптоанализге төзімді етеді.
2. Теңдестірілгендік
Булев функция теңдестірілген деп аталады, егер оның шығыс мәндерінің саны теңдей 0 және 1
мәндерін қабылдаса. Бұл криптографиялық функцияларда кездейсоқтықты қамтамасыз ету
үшін маңызды.
Мысалы: Егер булев функция теңдестірілмесе, онда ол шифрланған деректерді талдауға оңай
жол ашады, себебі кейбір мәндер басқаларына қарағанда жиі кездеседі.

6.

Криптографияда булев функцияларының маңызды ерекшеліктері бар. Олардың
негізгілері:
3. Корреляциялық иммунитет булев функцияның кірістер арасындағы байланыстарды азайту қабілетімен
анықталады. Бұл қасиет әсіресе корреляциялық шабуылдарға қарсы маңызды.
Мысалы: Ағынды шифрларда булев функциялар жоғары корреляциялық иммунитетке ие болса, кілтті талдау
қиындайды.
4. Бент-функциялар — максималды сызықсыздыққа ие арнайы булев функциялар класы. Олар ең жақсы
криптографиялық қасиеттерді көрсетеді, бірақ тек жұп саны бар кіріс айнымалылармен қолданылады. Бентфункциялар сызықсыздық пен тұрақтылықтың жоғары деңгейін қамтамасыз етіп, күрделі криптографиялық
жүйелерде қолданылады.
Мысалы: Бент-функциялар S-блоктар немесе кілт генераторлары сияқты криптографиялық компоненттерді
жобалауда қолданылады.
5. Лавиндік эффект
Булев функциялар лавиндік эффектті қамтамасыз ету үшін де қолданылады. Лавиндік эффект криптографияда
өте маңызды, себебі ол шабуылшыларға бастапқы деректерді болжауға мүмкіндік бермейді.
Мысалы: SHA-256 хеш-функциясында лавиндік эффект үлкен рөл атқарады, себебі бастапқы деректің ең
кішкентай өзгерісі хеш нәтижесінде үлкен өзгеріс тудырады.

7.

Булев амалдар криптографияда деректерді шифрлау және түрлендіру кезінде кеңінен
қолданылады. Әрбір булев амал шифрлау алгоритмдерінде маңызды рөл атқарып,
деректерді өңдеу мен шифрлау тұрақтылығын қамтамасыз етеді.
Төменде криптографияда қолданылатын негізгі булев амалдар және олардың рөлі
сипатталған.
3
2
1
Логикалық ЖӘНЕ (AND)
Логикалық НЕМЕСЕ (OR)
4
Логикалық ЕМЕС (NOT)
3
Логикалық ЕМЕС (NOT)
Логикалық ЕМЕС (NOT)

8.

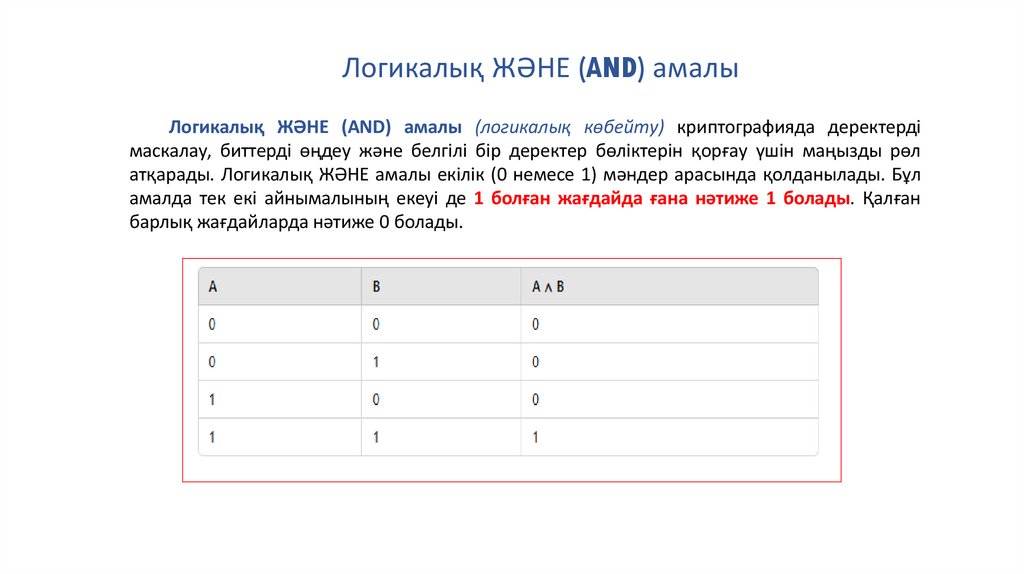
Логикалық ЖӘНЕ (AND) амалы
Логикалық ЖӘНЕ (AND) амалы (логикалық көбейту) криптографияда деректерді
маскалау, биттерді өңдеу және белгілі бір деректер бөліктерін қорғау үшін маңызды рөл
атқарады. Логикалық ЖӘНЕ амалы екілік (0 немесе 1) мәндер арасында қолданылады. Бұл
амалда тек екі айнымалының екеуі де 1 болған жағдайда ғана нәтиже 1 болады. Қалған
барлық жағдайларда нәтиже 0 болады.

9.

Логикалық ЖӘНЕ (AND) амалы
Негізгі қолдану салалары
Биттік маскалау — бұл ЖӘНЕ амалы арқылы белгілі бір биттерді таңдап алу немесе кейбір
биттерді жасырып қою әдісі. Маскалау криптографияда деректердің немесе кілттің кейбір бөліктерін
"жасырып", қорғалған түрде көрсету үшін қолданылады.
Мысал: Егер бастапқы дерек 1011 1101, ал маска 1111 0000 болса, маскалау нәтижесінде дерек
1011 0000 болады.
1011 1101
*
1111 0000
_________
1011 0000

10.

Кілтті қорғау және сақтауда қолдану
Криптографиялық алгоритмдерде ЖӘНЕ амалы құпия кілттің кейбір бөліктерін сақтау
немесе қорғау мақсатында пайдаланылады. Бұл кезде бастапқы дерек пен кілт арасында ЖӘНЕ
амалы орындалады, осылайша белгілі биттер ғана өңдеуге қатысады.
Мысал:
Бастапқы дерек: 1110 1010
Құпия кілт: 1011 1100
ЖӘНЕ амалы орындалғаннан кейін нәтиже 1010 1000 болады.
1110
1010
*
1011 1100
_________
1010 1000

11.

Деректерді бөліп алу немесе белгілі биттерді таңдау
Логикалық ЖӘНЕ амалы белгілі биттерді бөліп алу немесе деректерді бөліп сақтау
мақсатында қолданылады. Бұл амал арқылы деректердің қажетсіз бөліктерін жоюға немесе тек
маңызды биттерді сақтап қалуға болады.
Мысал:
Бастапқы дерек: 1101 1010
Құпия кілт: 1111 0000
ЖӘНЕ амалы орындалғаннан кейін нәтиже 1101 0000 болады.
* 1101 1010
1111
0000
_________
1101 0000
Бұл әдіс деректердің маңызды бөлігін бөліп алып, қажетсіз бөліктерін шифрлауға
қатыстырмау үшін тиімді.

12.

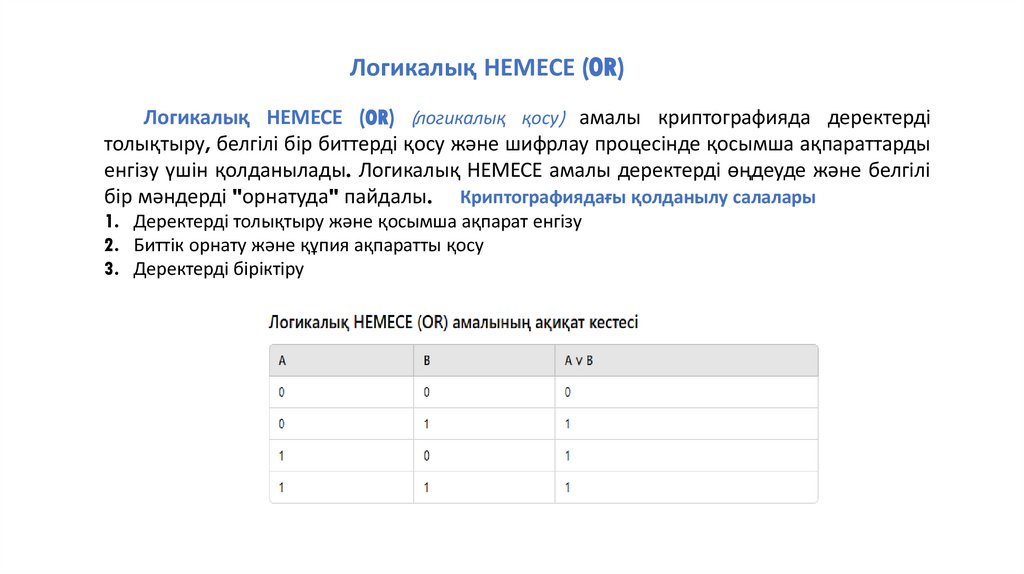
Логикалық НЕМЕСЕ (OR)
Логикалық НЕМЕСЕ (OR) (логикалық қосу) амалы криптографияда деректерді
толықтыру, белгілі бір биттерді қосу және шифрлау процесінде қосымша ақпараттарды
енгізу үшін қолданылады. Логикалық НЕМЕСЕ амалы деректерді өңдеуде және белгілі
бір мәндерді "орнатуда" пайдалы. Криптографиядағы қолданылу салалары
1. Деректерді толықтыру және қосымша ақпарат енгізу
2. Биттік орнату және құпия ақпаратты қосу
3. Деректерді біріктіру

13.

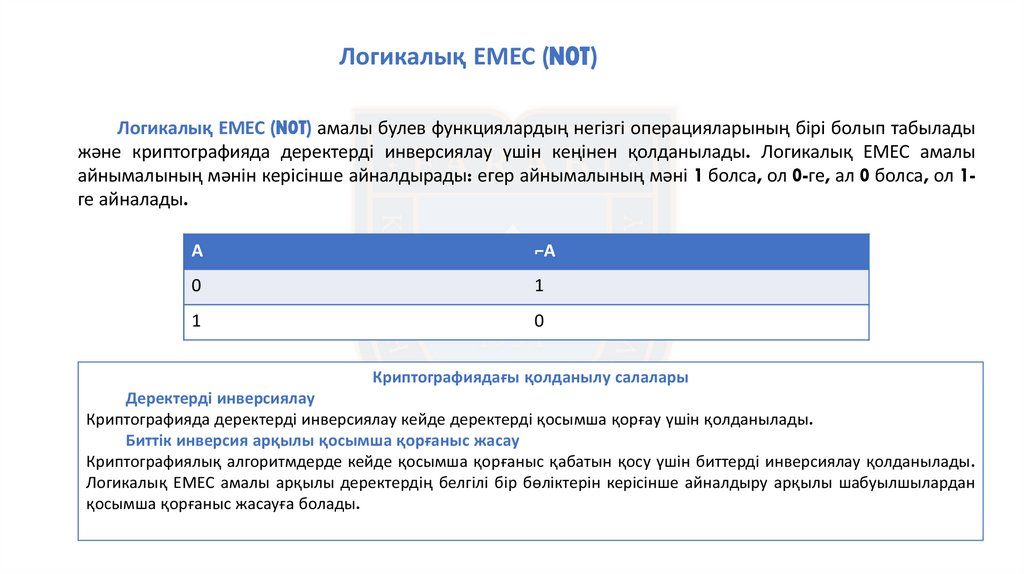
Логикалық ЕМЕС (NOT)
Логикалық ЕМЕС (NOT) амалы булев функциялардың негізгі операцияларының бірі болып табылады
және криптографияда деректерді инверсиялау үшін кеңінен қолданылады. Логикалық ЕМЕС амалы
айнымалының мәнін керісінше айналдырады: егер айнымалының мәні 1 болса, ол 0-ге, ал 0 болса, ол 1ге айналады.
А
⌐А
0
1
1
0
Криптографиядағы қолданылу салалары
Деректерді инверсиялау
Криптографияда деректерді инверсиялау кейде деректерді қосымша қорғау үшін қолданылады.
Биттік инверсия арқылы қосымша қорғаныс жасау
Криптографиялық алгоритмдерде кейде қосымша қорғаныс қабатын қосу үшін биттерді инверсиялау қолданылады.
Логикалық ЕМЕС амалы арқылы деректердің белгілі бір бөліктерін керісінше айналдыру арқылы шабуылшылардан
қосымша қорғаныс жасауға болады.