Lection_06

1. 3. Ранг матрицы

Элементы линейной алгебры
3. Ранг матрицы

2. Ранг матрицы (1)

Рассмотрим матрицу
a11
a 21
A
....
a
m1
a12
a 22
....
am2
.... a1n
.... a 2 n
..... .....
..... a mn
Минором к – го порядка матрицы А
называется определитель к – го порядка
с элементами, стоящими на пересечении
любых к строк и к столбцов.
(k min m, n )

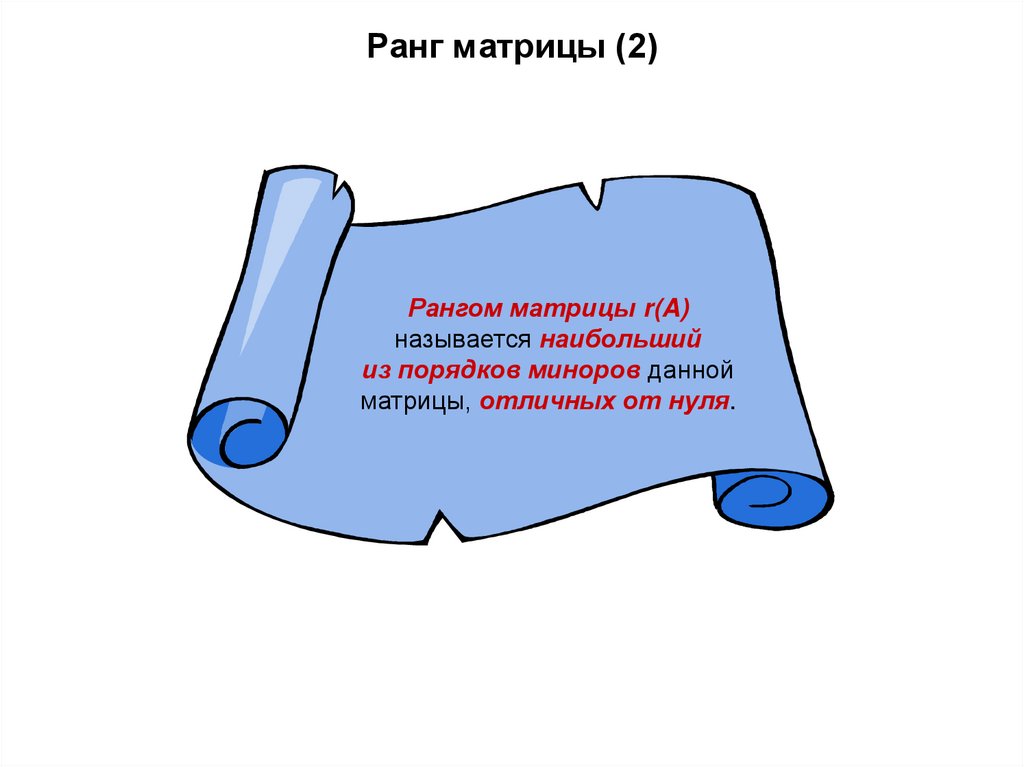
3. Ранг матрицы (2)

Рангом матрицы r(A)
называется наибольший
из порядков миноров данной
матрицы, отличных от нуля.

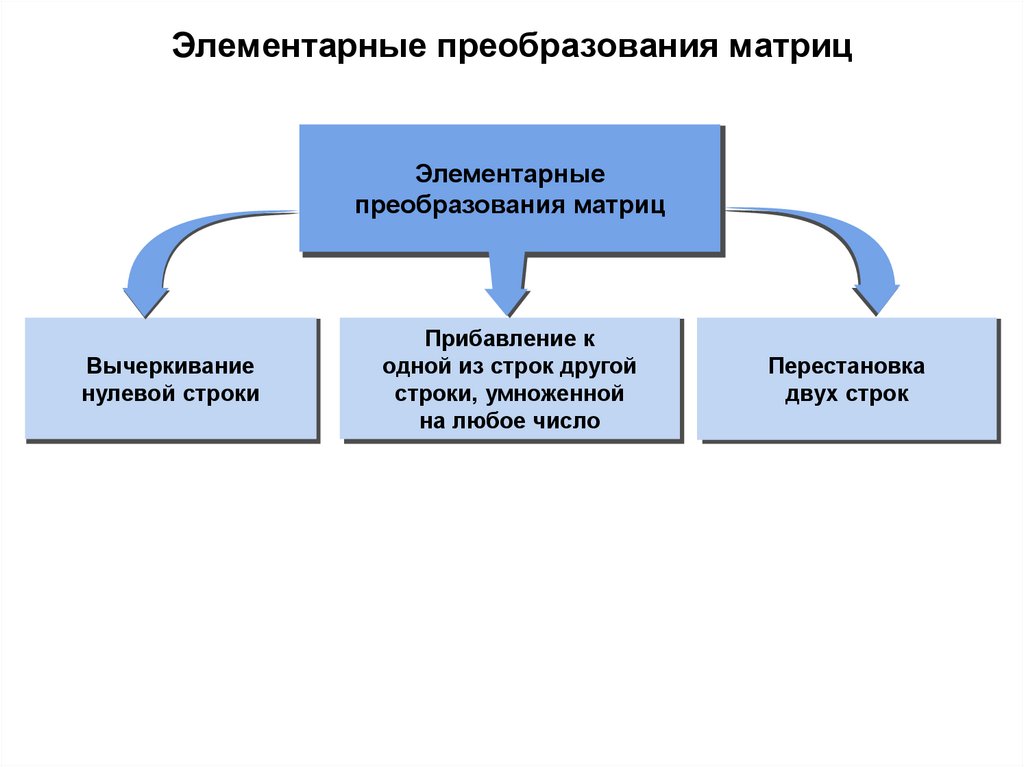
4. Элементарные преобразования матриц

Элементарные
преобразования матриц
Вычеркивание
нулевой строки
Прибавление к
одной из строк другой
строки, умноженной
на любое число
Перестановка
двух строк

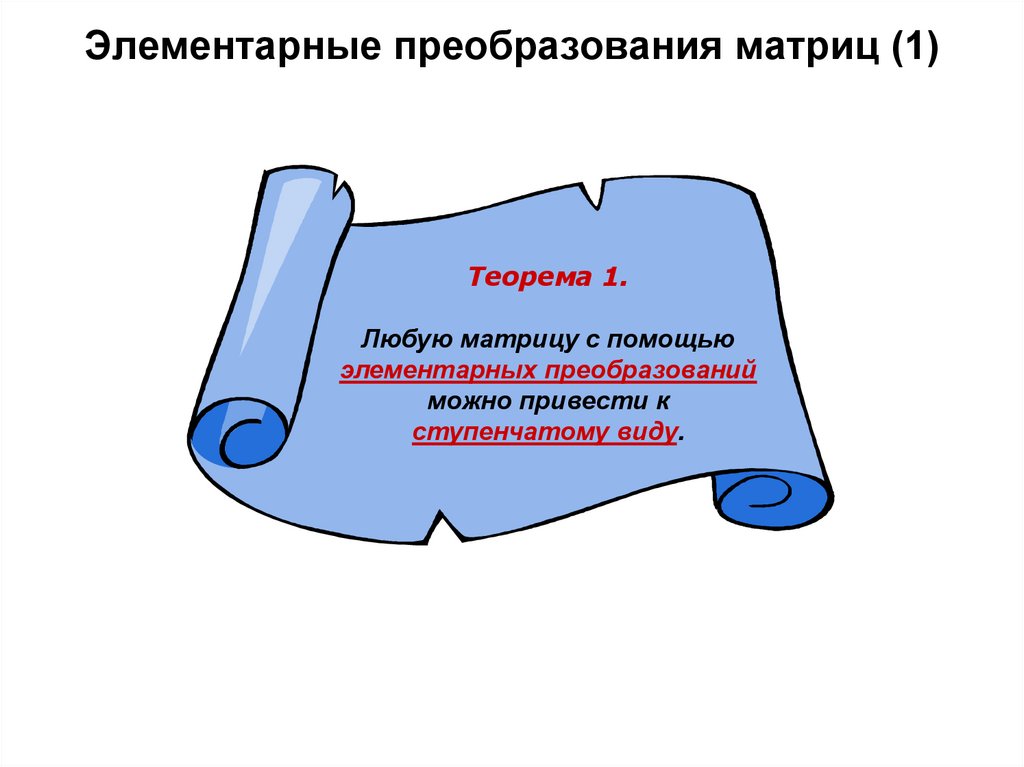
5. Элементарные преобразования матриц (1)

Теорема 1.
Любую матрицу с помощью
элементарных преобразований
можно привести к
ступенчатому виду.

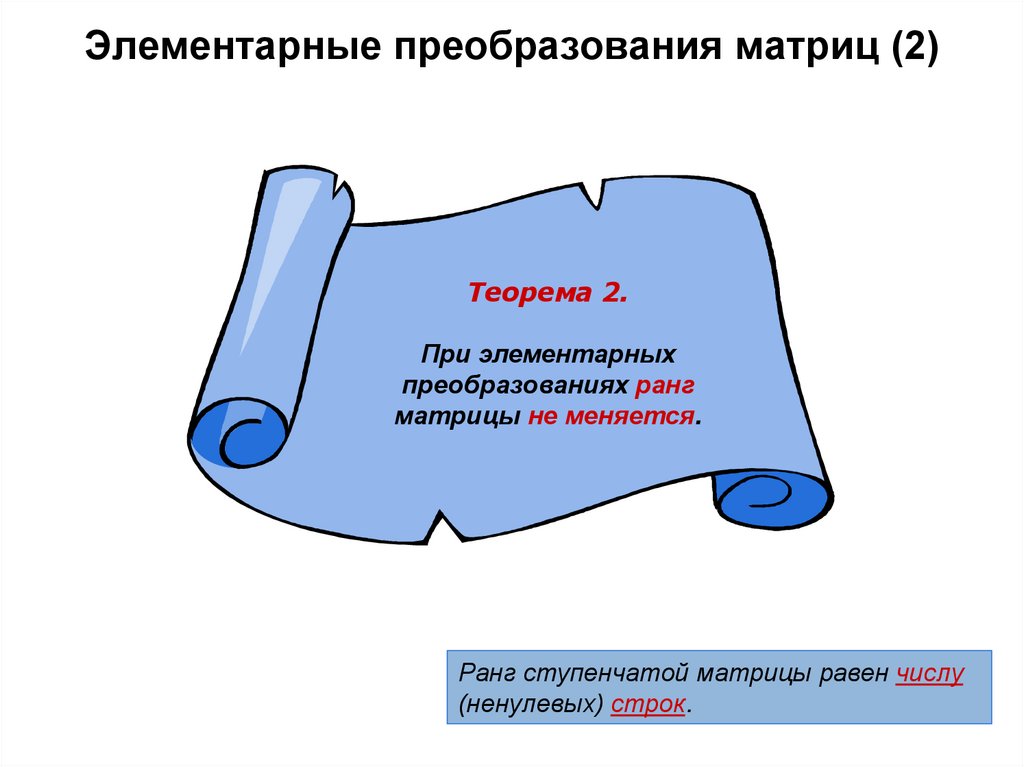
6. Элементарные преобразования матриц (2)

Теорема 2.
При элементарных
преобразованиях ранг
матрицы не меняется.
Ранг ступенчатой матрицы равен числу
(ненулевых) строк.

7. Пример 6 (1)

Найти ранг матрицы:
1 -3 -1
A= 2 1 4 .
3 -2 3

8. Пример 6 (2)

Решение. Приведем матрицу к ступенчатому виду:
1 -3 -1 ·(-2)
↓
2 1 4 ←
3 -2 3

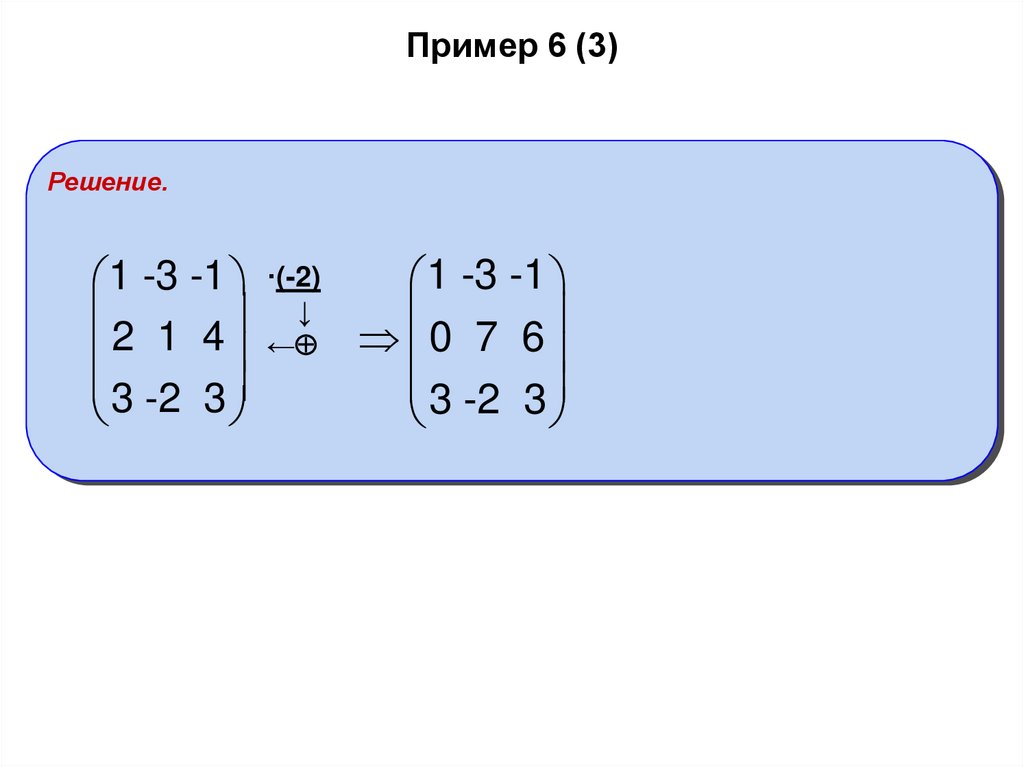
9. Пример 6 (3)

Решение.
1 -3 -1
1 -3 -1 ·(-2)
↓
2
1
4
0
7
6
←
3 -2 3
3 -2 3

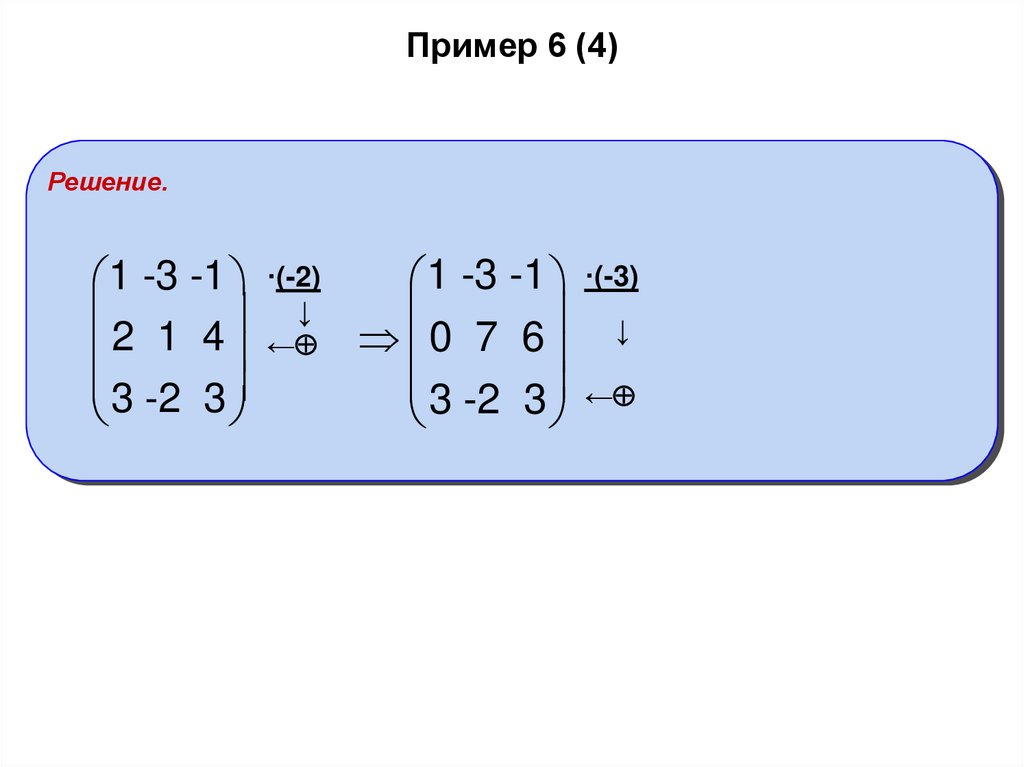
10. Пример 6 (4)

Решение.
1 -3 -1 ·(-3)
1 -3 -1 ·(-2)
↓
↓
2
1
4
0
7
6
←
3 -2 3
3 -2 3 ←

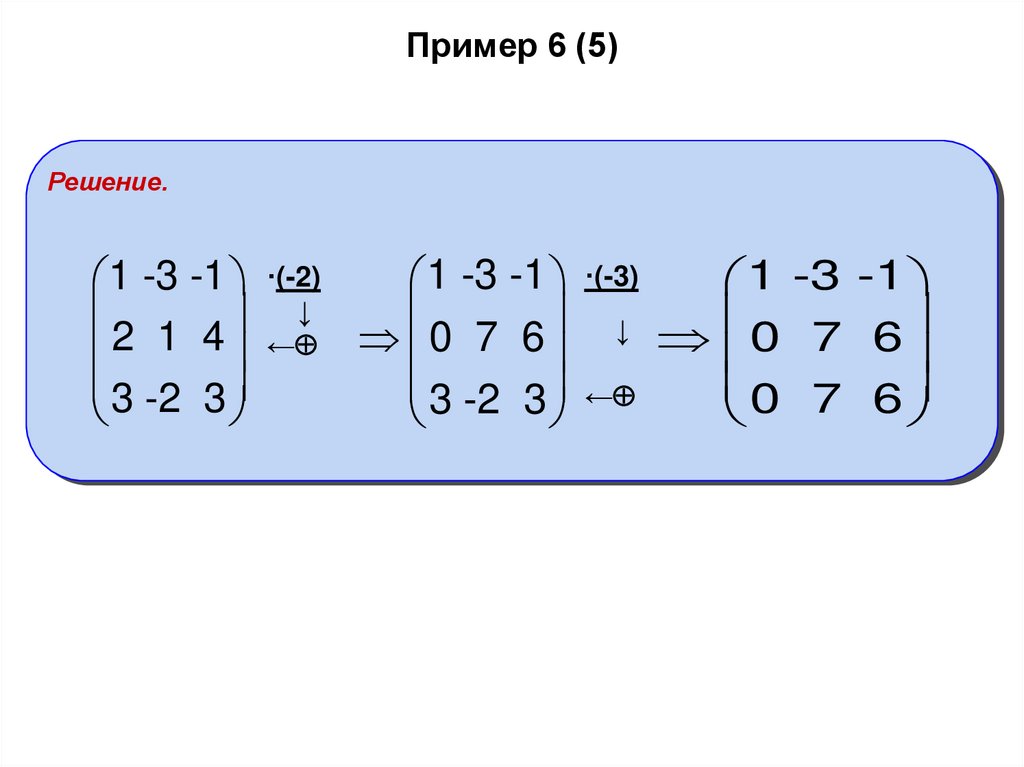
11. Пример 6 (5)

Решение.
1 -3 -1 ·(-3)
1 -3 -1 ·(-2)
1 -3 -1
↓
↓
2
1
4
0
7
6
0
7
6
←
3 -2 3
0 7 6
3 -2 3 ←

12. Пример 6 (6)

Решение.
1 -3 -1
1 -3 -1
·(-1) 0 7 6
0
7
6
↓
0 0 0
0 7 6
←

13. Пример 6 (7)

Решение.
1 -3 -1
1 -3 -1
1 -3 -1
·(-1) 0 7 6
0 7 6
0 7 6 ↓
0 0 0
0 7 6
←
r(A)=2

14. 4. Метод Гаусса

15. Метод Гаусса (1)

Метод последовательного
исключения неизвестных –
наиболее распространенный
метод решения систем
линейных уравнений.

16. Метод Гаусса (2)

Рассмотрим систему
a11 x1 a12 x2 ... a1n xn b1
a x a x ... a x b
21 1
22 2
2n n
2
...............................................
a m1 x1 a m 2 x2 ... a m n xn bm

17. Метод Гаусса (3)

Рассмотрим систему
a11 x1 a12 x2 ... a1n xn b1
a x a x ... a x b
21 1
22 2
2n n
2
...............................................
a m1 x1 a m 2 x2 ... a m n xn bm
С помощью элементарных преобразований
приводим ее к равносильной системе ступенчатого вида:
c11x1 c12 x2 c1n xn d1
c22 x2 c2 n xn d 2
...............................................
ckr xr ... ckn xn d k

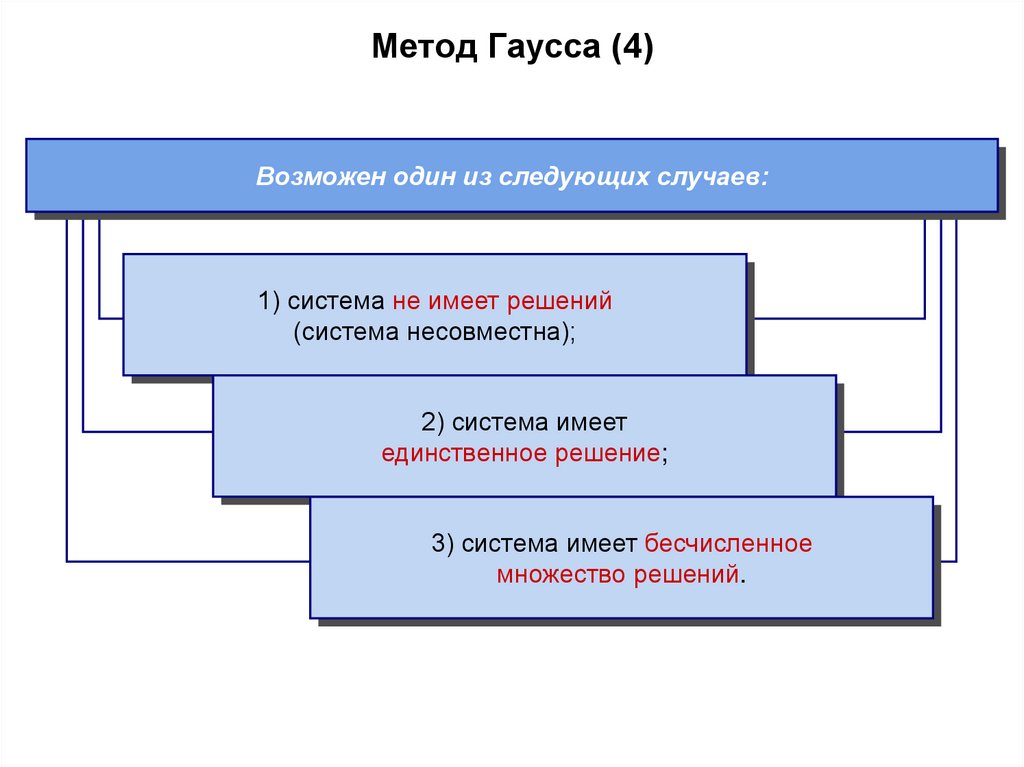
18. Метод Гаусса (4)

Возможен один из следующих случаев:
1) система не имеет решений
(система несовместна);
2) система имеет
единственное решение;
3) система имеет бесчисленное
множество решений.

19. Теорема Кронекера-Капелли (1)

Рассмотрим систему уравнений
a11 x1 a12 x2 ... a1n xn b1
a x a x ... a x b
21 1
22 2
2n n
2
...............................................
a m1 x1 a m 2 x2 ... a m n xn bm

20. Теорема Кронекера-Капелли (2)

Рассмотрим систему уравнений
a11 x1 a12 x2 ... a1n xn b1
a x a x ... a x b
21 1
22 2
2n n
2
...............................................
a m1 x1 a m 2 x2 ... a m n xn bm
Обозначим
a11
a 21
A
....
a
m1
a12
a 22
....
am2
.... a1n
.... a 2 n
..... .....
..... a mn
a11
~ a21
A
....
am1
a12
a22
....
am 2
a1n b1
a2 n b2
.....
.....
..... amn b
m
....
....

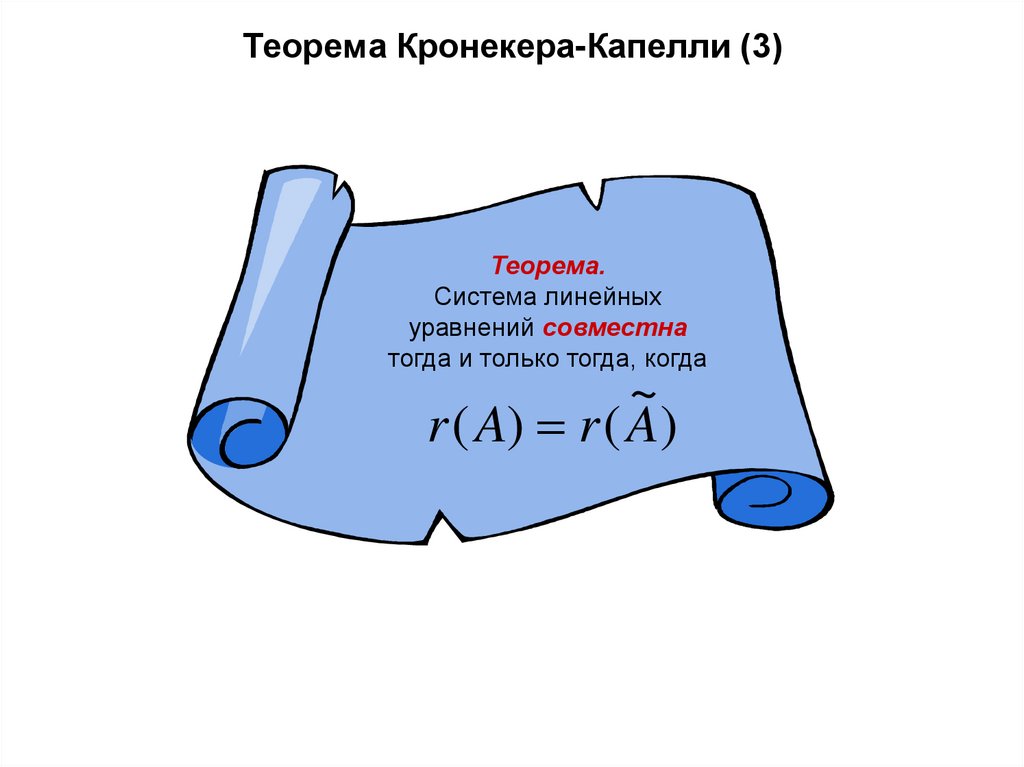
21. Теорема Кронекера-Капелли (3)

Теорема.
Система линейных
уравнений совместна
тогда и только тогда, когда
~
r ( A) r ( A)

22. Пример 7 (1)

Методом Гаусса решить систему уравнений:
x1 2 x2 2 x3 3
2 x1 3x2 2 x3 5
x 3x 1
3
2

23. Пример 7 (2)

Решение. Запишем расширенную матрицу:
x1 2 x2 2 x3 3
2 x1 3x2 2 x3 5
x 3x 1
3
2
1 2 2 3
2 3 2 5
0 1 3 1

24. Пример 7 (3)

Решение. Приведем расширенную матрицу к ступенчатому виду:
1 2 2 3 ·(-2)
↓
2 3 2 5 ←
0 1 3 1
1 2 2 3
0 1 2 1
0 1 3 1

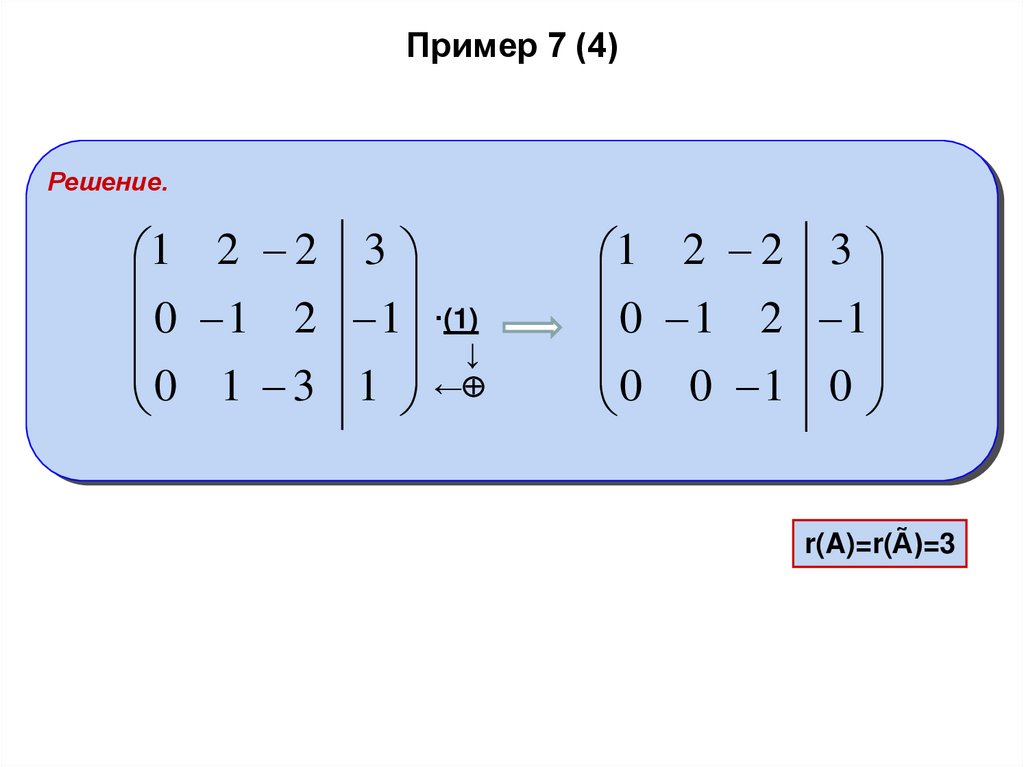
25. Пример 7 (4)

Решение.
1 2 2 3
0 1 2 1 ·(1)↓
0 1 3 1 ←
1 2 2 3
0 1 2 1
0 0 1 0

26. Пример 7 (4)

Решение.
1 2 2 3
0 1 2 1 ·(1)↓
0 1 3 1 ←
1 2 2 3
0 1 2 1
0 0 1 0
r(A)=r(Ã)=3

27. Пример 7 (5)

Решение.
1 2 2 3
0 1 2 1
0 0 1 0
x1 2 x2 2 x3 3
x2 2 x3 1
x3 0 x3 0

28. Пример 7 (6)

Решение.
x1 2 x2 2 0 3
x2 2 0 1
x2 1

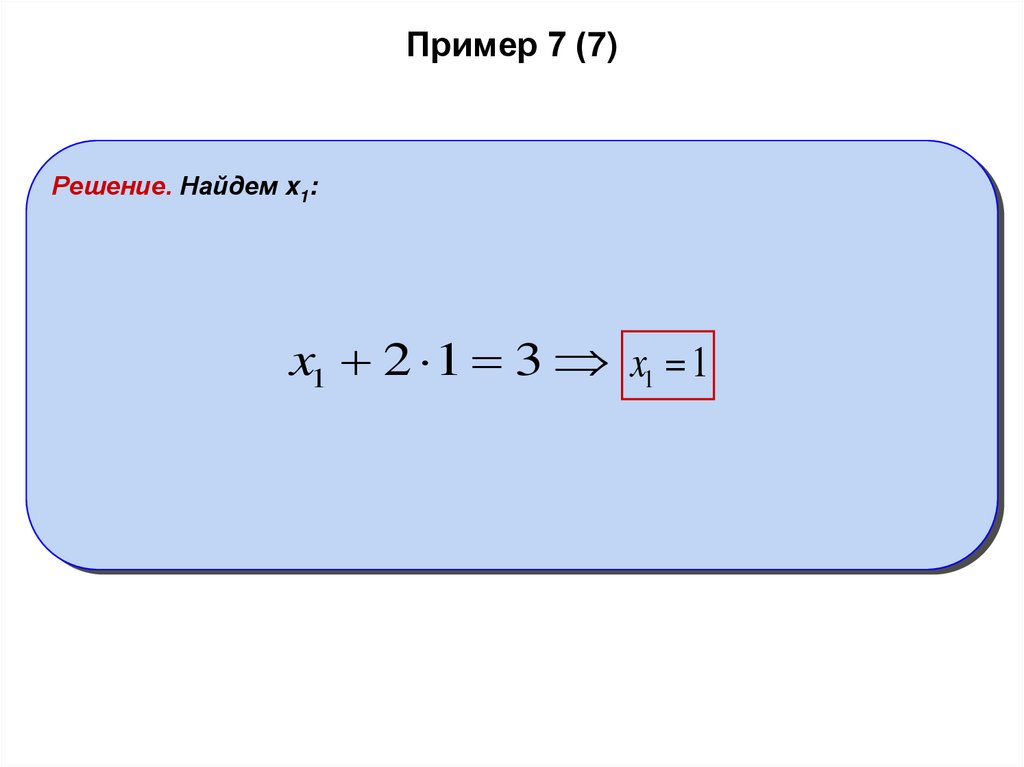
29. Пример 7 (7)

Решение. Найдем x1:
x1 2 1 3 x1 1

30. Пример 7 (8)

Решение.
x1=1, x2=1, x3=0 – единственное решение.

31. Окончание лекции