24.01.26_Преобразование графиков тригонометрических функций (1)

1. Преобразование графиков тригонометрических функций

ТЕМА УРОКА:
ПРЕОБРАЗОВАНИЕ ГРАФИКОВ
ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ

2.

РЕБЯТА, ЗАПИСЫВАЕМ ТЕМУ УРОКА. ЧЕРТИМ В ТЕТРАДЬ КАРАНДАШОМ
ГРАФИКИ, РАСПОЛОЖЕННЫЕ НА СЛЕДУЮЩИХ СЛАЙДАХ : 4, 6, 7, 8
С СООТВЕТСТВУЮЩИМИ ЗАПИСЯМИ НА СЛАЙДЕ.
ГРАФИКИ ПРОВЕРЮ НА ОЧНОМ УРОКЕ. ПО ВОЗМОЖНОСТИ ГРАФИКИ ВЫДЕЛЯЙТЕ
ЦВЕТНЫМИ КАРАНДАШАМИ, ЕСЛИ ИХ НЕТ, ТО Я ВАМ ИХ ДАМ В КОЛЛЕДЖЕ , ОБВЕДЕТЕ
ПОТОМ.
ЧЕРТИТЕ ПРАВИЛЬНО, ПЛАВНО, АККУРАТНО, БЕЗ ГРЯЗИ.

3. Содержание

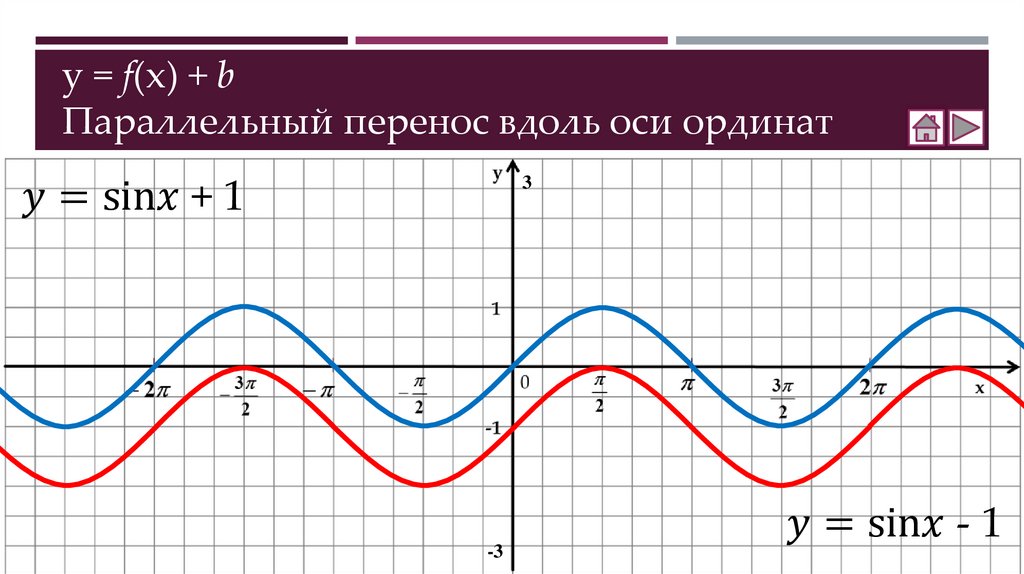
Теория
Как построить график функции y = f(x) + b
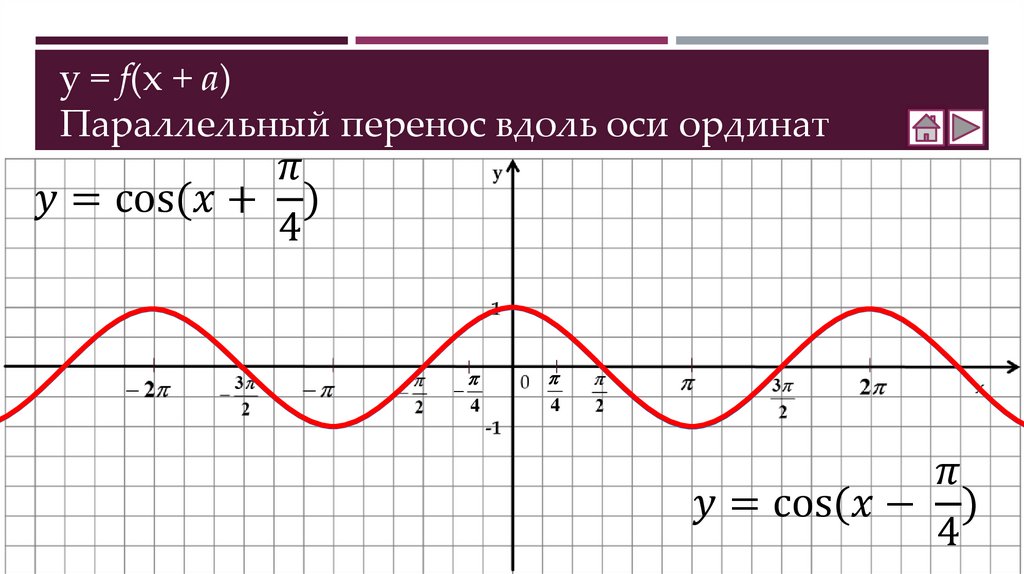
Как построить график функции y = f(x + a)
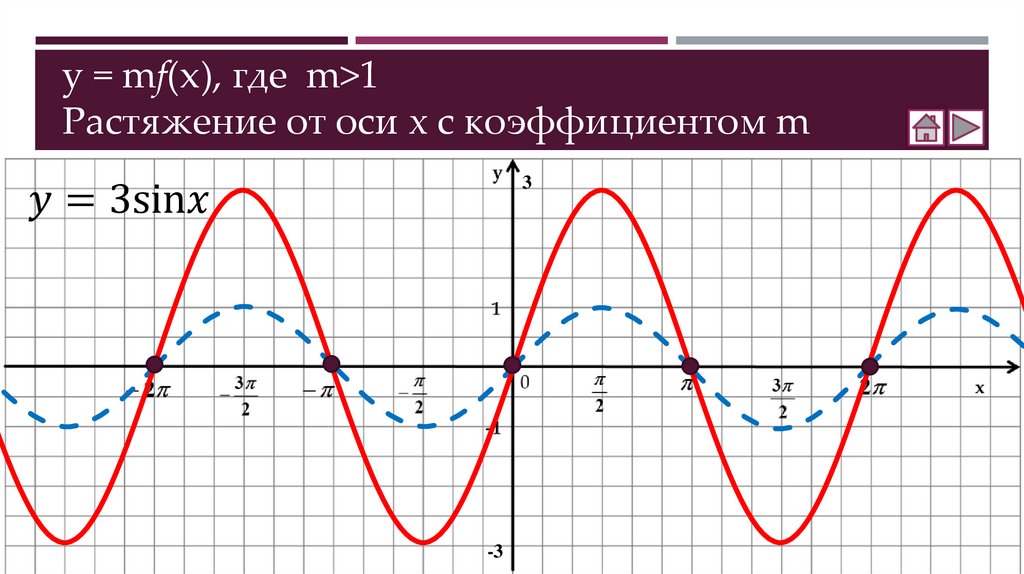
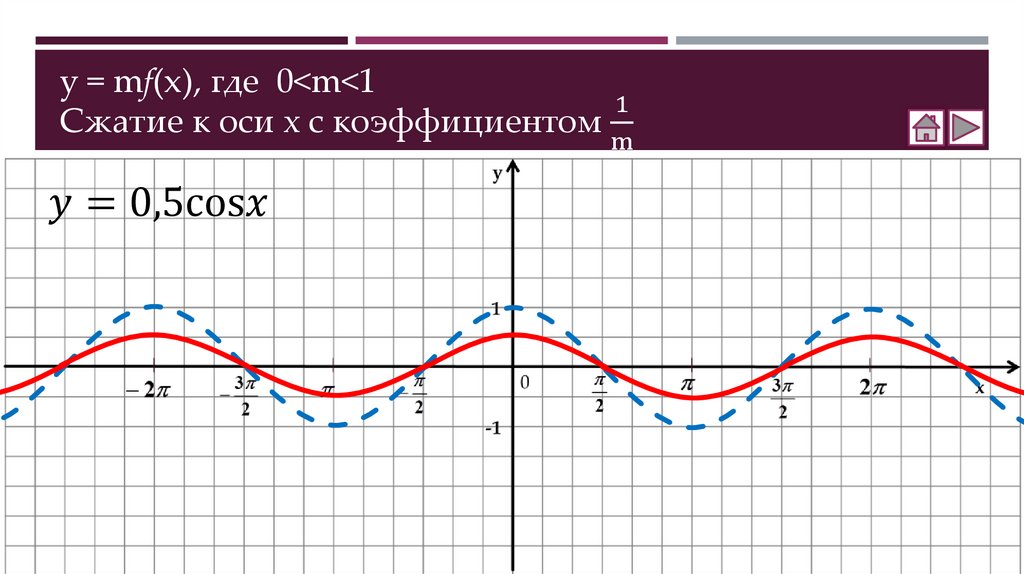
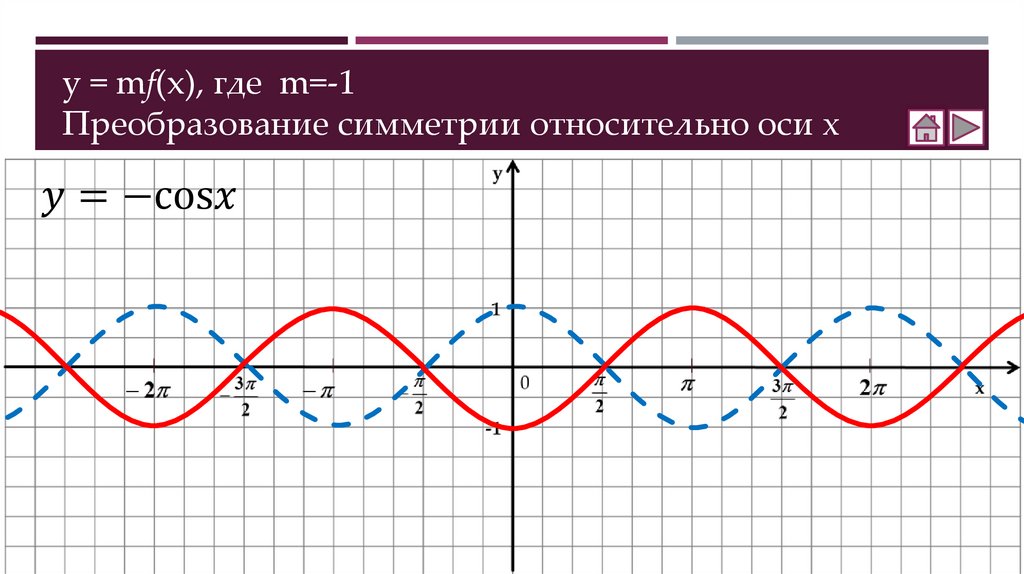
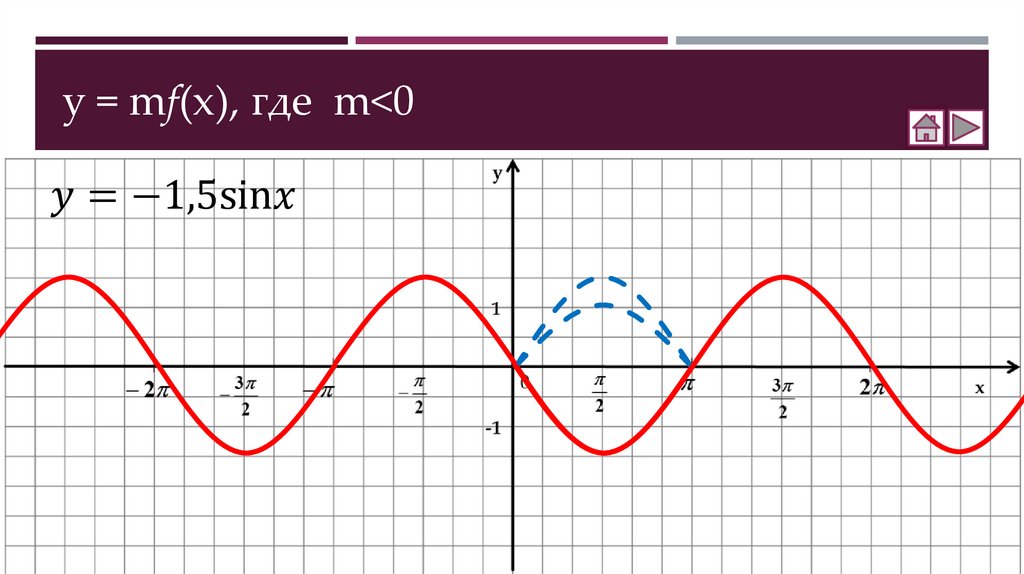
Как построить график функции y = mf(x)
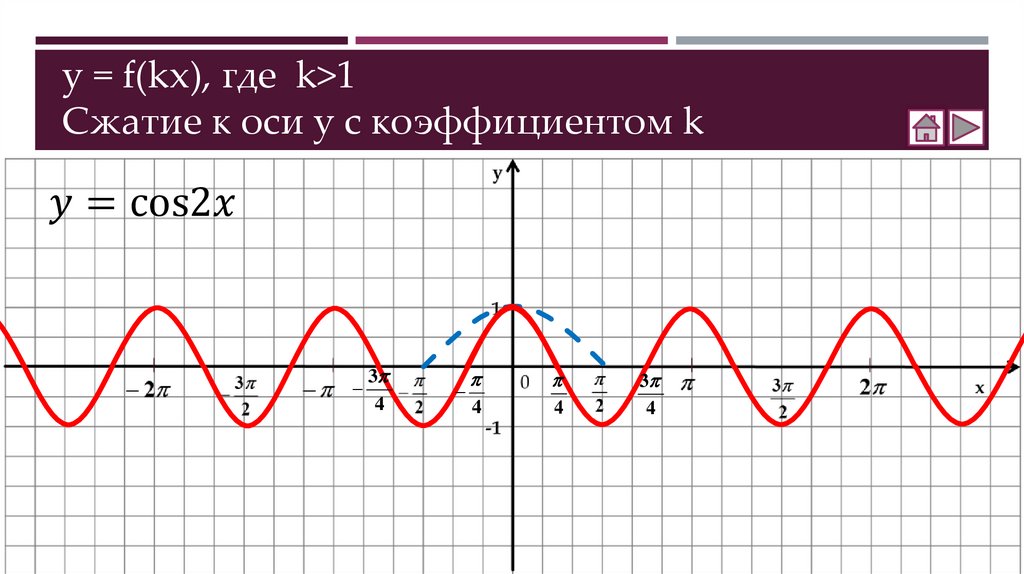
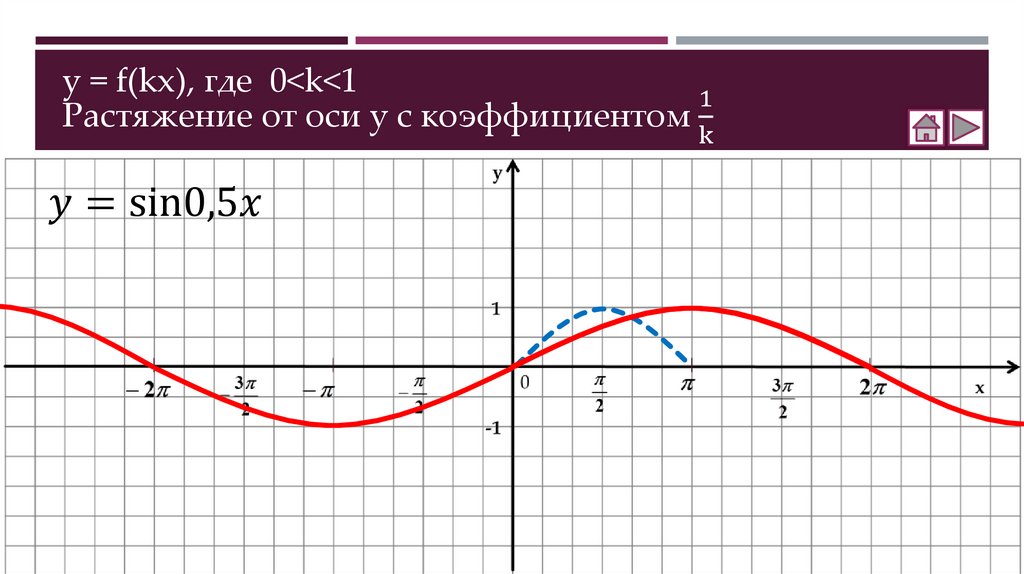
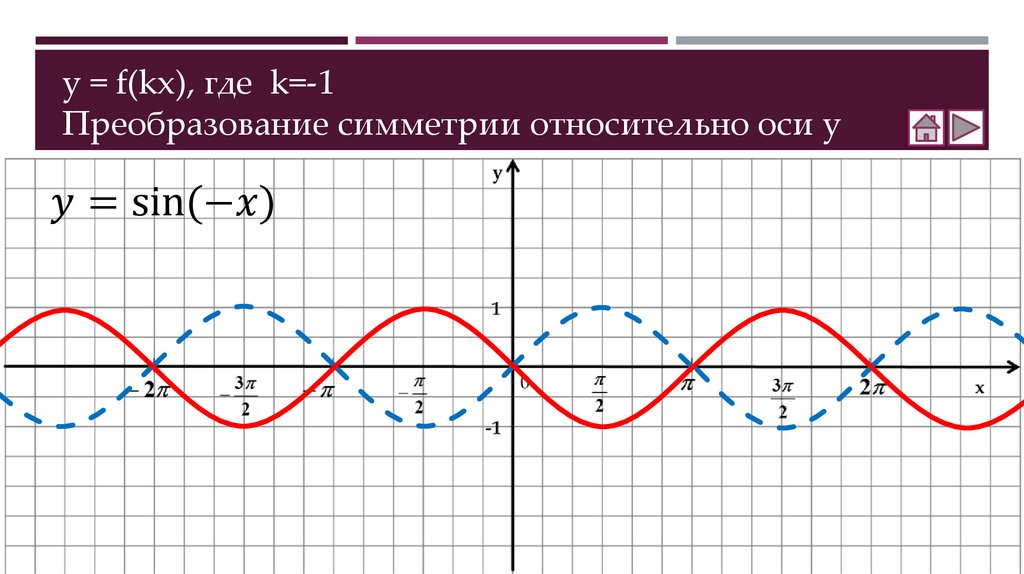
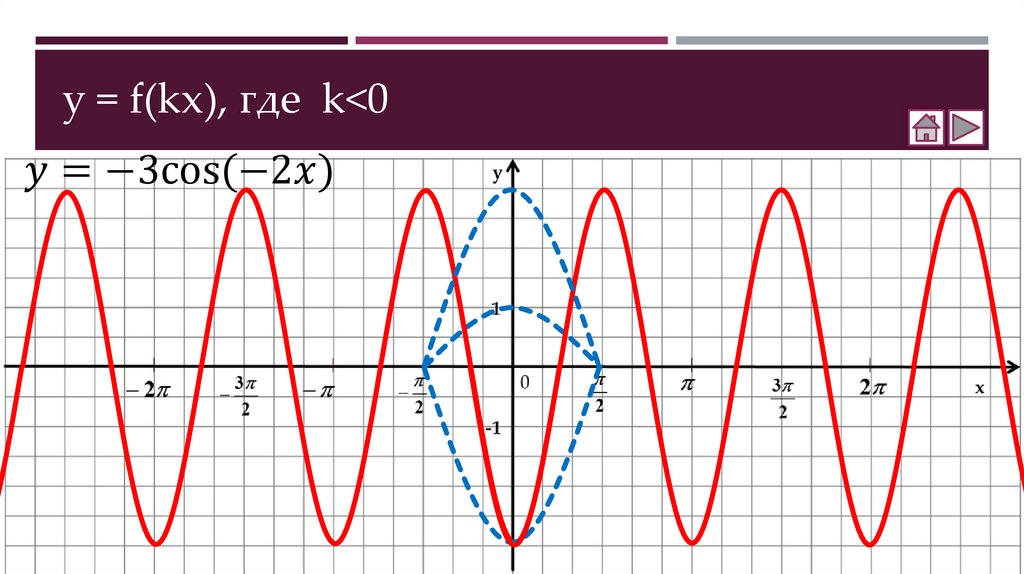
Как построить график функции y = f(kx)
Практика
Соотнесение графиков функций с их формулами
Построение графиков функций
Составление аналитической записи функции по её графику
Самостоятельная работа

4. y = f(x) + b Параллельный перенос вдоль оси ординат

3