853536

1.

Тема урока:Приращение функции

2.

Нахождение значения
функции в точке.
Найти значение функции f(x)= x2 + 2x
в точке x0 = -3.
Решение: f(x0) = f(-3) = (-3)2+ 2∙(-3)
=9-6=3
Ответ: f(-3) = 3

3.

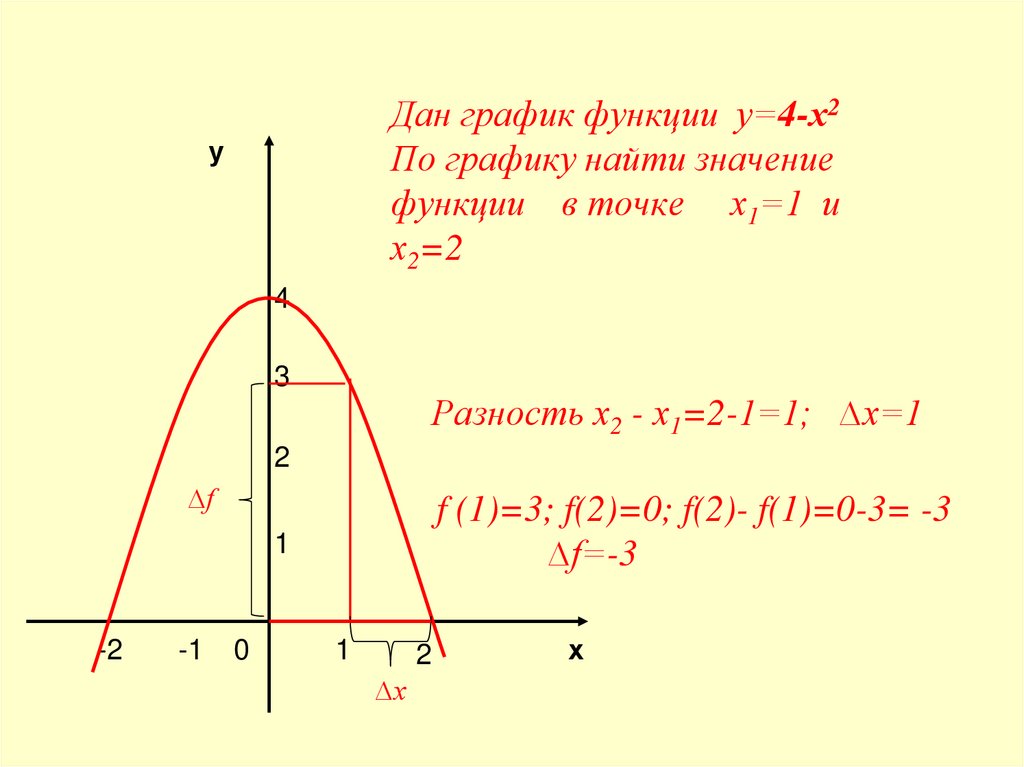
Дан график функции у=4-х2
По графику найти значение
функции в точке х1=1 и
х2=2
у
4
3
Разность х2 - х1=2-1=1; ∆x=1
2
∆f
f (1)=3; f(2)=0; f(2)- f(1)=0-3= -3
∆f=-3
1
-2
-1
0
1
2
∆x
х

4.

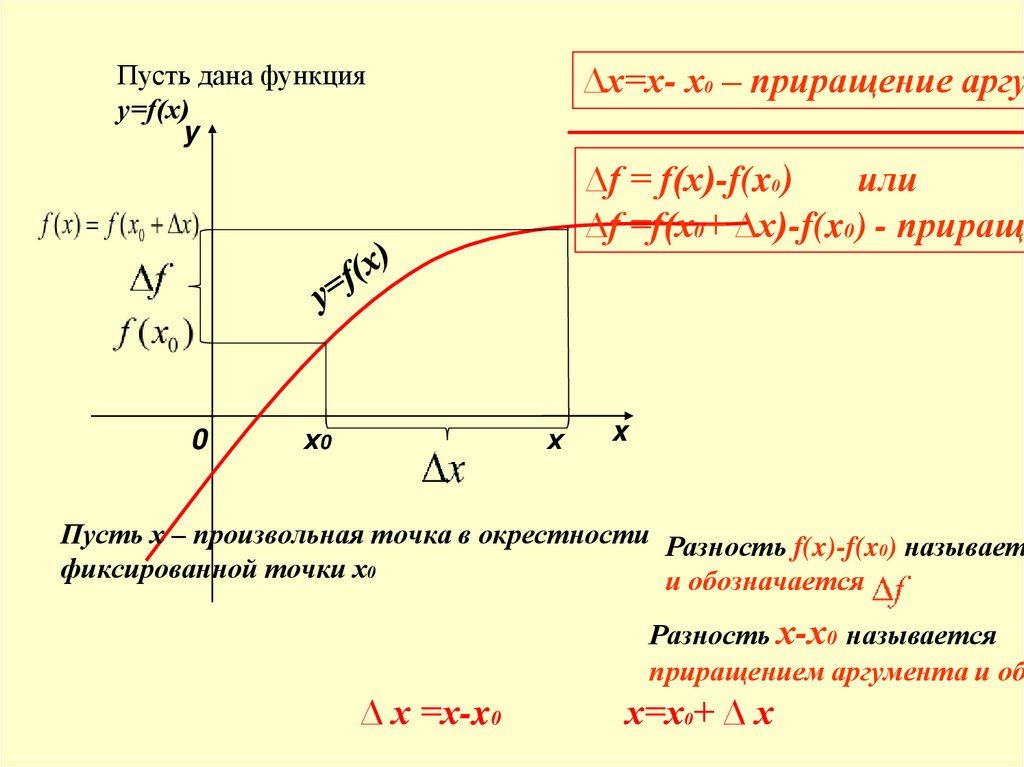
Пусть дана функция
у=f(х)
y
∆х=х- х0 – приращение аргу
∆f = f(x)-f(x0)
или
∆f =f(x0+ ∆x)-f(x0) - прираще
0
х0
х
x
Пусть х – произвольная точка в окрестности Разность f(x)-f(x0) называет
фиксированной точки х0
и обозначается
Разность х-х0 называется
приращением аргумента и об
∆ x =x-x0
х=х0+ ∆ x

5.

• Определение.
Приращением аргумента функции
называется величина, равная разности
между конечным и начальным
значением аргумента: ∆ x =x-x0
• Определение.
Приращением функции называется
величина, равная разности между
конечным и начальным значением
функции ∆f =f(x) - f(x0) = f(х0 + х)– f(x0).

6.

• Δ, δ (название: де́льта, греч. δέλτα) — 4-я
буква греческого алфавита. В системе
греческой алфавитной записи чисел имеет числовое
значение 4. Происходит от Финикийской буквы —
далет, название которой означало «дверь» или «вход в
палатку». От буквы «дельта» произошли латинская
буква D и кириллическая Д. Обозначение приращения
функции (аргумента) буквой дельта впервые применил
швейцарский математик и механик Иоганн Бернулли
(1667-1748)

7.

Пример 1
• Найти приращение аргумента и
приращение функции y=x2 при переходе
от х0=1,2 к точке х=2,5
Решение: ∆ x= х-х0
∆ x=2,5-1,2=1,3,
∆f =f(x) - f(x0)
∆f=2,52-1,22=6,25-1,44= 4,81
Ответ: 1,3; 4,81

8.

Пример 2:
Найти приращение аргумента и приращение
функции в точке х0, если
Решение:

9.

Найдите приращение функции f в точке х0, если
f(x) = 3x+1, x0 = 5, ∆x = 0, 01.
Решение: х=х0+∆x, х= 5+0,01=5,01
f(х0)=f(5)=3·5+1=16;
f (x)=f(5,01)= 3·5,01+1=16,03
Δf = f(x) - f(x0); Δf = 16,03-16=0,03
Ответ: 0,03

10.

Найти приращение функции y=f(x) при переходе от
точки х к точке х+∆x, если f(x)= х2 .
Решение: Δf = f(x) - f(x0)=f(х+ ∆x)-(x)
f(x)=x2
f(х+ ∆x) =(х+ ∆x)2=x2+2x∆x+∆x2
Δf= x2+2x∆x+∆x2 - x2=2x∆x+∆x2
Ответ: 2x∆x+∆x2

11.

Задание
• П.13 изучить, Пример 2 стр 83 выписать
в тетрадь
• № 13.1(в), 13.3 (а)