104___

1. Первообразная и интеграл в заданиях ЕГЭ В 7

Первообразная и интеграл в заданиях ЕГЭ
В7
Учитель:
Митрофанова
О.С.

2. Проверка домашней работы.

3.

Найдем общий вид первообразных функции
По условию искомая первообразная проходит через точку с
координатами (-1; 1,5), значит выполняется равенство
Значит первообразная, которая проходит
через точку А (-1; 1,5), имеет вид

4.

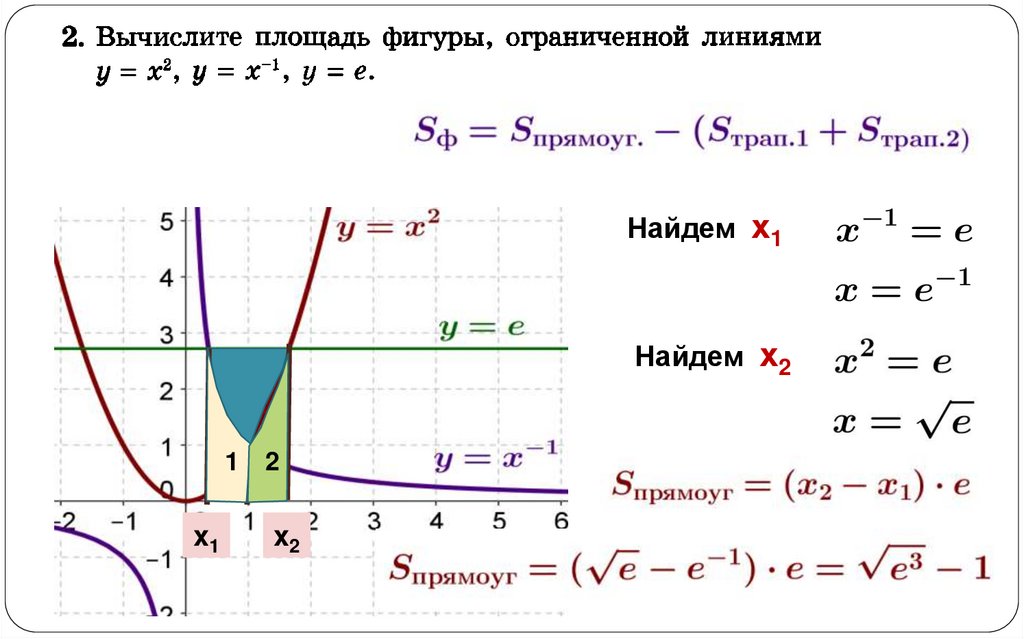
Найдем х1
Найдем х2
1
x1
2
x2

5.

1
1
+2
5

6.

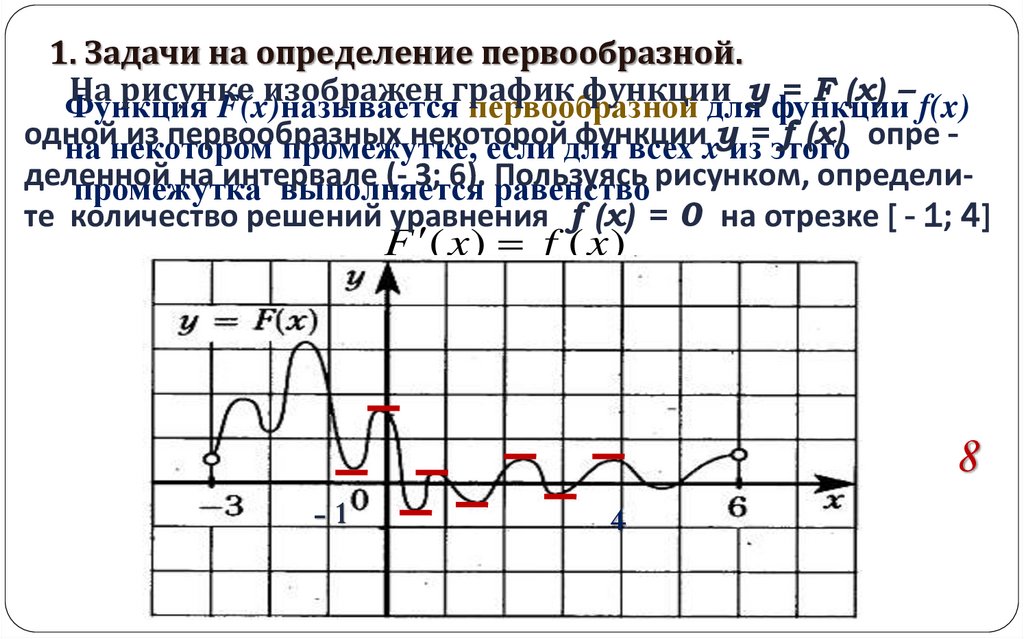
1. Задачи на определение первообразной.
На рисунке
изображен график
функции
= F (x) – f(x)
Функция
F(x)называется
первообразной
дляy функции
одной
из первообразных
некоторой
функции
f (x) опре на некотором
промежутке,
если для
всех xyиз= этого
деленной
на интервале
(- 3; 6). равенство
Пользуясь рисунком, определипромежутка
выполняется
те количество решений уравнения f (x) = 0 на отрезке [ - 1; 4]
F ( x ) f ( x )
8
-1
4

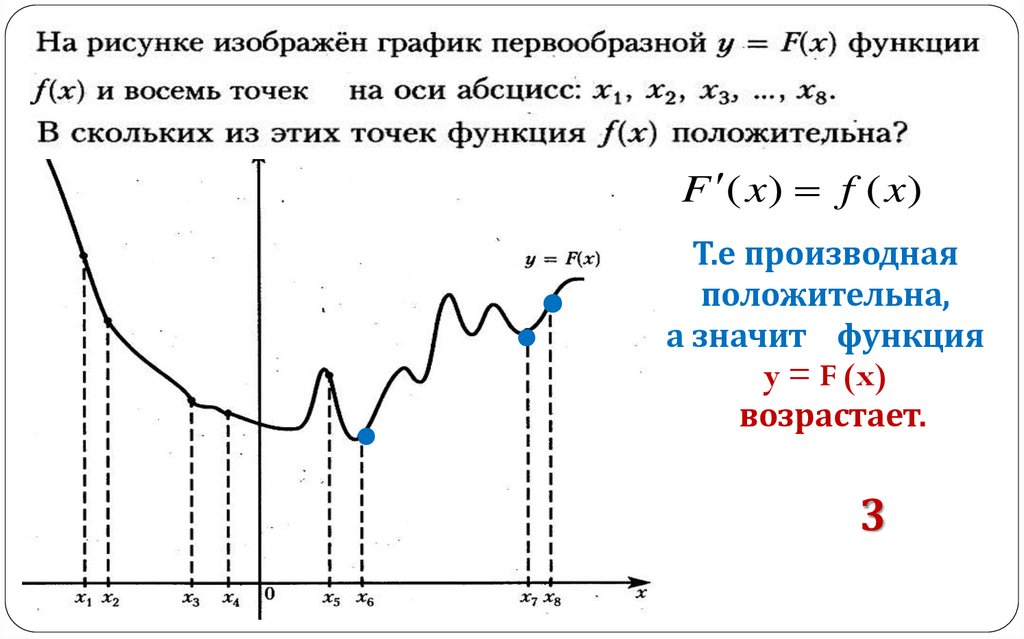
7.

F ( x ) f ( x )
Т.е производная
положительна,
а значит функция
y = F (x)
возрастает.
3

8.

5
По условию F (0) = 5, значит
с=5
= 20 – 8 + 14 – 4 + 5 = 27
27

9.

- 19
10 + с = - 4
с = - 14

10.

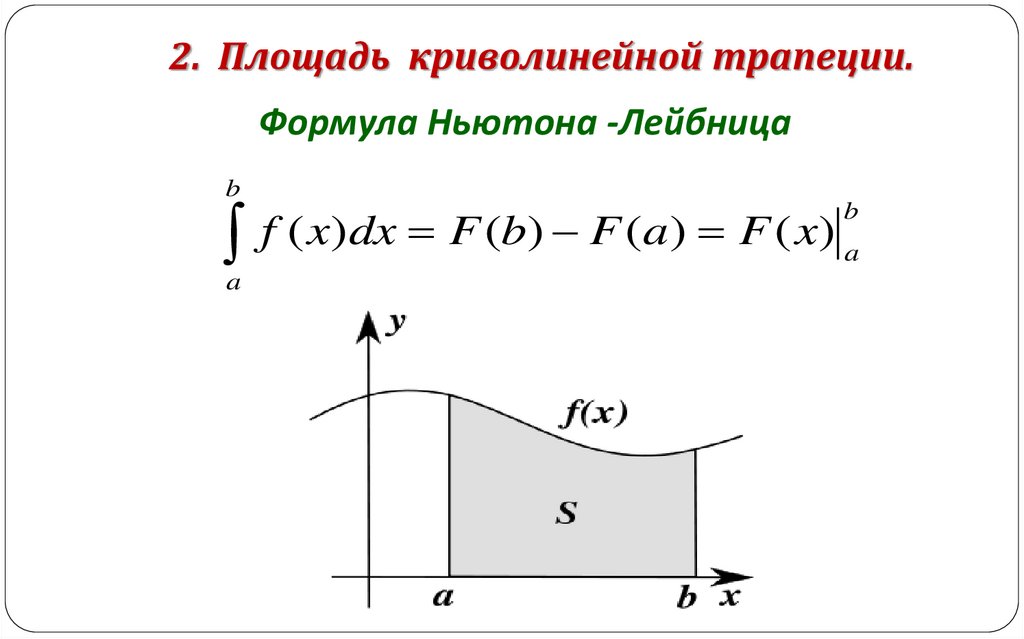
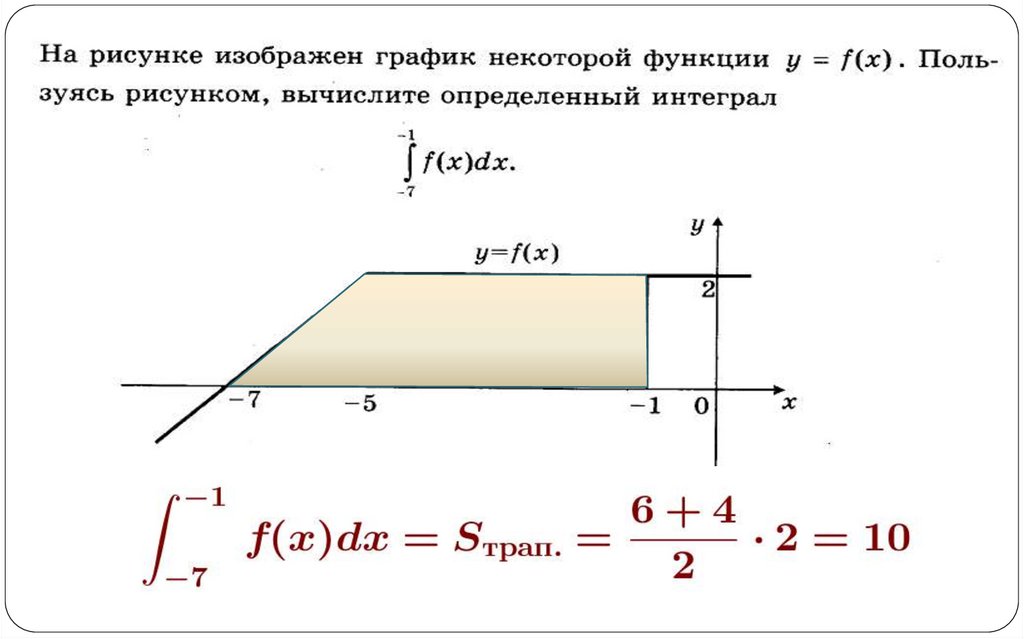
2. Площадь криволинейной трапеции.
Формула Ньютона -Лейбница
b
f ( x)dx F (b) F (a) F ( x)
a
b
a

11.

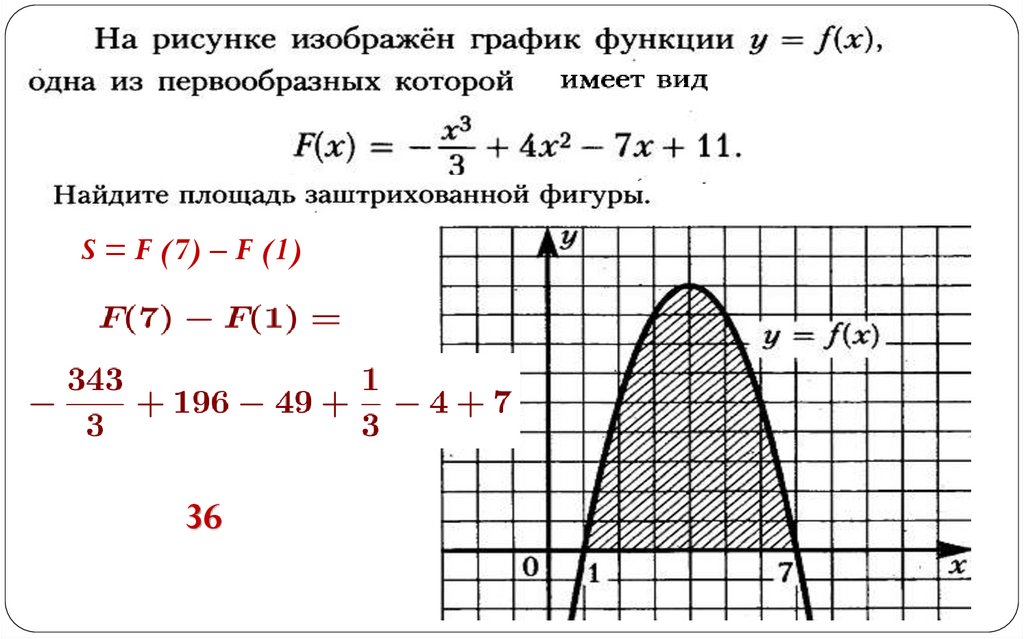
S = F (7) – F (1)
36

12.

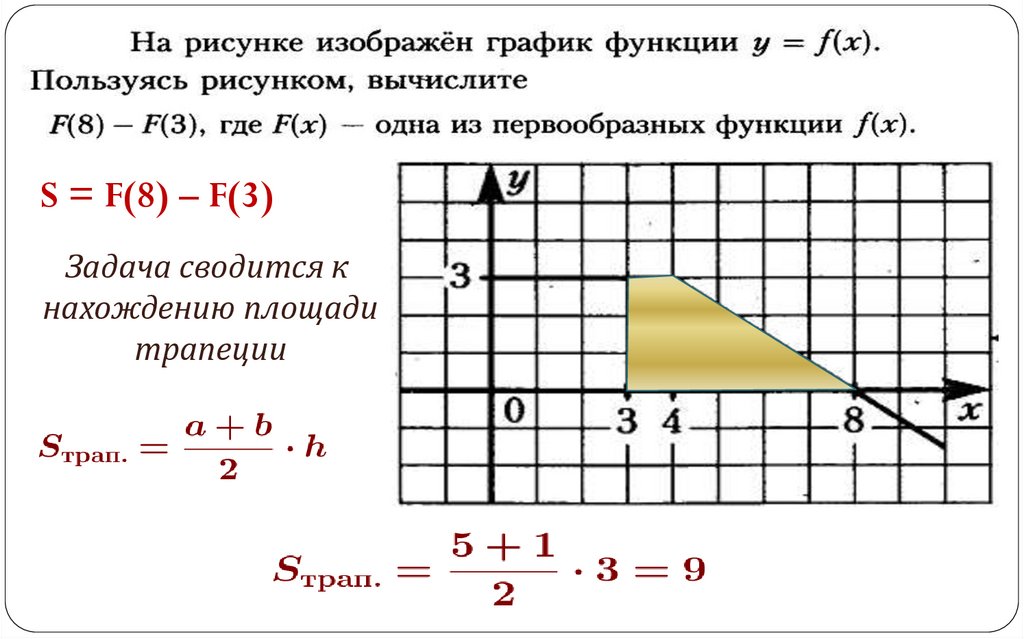
S = F(8) – F(3)
Задача сводится к
нахождению площади
трапеции