Презентация_Кондратьева

1.

АВТОНОМНАЯ НЕКОММЕРЧЕСКАЯ ОРГАНИЗАЦИЯ ВЫСШЕГО ОБРАЗОВАНИЯ
«МОСКОВСКИЙ УНИВЕРСИТЕТ «СИНЕРГИЯ»
Факультет Педагогики и психологии
Направление: Педагогическое образование
Профиль: Педагогика и психология начального образования
ВЫПУСКНАЯ КВАЛИФИКАЦИОННАЯ
– БАКАЛАВРСКАЯ - РАБОТА
на тему:
«РАЗВИТИЕ САМОСТОЯТЕЛЬНОСТИ
У МЛАДШИХ ШКОЛЬНИКОВ НА УРОКАХ
МАТЕМАТИКИ»
Обучающийся: Кондратьева Елена Алексеевна
Руководитель: Москвина Анна Сергеевна

2.

АКТУАЛЬНОСТЬ ТЕМЫ ИССЛЕДОВАНИЯ
Актуальность темы исследования определяется тем, что в начальной школе закладывается способ
отношения ребенка к учению как к собственной деятельности, а не к набору требований взрослого.
Именно в этот период формируются привычки принимать учебную задачу, удерживать цель,
планировать действия и доводить работу до завершения, включая проверку результата.
Математика как учебный предмет делает проблему самостоятельности особенно значимой,
поскольку требует точности, последовательности и контроля каждого шага. Развитие
самостоятельности на уроках математики рассматривается как условие качества
обучения и одновременно как средство поддержки личностного роста: ученик
учится опираться на понятные критерии, видеть собственный прогресс,
исправлять ошибки и принимать ответственность за результат своей работы.
Несмотря на интерес исследователей к особенностям и результатам формирования
самостоятельности младших школьников, проблема развития самостоятельности на уроках
математики остается актуальной. Недостаточная разработанность рекомендаций и методических
разработок по успешному формированию самостоятельности приводит к серьезным проблемам,
связанным с обучением детей.
2

3.

Цель работы: на основе теоретического анализа и полученных эмпирическим путем
данных разработать программу по формированию самостоятельности младших
школьников на уроках математики и экспериментально проверить ее эффективность.
Задачи работы:
раскрыть сущность самостоятельности младших школьников;
проанализировать теоретические подходы к проблеме формирования самостоятельности
младших школьников на уроках математики;
провести эмпирическое исследование уровня самостоятельности младших школьников;
разработать программу развития самостоятельности младших школьников на уроках
математики;
провести анализ результатов формирующего воздействия.
Объект исследования: самостоятельность младших школьников.
Предмет
исследования:
психолого-педагогические
условия
самостоятельности младших школьников на уроках математики.
формирования
3

4.

ГИПОТЕЗА И ЭКСПЕРИМЕНТАЛЬНАЯ БАЗА
ИССЛЕДОВАНИЯ
Гипотезой исследования является предположение о том, что процесс формирования
самостоятельности младших школьников будет проходить успешно, если:
будет своевременно проведена диагностика уровня самостоятельности младших школьников;
будет разработана и реализована Программа, направленную на формирование
самостоятельности младших школьников на уроках математики;
будут учтены возрастные и индивидуальные особенности развития ребенка младшего
школьного возраста.
Экспериментальная база исследования. В исследовании принимали участие
обучающиеся двух 1-х классов МБОУ «Гимназия им. А.Н. Островского», в возрасте от 7 до 8 лет,
общее количество участников 50 человек.
4

5.

МЕТОДЫ ИССЛЕДОВАНИЯ
ТЕОРЕТИЧЕСКИЕ МЕТОДЫ: аналитический; метод синтеза полученных научных
данных; метод тестирования и опроса; математико-аналитический метод.
ЭМПИРИЧЕСКИЕ МЕТОДЫ: Диагностика осуществлялась с помощью следующих
методик:
методика «Диагностика поисковой активности, направленности на конечный результат и
чувства выполненного долга» М.И. Лисиной;
методика «Самооценка силы воли» Н.Н. Обозова;
методика «Карта проявлений самостоятельности» А.М. Щетининой;
методика «Самостоятельность в познавательной деятельности младшего школьника»
А.А. Горичинской.
СТАТИСТИЧЕСКИЕ МЕТОДЫ: с целью подтверждения достоверности полученных
результатов исследования был применен Т-критерий Вилкоксона.
5

6.

Теоретические основы развития самостоятельности
младших школьников на уроках математики
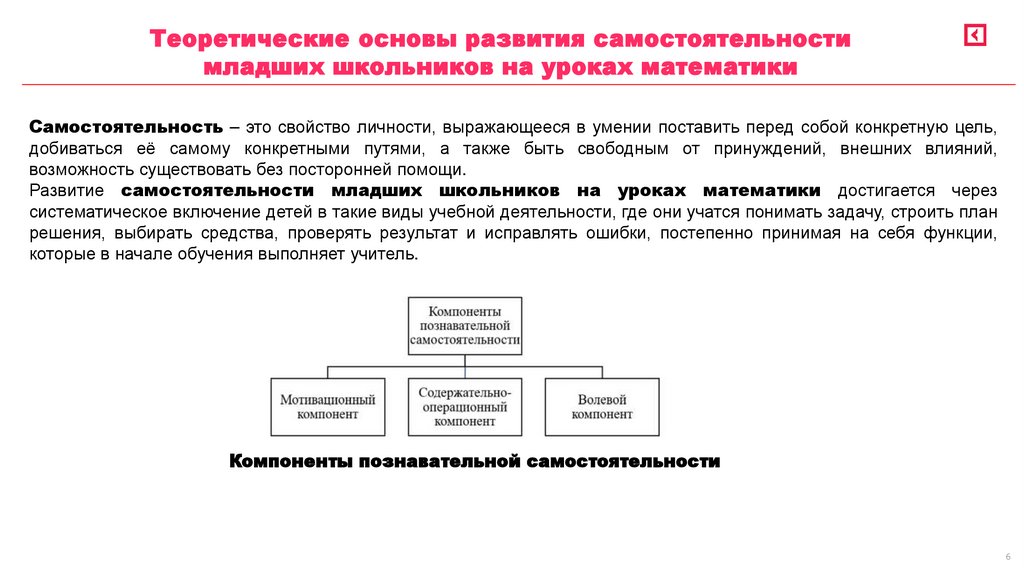
Самостоятельность – это свойство личности, выражающееся в умении поставить перед собой конкретную цель,
добиваться её самому конкретными путями, а также быть свободным от принуждений, внешних влияний,
возможность существовать без посторонней помощи.
Развитие самостоятельности младших школьников на уроках математики достигается через
систематическое включение детей в такие виды учебной деятельности, где они учатся понимать задачу, строить план
решения, выбирать средства, проверять результат и исправлять ошибки, постепенно принимая на себя функции,
которые в начале обучения выполняет учитель.
Компоненты познавательной самостоятельности
6

7.

Результаты исследования уровня развития эмоционально-волевого
компонента младших школьников по методике М.И. Лисиной
в экспериментальной и контрольной группе
(КОНСТАТИРУЮЩИЙ ЭТАП)
Уровень развития эмоционально-волевого
компонента
Высокий
Средний
Низкий
Экспериментальная группа, %
Контрольная группа, %
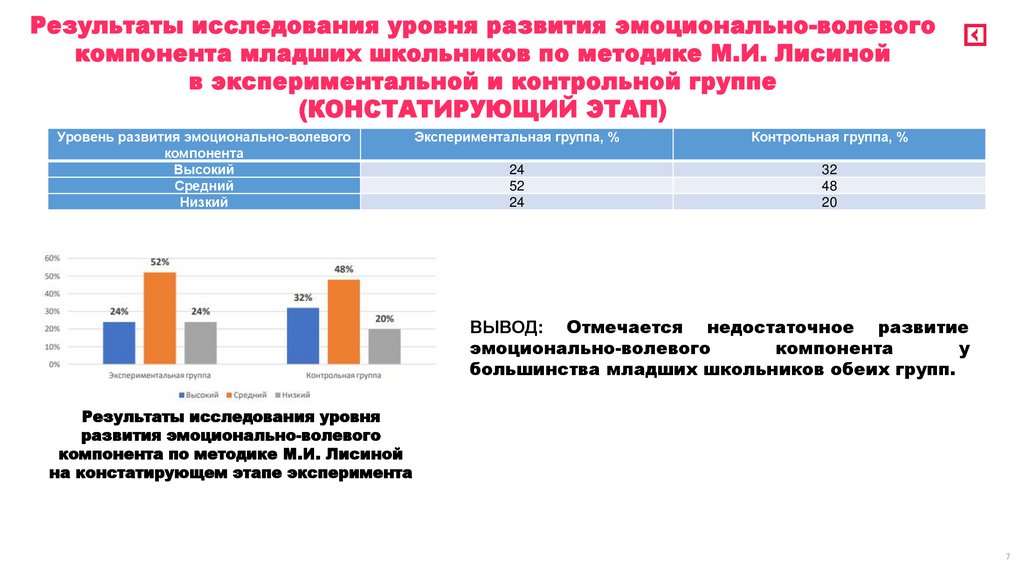
24
52
24
32
48
20
ВЫВОД: Отмечается недостаточное развитие
эмоционально-волевого
компонента
у
большинства младших школьников обеих групп.
Результаты исследования уровня
развития эмоционально-волевого
компонента по методике М.И. Лисиной
на констатирующем этапе эксперимента
7

8.

Результаты исследования по методике Н.Н. Обозова
«Самооценка силы воли» в экспериментальной и контрольной группе
(КОНСТАТИРУЮЩИЙ ЭТАП)
Уровень развития учебной
самостоятельности
Высокий
Средний
Низкий
Экспериментальная группа, %
Контрольная группа, %
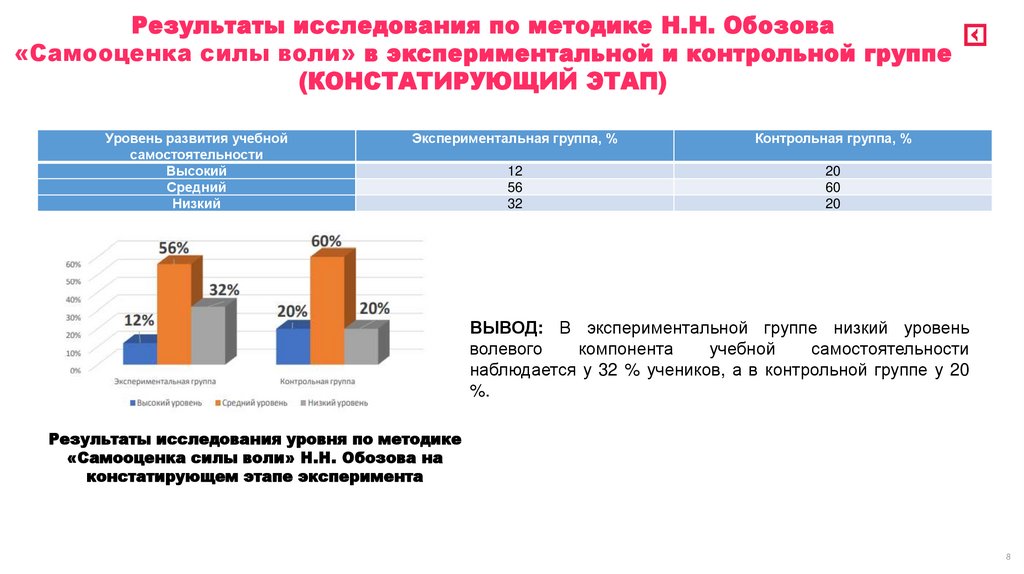
12
56
32
20
60
20
ВЫВОД: В экспериментальной группе низкий уровень
волевого
компонента
учебной
самостоятельности
наблюдается у 32 % учеников, а в контрольной группе у 20
%.
Результаты исследования уровня по методике
«Самооценка силы воли» Н.Н. Обозова на
констатирующем этапе эксперимента
8

9.

Результаты исследования уровня развития учебной
самостоятельности по методике М.А. Щетининой
в экспериментальной и контрольной группе
(КОНСТАТИРУЮЩИЙ ЭТАП)
Уровень развития учебной
самостоятельности
Высокий
Средний
Низкий
Экспериментальная группа, %
Контрольная группа, %
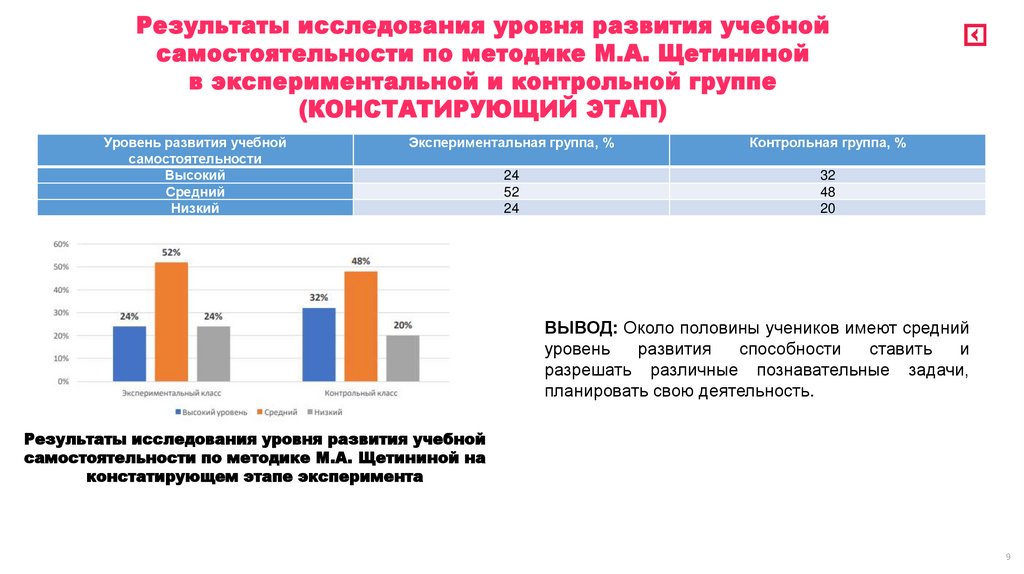
24
52
24
32
48
20
ВЫВОД: Около половины учеников имеют средний
уровень
развития
способности
ставить
и
разрешать различные познавательные задачи,
планировать свою деятельность.
Результаты исследования уровня развития учебной
самостоятельности по методике М.А. Щетининой на
констатирующем этапе эксперимента
9

10.

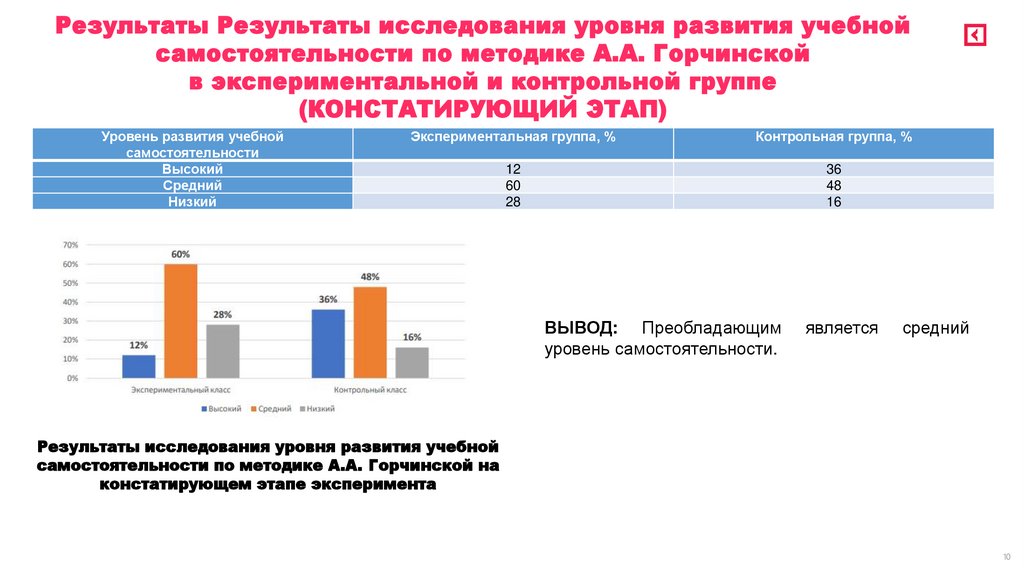
Результаты Результаты исследования уровня развития учебной
самостоятельности по методике А.А. Горчинской
в экспериментальной и контрольной группе
(КОНСТАТИРУЮЩИЙ ЭТАП)
Уровень развития учебной
самостоятельности
Высокий
Средний
Низкий
Экспериментальная группа, %
Контрольная группа, %
12
60
28
36
48
16
ВЫВОД: Преобладающим
уровень самостоятельности.
является
средний
Результаты исследования уровня развития учебной
самостоятельности по методике А.А. Горчинской на
констатирующем этапе эксперимента
10

11.

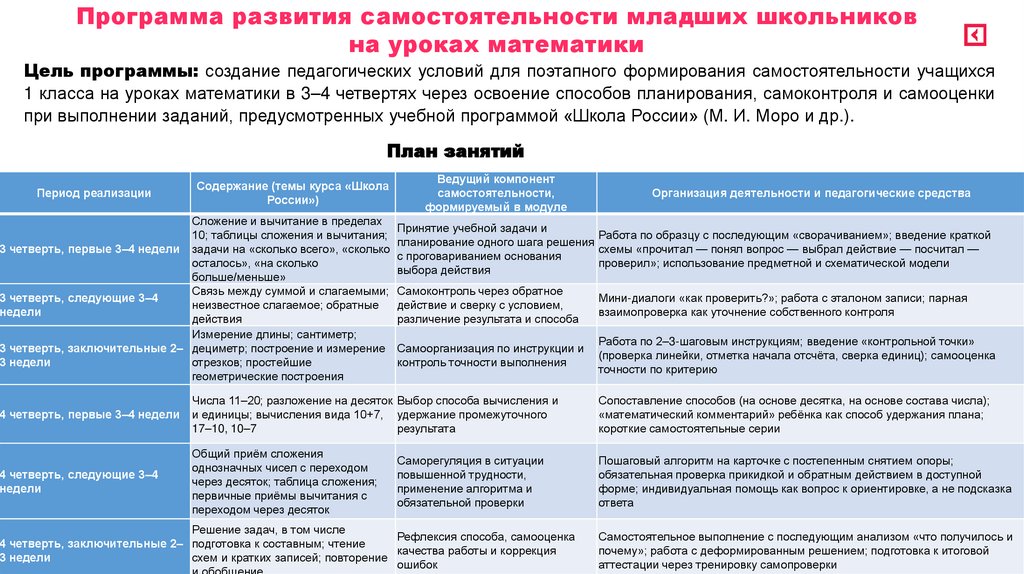
Программа развития самостоятельности младших школьников
на уроках математики
Цель программы: создание педагогических условий для поэтапного формирования самостоятельности учащихся
1 класса на уроках математики в 3–4 четвертях через освоение способов планирования, самоконтроля и самооценки
при выполнении заданий, предусмотренных учебной программой «Школа России» (М. И. Моро и др.).
План занятий
Период реализации
Содержание (темы курса «Школа
России»)
Ведущий компонент
самостоятельности,
формируемый в модуле
Организация деятельности и педагогические средства
Сложение и вычитание в пределах
Принятие учебной задачи и
10; таблицы сложения и вычитания;
Работа по образцу с последующим «сворачиванием»; введение краткой
планирование одного шага решения
3 четверть, первые 3–4 недели задачи на «сколько всего», «сколько
схемы «прочитал — понял вопрос — выбрал действие — посчитал —
с проговариванием основания
осталось», «на сколько
проверил»; использование предметной и схематической модели
выбора действия
больше/меньше»
Связь между суммой и слагаемыми; Самоконтроль через обратное
3 четверть, следующие 3–4
Мини-диалоги «как проверить?»; работа с эталоном записи; парная
неизвестное слагаемое; обратные
действие и сверку с условием,
недели
взаимопроверка как уточнение собственного контроля
действия
различение результата и способа
Измерение длины; сантиметр;
Работа по 2–3-шаговым инструкциям; введение «контрольной точки»
3 четверть, заключительные 2– дециметр; построение и измерение Самоорганизация по инструкции и
(проверка линейки, отметка начала отсчёта, сверка единиц); самооценка
3 недели
отрезков; простейшие
контроль точности выполнения
точности по критерию
геометрические построения
4 четверть, первые 3–4 недели
Числа 11–20; разложение на десяток Выбор способа вычисления и
и единицы; вычисления вида 10+7, удержание промежуточного
17–10, 10–7
результата
Сопоставление способов (на основе десятка, на основе состава числа);
«математический комментарий» ребёнка как способ удержания плана;
короткие самостоятельные серии
4 четверть, следующие 3–4
недели
Общий приём сложения
однозначных чисел с переходом
через десяток; таблица сложения;
первичные приёмы вычитания с
переходом через десяток
Пошаговый алгоритм на карточке с постепенным снятием опоры;
обязательная проверка прикидкой и обратным действием в доступной
форме; индивидуальная помощь как вопрос к ориентировке, а не подсказка
ответа
Саморегуляция в ситуации
повышенной трудности,
применение алгоритма и
обязательной проверки
Решение задач, в том числе
Рефлексия способа, самооценка
4 четверть, заключительные 2– подготовка к составным; чтение
качества работы и коррекция
3 недели
схем и кратких записей; повторение
ошибок
и обобщение
Самостоятельное выполнение с последующим анализом «что получилось и
почему»; работа с деформированным решением; подготовка к итоговой 11
аттестации через тренировку самопроверки

12.

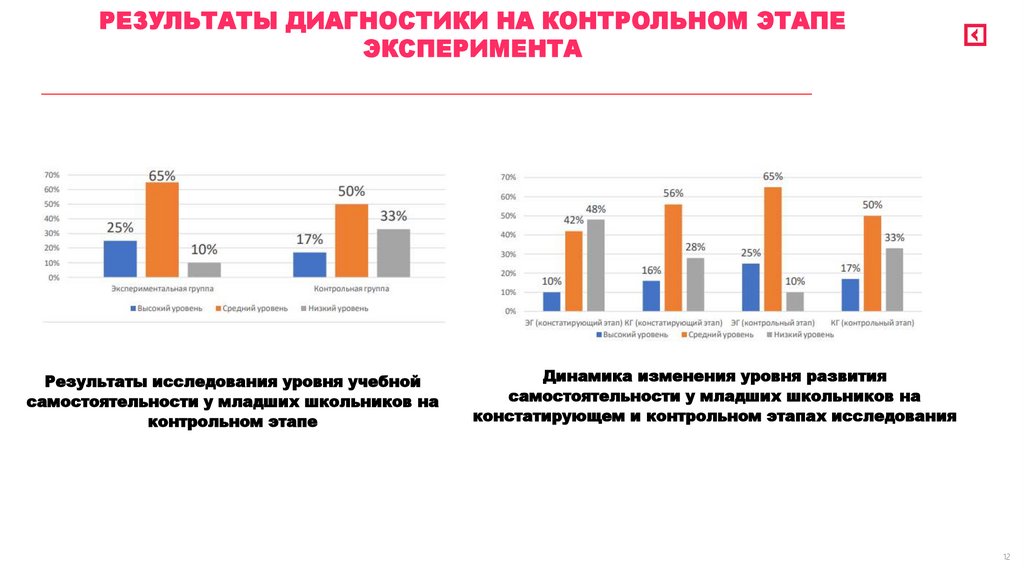
РЕЗУЛЬТАТЫ ДИАГНОСТИКИ НА КОНТРОЛЬНОМ ЭТАПЕ
ЭКСПЕРИМЕНТА
Результаты исследования уровня учебной
самостоятельности у младших школьников на
контрольном этапе
Динамика изменения уровня развития
самостоятельности у младших школьников на
констатирующем и контрольном этапах исследования
12

13.

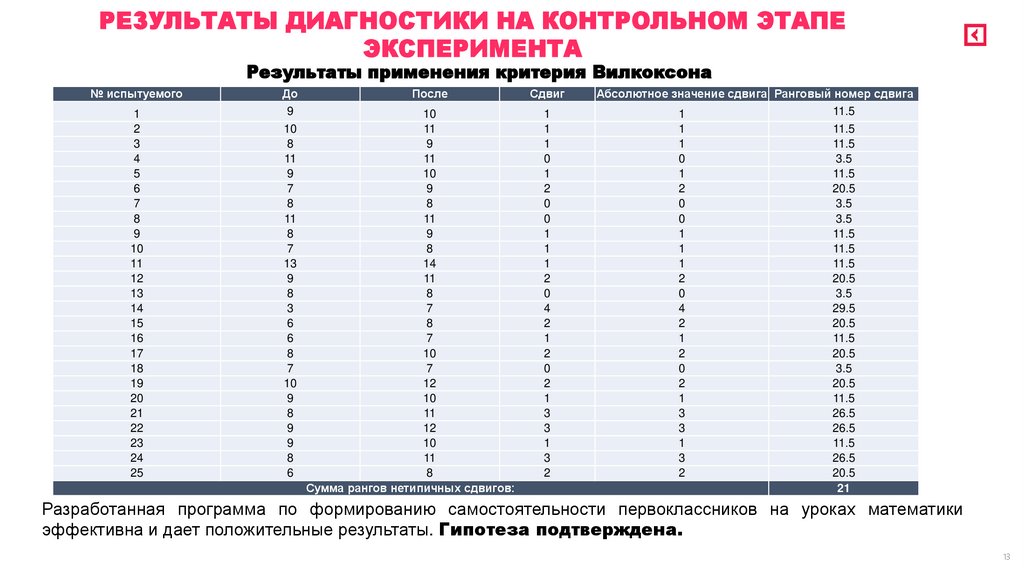
РЕЗУЛЬТАТЫ ДИАГНОСТИКИ НА КОНТРОЛЬНОМ ЭТАПЕ
ЭКСПЕРИМЕНТА
Результаты применения критерия Вилкоксона
№ испытуемого
До
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
9
10
8
11
9
7
8
11
8
7
13
9
8
3
6
6
8
7
10
9
8
9
9
8
6
После
10
11
9
11
10
9
8
11
9
8
14
11
8
7
8
7
10
7
12
10
11
12
10
11
8
Сумма рангов нетипичных сдвигов:
Сдвиг
1
1
1
0
1
2
0
0
1
1
1
2
0
4
2
1
2
0
2
1
3
3
1
3
2
Абсолютное значение сдвига Ранговый номер сдвига
1
1
1
0
1
2
0
0
1
1
1
2
0
4
2
1
2
0
2
1
3
3
1
3
2
11.5
11.5
11.5
3.5
11.5
20.5
3.5
3.5
11.5
11.5
11.5
20.5
3.5
29.5
20.5
11.5
20.5
3.5
20.5
11.5
26.5
26.5
11.5
26.5
20.5
21
Разработанная программа по формированию самостоятельности первоклассников на уроках математики
эффективна и дает положительные результаты. Гипотеза подтверждена.
13

14.

СПАСИБО ЗА
ВНИМАНИЕ!