569140a29b3a4cf19a11de48b0819aeb

1. Объем прямой призмы и цилидра

Урок геометрии в 11 классе.

2. СВЕДЕНИЯ ИЗ ПЛАНИМЕТРИИ

3.

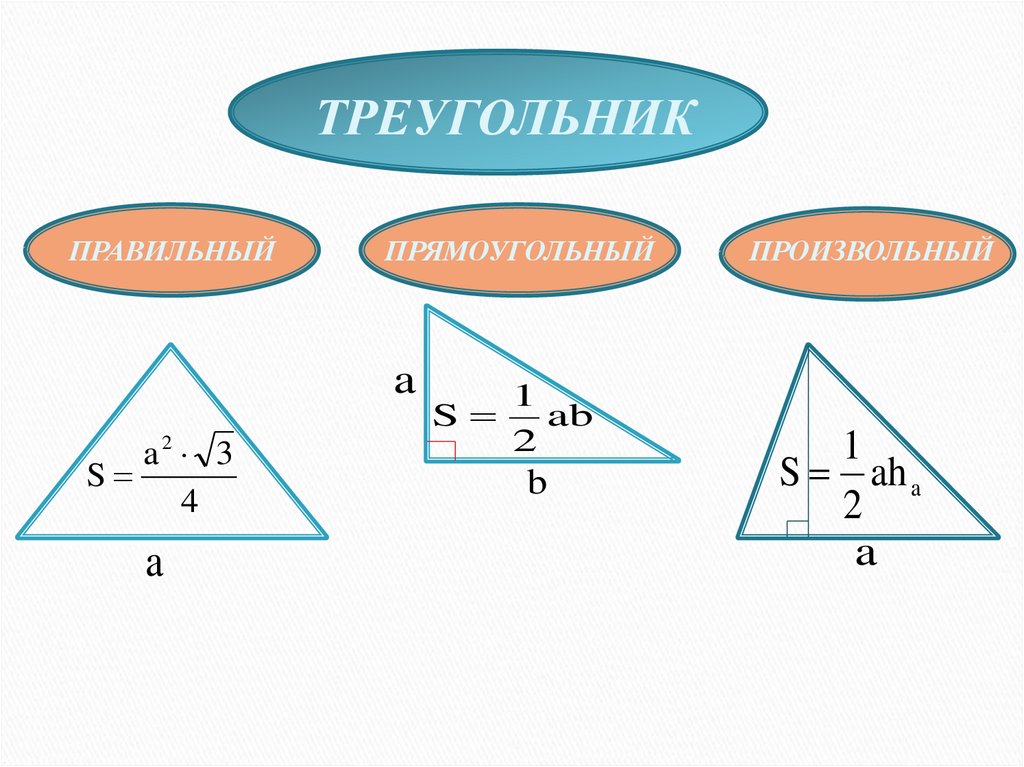
ТРЕУГОЛЬНИК
ПРАВИЛЬНЫЙ
ПРЯМОУГОЛЬНЫЙ
a
a2 3
S
4
a
S
1
ab
2
b
ПРОИЗВОЛЬНЫЙ
1
S ah a
2
a

4.

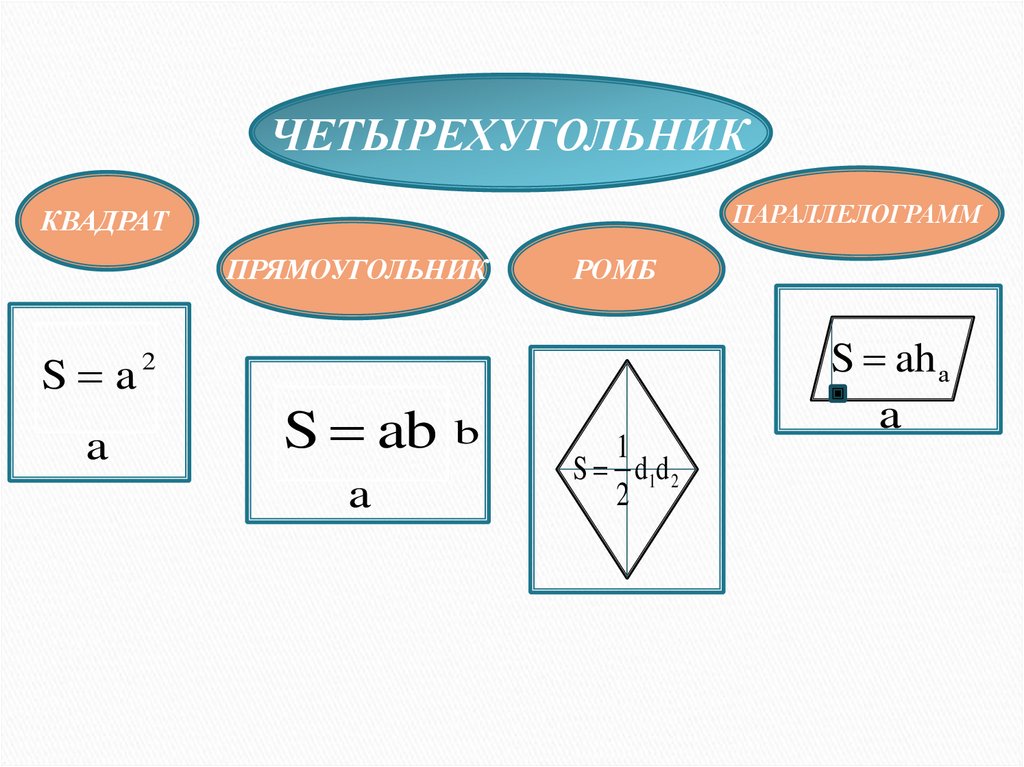
ЧЕТЫРЕХУГОЛЬНИК
ПАРАЛЛЕЛОГРАММ
КВАДРАТ
ПРЯМОУГОЛЬНИК
S a
a
РОМБ
2
S ab b
a
1
S d1d 2
2
S ah а
a

5.

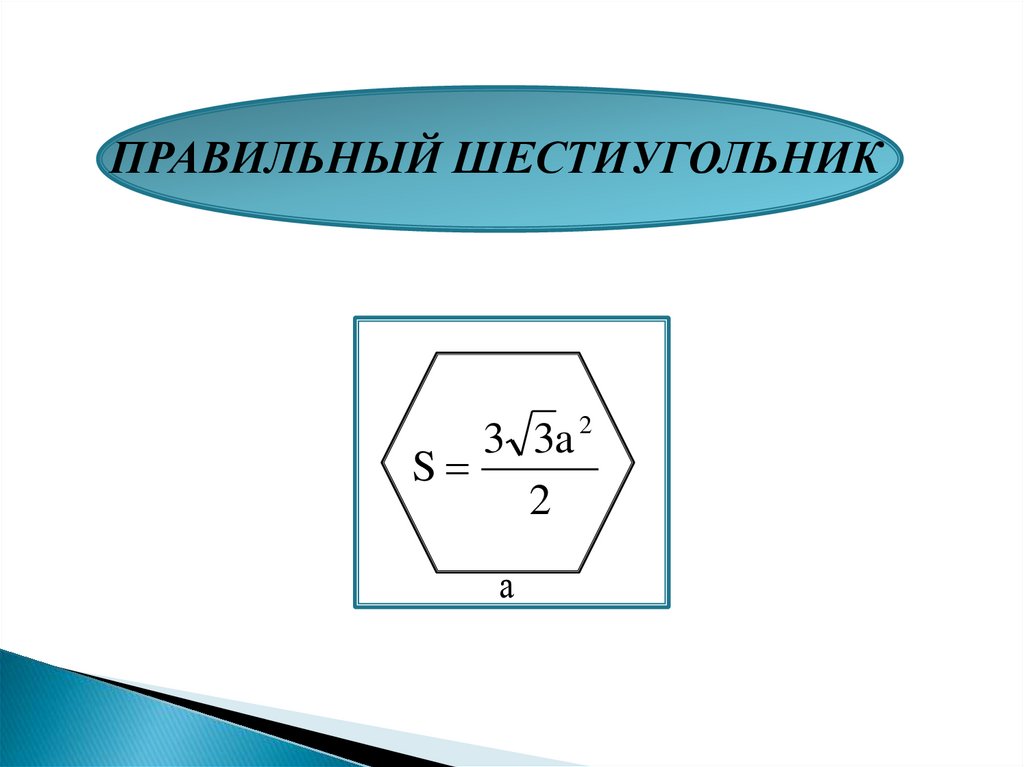
ПРАВИЛЬНЫЙ ШЕСТИУГОЛЬНИК
3 3a 2
S
2
а

6.

ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯ
РАДИУСА ВПИСАННОЙ И ОПИСАННОЙ
ОКРУЖНОСТИ
Правильный треугольник
r
a
3
6
, R
a
3
3
a b c
1
,
R
с, где с гипотенуза
Прямоугольный треугольник
2
2
a
r
, R a 2
Квадрат
2
2
1
R
d, где d диагональ
Прямоугольник
2
r
Правильный шестиугольник
r
a 3
,
2
R а

7. Некоторые отношения подобия

Отношение периметров подобных
многоугольников равно коэффициенту
подобия.
Отношение площадей подобных фигур
равно квадрату коэффициента подобия.
Отношение объемов подобных тел равно
кубу коэффициента подобия.

8. ОБЪЕМ ПРИЗМЫ

9.

Теорема
Объём прямой призмы равен
произведению площади
основания на высоту
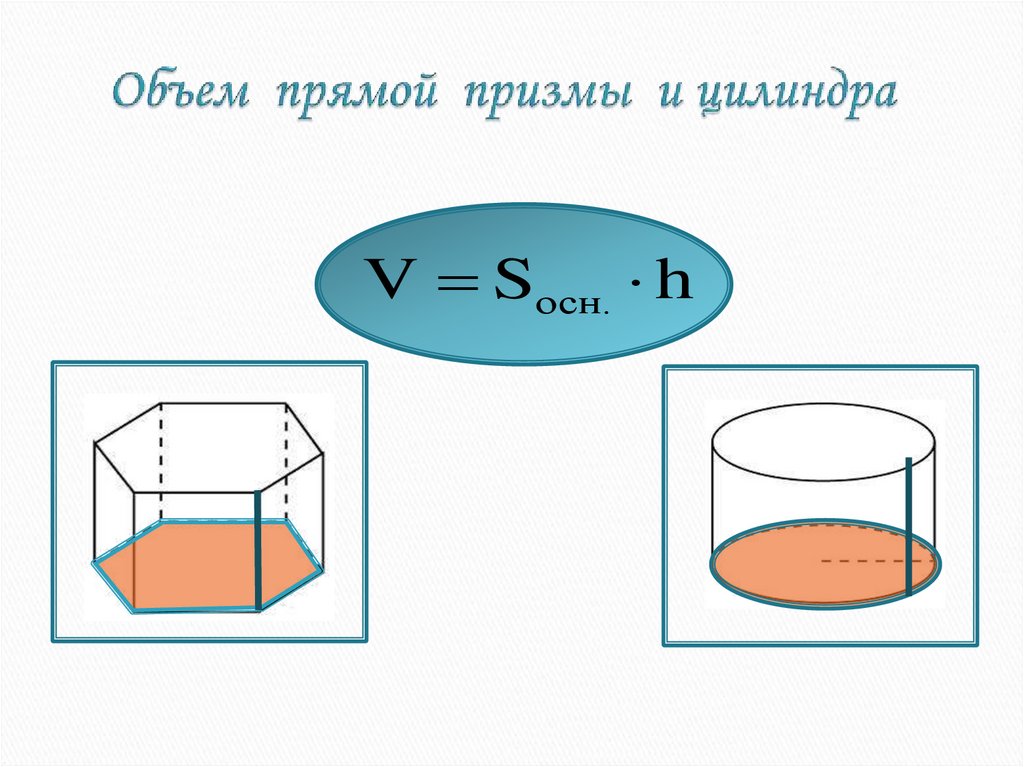
V = Sосн. · h

10.

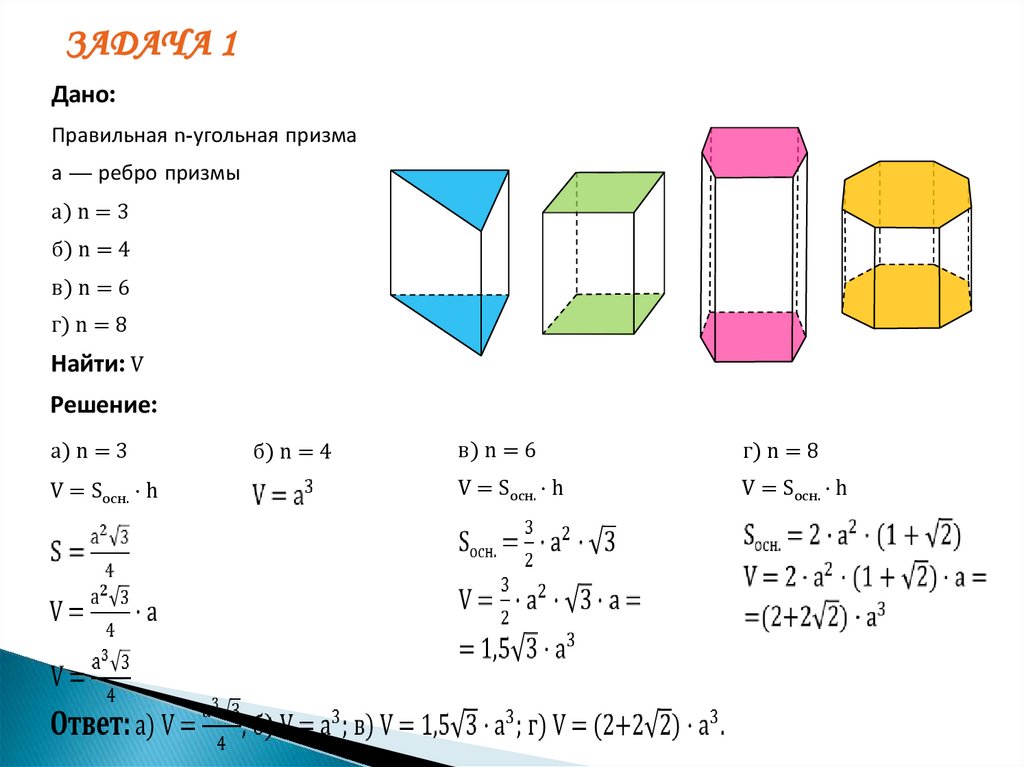
ЗАДАЧА 1
Дано:
Правильная n-угольная призма
а — ребро призмы
а) n = 3
б) n = 4
в) n = 6
г) n = 8
Найти: V
Решение:
a) n = 3
V = Sосн. · h
б) n = 4
в) n = 6
г) n = 8
V = Sосн. · h
V = Sосн. · h

11. ЗАДАЧА 2

Основанием
прямой
треугольной
призмы
служит
прямоугольный треугольник с катетами 6 и 8, боковое ребро
равно 5. Найдите объем призмы.
h
a
b
Ответ : 120

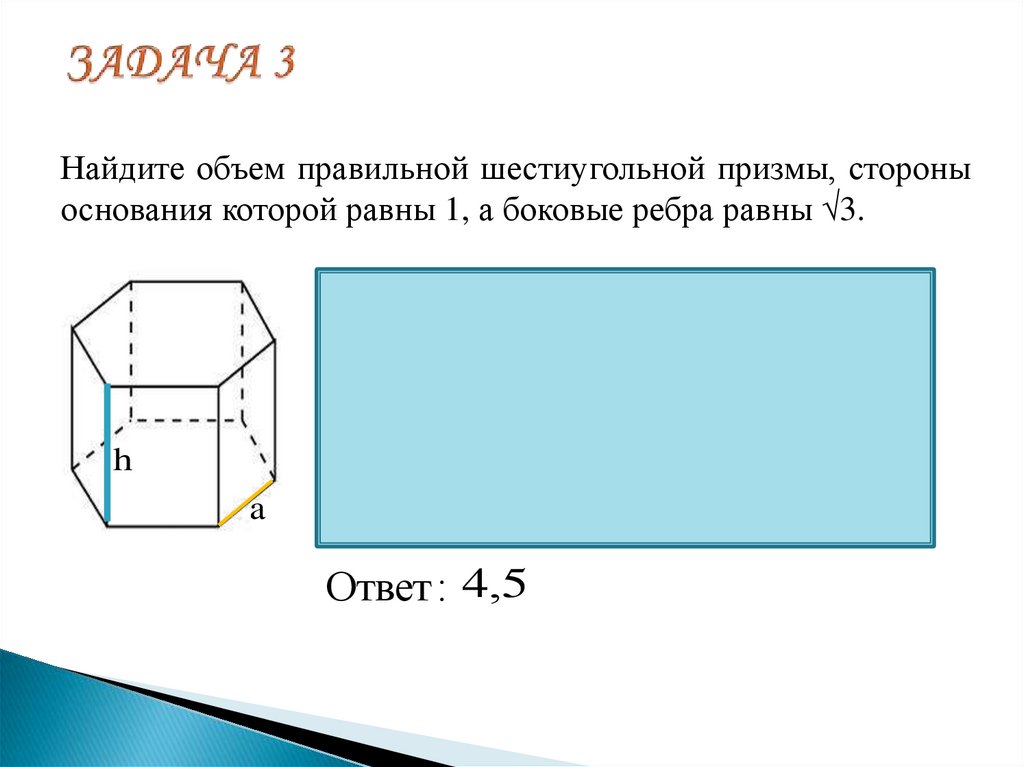
12. ЗАДАЧА 3

Найдите объем правильной шестиугольной призмы, стороны
основания которой равны 1, а боковые ребра равны √3.
h
a
Ответ : 4,5

13. ЗАДАЧА 4

В сосуд, имеющий форму правильной треугольной призмы,
налили воду. Уровень воды достигает 80 см. На какой высоте
будет находиться уровень воды, если ее перелить в другой
такой же сосуд, у которого сторона основания в 4 раза
больше, чем у первого? Ответ выразите в см.
h1
h2
Ответ : 5

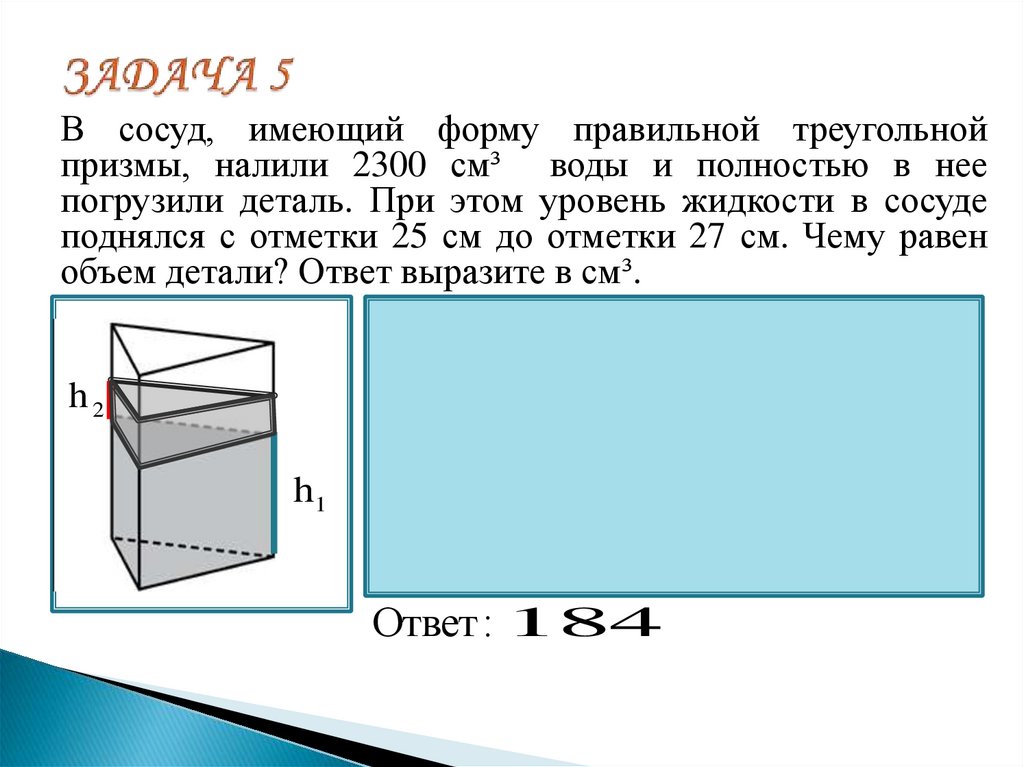
14. ЗАДАЧА 5

В сосуд, имеющий форму правильной треугольной
призмы, налили 2300 см³ воды и полностью в нее
погрузили деталь. При этом уровень жидкости в сосуде
поднялся с отметки 25 см до отметки 27 см. Чему равен
объем детали? Ответ выразите в см³.
h2
h1
Ответ : 184

15. ОБЪЕМ цилиндра

16.

Теорема
Объём цилиндра равен произведению
площади основания на высоту
2
V = πr h

17. Объем прямой призмы и цилиндра

V Sосн. h

18.

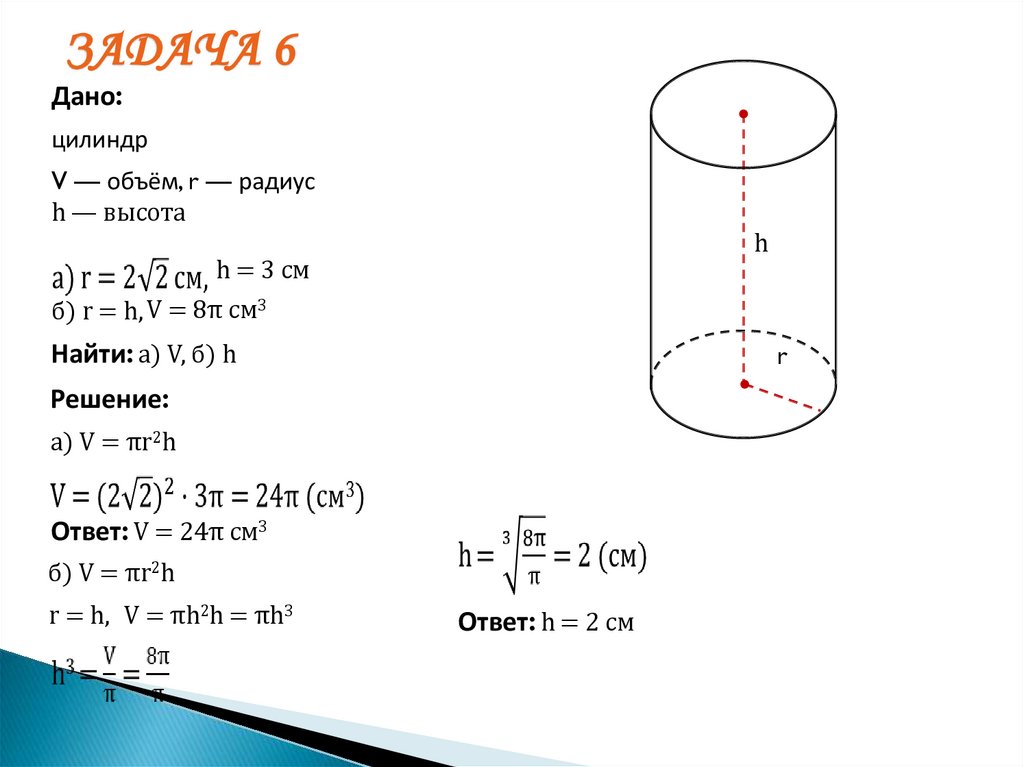
ЗАДАЧА 6
Дано:
цилиндр
V — объём, r — радиус
h — высота
h
h = 3 см
б) r = h, V = 8π см3
r
Найти: а) V, б) h
Решение:
a) V = πr2h
Ответ: V = 24π см3
б) V = πr2h
r = h, V = πh2h = πh3
Ответ: h = 2 см

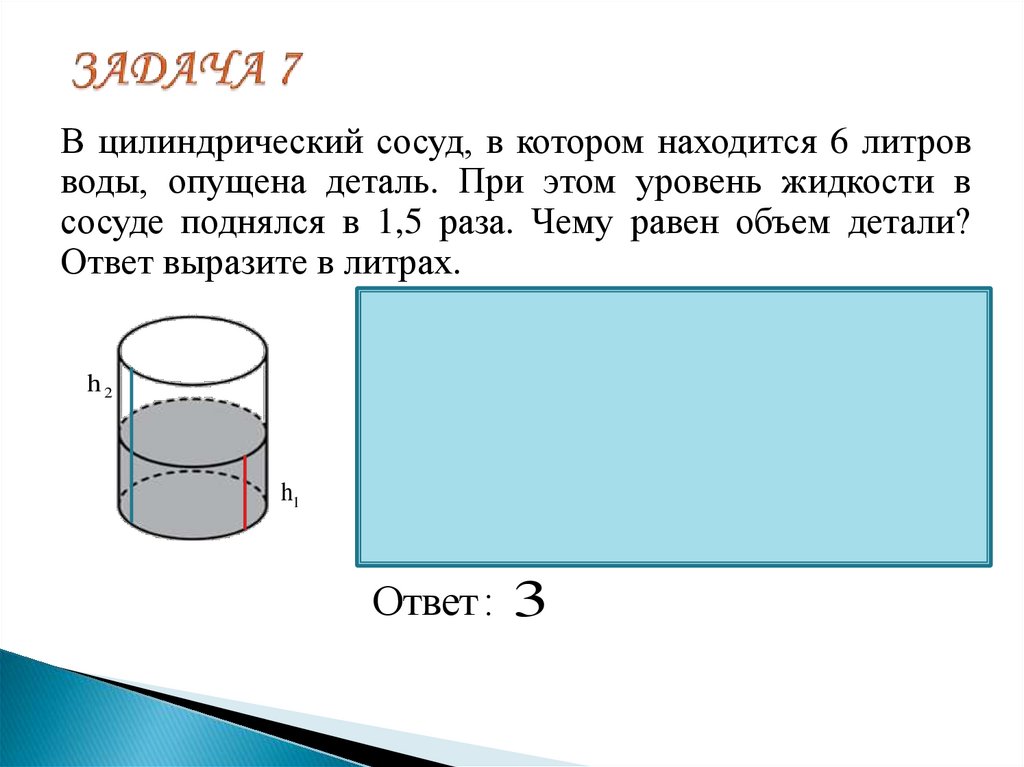
19. ЗАДАЧА 7

В цилиндрический сосуд, в котором находится 6 литров
воды, опущена деталь. При этом уровень жидкости в
сосуде поднялся в 1,5 раза. Чему равен объем детали?
Ответ выразите в литрах.
h2
h1
Ответ : 3

20. ЗАДАЧА 8

Объем первого цилиндра равен 12 м3. У второго цилиндра
высота в три раза больше, а радиус основания — в два раза
меньше, чем у первого. Найдите объем второго цилиндра.
Ответ дайте в кубических метрах.
Ответ : 9

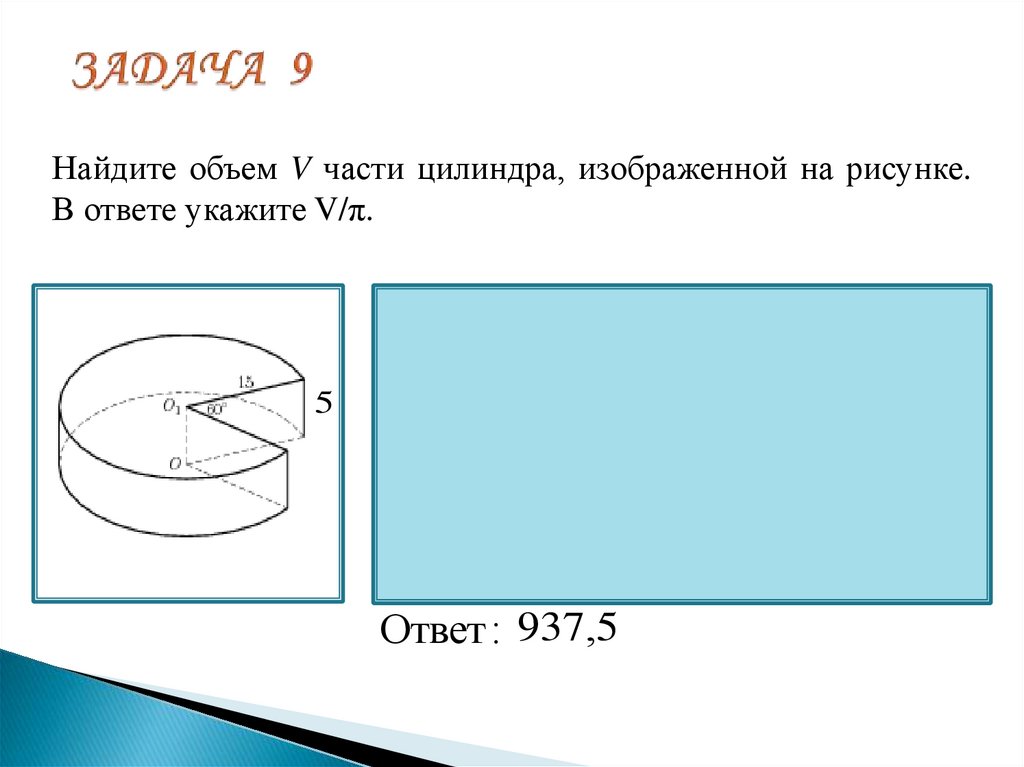
21. ЗАДАЧА 9

Найдите объем V части цилиндра, изображенной на рисунке.
В ответе укажите V/π.
5
Ответ : 937,5

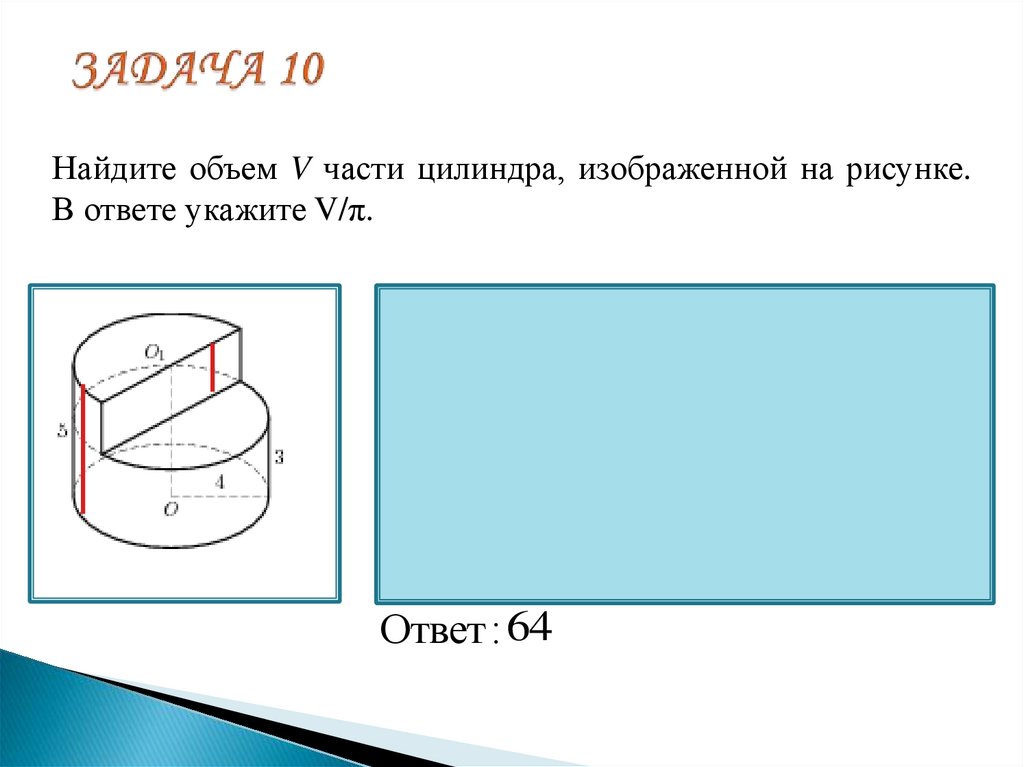
22. ЗАДАЧА 10

Найдите объем V части цилиндра, изображенной на рисунке.
В ответе укажите V/π.
Ответ : 64

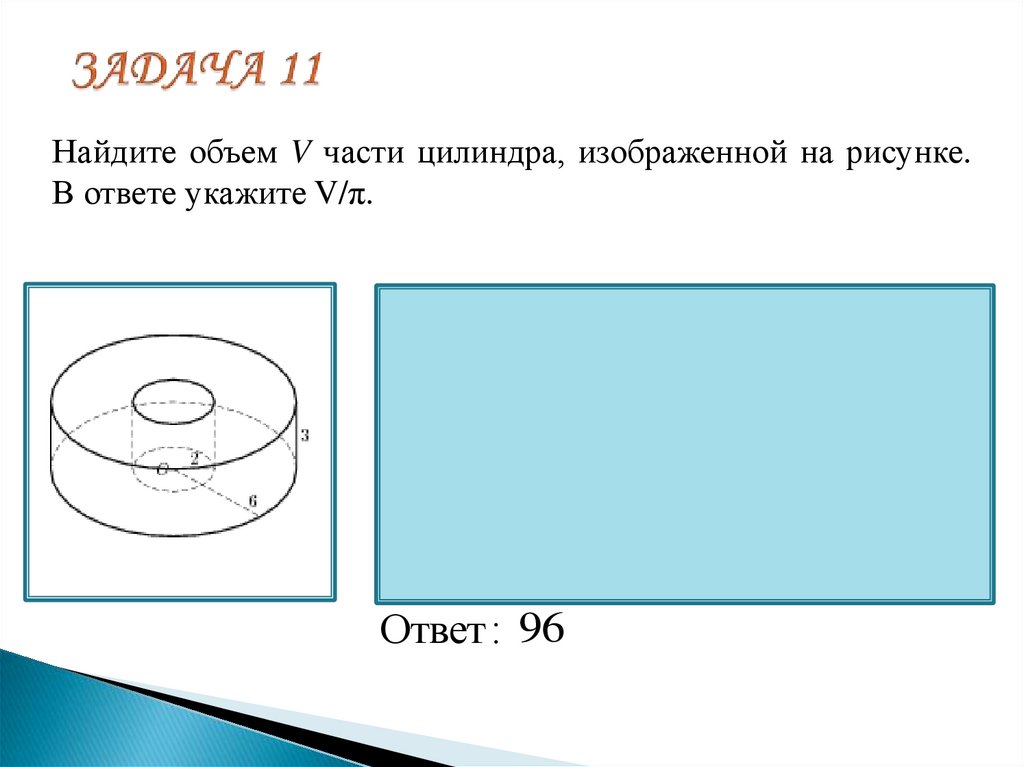
23. ЗАДАЧА 11

Найдите объем V части цилиндра, изображенной на рисунке.
В ответе укажите V/π.
Ответ : 96