Similar presentations:
ТМОИС 01_2
1. Тема 1. Цели и задачи курса. Введение в теорию множеств
"ТЕОРЕТИКО-МНОЖЕСТВЕННЫЕОСНОВЫ ИНТЕЛЛЕКТУАЛЬНЫХ СИСТЕМ“
Лекция 1 (ч.2)
2. Высказывательный способ
Высказывательный способ состоит в заданиитакого свойства, наличие которого у элементов
определенного множества является истиной (а для
остальных элементов U – ложью).
Пусть P(x) — утверждение, заключающееся в том,
что элемент х обладает свойством Р. Тогда запись
X = {x∈M | P(x)}
означает, что множество Х состоит из элементов
некоторого множества М со свойством Р.
3. Перечислительный способ
Перечислительный способ состоит всоставлении полного списка элементов
множества, заключенного в фигурные скобки.
Применяется, в основном, для конечных
множеств с небольшим числом элементов.
Множество записывается в следующей
форме:
X = {x1,x2, … ,xn}.
4. «Наивная» теория множеств
Теория множеств без ограниченийна способы задания множеств называется
наивной теорией множеств.
Проблема: наличие парадоксов
Почему? Наш естественный язык, наши мысли и
идеи – вообще человеческое мышление как
таковое – не особо подходит для выражения
фундаментальных принципов мироздания
5. Парадокс Рассела
Существуют множества, содержащие себя как свойсобственный элемент. Значит, существуют и
множества, которые сами себя не содержат.
Пусть Y – класс всех таких множеств, т.е. множество
всех множеств, не содержащих себя как элемент.
Тогда есть ровно две возможности:
• Допустим, Y∈ Y. Тогда Y∉ Y по определению,
противоречие.
• Значит, Y∉ Y . Но тогда Y∈ Y тоже по
определению. Снова противоречие. ЧТО???
6. Решение
Избежать парадоксов (до определенногопредела) удается в рамках
аксиоматической теории множеств.
На текущий момент
теория множеств Цермело-Френкеля (ZF)
является общепризнанной и широко
используемой на практике, пусть у нее есть и
свои собственные проблемы.
7. Начала геометрии
Самая первая аксиоматическая система –«Начала» Евклида, III век до н.э.
Проблема: постулат (аксиома) №5
«Через точку на плоскости можно провести
только одну прямую, параллельную данной»
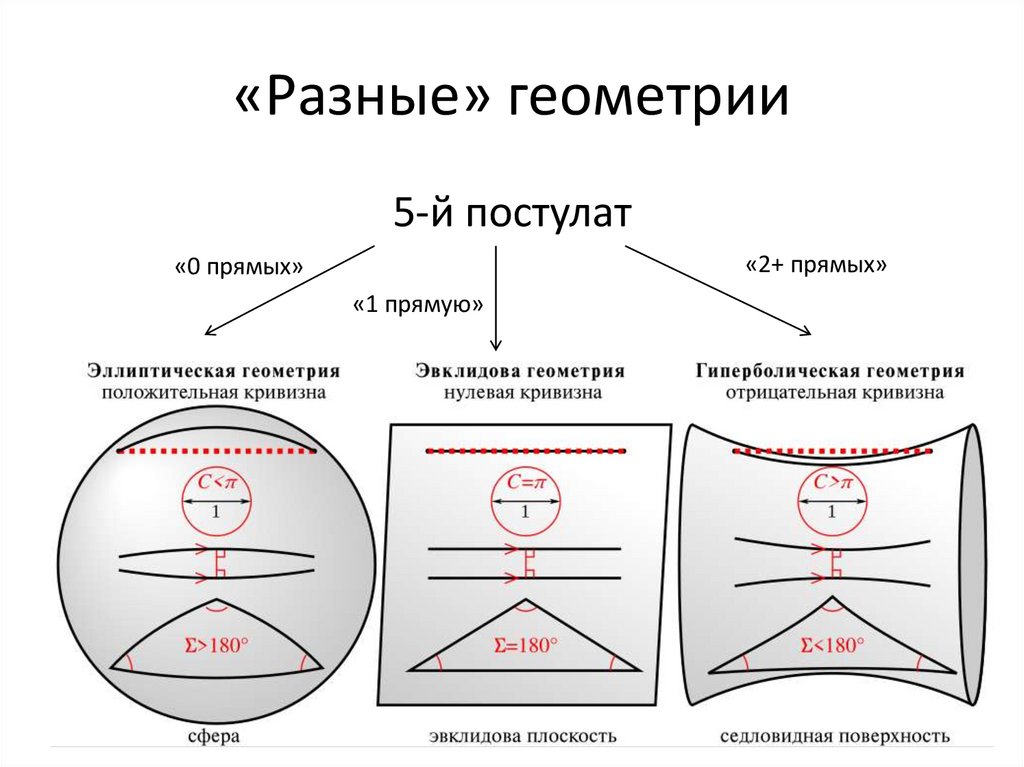
8. «Разные» геометрии
5-й постулат«2+ прямых»
«0 прямых»
«1 прямую»
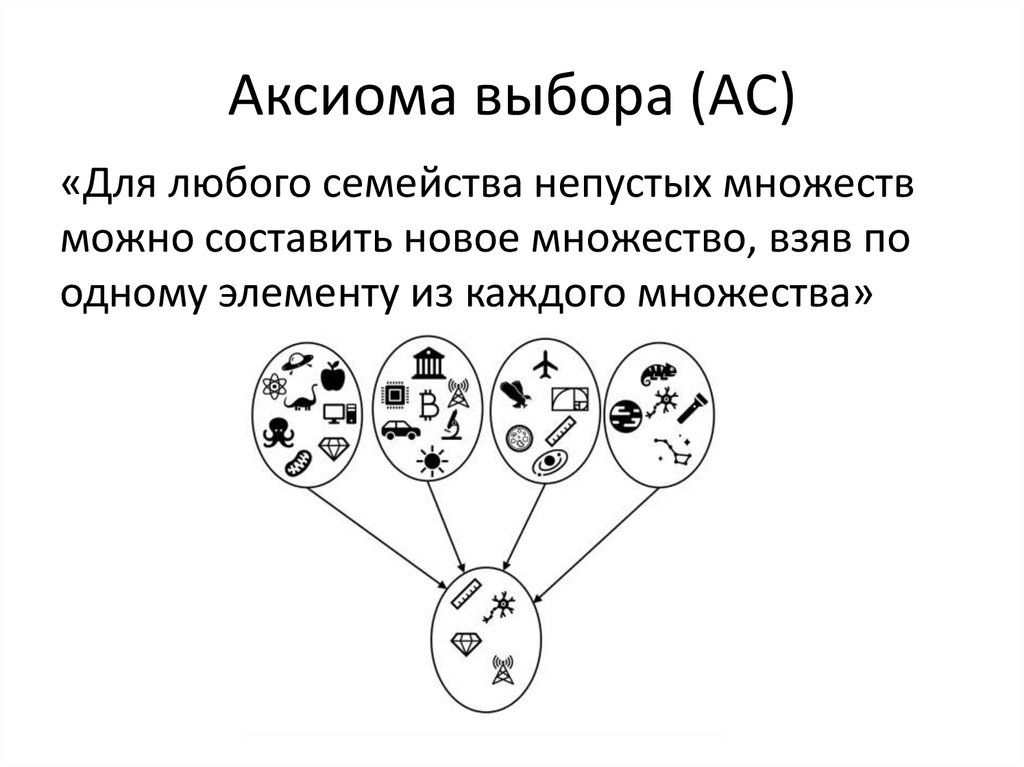
9. Аксиома выбора (AC)
«Для любого семейства непустых множествможно составить новое множество, взяв по
одному элементу из каждого множества»
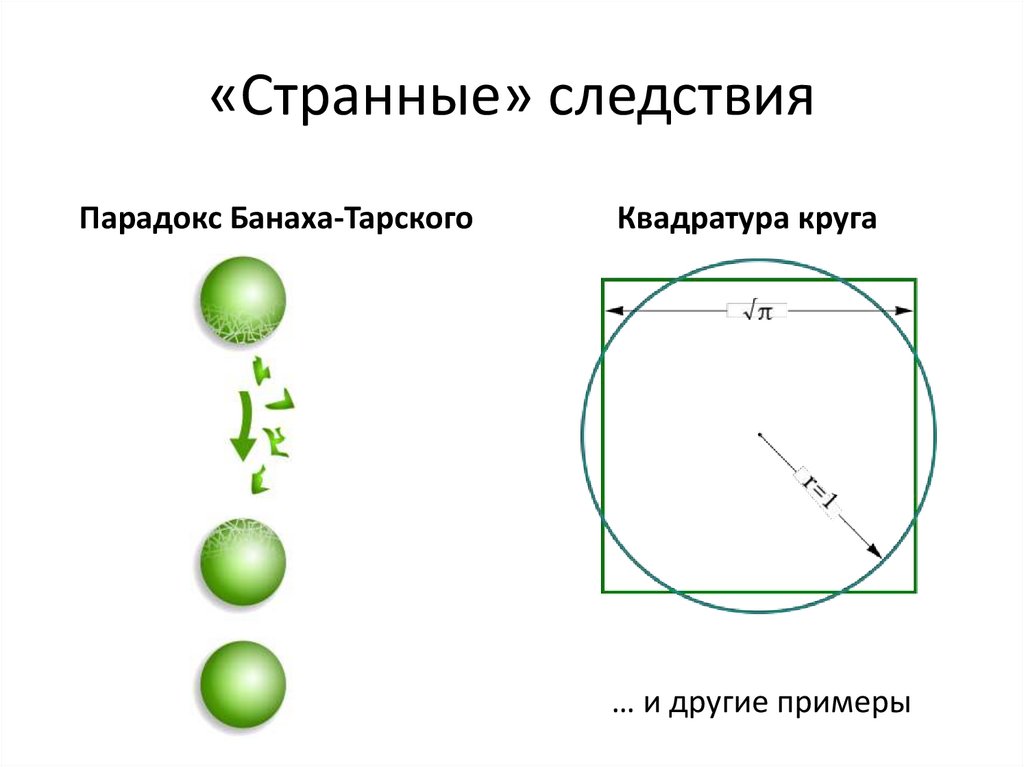
10. «Странные» следствия
Парадокс Банаха-ТарскогоКвадратура круга
… и другие примеры
11. Теорема Гёделя о неполноте
На самом деле, 2 теоремы:1. Если система аксиом непротиворечива, то в ней
существует недоказуемое и неопровержимое
утверждение.
2. Если система аксиом непротиворечива, то в ней
нельзя вывести утверждение, доказывающее эту
непротиворечивость.
Иначе говоря, мы не можем доказать
непротиворечивость системы средствами ее самой и
мы всегда будем иметь неопределенные утверждения
(или вопросы без ответов)
12.
Лекция 1КОНЕЦ