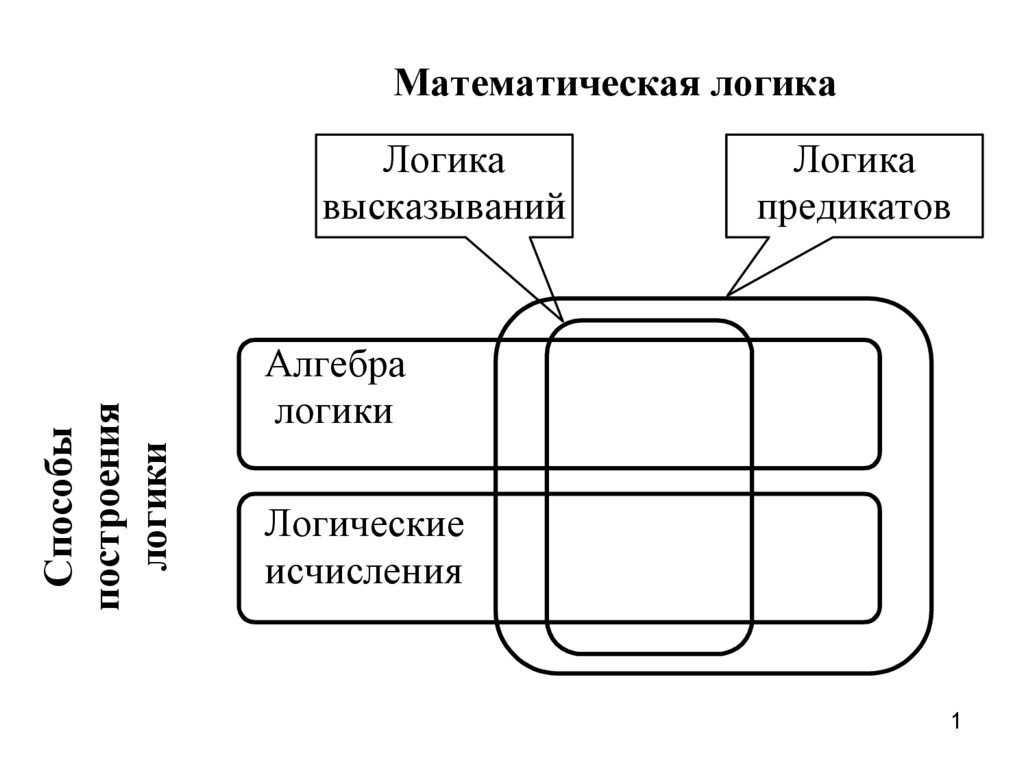
Математическая логика

1.

Математическая логика
Способы
построения
логики
Логика
высказываний
Логика
предикатов
Алгебра
логики
Логические
исчисления
1

2.

Логика высказываний
Высказывание – языковое предложение, о котором имеет смысл говорить, что оно истинно
или ложно.
В логике высказываний интересуются не содержанием, а истинностью или ложностью высказываний.
Простое высказывание – высказывание, в котором нельзя выделить часть, являющуюся высказыванием, кроме самого этого целого. Сложным (составным) называется высказывание,
составленное с помощью логических связок других высказываний.
P – отрицание (инверсия) высказывания P
P Q – конъюнкция (операция «И», логическое произведение)
P Q – дизъюнкция (операция «ИЛИ», логическая сумма)
P Q – импликация (логическое следование). Высказывание P называется посылкой импликации, а высказывание Q – заключением.
P Q – эквивалентность (эквиваленция, равнозначность).
P Q – неравнозначность (исключающее «ИЛИ», сложение по модулю 2).
Алфавит логики высказываний: высказывательные переменные – обычно заглавные латинские буквы; логические символы , , , , , ; символы скобок (, ).
Последовательность символов в логике высказываний называется формулой, если она удовлетворяет следующему определению:
1) любая высказывательная переменная – формула;
2) если A и B – формулы, то A, A B, A B, A B, A B, A B, (A) – формулы;
2

3.

Применение к естественному языку
В формальной логике изучается строение сложных логических высказываний,
выраженных формулами, вне зависимости от содержания составляющих их простых
высказываний.
Содержательных интерпретаций у любой формулы бесконечно много.
В обычном языке мы не употребляем скобок для указания того, как нужно сочетать
различные части сложной фразы, используя иногда взамен довольно тонкие средства.
Перевод обычного языка в логические символы не является механическим делом:
«Если Джонс присутствует (Д) или если Уильямс выскажется за наше
предложение (У) и Старк не станет возражать (С), то наше предложение
будет принято (П)»
Как надо переводить?
а) (Д У) С П
б) Д (У С) П.
В письменном языке отсутствие запятой перед «и» решит в пользу (в); в устной же
речи, чтобы выразить именно (а), надо заменить «и» на «ну и конечно, если».
3

4.

В логике высказываний A B равносильно B A, фразы:
«у Джейн родился ребенок, и она вышла замуж»,
«Джейн вышла замуж, и у нее родился ребенок»
будут пониматься знакомыми Джейн по-разному. В этом примере порядок высказываний в конъюнкции наводит на мысль о следовании во времени или о причинноследственной связи.
Следование во времени можно выразить с помощью классической логики, если
пользоваться символизмом исчисления предикатов.
«Сегодня понедельник или вторник» = A B.
A – «Сегодня понедельник»; B – «Сегодня вторник».
«Идет дождь или снег» = A B
A – «Идет дождь»; B – «Идет снег».
Если известно или неявно предполагается (A B), то включительное и исключительное «A или B» равносильны и можно употреблять перевод A B.
«n – четное (A) или нечетное простое число (B)»:
A B для математической аудитории,
(A B) (A B) для аудитории, не знающей, что число не может быть чётным и
нечётным одновременно.
4

5.

Список наиболее часто встречающихся выражений,
соответствующих логическим связкам
A B
AиB
Не только A, но и B
B, несмотря на A
Как A, так и B
A вместе с B
A, в то время как B
A B
Если A, то B
Коль скоро A, то B
В случае A имеет место B
Для B достаточно A
Для A необходимо B
A, только если B
B, если A
A влечет B
A имплицирует B
A, если и только если B
Если A, то B, и обратно
A, если B, и B, если A
Для A необходимо и
A B
достаточно B
A равносильно B
A тогда и только тогда,
когда B
A B
A
A или B, или оба
A или B
A, если не B
A и/или B (в юридических
текстах)
Не A (или то, что получится в
результате вставки частицы
"не" перед глаголом –
основным или
вспомогательным)
A не имеет места
A не верно
(A B)
Ни A, ни B
A B
A либо B, но не оба
Или A, или B
Либо A, либо B [иногда]
A, если не B [иногда]
A, кроме случая, когда B
[иногда]
A или B [иногда]
5

6.

Пусть N , P, D обозначают следующие высказывания
N =”Ему нравятся фиолетовые галстуки“,
P =”Он популярен“, D =”У него странные друзья“
Записать в виде высказываний символические выражения:
P D , N P D , N P D , N P P D .
Проверить правильность умозаключений:
1) Если первое, то второе.
Следовательно, если второе, то первое.
3) Если первое, то второе. Но первое неверно.
Значит, второе тоже неверно.
6

7.

Четыре подруги Маша, Полина, Ольга и Наташа участвовали
в соревнованиях по бегу и заняли первые четыре места. Установите,
кто какое место из них занял, если известно, что в каждом из приведенных ниже ответов, которые дали лукавые девушки опоздавшему
к финишу корреспонденту, верной является лишь его половина.
Н а т а ш а : Ольга была второй, а Полина – третьей.
М а ш а : Нет, Наташа. Ольга была первой, а второй была ты.
О л ь г а : Да, что вы, девочки! Второй была Маша, а Полина прибежала четвертой.
7

8.

1. Переведите каждое из следующих рассуждений в логическую символику и проанализируйте результат на правильность:
2) Он сказал, что придет, если не будет
дождя ( Д П ). Но идет дождь ( Д ). Значит,
он не придет ( П ).
Д ="идет дождь"
П ="он придет"
1) Я бы заплатил за работу по ремонту телевизора,
только если бы он стал работать ( З Р ). Он же
не работает ( Р ). Поэтому я платить не буду ( З ).
Р ="телевизор работает"
З ="я заплачу за работу по ремонту
телевизора"
7) Если 2 – простое число, то это наименьшее
простое число ( Д Н ). Если 2 – наименьшее простое
число, то 1 не есть простое число ( Н П ). Число 1
не есть простое число ( П ). Следовательно, 2 – простое число ( Д ).
Д ="2 – простое число"
Н ="2 – наименьшее
простое число"
П ="1 не есть простое число"
9

9.

Формальные аксиоматические теории
Формальная аксиоматическая теория:
1) алфавит – некоторое счётное множество символов теории Т;
2) формулы – подмножество выражений (последовательностей символов)) теории Т;
3) аксиомы – подмножество формул теории Т;
4) правила вывода – конечное множество R1, R2, ..., Rm отношений между формулами.
Если A и формулы A1, A2, ..., Ai находятся в некотором отношении Rk (1 k m ), то
A –непосредственное следствие из формул A1, A2, ..., Ai, полученное по правилу Rk.
Выводом в теории Т называется последовательность 1, 2, ..., n формул такая, что i 1, n
i – либо аксиома теории Т, либо непосредственное следствие каких-либо предыдущих
формул.
Формула A называется теоремой теории Т, если в ней существует вывод, в котором
последней формулой является A.
Формула A называется следствием множества формул Г тогда и только тогда, когда
существует такая последовательность формул 1, 2, ..., n, что n=A и i 1, n i – либо
аксиома, либо формула из Г, либо непосредственное следствие некоторых предыдущих
формул. Последовательность 1, 2, ..., n называется выводом A из Г. Элементы Г называются посылками вывода или гипотезами.
B1, B2, ..., Bk A
формула A выводима из формул B1, B2, ..., Bk
A
формула A доказуема, а сам вывод – доказательство.
13

10.

Формальная аксиоматическая теория называется
– полной, если в ней доказуема любая тавтология.
– непротиворечивой, если в ней не существует вывода формулы A
такой, что одновременно доказуемы формулы A и A.
– полной в узком смысле, если добавление любой невыводимой формулы в качестве схемы аксиом приводит к противоречивой системе.
14

11.

Исчисление высказываний (ИВ)
1. Алфавит ИВ образуют буквы A, B, C... и т.д. (возможно с индексами), которые называются
пропозициональными переменными, логические символы (связки) , , , , а также вспомогательные символы скобок (, ).
2. Множество формул ИВ определяется индуктивно:
а) все пропозициональные переменные являются формулами ИВ;
б) если A и B формулы ИВ, то ( A), (A B), (A B), (A B) – формулы ИВ;
в) выражение является формулой ИВ тогда и только тогда, когда это может быть установлено
с помощью пунктов а) и б).
Внешние скобки у формул обычно опускают
3. Аксиомы ИВ (система Клини).
1) A (B A)
2) (A B) ((A (B C)) (A C))
3) A (B A B)
4) A B A
5) A B B
6) A A B
7) B A B
8) (A C) ((B C) (A B C))
9) (A B) ((A B) A)
10) A A
A, A B
.
B
Выводом A1, A2,..., An – A называется последовательность формул 1, 2,..., m, A, в которой любая
формула либо является одной из формул A1, A2,..., An (т.е. посылкой), либо аксиомой, либо подстановкой в аксиому, либо получается из предыдущих формул по правилу вывода.
4. Правило вывода в ИВ единственное – правило заключения (modus ponens):
Исчисление высказываний – непротиворечивая, полная аксиоматическая теория, причем ИВ полно
и в узком смысле.
15

12.

I. Построить вывод D C D
1) D
посылка,
2) D C D аксиома 7, A C, B D,
3) C D
m.p. 1 и 2.
1) A (B A)
2) (A B) ((A (B C)) (A C))
7) B A B
II. Построить вывод A B, B C A C
1) A B
посылка,
2) (A B) ((A (B C)) (A C)) аксиома 2,
3) (A (B C)) (A C)
m.p. 1 и 2,
4) B C
посылка,
5) (B C) (A (B C))
аксиома 1, A B C, B A,
6) (A (B C))
m.p. 4 и 5.
7) A C
m.p. 6 и 3.
III. Доказать D D
1) D (D D)
2) (D (D D)) ((D ((D D) D)) (D D))
3) (D ((D D) D)) (D D)
4) D ((D D) D)
5) D D
акс. 1, A D, B D,
акс. 2, A D, B D D, C D,
m.p. 1 и 2,
акс. 1, A D, B D D,
m.p. 4 и 3.
16

13.

Теорема о дедукции. Если имеется вывод ,A B, то можно построить вывод A B,
где – набор некоторых формул A1, A2,..., An.
Пусть последовательность формул 1, 2,..., m, B, является выводом , A B. Этот вывод
далее будем называть вспомогательным.
Цель алгоритма: получить последовательность формул A 1,..., A 2,..., A m,..., A B,
являющуюся выводом.
Возможны случаи:
1) i – аксиома или подстановка в аксиому;
2) i – одна из посылок A1, A2,..., An;
3) i=A;
4) i – modus ponens x и y, где x<i, y<i, причем y= x i.
Рассмотрим для каждого из 4-х случаев, на какую последовательность формул нужно
заменить i.
Случаи 1 и 2:
Случай 3:
1) i ,
1) A (A A) акс. 1, B A,
2) i (A i)
акс. 1 A i, B A,
2) (A (A A)) ((A ((A A) A)) (A A))
3) A i m.p. 1 и 2.
акс. 2, B A A, C A,
3) (A ((A A) A)) (A A) m.p. 1 и 2,
4) A ((A A) A) акс. 1, B A A,
5) A A m.p. 4 и 3.
Случай 4:
Пусть i – modus ponens x и y, где x<i, y<i, причем y= x i. Пусть также в результирующем выводе формула A x имеет номер p, а формула A ( x i) имеет номер q.
1) (A x) ((A ( x i)) (A i)) акс.2, A A, B x, C i ,
2) (A ( x i)) (A i) m.p. p и 1,
17
3) A i m.p. q и 2.

14.

Пример. Построить вывод A B B A.
A
B
0
B A
A B
((A B) ( B A))
0
1
1
1
1
1
0
1
0
1
1
1
1
1
0
1
0
0
0
1
1
1
0
0
1
1
1
B
A
Формула ((A B) ( B A)) – ТИФ, следовательно, вывод существует.
18

15.

19