лекц_14 ДМ-4 (и практ 24) на 26.12.25 =

1.

Национальный исследовательский
Томский политехнический университет
Механика 1.3
3.09 .25;
Лектор - Козлов Виктор Николаевич,
доцент отделения машиностроения ИШНПТ
моб. тел. +7-913-812-58-34, kovn@tpu.ru
ВКС 380 440 5794, Пароль: 1DepTr
Лекции – 24 часа,
практические занятия – 32 часа,
88 часов самостоятельной работы,
расчётно-графические работы (РГР)
всего 144 ч., 4 кредита. Экзамен
1

2.

4.4 Передаточные механизмы (продолжение 45)
.
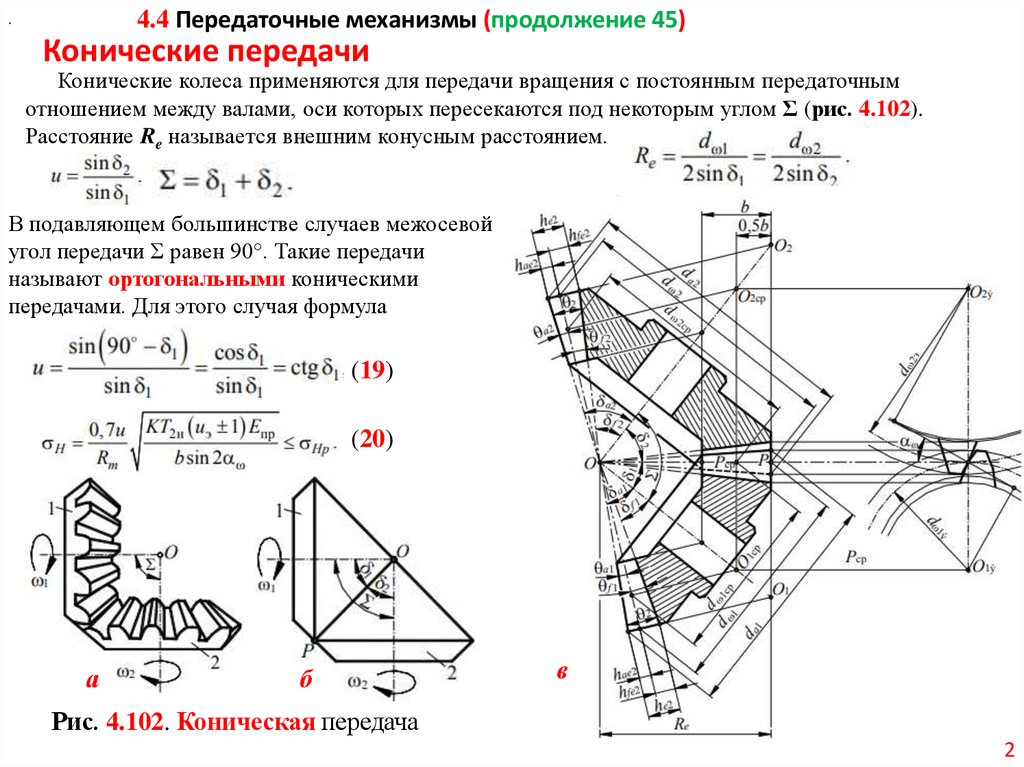
Конические передачи
Конические колеса применяются для передачи вращения с постоянным передаточным
отношением между валами, оси которых пересекаются под некоторым углом Ʃ (рис. 4.102).
Расстояние Re называется внешним конусным расстоянием.
В подавляющем большинстве случаев межосевой
угол передачи Ʃ равен 90°. Такие передачи
называют ортогональными коническими
передачами. Для этого случая формула
(19)
(20)
а
б
в
Рис. 4.102. Коническая передача
2

3.

.
4.4 Передаточные механизмы (продолжение 46)
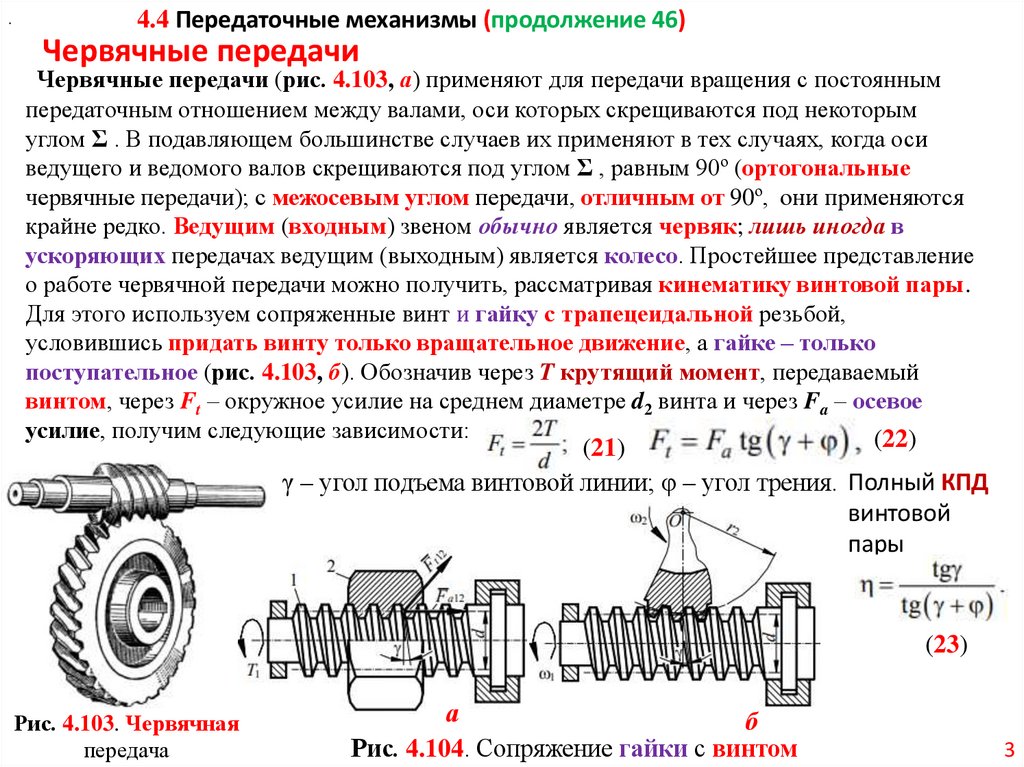
Червячные передачи
Червячные передачи (рис. 4.103, а) применяют для передачи вращения с постоянным
передаточным отношением между валами, оси которых скрещиваются под некоторым
углом Ʃ . В подавляющем большинстве случаев их применяют в тех случаях, когда оси
ведущего и ведомого валов скрещиваются под углом Ʃ , равным 90º (ортогональные
червячные передачи); с межосевым углом передачи, отличным от 90º, они применяются
крайне редко. Ведущим (входным) звеном обычно является червяк; лишь иногда в
ускоряющих передачах ведущим (выходным) является колесо. Простейшее представление
о работе червячной передачи можно получить, рассматривая кинематику винтовой пары.
Для этого используем сопряженные винт и гайку с трапецеидальной резьбой,
условившись придать винту только вращательное движение, а гайке – только
поступательное (рис. 4.103, б). Обозначив через T крутящий момент, передаваемый
винтом, через Ft – окружное усилие на среднем диаметре d2 винта и через Fa – осевое
усилие, получим следующие зависимости:
(22)
(21)
γ – угол подъема винтовой линии; φ – угол трения. Полный КПД
винтовой
пары
(23)
Рис. 4.103. Червячная
передача
а
б
Рис. 4.104. Сопряжение гайки с винтом
3

4.

.
4.4 Передаточные механизмы (продолжение 47)
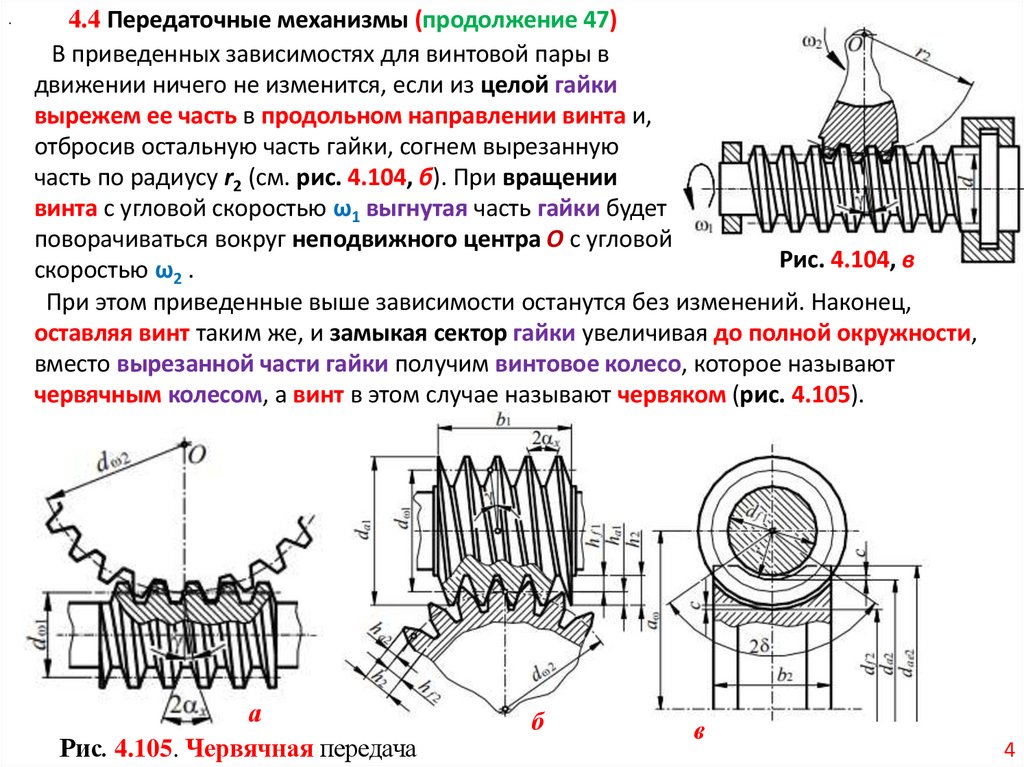
В приведенных зависимостях для винтовой пары в
движении ничего не изменится, если из целой гайки
вырежем ее часть в продольном направлении винта и,
отбросив остальную часть гайки, согнем вырезанную
часть по радиусу r2 (см. рис. 4.104, б). При вращении
винта с угловой скоростью ω1 выгнутая часть гайки будет
поворачиваться вокруг неподвижного центра О с угловой
Рис. 4.104, в
скоростью ω2 .
При этом приведенные выше зависимости останутся без изменений. Наконец,
оставляя винт таким же, и замыкая сектор гайки увеличивая до полной окружности,
вместо вырезанной части гайки получим винтовое колесо, которое называют
червячным колесом, а винт в этом случае называют червяком (рис. 4.105).
а
Рис. 4.105. Червячная передача
б
в
4

5.

4.4 Передаточные механизмы (продолжение 48)
.
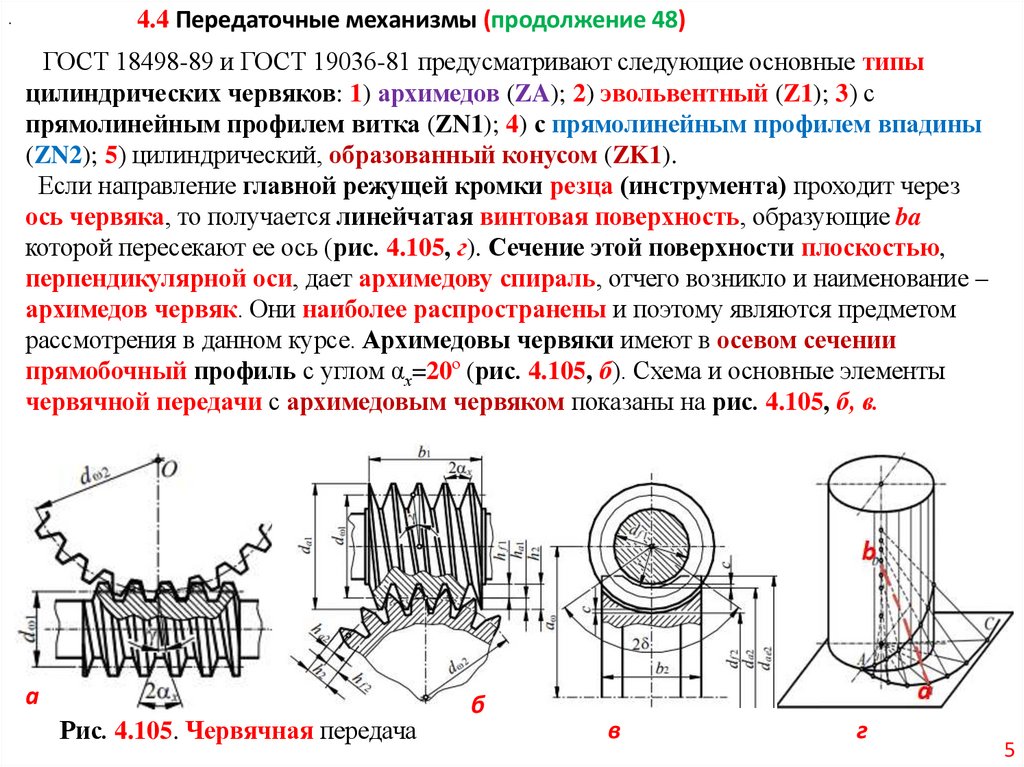
ГОСТ 18498-89 и ГОСТ 19036-81 предусматривают следующие основные типы
цилиндрических червяков: 1) архимедов (ZA); 2) эвольвентный (Z1); 3) с
прямолинейным профилем витка (ZN1); 4) с прямолинейным профилем впадины
(ZN2); 5) цилиндрический, образованный конусом (ZK1).
Если направление главной режущей кромки резца (инструмента) проходит через
ось червяка, то получается линейчатая винтовая поверхность, образующие ba
которой пересекают ее ось (рис. 4.105, г). Сечение этой поверхности плоскостью,
перпендикулярной оси, дает архимедову спираль, отчего возникло и наименование –
архимедов червяк. Они наиболее распространены и поэтому являются предметом
рассмотрения в данном курсе. Архимедовы червяки имеют в осевом сечении
прямобочный профиль с углом αх=20º (рис. 4.105, б). Схема и основные элементы
червячной передачи с архимедовым червяком показаны на рис. 4.105, б, в.
а
Рис. 4.105. Червячная передача
б
в
г
5

6.

.
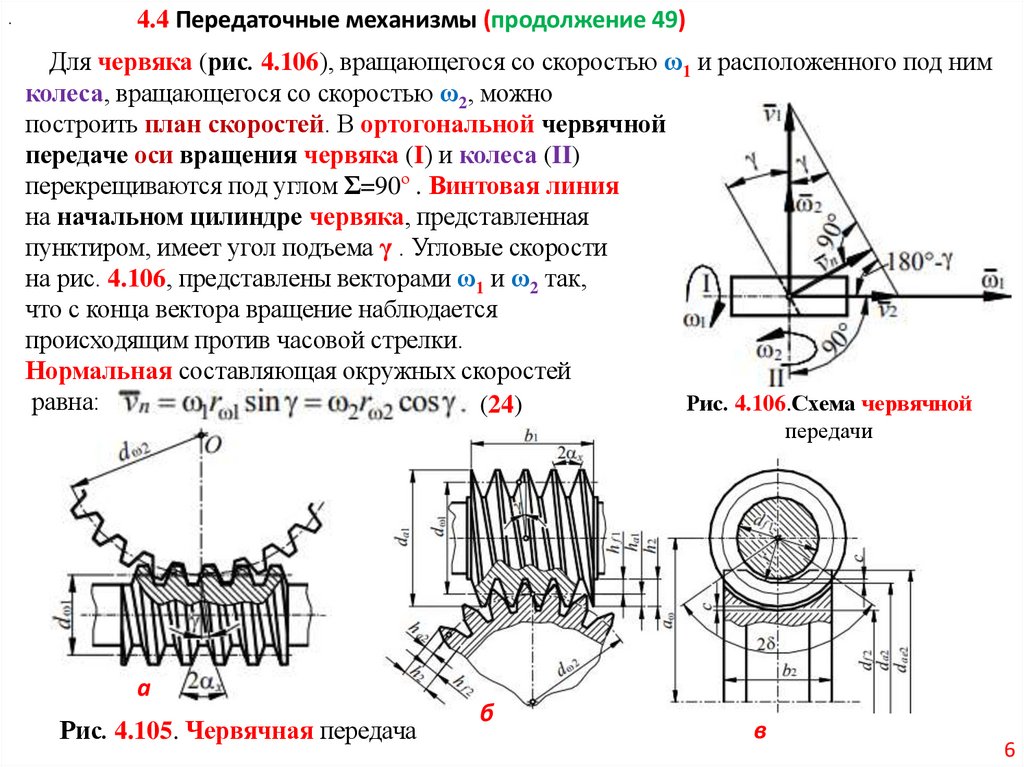
4.4 Передаточные механизмы (продолжение 49)
Для червяка (рис. 4.106), вращающегося со скоростью ω1 и расположенного под ним
колеса, вращающегося со скоростью ω2, можно
построить план скоростей. В ортогональной червячной
передаче оси вращения червяка (I) и колеса (II)
перекрещиваются под углом Ʃ=90º . Винтовая линия
на начальном цилиндре червяка, представленная
пунктиром, имеет угол подъема γ . Угловые скорости
на рис. 4.106, представлены векторами ω1 и ω2 так,
что с конца вектора вращение наблюдается
происходящим против часовой стрелки.
Нормальная составляющая окружных скоростей
равна:
Рис. 4.106.Схема червячной
(24)
передачи
а
Рис. 4.105. Червячная передача
б
в
6

7.

.
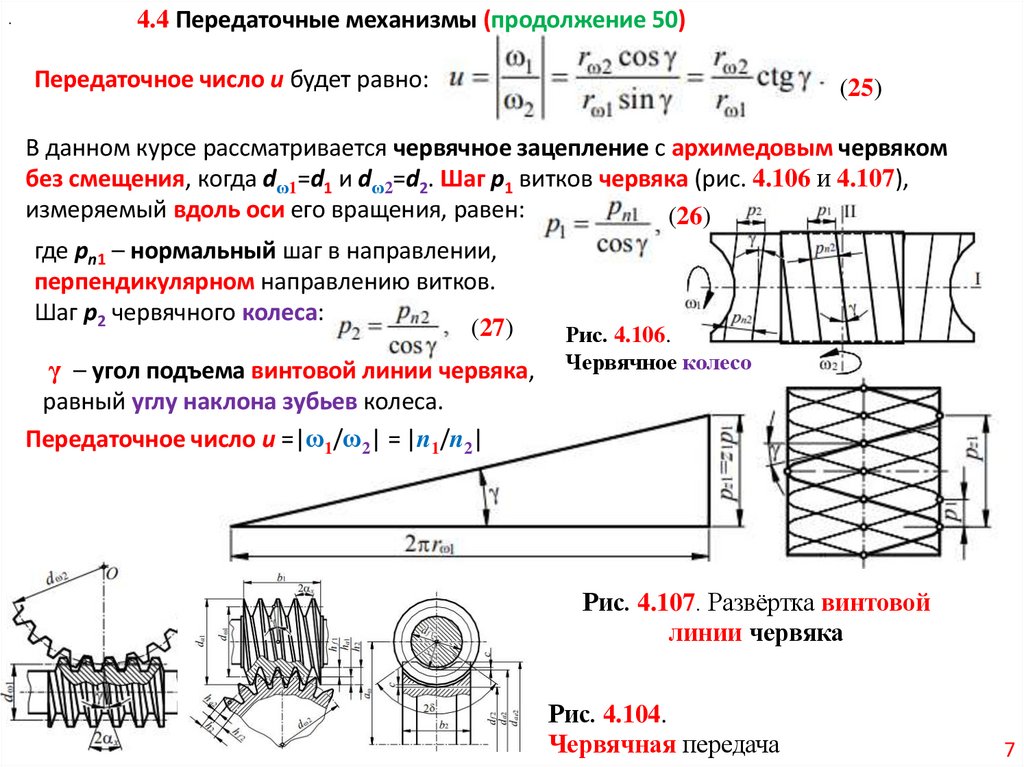
4.4 Передаточные механизмы (продолжение 50)
Передаточное число u будет равно:
(25)
В данном курсе рассматривается червячное зацепление с архимедовым червяком
без смещения, когда dω1=d1 и dω2=d2. Шаг p1 витков червяка (рис. 4.106 и 4.107),
измеряемый вдоль оси его вращения, равен:
(26)
где pn1 – нормальный шаг в направлении,
перпендикулярном направлению витков.
Шаг p2 червячного колеса:
(27)
Рис. 4.106.
γ – угол подъема винтовой линии червяка,
равный углу наклона зубьев колеса.
Передаточное число u =|ω1/ω2| = |n1/n2|
Червячное колесо
Рис. 4.107. Развёртка винтовой
линии червяка
Рис. 4.104.
Червячная передача
7

8.

.
4.4 Передаточные механизмы (продолжение 51)
В зависимости от направления резьбы червяка различают правозаходные
(преимущественно распространенные) и левозаходные передачи. В зависимости от
количества параллельных витков резьбы червяка различают передачи
однозаходные и многозаходные (как правило, z1 <4 ). Из уравнений (26) и (27),
вследствие равенства нормальных шагов червяка и червячного колеса, следует, что
p1= p2= p. Ход винтовой линии червяка pz1 равен pz1 =2π∙rω1∙tg γ = z1∙p, где z1 – число
заходов червяка. С учетом того, что модуль m=p/π , радиус начальной окружности
червяка будет равен:
(28)
Для упрощения расчетных формул введем коэффициент, называемый относительным
диаметром червяка q :
Для червяка:
Для червячного колеса:
(29)
8

9.

.
4.4 Передаточные механизмы (продолжение 52)
Для проектирования ортогональной червячной передачи с архимедовым
червяком без смещения на основании опыта их проектирования, изготовления и
эксплуатации предложены следующие рекомендации. Длина нарезанной части
червяка b1 : при z1 , равном 1 и 2:
при z1 , равном 3 и 4:
Ширина колеса b2 при z1 <4 :
Наибольший диаметр червячного колеса:
Условный угол обхвата 2δ:
для силовых передач 2δ =90°-120°, для кинематических передач 2δ=45°-90°.
Коэффициент полезного действия червячной передачи определяется как КПД
последовательной цепи звеньев:
где ηвп — КПД винтовой кинематической пары, соответствующий подъему гайки по
винту; ηзз – КПД зубчатого зацепления (0,97-0,98).
Скорость скольжения зубьев колеса по виткам червяка определяется как разность
векторов окружных скоростей этих элементов:
КПД передачи возрастает с увеличением числа витков (заходов) червяка z1 (при этом
увеличивается угол подъема винтовой линии γ) и с уменьшением коэффициента трения f . Как
показали экспериментальные исследования, КПД зацепления зависит и от шероховатости
поверхности, увеличиваясь с ее уменьшением.
9

10.

.
4.4 Передаточные механизмы (продолжение 52)
Невысокий КПД показывает то, что в червячной передаче значительная часть
механической энергии переходит в тепловую. Вызванное этим повышение температуры
зоны контакта ухудшает защитные свойства масляного слоя, увеличивает опасность
заедания и выхода передачи из строя. Для предотвращения чрезмерного повышения
температуры масла рассматривают тепловой баланс между тепловыделением и
теплоотдачей и при необходимости реализуют мероприятия, уменьшающие
тепловыделение выделение или увеличивающие теплоотдачу (ставят радиаторы).
Основные достоинства червячных передач – большое передаточное число
(отношение) в одной ступени, плавность и относительная бесшумность, возможность
самоторможения (при низком коэффициенте полезного действия).
Основные недостатки – низкий КПД, нагрев при работе на машинах непрерывного
действия, высокая стоимость материала венцов червячных колес (бронза) для
быстроходных передач.
Передаточное число:
Передаточное отношение червячной передачи:
i12=ω1/ω2 = n1/n2 = где k – число заходов червяка (1-3),
z = z2 – число зубьев червячного
=z2/z1= z2/ k .
колеса (28-80).
Передаточное число: u = n1 /n2 = z2/z1 , где n1 – число оборотов червяка;
n2 – число оборотов червячного колеса, z2 – число зубьев червячного
колеса, z1 (k) – число заходов червяка.
10

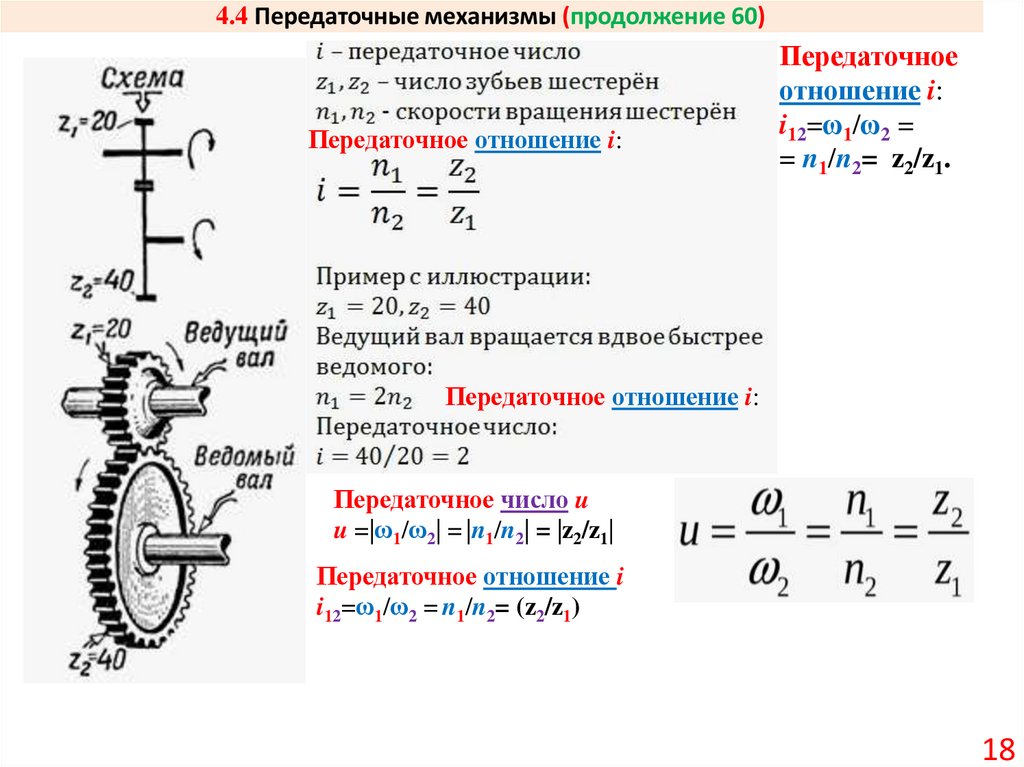
11. 4.4 Передаточные механизмы (продолжение 53)

Передаточное число u =|ω1/ω2| = |n1/n2| .
Передаточное отношение i12=ω1/ω2 = n1/n2.
11

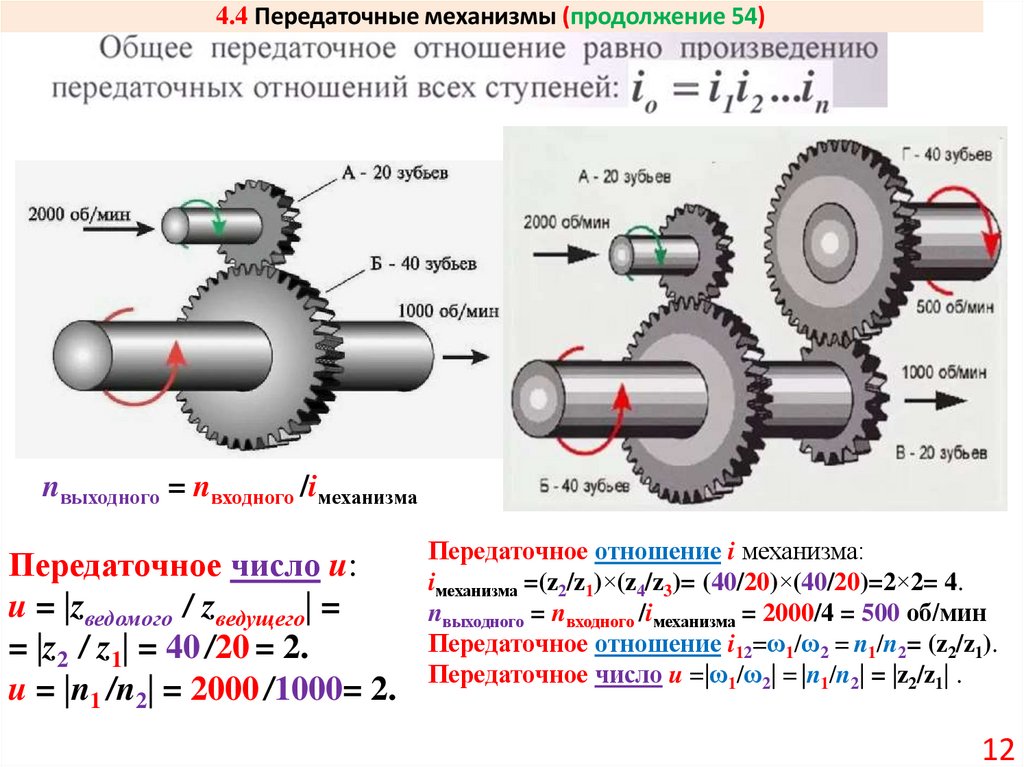
12. 4.4 Передаточные механизмы (продолжение 54)

nвыходного = nвходного /iмеханизма
Передаточное число u:
u = |zведомого / zведущего| =
= |z2 / z1| = 40 /20 = 2.
u = |n1 /n2| = 2000 /1000= 2.
Передаточное отношение i механизма:
iмеханизма =(z2/z1)×(z4/z3)= (40/20)×(40/20)=2×2= 4.
nвыходного = nвходного /iмеханизма = 2000/4 = 500 об/мин
Передаточное отношение i12=ω1/ω2 = n1/n2= (z2/z1).
Передаточное число u =|ω1/ω2| = |n1/n2| = |z2/z1| .
12

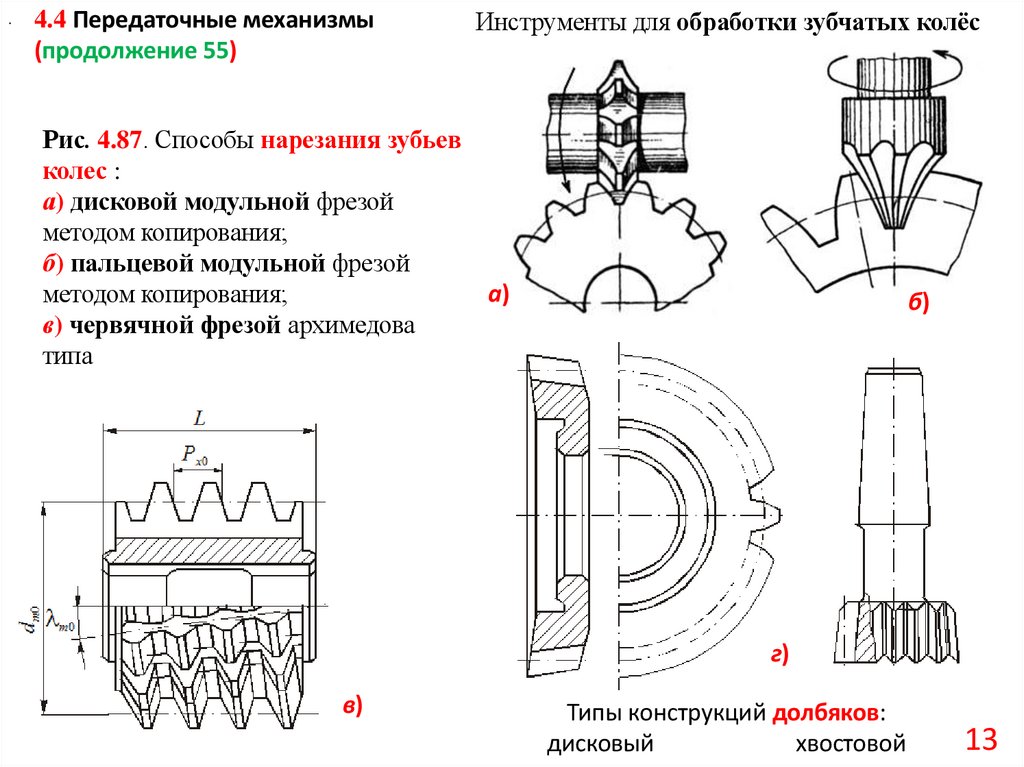
13. Инструменты для обработки зубчатых колёс

.
4.4 Передаточные механизмы
(продолжение 55)
Рис. 4.87. Способы нарезания зубьев
колес :
а) дисковой модульной фрезой
методом копирования;
б) пальцевой модульной фрезой
методом копирования;
в) червячной фрезой архимедова
типа
Инструменты для обработки зубчатых колёс
а)
б)
г)
в)
Типы конструкций долбяков:
дисковый
хвостовой
13

14.

.
4.4 Передаточные механизмы (продолжение 56)
Выбор материала зубчатых колес (обычно
сталь 40Х) определяется назначением передачи,
условиями ее работы (режим нагрузки,
температура, смазка и пр.), способом получения
заготовок, методом изготовления и обработки
зубьев. Стремление к снижению массы и
габаритов силовых зубчатых передач
определило широкое применение сталей,
Рис. 4.88. Фрезерование зубчатого венца
подвергнутых термическому или химикочервячной фрезой.
термическому упрочнению, которые допускают
Обычно черновое нарезание зубчатых колес
производят за один рабочий ход, но если мощность
возможность получения высокой твердости
станка оказывается недостаточной, то нарезание
рабочих поверхностей зубьев при большой
следует производить за два рабочих хода с глубиной
прочности и вязкости сердцевины (при нагреве резания на первом ходу 1,4, а на втором 0,7 от
перед закалкой токами высокой частоты (ТВЧ). модуля.
Термообработка металлов – процесс тепловой обработки металлов и сплавов с
целью изменения их структуры, а, следовательно, и свойств, заключающийся в
нагреве до определенной температуры, выдержке при этой температуре и
последовательном охлаждении с заданной скоростью. Наиболее распространенными
видами термообработки являются нормализация (нагрев, выдержка и последующее
охлаждение на спокойном воздухе), закалка (нагрев, выдержка и последующее резкое
охлаждение), улучшение (закалка стали и последующий высокий отпуск – нагрев до (500–
680)°С и последующее медленное или быстрое охлаждение). Выбор способа термообработки
зубчатых колес из стали зависят от требуемой несущей способности зубчатых колес, марки
стали, оборудования и трудоемкости изготовления.
14

15. 4.4 Передаточные механизмы (продолжение 57)

При химико-термической обработке происходит, в основном, изменение структуры
поверхностного слоя материала, в результате чего повышаются твердость, износоустойчивость и
устойчивость против коррозии. Наиболее распространенными видами химико-термической
обработки являются цементация (насыщение поверхностного слоя углеродом) и азотирование
(насыщение поверхностного слоя азотом). В условиях индивидуального и мелкосерийного
производства, в мало и средне нагруженных передачах, а также в открытых передачах с
большими колесами применяют зубчатые колеса с твердостью материала менее или равной НВ
350. При этом обеспечивается чистовое нарезание зубьев после термообработки, высокая
точность изготовления и хорошая прирабатываемость зубьев. С целью повышения нагрузочной
способности передачи используют колеса с твердостью рабочих поверхностей зубьев HRC 40-56.
Зубья колеса нарезают на заготовке из сырой стали, а затем подвергают их термической или
химико-термической обработке (объемной закалке, поверхностной закалке, цементации с
последующей закалкой, азотированию, цианированию и т.д.). После объемной закалки и
цементации неизбежны некоторые искажения формы зубьев, которые при необходимости
исправляют шлифованием или обкаткой с применением специальных паст.
Для лучшей приработки зубьев и повышения стойкости против заедания рекомендуется
твердость зубьев шестерни назначать несколько выше твердости зубьев колеса. Для
изготовления малонагруженных или редко работающих передач, в которых габариты и масса не
имеют определяющего значения, применяют чугун. Кроме сталей и чугуна для изготовления
колес применяют также бронзы, латуни, пластмассы, реже – сплавы алюминия и магния,
керамику и др. Для уменьшения трения и повышения КПД в приборах часто применяют колеса
из латуни (например, ЛС 59-1, ЛК80-ЗЛ) или бронзы (БрОЦС 6-6-3, БрАЖ 9-4, БрАМц 9-2),
работающие в паре со стальными шестернями (трибами). Часто из медных сплавов выполняют
только венец колеса, насаживаемый на стальную ступицу.
15

16. 4.4 Передаточные механизмы (продолжение 58)

Условия работы зубьев в зацеплении и
критерии работоспособности передачи. При
трансформации крутящего момента в зацеплении
двух прямозубых колес возникает циклическая
сила нормального давления, распределенная по
контактной линии. Перекатывание зубьев
происходит со скольжением одного профиля по
другому и поэтому в зацеплении возникает
также сила трения. Потеря работоспособности
зубчатых передач: 1) поломка зубьев — наиболее
опасный вид разрушения. Различают: —
усталостные поломки, возникающие вследствие
изгибных повторно-переменных напряжений в
зубьях, когда при многократном повторении
нагрузки создается напряжение, превышающее
предел выносливости материала, и у основания
зуба возникает и распространяется усталостная
трещина; увеличивают жесткость валов,
применяют бочкообразные зубья и др.
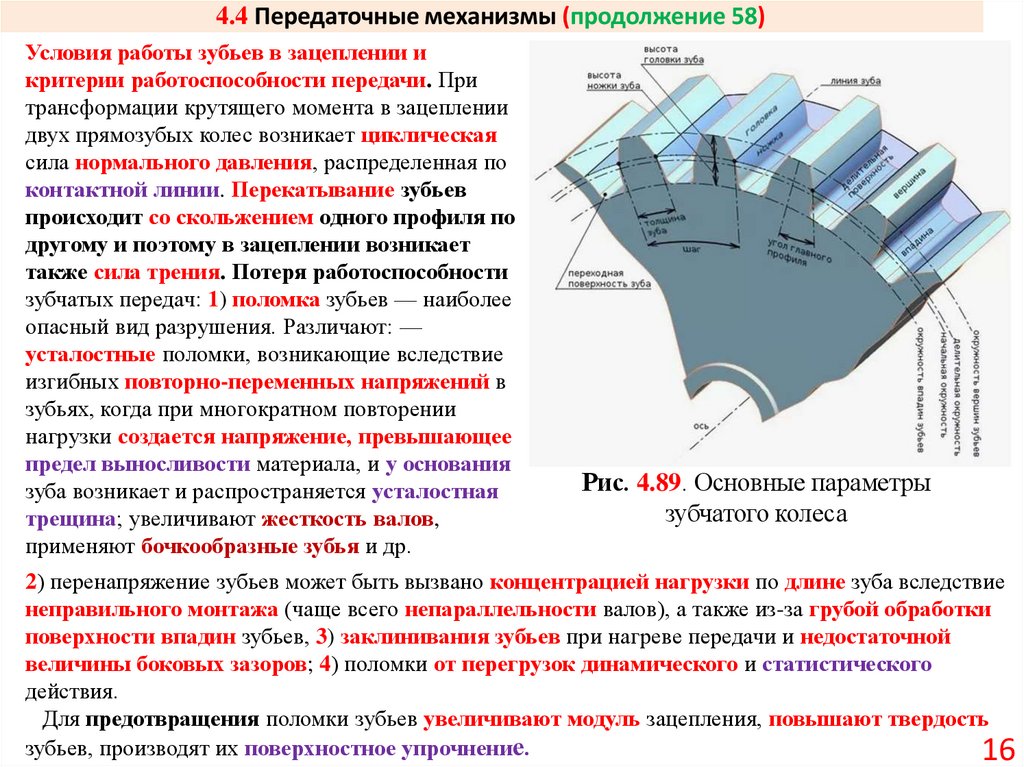
Рис. 4.89. Основные параметры
зубчатого колеса
2) перенапряжение зубьев может быть вызвано концентрацией нагрузки по длине зуба вследствие
неправильного монтажа (чаще всего непараллельности валов), а также из-за грубой обработки
поверхности впадин зубьев, 3) заклинивания зубьев при нагреве передачи и недостаточной
величины боковых зазоров; 4) поломки от перегрузок динамического и статистического
действия.
Для предотвращения поломки зубьев увеличивают модуль зацепления, повышают твердость
зубьев, производят их поверхностное упрочнение.
16

17. 4.4 Передаточные механизмы (продолжение 59)

Усталостное выкрашивание рабочих
поверхностей зубьев — основной вид
разрушения закрытых передач при
наличии обильной жидкой смазки.
Если появление усталостных раковин
вызывается начальным
приработочным износом (вследствие
неточности изготовления и монтажа
колес), то по мере приработки,
заключающейся в износе и
пластической деформации
микронеровностей, концентрация
нагрузки снижается, а образовавшиеся
раковины завальцовываются. Такое
ограниченное выкрашивание
отрицательно не сказывается на работе
зубчатой передачи.
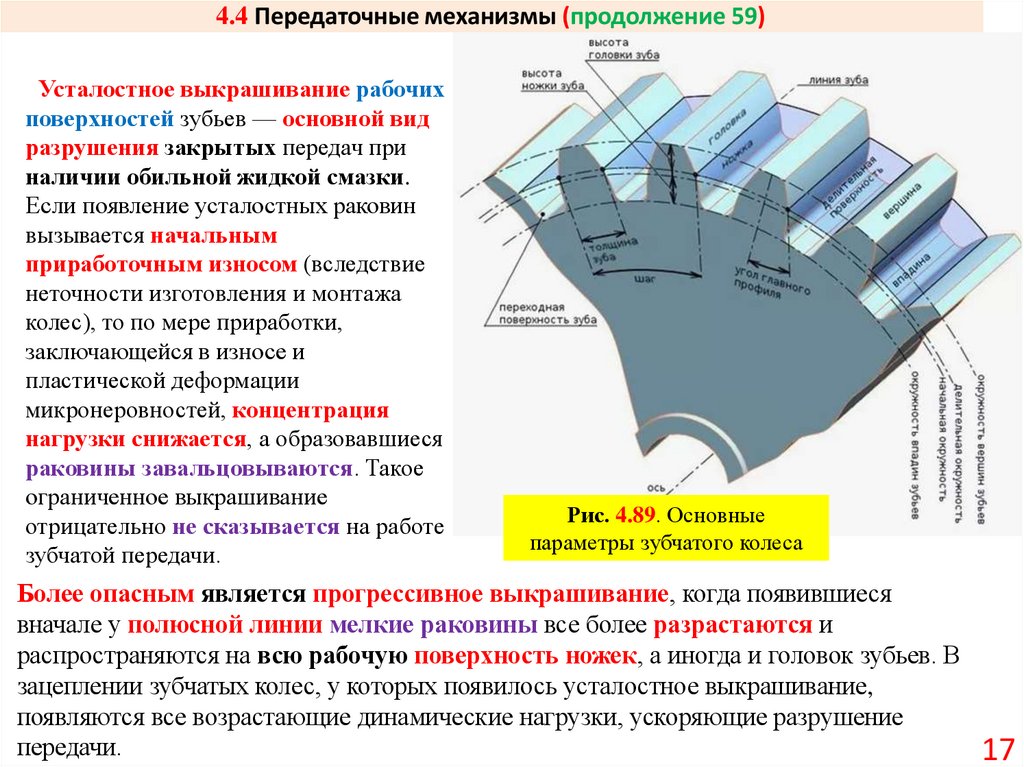
Рис. 4.89. Основные
параметры зубчатого колеса
Более опасным является прогрессивное выкрашивание, когда появившиеся
вначале у полюсной линии мелкие раковины все более разрастаются и
распространяются на всю рабочую поверхность ножек, а иногда и головок зубьев. В
зацеплении зубчатых колес, у которых появилось усталостное выкрашивание,
появляются все возрастающие динамические нагрузки, ускоряющие разрушение
передачи.
17

18. 4.4 Передаточные механизмы (продолжение 60)

Передаточное отношение i:
Передаточное
отношение i:
i12=ω1/ω2 =
= n1/n2= z2/z1.
Передаточное отношение i:
Передаточное число u
u =|ω1/ω2| = |n1/n2| = |z2/z1|
Передаточное отношение i
i12=ω1/ω2 = n1/n2= (z2/z1)
18

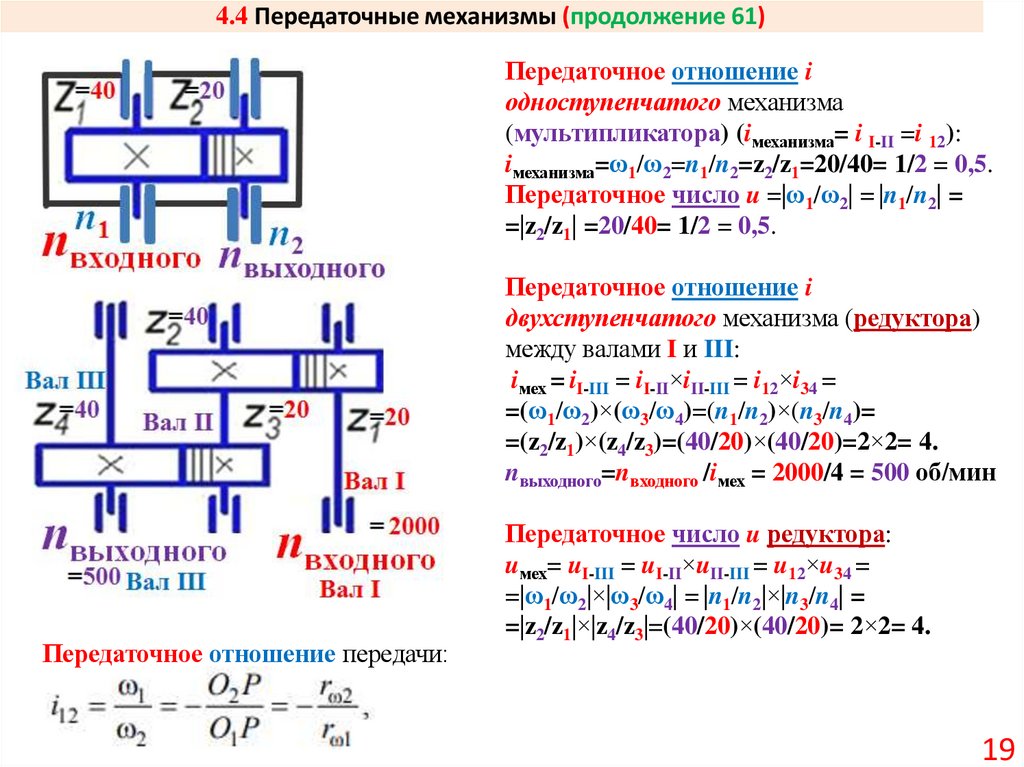
19. 4.4 Передаточные механизмы (продолжение 61)

Передаточное отношение i
одноступенчатого механизма
(мультипликатора) (iмеханизма= i I-II =i 12):
iмеханизма=ω1/ω2=n1/n2=z2/z1=20/40= 1/2 = 0,5.
Передаточное число u =|ω1/ω2| = |n1/n2| =
=|z2/z1| =20/40= 1/2 = 0,5.
Передаточное отношение i
двухступенчатого механизма (редуктора)
между валами I и III:
iмех = iI-III = iI-II×iII-III = i12×i34 =
=(ω1/ω2)×(ω3/ω4)=(n1/n2)×(n3/n4)=
=(z2/z1)×(z4/z3)=(40/20)×(40/20)=2×2= 4.
nвыходного=nвходного /iмех = 2000/4 = 500 об/мин
Передаточное отношение передачи:
Передаточное число u редуктора:
uмех= uI-III = uI-II×uII-III = u12×u34 =
=|ω1/ω2|×|ω3/ω4| = |n1/n2|×|n3/n4| =
=|z2/z1|×|z4/z3|=(40/20)×(40/20)= 2×2= 4.
19

20. 4.4 Передаточные механизмы (продолжение 62)

Множительные структуры
Регулирование скоростей главного движения осуществляется при помощи коробок
передач (скоростей). Их конструируют в виде самостоятельных узлов ,
присоединяемых к корпусу всего механизма (машины) или встроенными в
корпусные детали.
Коробки скоростей должны быть простыми и компактными, иметь малый вес,
минимальное число валов, количество передач должно быть рациональным:
1) обеспечивать достаточно широкий диапазон (например, от 12,5 до 2000 об/мин);
2) оптимальную разницу между соседними скоростями (500; 630; 800 об/мин),
3) высокий КПД; 4) низкий уровень шума.
Конструкция коробок должна быть технологичной, надежной в эксплуатации,
удобной в ремонте и обслуживании и т.д.
При проектировании коробок исходными величинами являются предельные
значения выходных параметров. Для коробок скоростей станка - это максимальная
и минимальная частота вращения шпинделя (выходного вала).
Крутящий момент на выходном вале обратно пропорционален отношению частот
вращения входного и выходного валов: чем меньше частота вращения выходного
вала по сравнению с частотой вращения входного, тем больше крутящий момент.
Как правило, частота вращения располагается по закону геометрической прогрессии.
Кроме того, он позволяет создать сложные приводы из элементарных двухвальных
механизмов, построенных на основе геометрического ряда.
n1 = nmin; n2=n1∙φ= nmin∙φ; n3 = n2∙φ = nmin∙φ∙φ = nmin∙φ2; … nm=nmin∙φm-1.
20

21. 4.4 Передаточные механизмы (продолжение 63)

n1 = nmin; n2 = n1∙φ = nmin∙φ; n3 = n2∙φ = nmin∙φ∙ φ = nmin∙φ2; … nm = nmin∙φm-1.
Обычно применяется стандартный геометрический ряд со знаменателем
геометрической прогрессии φ (φ =1,06; 1,12; 1,26; 1,41; 1,58; 1,78; 2).
Малые значения знаменателя ряда φ приводят к существенному усложнению
привода, поэтому φ = 1,06 применяется преимущественно в специальных станках.
Наибольшее применение получили значения φ = 1,26 и φ = 1,41.
Диапазон регулирования (R) частот вращения: R= nmax/nmin= φZ-1.
Количество ступеней скорости Z определяется по выражению
Cтруктуры , состоящей из элементарных двухвальных
механизмов, последовательно соединенных между собой в одну или несколько
кинематических цепей называются множительными, так как общее число скоростей
получается перемножением чисел скоростей элементарных двухвальных передач.
Схема шестиступенчатой коробки скоростей представлена на рис. 1, в которой
переключение осуществляется передвижением зубчатых блоков вдоль шлицевого вала.
Рис. 1. Схемы
шестиступенчатой
коробки скоростей
21

22.

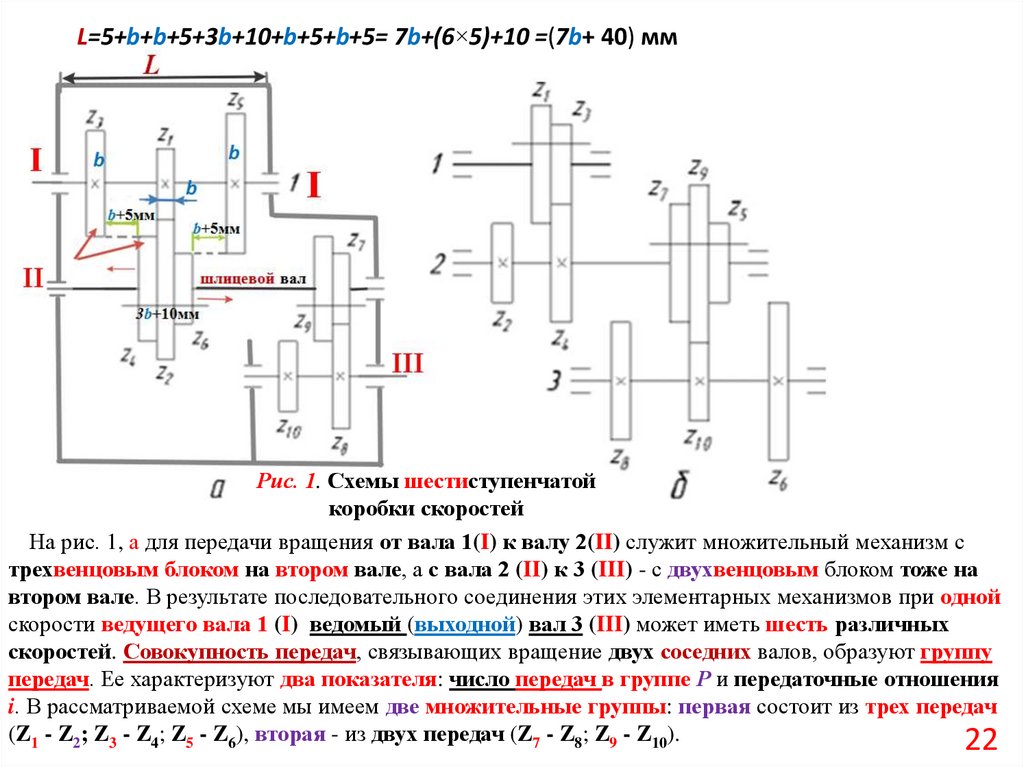
L=5+b+b+5+3b+10+b+5+b+5= 7b+(6×5)+10 =(7b+ 40) мм
Рис. 1. Схемы шестиступенчатой
коробки скоростей
На рис. 1, а для передачи вращения от вала 1(I) к валу 2(II) служит множительный механизм с
трехвенцовым блоком на втором вале, а с вала 2 (II) к 3 (III) - с двухвенцовым блоком тоже на
втором вале. В результате последовательного соединения этих элементарных механизмов при одной
скорости ведущего вала 1 (I) ведомый (выходной) вал 3 (III) может иметь шесть различных
скоростей. Совокупность передач, связывающих вращение двух соседних валов, образуют группу
передач. Ее характеризуют два показателя: число передач в группе Р и передаточные отношения
i. В рассматриваемой схеме мы имеем две множительные группы: первая состоит из трех передач
(Z1 - Z2; Z3 - Z4; Z5 - Z6), вторая - из двух передач (Z7 - Z8; Z9 - Z10).
22

23.

Рис. 1. Схемы
шестиступенчатой
коробки скоростей
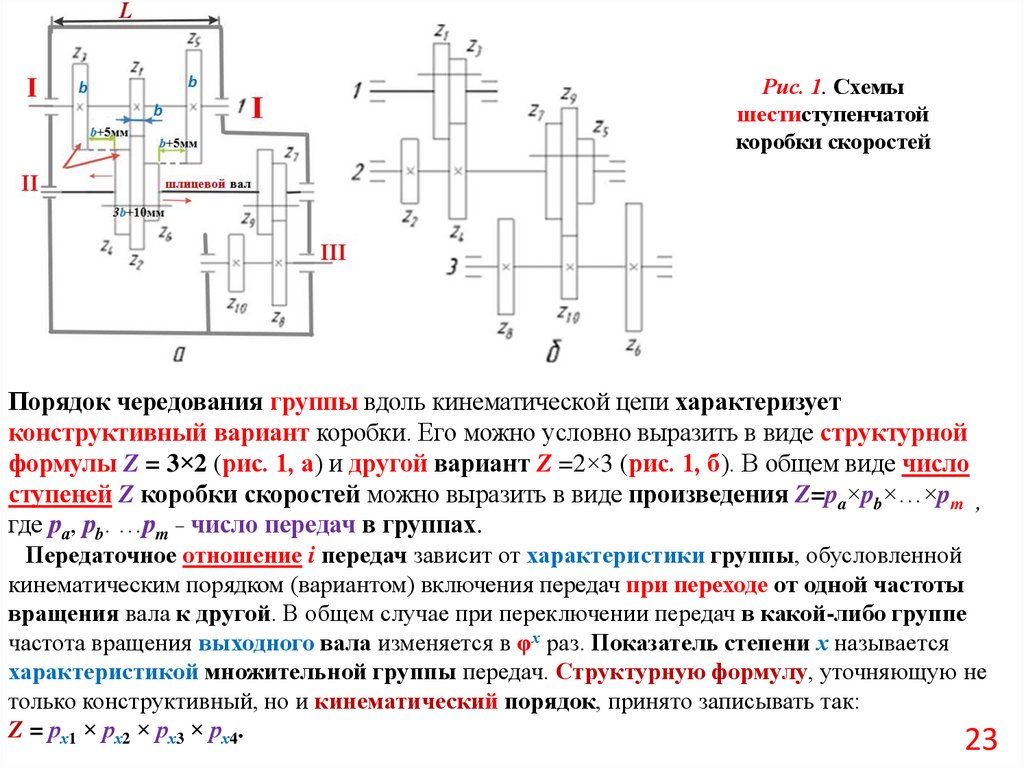
Порядок чередования группы вдоль кинематической цепи характеризует
конструктивный вариант коробки. Его можно условно выразить в виде структурной
формулы Z = 3×2 (рис. 1, а) и другой вариант Z =2×3 (рис. 1, б). В общем виде число
ступеней Z коробки скоростей можно выразить в виде произведения Z=pa×pb×…×pm ,
где ра, рb. …рm _ число передач в группах.
Передаточное отношение i передач зависит от характеристики группы, обусловленной
кинематическим порядком (вариантом) включения передач при переходе от одной частоты
вращения вала к другой. В общем случае при переключении передач в какой-либо группе
частота вращения выходного вала изменяется в φх раз. Показатель степени х называется
характеристикой множительной группы передач. Структурную формулу, уточняющую не
только конструктивный, но и кинематический порядок, принято записывать так:
Z = рх1 × рх2 × рх3 × рх4.
23

24.

Рис. 1. Схемы
шестиступенчатой
коробки скоростей
Структурную формулу,
уточняющую не только
конструктивный, но и
кинематический
порядок, принято
записывать так:
Z = рх1 × рх2 × рх3 × рх4.
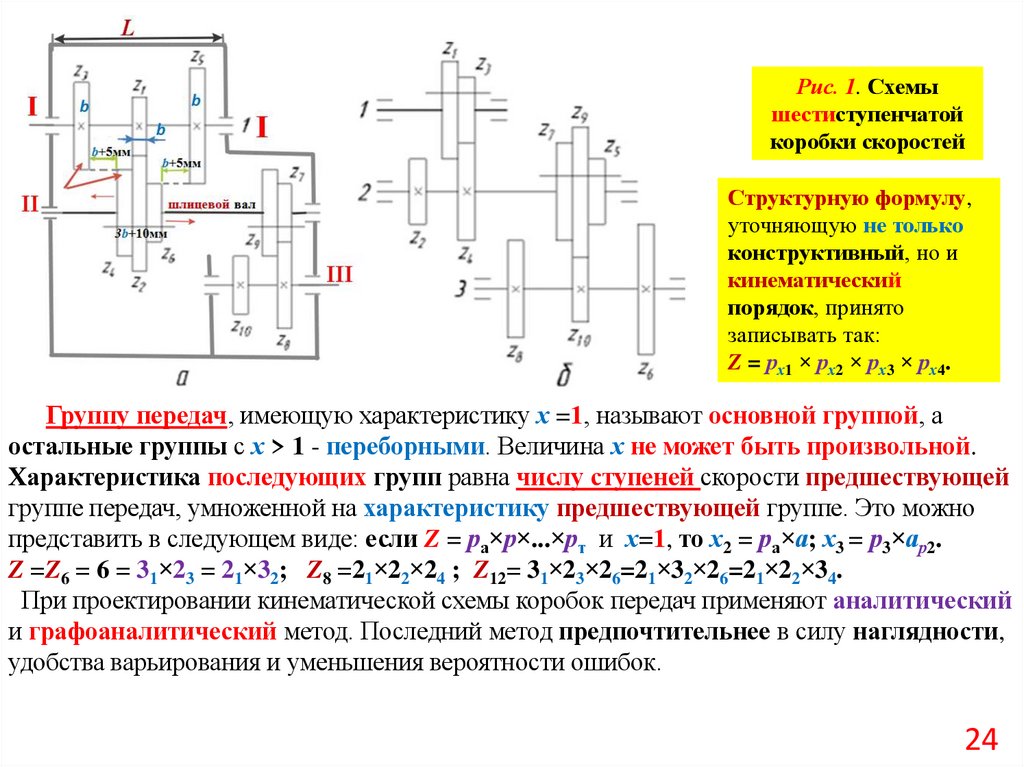
Группу передач, имеющую характеристику х =1, называют основной группой, а
остальные группы с х > 1 - переборными. Величина х не может быть произвольной.
Характеристика последующих групп равна числу ступеней скорости предшествующей
группе передач, умноженной на характеристику предшествующей группе. Это можно
представить в следующем виде: если Z = ра×р×...×рт и х=1, то х2 = ра×а; х3 = р3×ар2.
Z =Z6 = 6 = 31×23 = 21×32; Z8 =21×22×24 ; Z12= 31×23×26=21×32×26=21×22×34.
При проектировании кинематической схемы коробок передач применяют аналитический
и графоаналитический метод. Последний метод предпочтительнее в силу наглядности,
удобства варьирования и уменьшения вероятности ошибок.
24

25.

Рис. 1. Схемы
шестиступенчатой
коробки скоростей
При графоаналитическом методе аналитически
определяют диапазон регулирования частот
вращения и число ступеней коробки передач Z =
рх1×рх2×рхз... и число зубьев z1, z2 и т.д. колес в
передачах. Графическая часть метода состоит в
построении структурной сетки и графика
(картины) частот вращения с целью определения
передаточных отношений i каждой передачи.
Построение ведется на базе логарифмической шкалы. Логарифмируя выражение
nz=ni×ср-Z, получаем lgnz = lgni + (Z - l)×lgcp. Расстояние между соседними
горизонталями шкалы соответствует определенным частотам ряда n, равным
lgnk+1- lgnk = lg φ. Пусть выбрана структура Z = 6 = 31×23. В начале построения
проводим параллельно друг другу на равном расстоянии горизонтальные линии,
соответствующие валам на одну больше, чем сомножителей в формуле структуры
(число групп передач в нашем случае 2). Значит, валов будет 3. Перпендикулярно
проведенным линиям проводим вертикально Z линий (вертикальных) по числу
ступеней скорости (в нашем случае 6). Рядом записывается число передач р и
характеристика х для каждой группы.
Рис. 2. Проводим Z вертикальных
линий по числу ступеней скорости
(Z=6)
25

26.

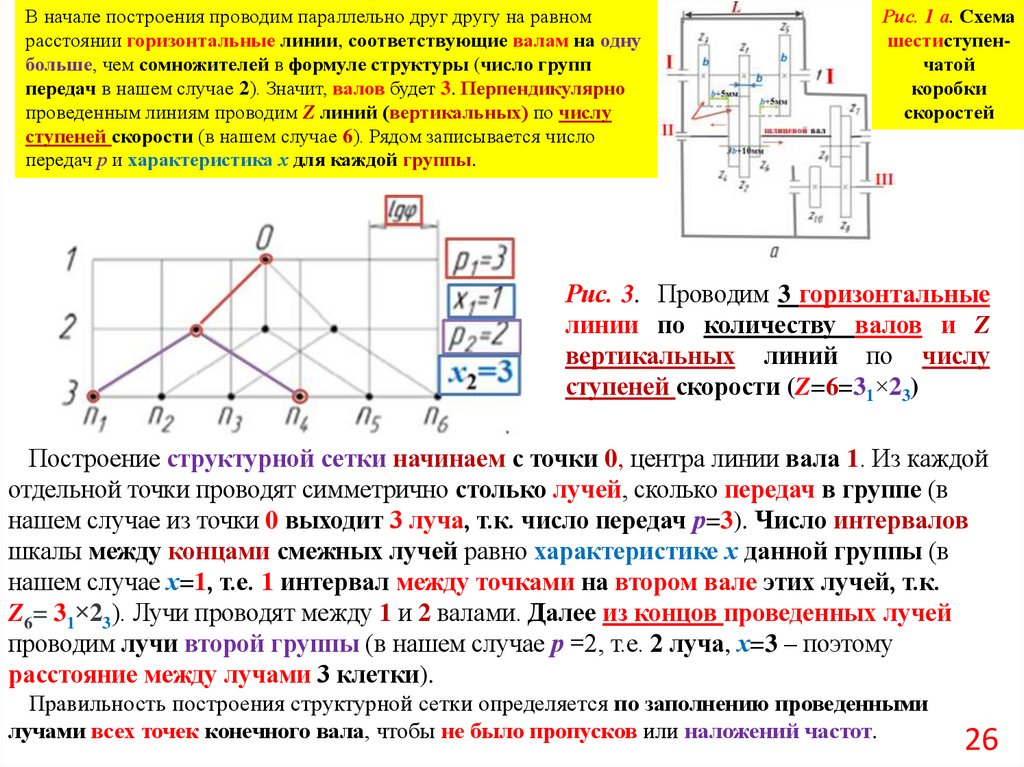
В начале построения проводим параллельно друг другу на равном
расстоянии горизонтальные линии, соответствующие валам на одну
больше, чем сомножителей в формуле структуры (число групп
передач в нашем случае 2). Значит, валов будет 3. Перпендикулярно
проведенным линиям проводим Z линий (вертикальных) по числу
ступеней скорости (в нашем случае 6). Рядом записывается число
передач р и характеристика х для каждой группы.
Рис. 1 а. Схема
шестиступенчатой
коробки
скоростей
Рис. 3. Проводим 3 горизонтальные
линии по количеству валов и Z
вертикальных линий по числу
ступеней скорости (Z=6=31×23)
Построение структурной сетки начинаем с точки 0, центра линии вала 1. Из каждой
отдельной точки проводят симметрично столько лучей, сколько передач в группе (в
нашем случае из точки 0 выходит 3 луча, т.к. число передач р=3). Число интервалов
шкалы между концами смежных лучей равно характеристике х данной группы (в
нашем случае х=1, т.е. 1 интервал между точками на втором вале этих лучей, т.к.
Z6= 31×23). Лучи проводят между 1 и 2 валами. Далее из концов проведенных лучей
проводим лучи второй группы (в нашем случае р =2, т.е. 2 луча, х=3 – поэтому
расстояние между лучами 3 клетки).
Правильность построения структурной сетки определяется по заполнению проведенными
лучами всех точек конечного вала, чтобы не было пропусков или наложений частот.
26

27.

φ = 1,41
φ = 1,41
i1(1)
i2(1)
i1(2) i1(3)
i2(2)
iдоп= i0= 1000 / 750
(клиноременная передача от
эл. двигателя {nэл.дв=1000} к
входному валу коробки
скоростей {nвх.вала=750} ).
i1(1) = 750/355; i1(2) = 750/500;
i1(3) = 750/750;
i2(1) = 355/90; i2(2) = 355/250;
Рис. 4 а. Построение графика чисел оборотов выходного вала и промежуточных валов
График чисел оборотов выходного вала показывает все частоты вращения n при любых
комбинациях включенных передач и передаточные отношения i всех передач.
Для построения графика находим минимальное передаточное отношение коробки.
Общее минимальное передаточное отношение равно минимальной частоте вращения
выходного вала к частоте вращения двигателя, т.е. i0 = nmin(ni)/nдвигателя. Это
передаточное отношение равномерно распределяется на минимальные передаточные
отношения групп: imin = i01/m .
С целью ограничения радиальных размеров для зубчатых передач главного движения
передаточное отношение группы должно находиться в пределах 1/4 < i < 2. (Для прямозубых
передач imin> 1/4, imax< 2. Для косозубых imin > 1/4, imax< 2,5. Для механизмов подачи imin>1/5,
imax< 2,8. Для гитар сменных колес допускают imax < 4.) Передаточные отношения i,
выраженные через φр, приближенно могут быть представлены в виде простых дробей (т.к.
количество зубьев должно быть целое число): при φ=1,26: 1/1,26 = 4/5; 1/1,262 = 7/11; 1/1,263=
=1/2; 1/1,264 = 2/5; 1/1,265= 19/60; 1/1,266= 1/4; при φ=1,41: 1/1,41 ≈ 5/7; 1/1,412 = 1/2;
1/1,413=19/53=16/45; 1/1,414 = 1/4.
27

28.

φ = 1,41
iдоп= i0= 1000 / 750
(клиноременная передача от
эл. двигателя {nэл.дв=1000} к
входному валу коробки
скоростей {nвх.вала=750} ).
i1(1)
i2(1)
i1(2) i1(3)
i2(2)
i1(1) = 750/355; i1(2) = 750/500;
i1(3) = 750/750;
i2(1) = 355/90; i2(2) = 355/250;
Рис. 4 а. Построение графика чисел оборотов выходного вала и промежуточных валов
Передаточные отношения , выраженные через φр, приближенно могут быть представлены в виде простых дробей
(т.к. количество зубьев должно быть целое число): φ = 1,26 : 1/1,26 = 4/5; 1/1,262 = 7/11; 1/1,263=1/2; 1/1,264 = 2/5;
1/1,265= 19/60; 1/1,266= 1/4; φ = 1,41: 1/1,41 ≈ 5/7; 1/1,412 = 1/2; 1/1,413=19/53=16/45; 1/1,414 = 1/4. φ = 1,58; 1/1,58 =
7/11; 1/1,582 ~ 2/5; 1/1,583= 1/4.
Из этих данных видно, что передаточные отношения, не выходящие за пределы imin=1/4,
возможны в том случае, если линии, изображающие передачи, снижаются на графике
частот вращения не более чем на шесть интервалов для φ = 1,26, на четыре интервала
для φ = 1,41 (на рис. 4 для i2(1) – на 4 интервала), и на три интервала для φ = 1,58.
Если imin не удовлетворяет этому условию, то в коробку дополнительно вводят
дополнительную передачу с передаточным отношением iш, тогда передаточное отношение
коробки будет равно i0= iш /n, (i0 = nmin(ni)/nдвигателя).
Рекомендуется обеспечить такую последовательность передач в цепи, чтобы ij > i2>...im, т.е.
наибольшая редукция должна быть в конце цепи. Тогда крутящий момент, передаваемый
промежуточными передачами, будет меньше. Поэтому потребуются валы меньшего диаметра,
меньшие модули колес, т.е. конструкция коробки скоростей будет компактна.
28

29.

iдоп= i0= 1000 / 750
(клиноременная передача от
эл. двигателя {nэл.дв=1000} к
входному валу коробки
скоростей {nвх.вала=750} ).
φ = 1,41
i1(1) = 750/355; i1(2) = 750/500
i1(3) = 750/750;
i2(1) = 355/90; i2(2) = 355/250;
Рис. 4 б. Построение графика чисел оборотов выходного вала и промежуточных валов
Передаточные отношения: при φ = 1,26 : 1/1,26 = 4/5; 1/1,262 = 7/11; 1/1,263= =1/2; 1/1,264 = 2/5; 1/1,265= 19/60;
1/1,266= 1/4; при φ = 1,41: 1/1,41 ≈ 5/7; 1/1,412 = 1/2; 1/1,413=19/53=16/45; 1/1,414 = 1/4. при φ = 1,58; 1/1,58 = 7/11;
1/1,582 ~ 2/5; 1/1,583= 1/4.
Перед построением чисел оборотов строим сетку аналогично построению структурной сетки,
только добавляем еще один вал электродвигателя (нулевой - 0). Построение графика начинается
с группы с меньшим передаточным отношением (i = 1/4). Передаточное отношение первой
передачи iI-II = i12=ω1/ω2=n1/n2 =z2/z1=20/80=1/4. При модуле m=2мм делительный диаметр
меньшего зубчатого колеса (шестерни) d=m×z=2×20=40 мм, а диаметр вала должен быть меньше
него на величину ∆: ∆=2,5мм+20мм =22,5 мм, т.е. dвала<40- ∆= 40- 22,5=17,5 мм. Диаметр вала
слишком мал, недостаточна его жёсткость, поэтому при число зубьев должно быть больше 22,
или увеличить модуль m, или делать вал-шестерню.
С третьего вала (вал №3) с точки n1 = 90 об/мин проводим луч ко второму валу, отложив отрезок
равный 4φ, т.к. i2(1)=1/4, получаем точку на втором валу против n2 = 355 об/мин. Затем от этой точки
проводим луч к первому валу, отложив от нее отрезок 2φ, т.к. отношение i1(1)=1/2 для φ = 1,41 равно
2 (получим точку на первом валу против n1 = 750 об/мин). Так как во второй группе две передачи, их
необходимо отразить двумя лучами, расстояние между ними равно 3φ, т.е. расстояние от первого
луча до второго равно 3φ.
29

30.

iдоп= i0= 1000 / 750
(клиноременная передача от
эл. двигателя {nэл.дв=1000} к
входному валу коробки
скоростей {nвх.вала=750} ).
i1(1) = 750/355; i1(2) = 750/500
i1(3) = 750/750;
i2(1) = 355/90; i2(2) = 355/250;
Рис. 4 б. Построение графика чисел оборотов выходного вала и промежуточных валов
Передаточные отношения: φ = 1,26 : 1/1,26 = 4/5; 1/1,262 = 7/11; 1/1,263= =1/2; 1/1,264 = 2/5; 1/1,265= 19/60; 1/1,266=
1/4; φ = 1,41: 1/1,41 ≈ 5/7; 1/1,412 = 1/2; 1/1,413=19/53=16/45; 1/1,414 = 1/4. При φ = 1,58; 1/1,58 = 7/11; 1/1,582 ~ 2/5;
1/1,583= 1/4.
По найденным передаточным отношениям определяют число зубьев зубчатых колес. В
группе передач сумма чисел зубьев зубчатых пар постоянна: Z1 + Z2 = Z3 +
Z4 =...=const. Число зубьев колес можно
представить в виде суммы зубьев Vz (z*).
Пример: Величины а и b определяются исходя из передаточных отношений со 2-го вала
на 3-й: i1= a/b = z1/z2; i2= c/d = z3/z4. Сумма количества зубьев: z*=Vz=z1+z2 = z3+z4 . Для
определения числа зубьев находят наименьшее общее кратное сумм a+b+c+d и
подставляют его вместо Vz.
Исходя из компактности передач величину Vz ограничивают в пределах 100…120.
Минимальное число зубьев в приводах главного движения z=18...20, в механизмах подач
- z=16.
30

31.

iдоп= i0= 1000 / 750
(клиноременная передача от
эл. двигателя {nэл.дв=1000} к
входному валу коробки
скоростей {nвх.вала=750} ).
i1(1) = 750/355; i1(2) = 750/500
i1(3) = 750/750;
i2(1) = 355/90; i2(2) = 355/250;
Рис. 4 б. Построение графика чисел оборотов выходного вала и промежуточных валов
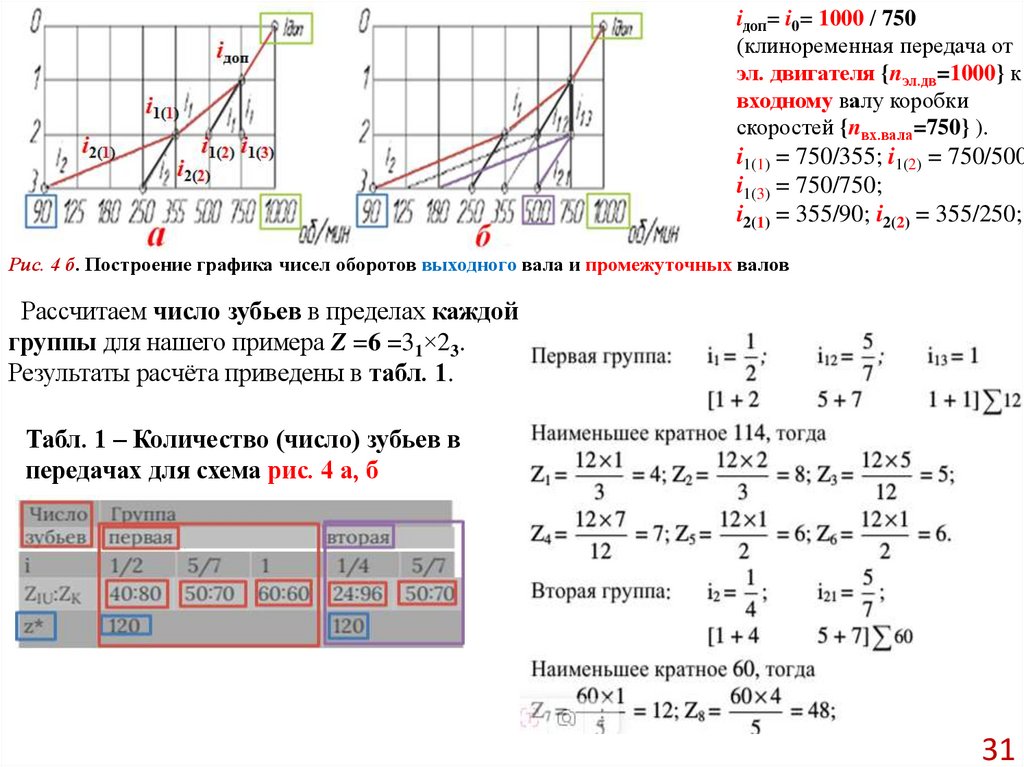
Рассчитаем число зубьев в пределах каждой
группы для нашего примера Z =6 =31×23.
Результаты расчёта приведены в табл. 1.
Табл. 1 – Количество (число) зубьев в
передачах для схема рис. 4 а, б
31

32. 4.4 Передаточные механизмы (продолжение 64)

Планетарная передача (ПП) — механическая передача
вращательного движения, за счёт своей конструкции
способная в пределах одной геометрической оси вращения
изменять, складывать и раскладывать подводимые угловые
скорости и/или крутящий момент. Обычно является
элементом трансмиссии различных технологических и
транспортных машин. Конструктивно ПП всегда
представляет собой набор взаимозацепленных зубчатых
колёс (не менее 4), часть из которых (не менее 2) имеет
общую геометрическую неподвижную ось вращения, а
другая часть (также, не менее 2) имеет подвижные оси
вращения, концентрически вращающиеся на так
Рис. 5. Планетарная передача
называемом «водиле» вокруг неподвижной.
Зубчатые колёса на неподвижной оси всегда связаны друг с другом не напрямую, а через
зубчатые колёса на подвижных осях, а ввиду того, что вторые способны не только вращаться
относительно первых, но и обкатывать их, тем самым передавая поступательное движение на
водило, все звенья ПП, на которые можно подавать/снимать мощность, получают возможность
вращаться дифференциально, с тем лишь условием, что угловая скорость любого такого звена не
абсолютно хаотична, а определяется угловыми скоростями всех остальных звеньев. В этом
плане ПП похожа на планетарную систему, в которой скорость каждой планеты определяется
скоростями всех остальных планет системы. Дифференциальный принцип вращения всей
системы, а также то, что в своём каноническом виде набор зубчатых колёс, составляющих ПП,
собран в некоем подобии солнца и эпициклически движущихся по орбите планет, даёт данной
механической передаче такие присущие только ей интернациональные определения, как
планетарная, дифференциальная (от лат. differentia — разность, различие) или эпициклическая,
каждое из которых в данном случае есть синонимы.
32

33. 4.4 Передаточные механизмы (продолжение 65)

С точки зрения теоретической механики планетарная
передача — это механическая система с двумя и
более степенями свободы. Эта особенность,
являющаяся прямым следствием конструкции, есть
важное отличие ПП от каких-либо других передач
вращательного движения, всегда имеющих только
одну степень свободы. И эта особенность наделяет
саму ПП тем важным качеством, что в аспекте
воздействия на угловые скорости вращения ПП может
не только редуцировать эти скорости, но и
складывать и раскладывать их, что, в свою очередь,
делает её основным механическим исполнительным
узлом не только различных планетарных редукторов,
но и таких устройств, как дифференциалы и
суммирующие ПП.
б
а
в
е
г
д
Рис. 6. Планетарные передачи
33

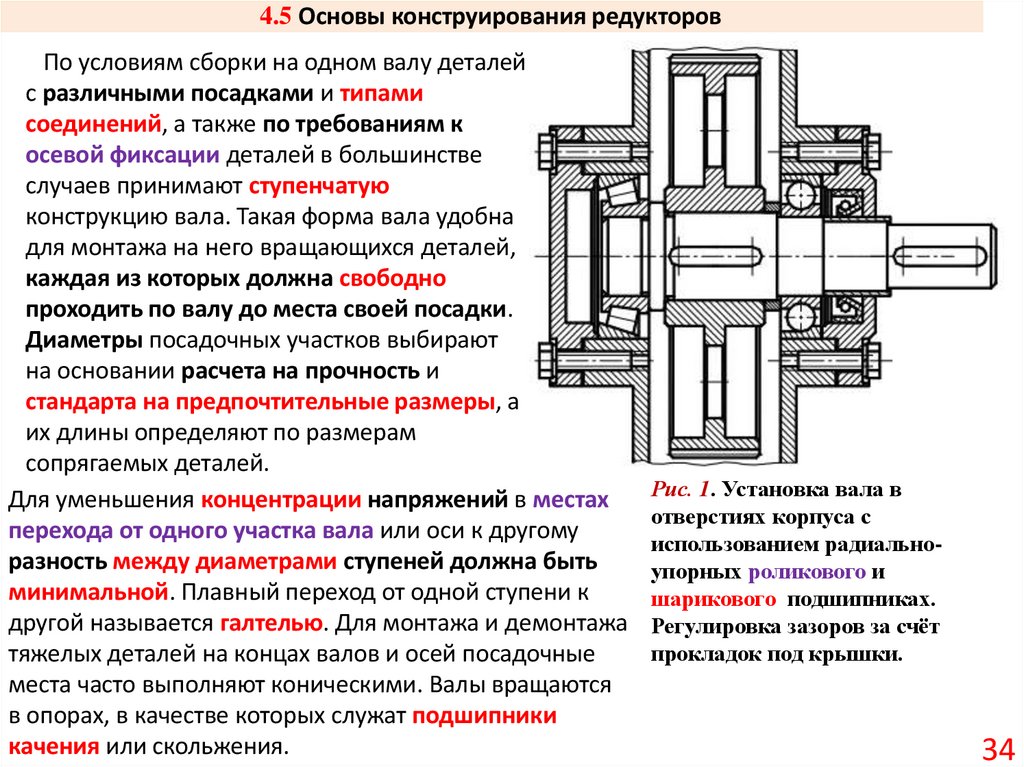
34. 4.5 Основы конструирования редукторов

По условиям сборки на одном валу деталей
с различными посадками и типами
соединений, а также по требованиям к
осевой фиксации деталей в большинстве
случаев принимают ступенчатую
конструкцию вала. Такая форма вала удобна
для монтажа на него вращающихся деталей,
каждая из которых должна свободно
проходить по валу до места своей посадки.
Диаметры посадочных участков выбирают
на основании расчета на прочность и
стандарта на предпочтительные размеры, а
их длины определяют по размерам
сопрягаемых деталей.
Для уменьшения концентрации напряжений в местах
перехода от одного участка вала или оси к другому
разность между диаметрами ступеней должна быть
минимальной. Плавный переход от одной ступени к
другой называется галтелью. Для монтажа и демонтажа
тяжелых деталей на концах валов и осей посадочные
места часто выполняют коническими. Валы вращаются
в опорах, в качестве которых служат подшипники
качения или скольжения.
Рис. 1. Установка вала в
отверстиях корпуса с
использованием радиальноупорных роликового и
шарикового подшипниках.
Регулировка зазоров за счёт
прокладок под крышки.
34

35. 4.5 Основы конструирования редукторов (продолжение 1)

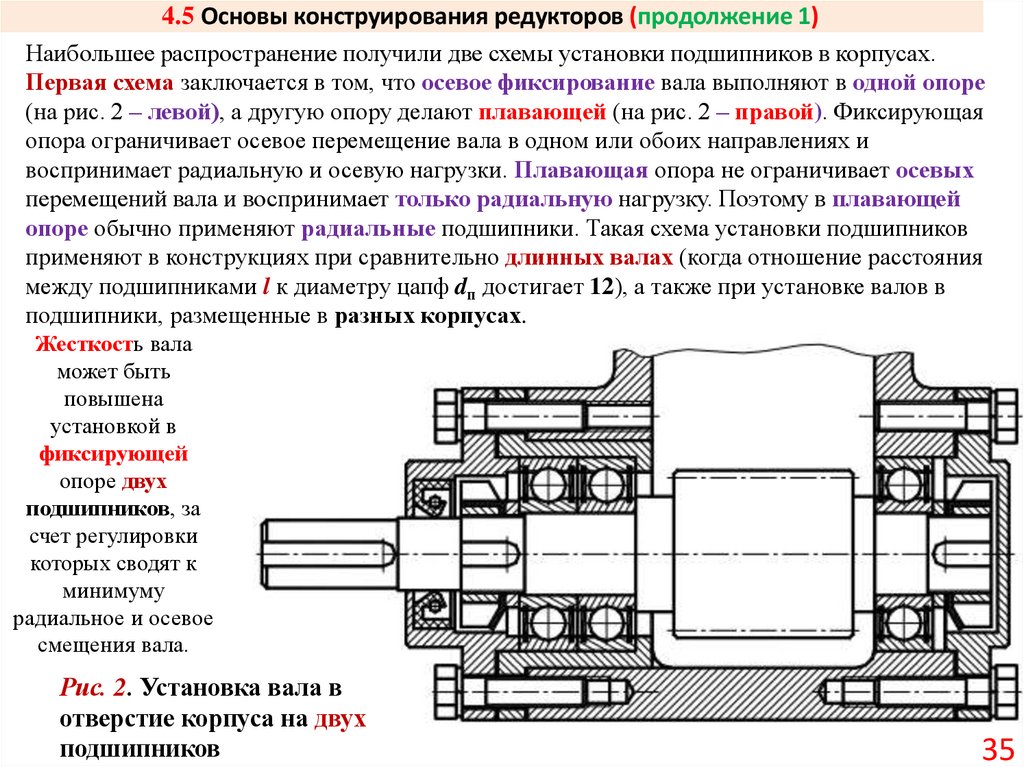
Наибольшее распространение получили две схемы установки подшипников в корпусах.
Первая схема заключается в том, что осевое фиксирование вала выполняют в одной опоре
(на рис. 2 – левой), а другую опору делают плавающей (на рис. 2 – правой). Фиксирующая
опора ограничивает осевое перемещение вала в одном или обоих направлениях и
воспринимает радиальную и осевую нагрузки. Плавающая опора не ограничивает осевых
перемещений вала и воспринимает только радиальную нагрузку. Поэтому в плавающей
опоре обычно применяют радиальные подшипники. Такая схема установки подшипников
применяют в конструкциях при сравнительно длинных валах (когда отношение расстояния
между подшипниками l к диаметру цапф dп достигает 12), а также при установке валов в
подшипники, размещенные в разных корпусах.
Жесткость вала
может быть
повышена
установкой в
фиксирующей
опоре двух
подшипников, за
счет регулировки
которых сводят к
минимуму
радиальное и осевое
смещения вала.
Рис. 2. Установка вала в
отверстие корпуса на двух
подшипников
35

36. 4.5 Основы конструирования редукторов (продолжение 2)

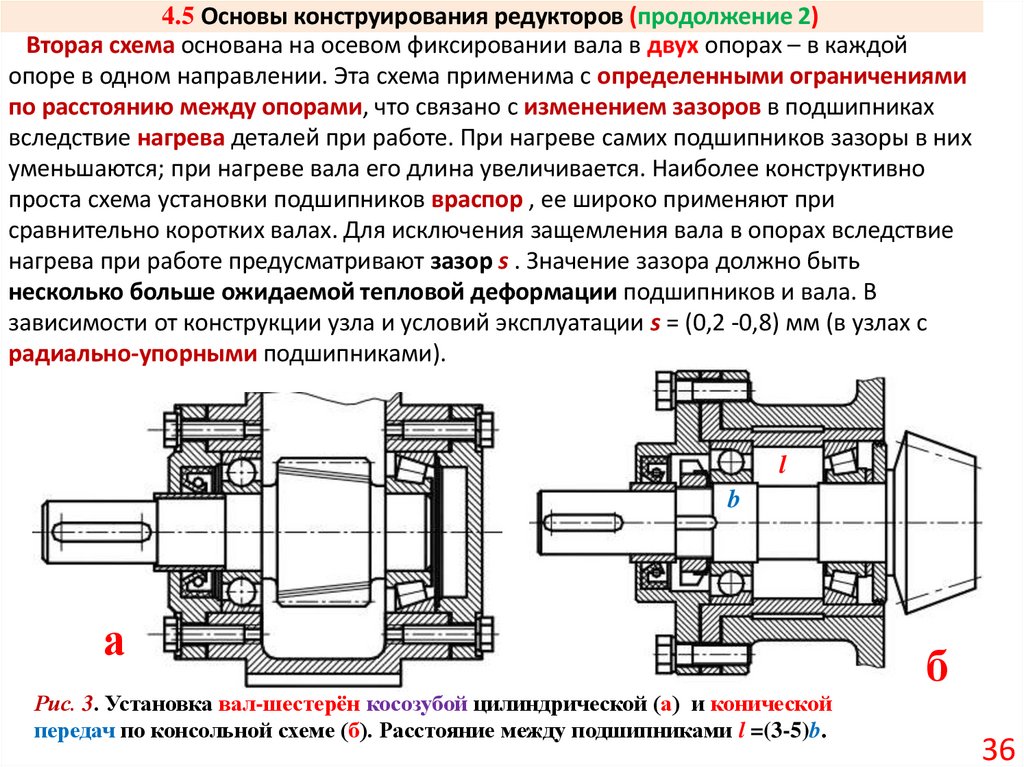
Вторая схема основана на осевом фиксировании вала в двух опорах – в каждой
опоре в одном направлении. Эта схема применима с определенными ограничениями
по расстоянию между опорами, что связано с изменением зазоров в подшипниках
вследствие нагрева деталей при работе. При нагреве самих подшипников зазоры в них
уменьшаются; при нагреве вала его длина увеличивается. Наиболее конструктивно
проста схема установки подшипников враспор , ее широко применяют при
сравнительно коротких валах. Для исключения защемления вала в опорах вследствие
нагрева при работе предусматривают зазор s . Значение зазора должно быть
несколько больше ожидаемой тепловой деформации подшипников и вала. В
зависимости от конструкции узла и условий эксплуатации s = (0,2 -0,8) мм (в узлах с
радиально-упорными подшипниками).
l
b
а
Рис. 3. Установка вал-шестерён косозубой цилиндрической (а) и конической
передач по консольной схеме (б). Расстояние между подшипниками l =(3-5)b.
б
36

37. 4.5 Основы конструирования редукторов (продолжение 3)

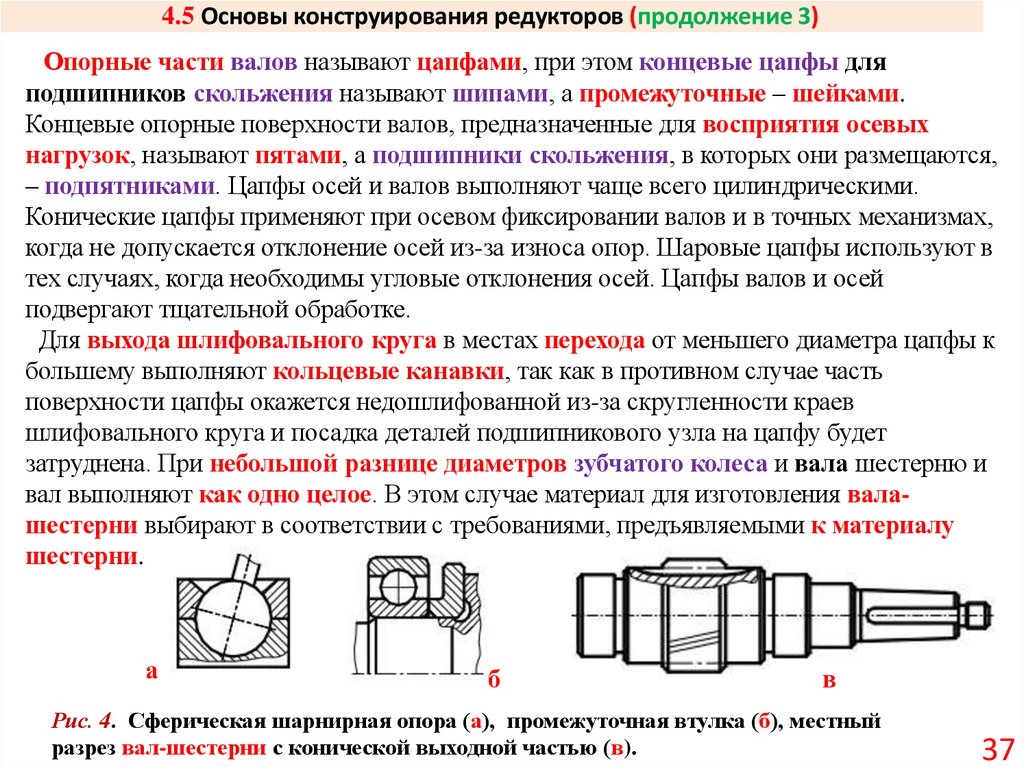
Опорные части валов называют цапфами, при этом концевые цапфы для
подшипников скольжения называют шипами, а промежуточные – шейками.
Концевые опорные поверхности валов, предназначенные для восприятия осевых
нагрузок, называют пятами, а подшипники скольжения, в которых они размещаются,
– подпятниками. Цапфы осей и валов выполняют чаще всего цилиндрическими.
Конические цапфы применяют при осевом фиксировании валов и в точных механизмах,
когда не допускается отклонение осей из-за износа опор. Шаровые цапфы используют в
тех случаях, когда необходимы угловые отклонения осей. Цапфы валов и осей
подвергают тщательной обработке.
Для выхода шлифовального круга в местах перехода от меньшего диаметра цапфы к
большему выполняют кольцевые канавки, так как в противном случае часть
поверхности цапфы окажется недошлифованной из-за скругленности краев
шлифовального круга и посадка деталей подшипникового узла на цапфу будет
затруднена. При небольшой разнице диаметров зубчатого колеса и вала шестерню и
вал выполняют как одно целое. В этом случае материал для изготовления валашестерни выбирают в соответствии с требованиями, предъявляемыми к материалу
шестерни.
а
б
в
Рис. 4. Сферическая шарнирная опора (а), промежуточная втулка (б), местный
разрез вал-шестерни с конической выходной частью (в).
37

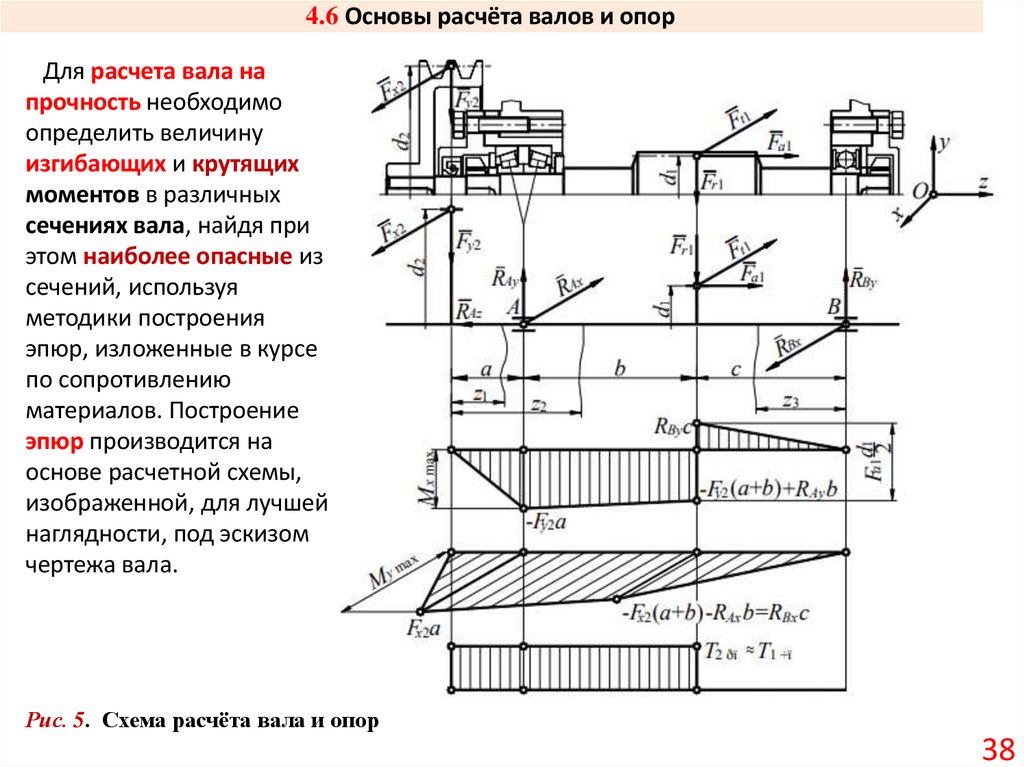
38. 4.6 Основы расчёта валов и опор

Для расчета вала на
прочность необходимо
определить величину
изгибающих и крутящих
моментов в различных
сечениях вала, найдя при
этом наиболее опасные из
сечений, используя
методики построения
эпюр, изложенные в курсе
по сопротивлению
материалов. Построение
эпюр производится на
основе расчетной схемы,
изображенной, для лучшей
наглядности, под эскизом
чертежа вала.
Рис. 5. Схема расчёта вала и опор
38