Similar presentations:
6-Поверхности
1. НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Лекция 6. ПОВЕРХНОСТИ. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙАвтор презентации:
доцент кафедры «Инженерная графика»
Тамара Владимировна Нестерова
2. Поверхности
2Способы задания поверхностей
Классификация
Способы задания
Многогранники
Поверхности вращения
3. Способы задания поверхностей
АналитическийГрафический
Каркасом, слайд 4
Очерком, слайд 5
Проекциями образующей и направляющей
Проекцией образующей и осью – для поверхности
вращения, слайд 6
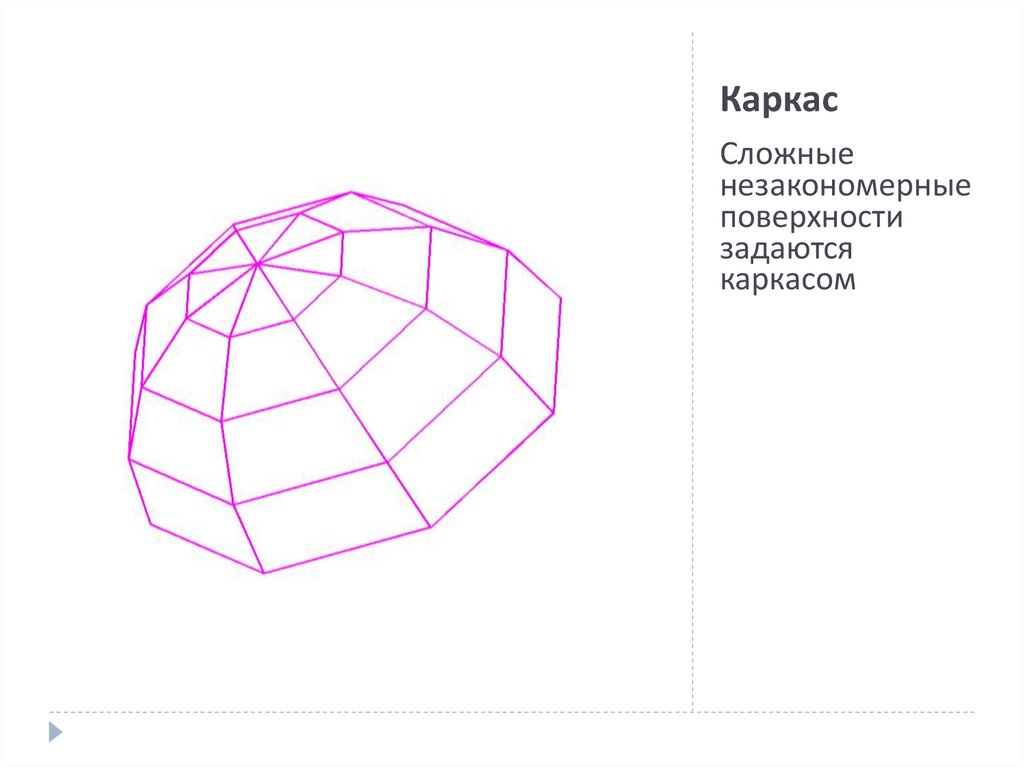
4. Каркас
Сложныенезакономерные
поверхности
задаются
каркасом
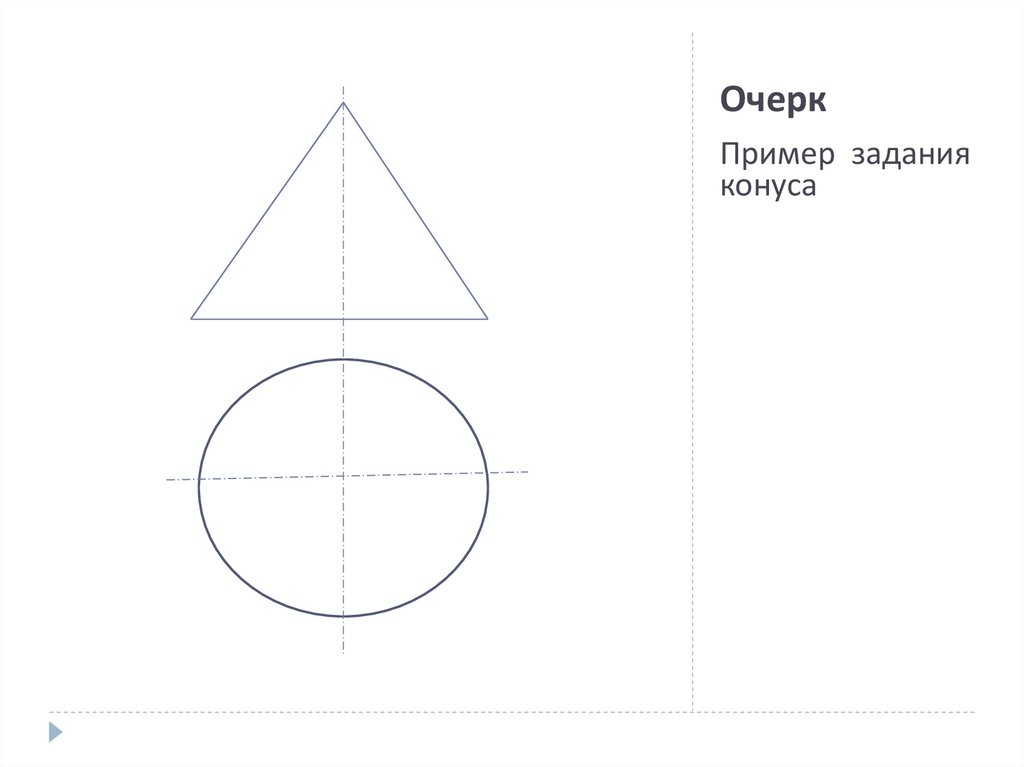
5. Очерк
Пример заданияконуса
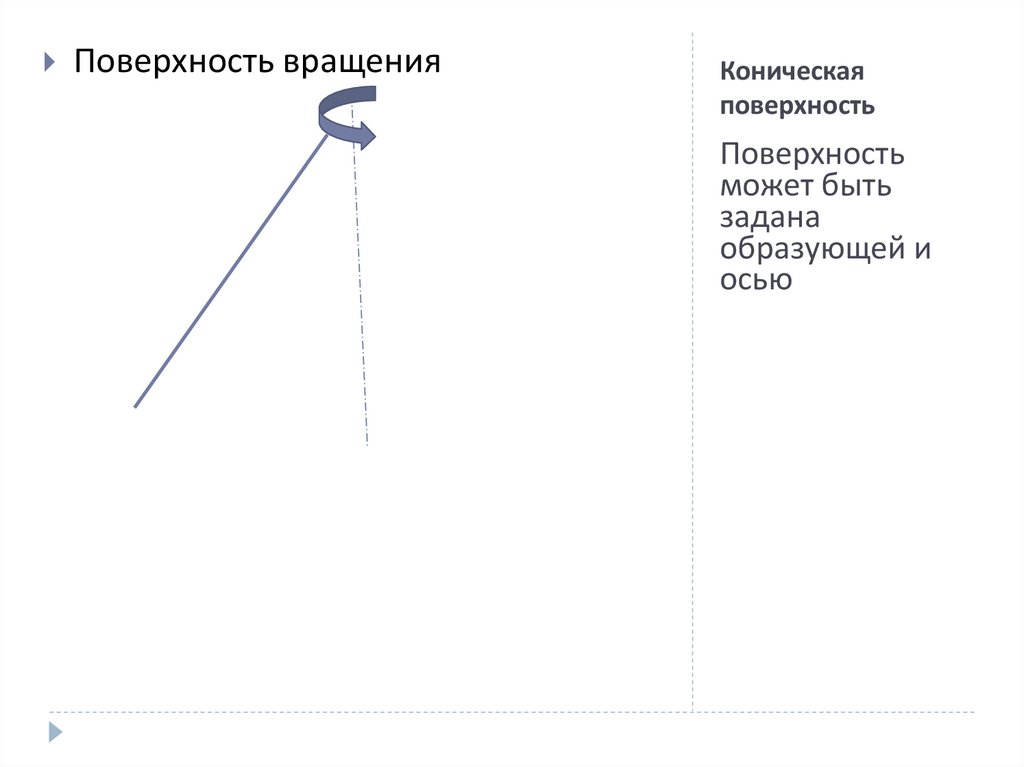
6. Коническая поверхность
Поверхность вращенияКоническая
поверхность
Поверхность
может быть
задана
образующей и
осью
7. Линейчатые поверхности
Это поверхности полученные при поступательномдвижении прямой линии (образующей):
цилиндрические
конические
поверхности с ребром возврата
7
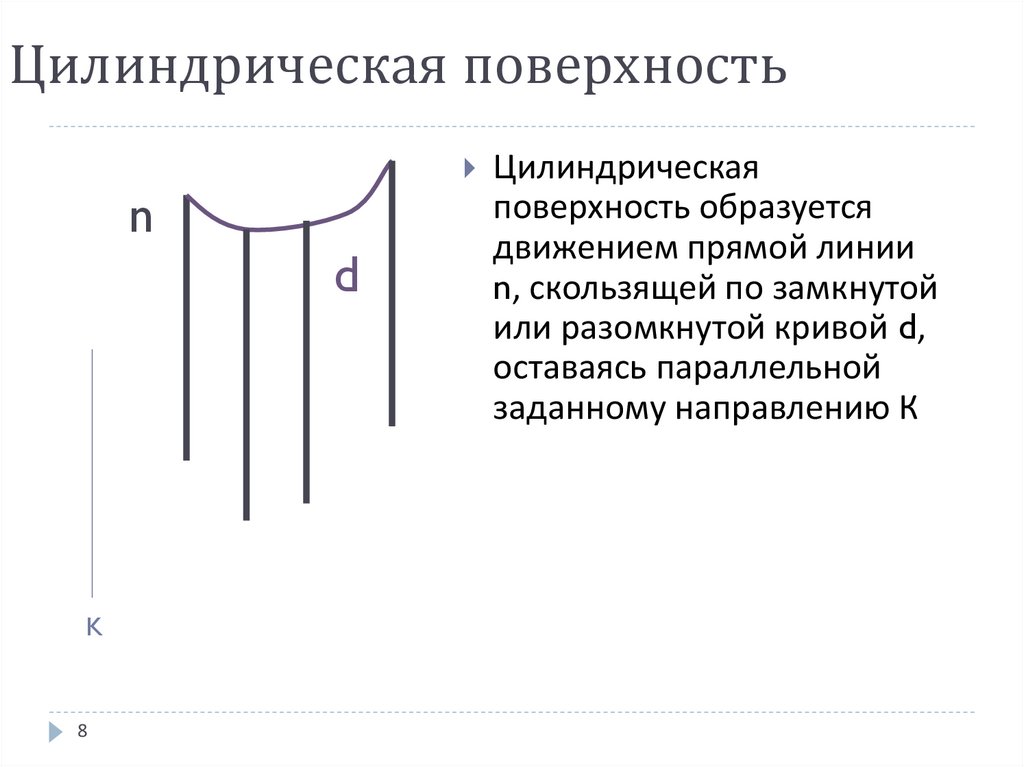
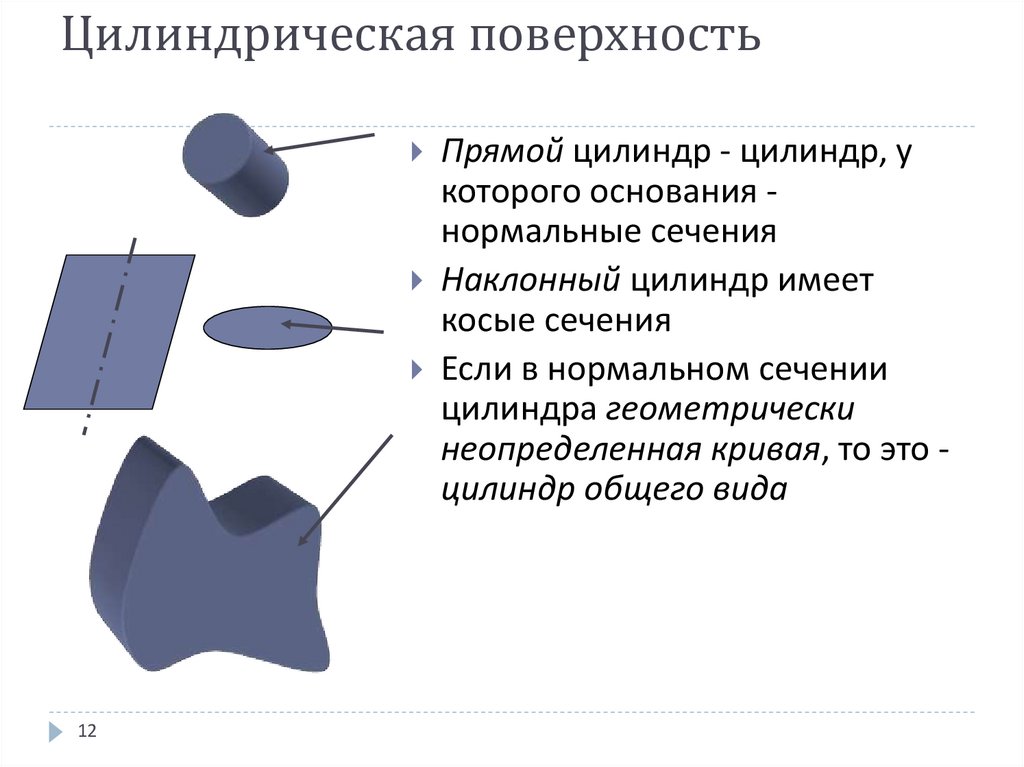
8. Цилиндрическая поверхность
Цилиндрическаяn
d
K
8
поверхность образуется
движением прямой линии
n, скользящей по замкнутой
или разомкнутой кривой d,
оставаясь параллельной
заданному направлению К
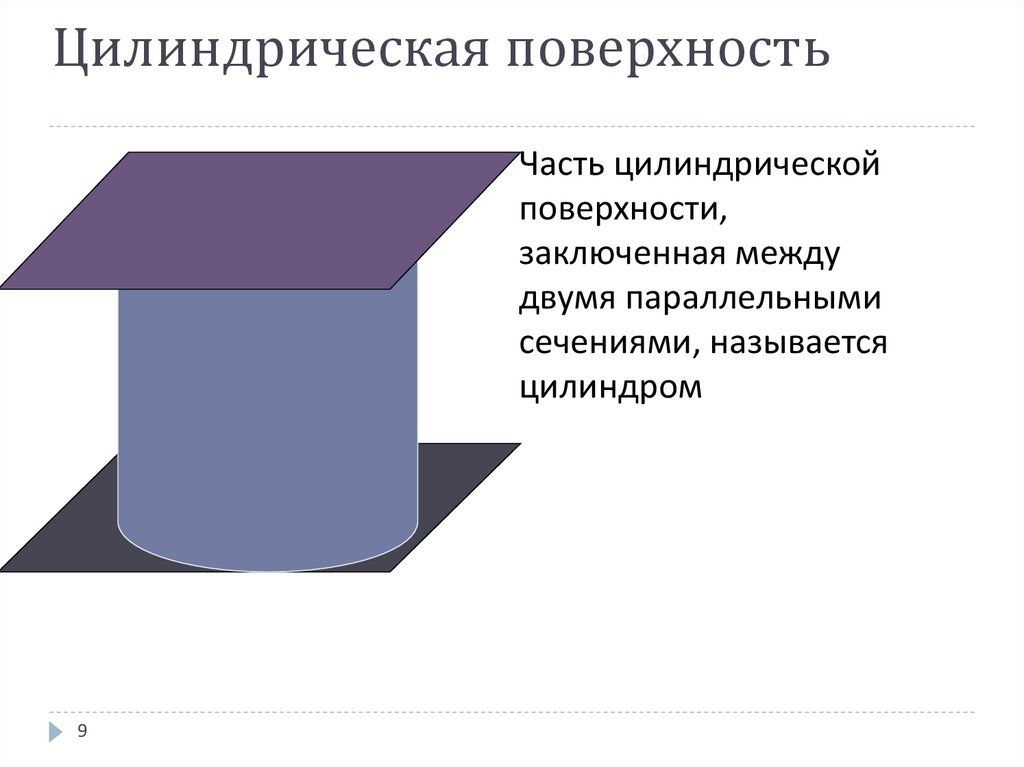
9. Цилиндрическая поверхность
Часть цилиндрическойповерхности,
заключенная между
двумя параллельными
сечениями, называется
цилиндром
9
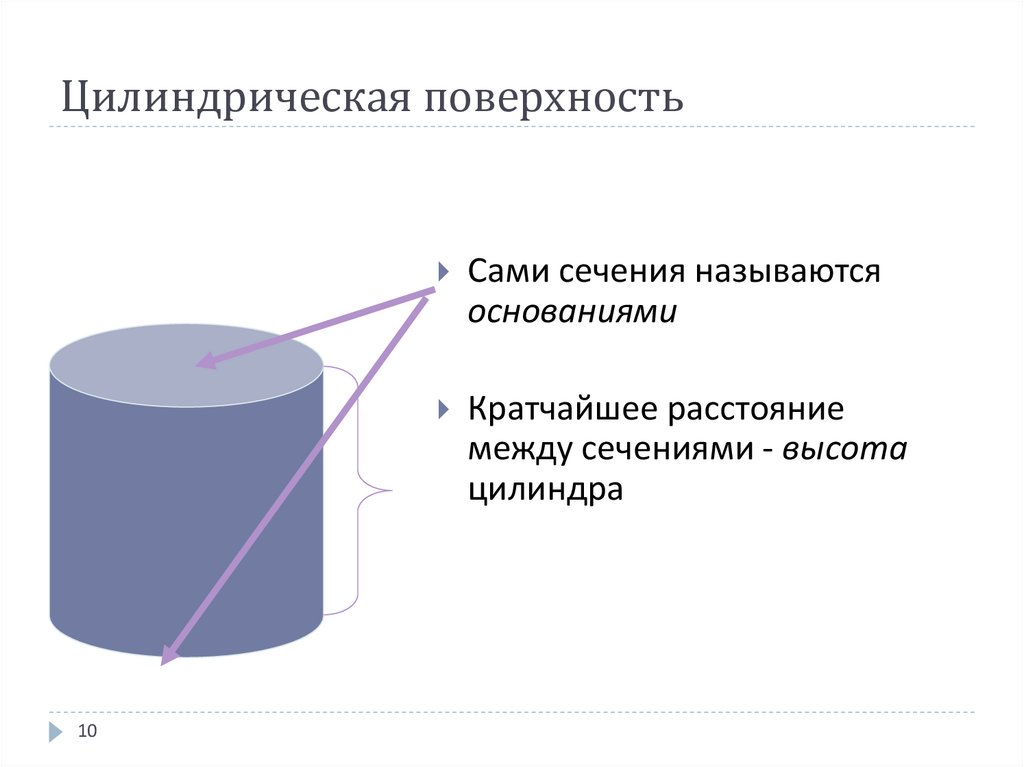
10. Цилиндрическая поверхность
Сами сечения называютсяоснованиями
Кратчайшее расстояние
между сечениями - высота
цилиндра
10
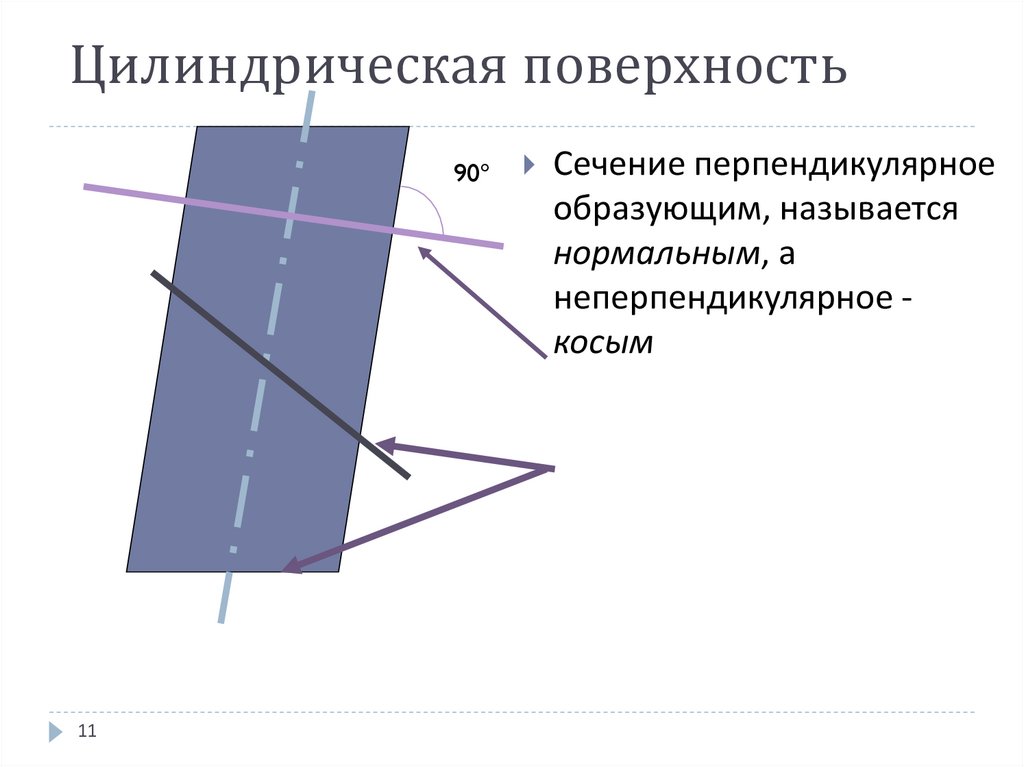
11. Цилиндрическая поверхность
90°Сечение перпендикулярное
образующим, называется
нормальным, а
неперпендикулярное косым
11
12. Цилиндрическая поверхность
Прямой цилиндр - цилиндр, укоторого основания нормальные сечения
Наклонный цилиндр имеет
косые сечения
Если в нормальном сечении
цилиндра геометрически
неопределенная кривая, то это цилиндр общего вида
12
13. Цилиндрическая поверхность
По виду нормального сечения цилиндры делятсяна:
круговые
эллиптические
параболические
циклоидальные и т.п.
Цилиндры гиперболический, параболический,
циклоидальный - цилиндры открытого типа
13
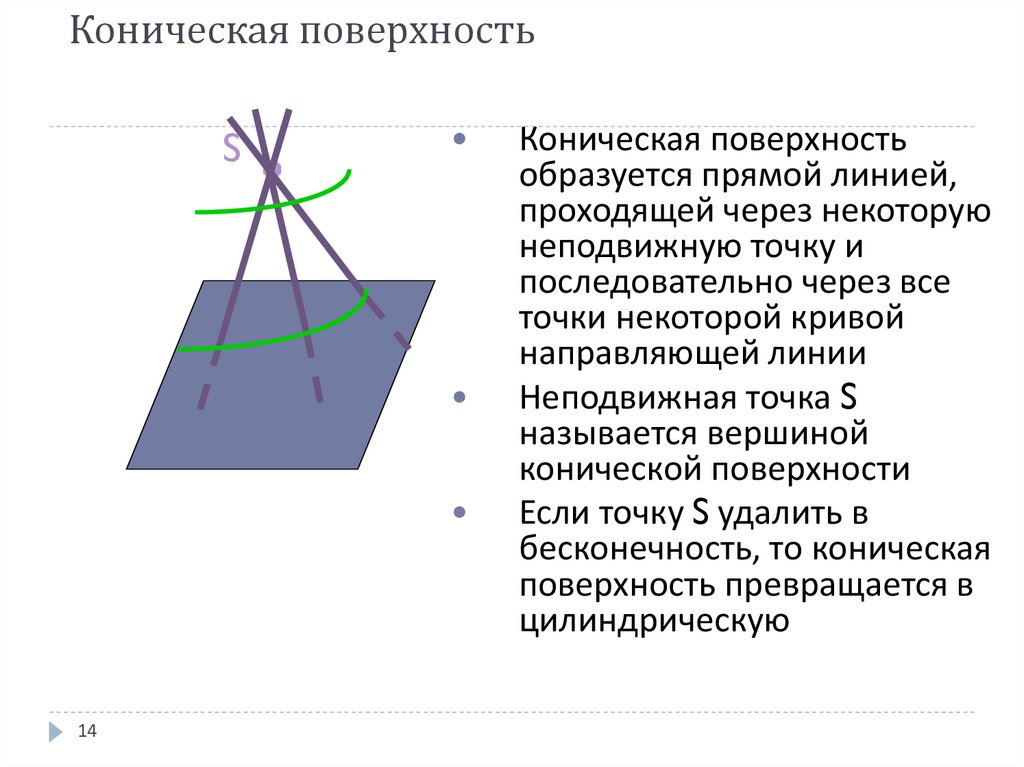
14. Коническая поверхность
S14
Коническая поверхность
образуется прямой линией,
проходящей через некоторую
неподвижную точку и
последовательно через все
точки некоторой кривой
направляющей линии
Неподвижная точка S
называется вершиной
конической поверхности
Если точку S удалить в
бесконечность, то коническая
поверхность превращается в
цилиндрическую
15. ВЫВОДЫ
1.2.
3.
15
Задать поверхность на чертеже – значит
указать условия, позволяющие построить
каждую точку этой поверхности
Для задания поверхности достаточно иметь
проекции направляющей линии и указать
образующую линию
Цилиндрическая поверхность образуется
прямой линией, сохраняющей во всех
положениях параллельность некоторой
заданной прямой линии и проходящей
последовательно через все точки
направляющей линии
16. Винтовые поверхности -
Винтовые поверхности Это поверхности, получаемые при винтовомдвижении прямолинейной образующей
В зависимости от того, как расположена
образующая относительно оси винтовой линии,
различают винтовые поверхности:
прямую
косую
эвольвентную
конволютную
16
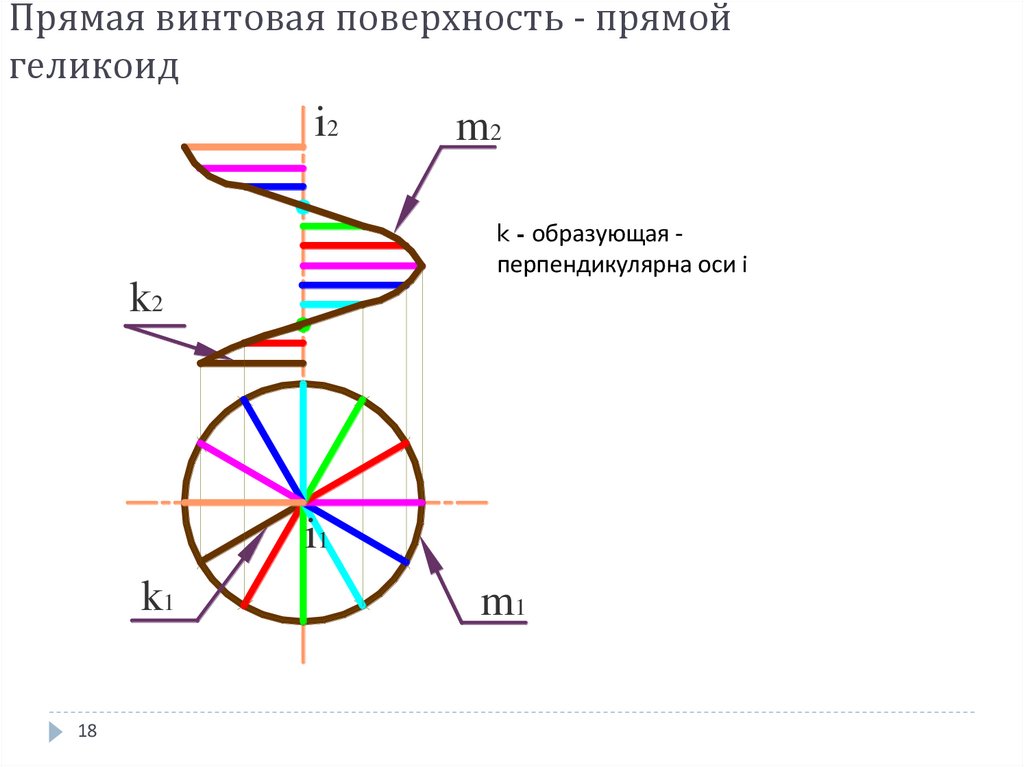
17. Винтовые поверхности
Прямая винтовая поверхность - прямойгеликоид - получается при винтовом движении
образующей, перпендикулярной прямой
направляющей (оси)
Наклонный (косой) геликоид - образующая
имеет постоянный угол, отличный от прямого
Эвольвентная винтовая поверхность
получается при движении образующей, которая во
всех своих положениях касается винтовой линии
17
18. Прямая винтовая поверхность - прямой геликоид
i22m2
k - образующая перпендикулярна оси i
k2
i1
i1
k1
18
m1
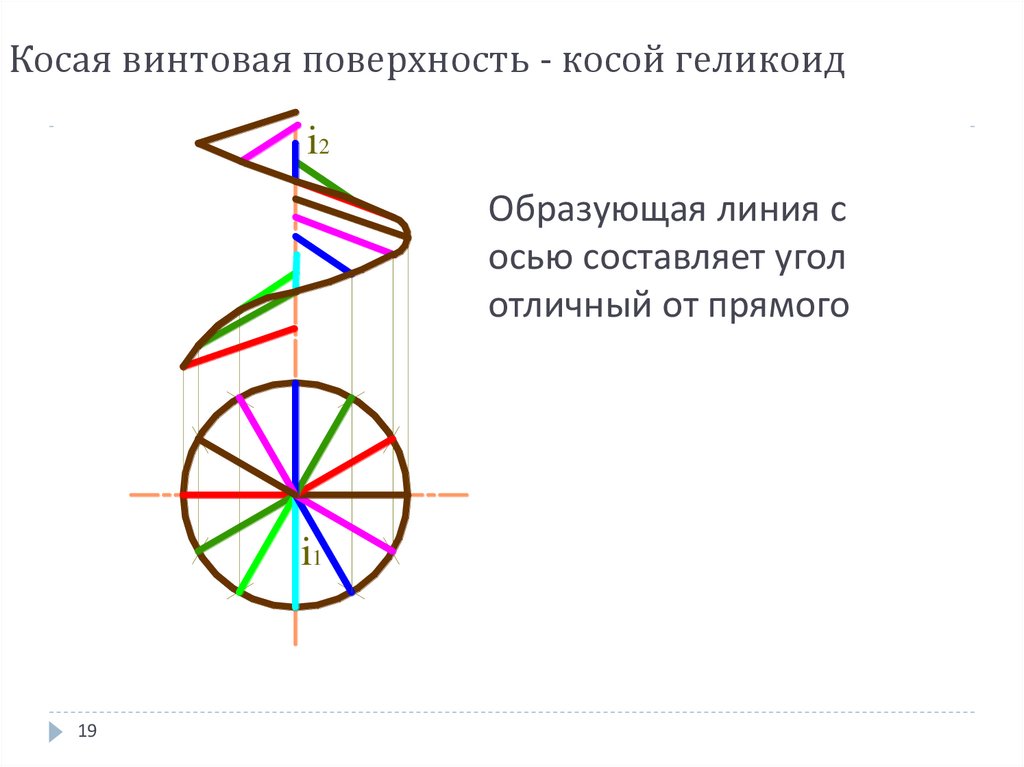
19. Косая винтовая поверхность - косой геликоид
i2Образующая линия с
осью составляет угол
отличный от прямого
i1
i1
19
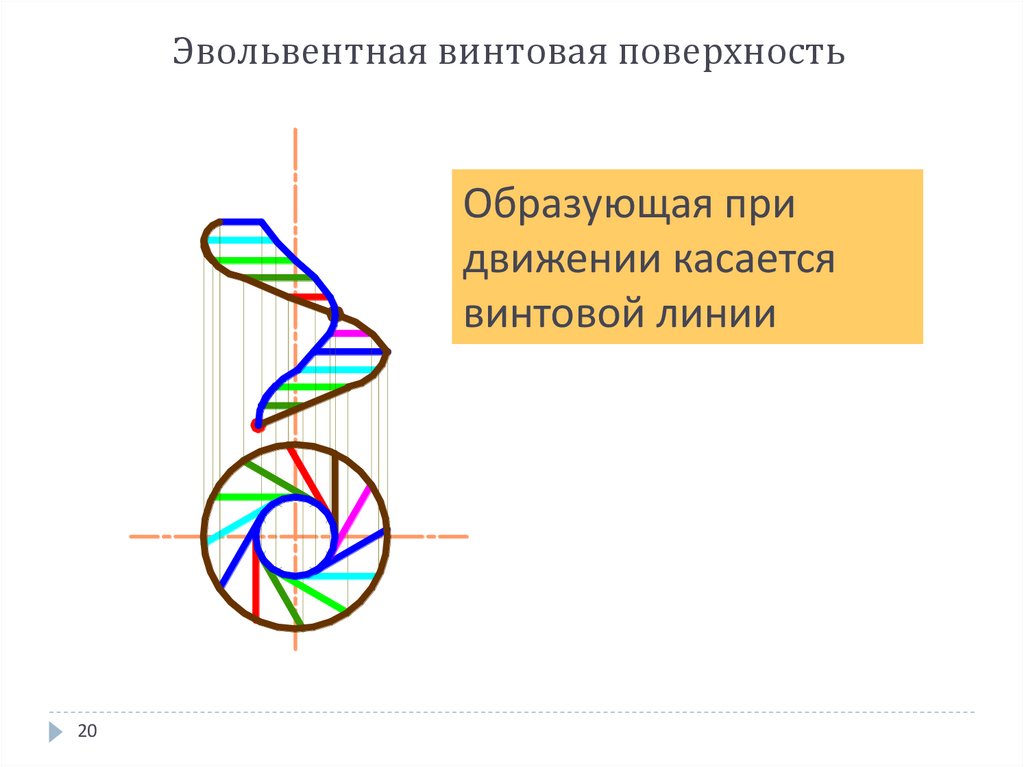
20. Эвольвентная винтовая поверхность
Образующая придвижении касается
винтовой линии
20
21. ВЫВОДЫ
Винтовая поверхность образуется винтовымперемещением производящей линии
Винтовое перемещение слагается из
вращательного и поступательного вдоль оси
Винтовые поверхности с производящими
прямыми линиями называют геликоидами
Геликоид называют прямым, если
производящая прямая линия составляет с осью
прямой угол
В других случаях геликоид называют
наклонным или косым
21
22. Контрольные вопросы
Какие винтовые поверхности называют геликоидами?Укажите их виды
22
23. Контрольные вопросы
1.2.
23
Укажите основные способы задания поверхностей
Что называют каркасом поверхности?
24. СЕЧЕНИЕ ПОВЕРХНОСТИ
При пересечении поверхности плоскостью получаетсялиния, все точки которой принадлежат поверхности и
секущей плоскости
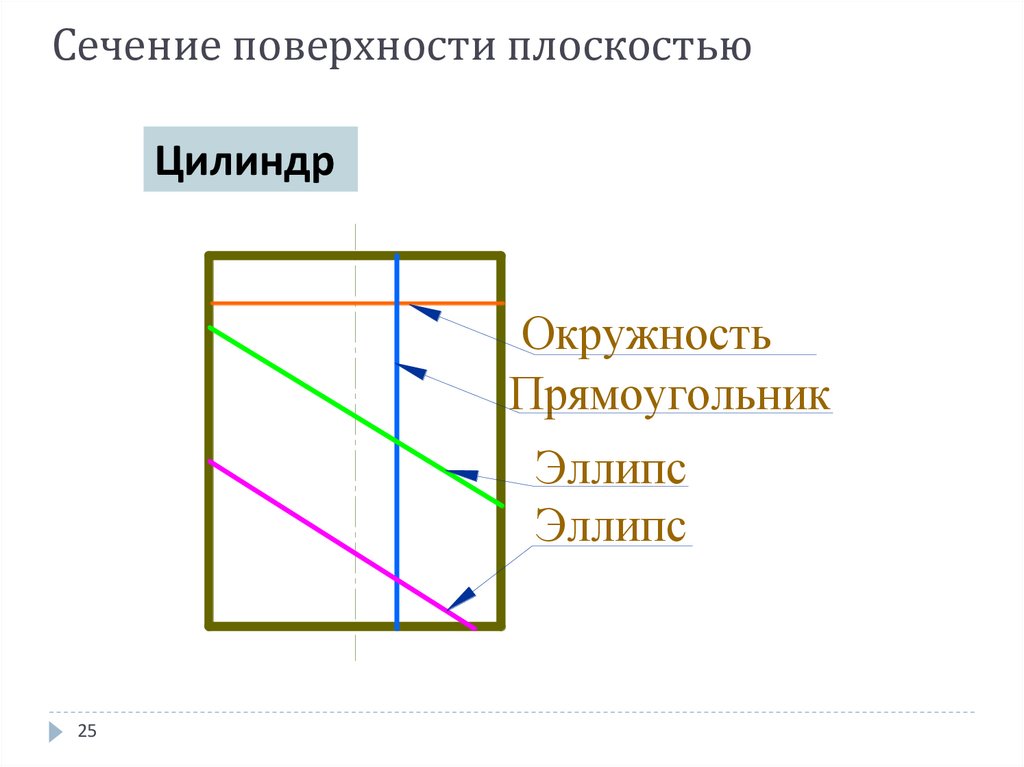
25. Сечение поверхности плоскостью
ЦилиндрОкружность
Прямоугольник
Эллипс
Эллипс
25
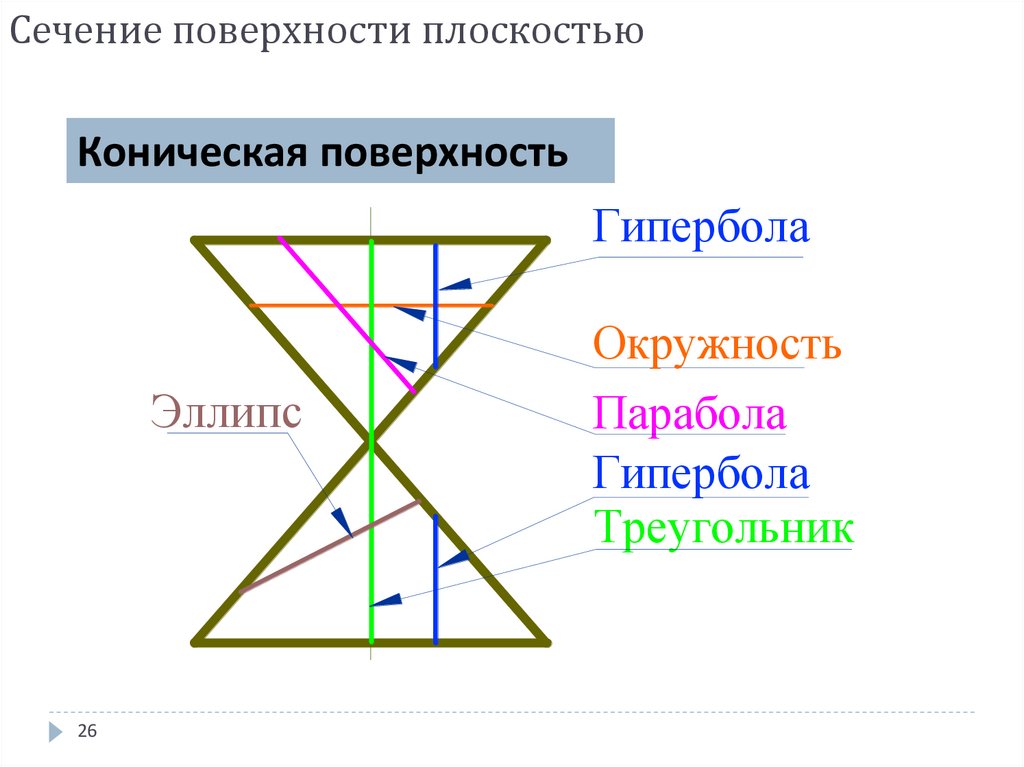
26. Сечение поверхности плоскостью
Коническая поверхностьГипербола
Эллипс
26
Окружность
Парабола
Гипербола
Треугольник
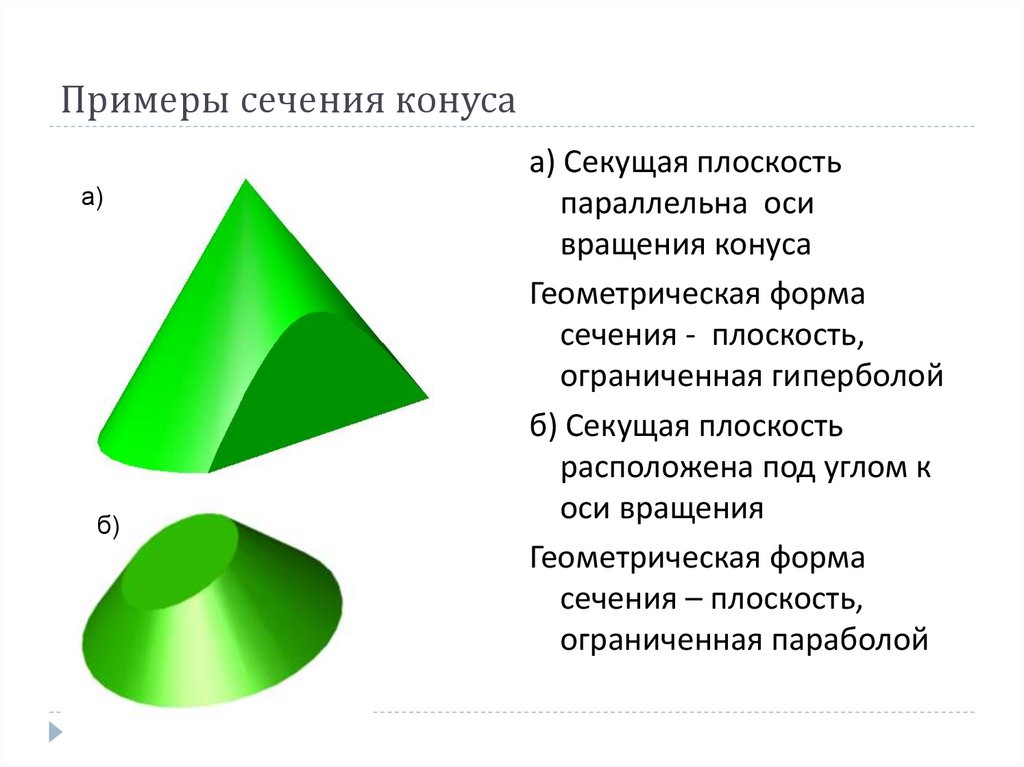
27. Примеры сечения конуса
а)б)
а) Секущая плоскость
параллельна оси
вращения конуса
Геометрическая форма
сечения - плоскость,
ограниченная гиперболой
б) Секущая плоскость
расположена под углом к
оси вращения
Геометрическая форма
сечения – плоскость,
ограниченная параболой
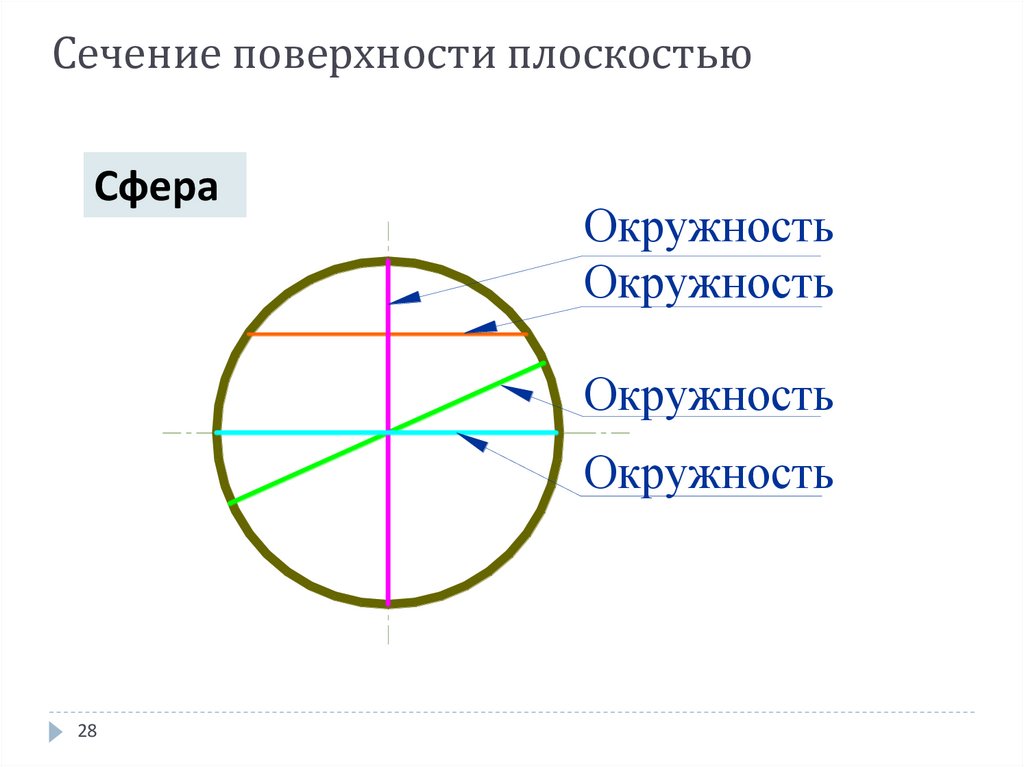
28. Сечение поверхности плоскостью
СфераОкружность
Окружность
Окружность
Окружность
28
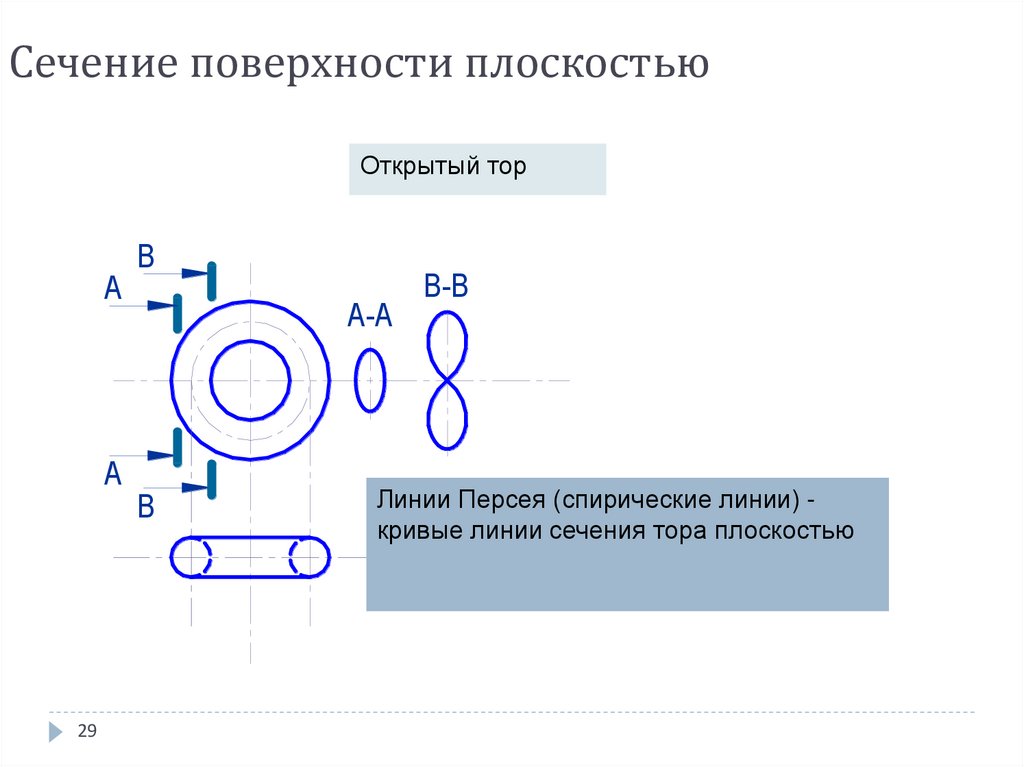
29. Сечение поверхности плоскостью
Открытый торA
A
29
B
A-A
B
B-B
Линии Персея (спирические линии) кривые линии сечения тора плоскостью
30. Сечение поверхностей плоскостью
Построение сечений1. Анализ заданной поверхности. Если секущая
плоскость - проецирующая, то одна проекция сечения
на чертеже совпадает с линией следа плоскости
2. Определение характерных точек, принадлежащих
линии пересечения:
2.1.Точки лежащие на крайних образующих
2.2. Точки определяющие границу видимости
2.3. Точки максимального и минимального удаления от
плоскостей проекций (вершины кривых линий)
30
31. Сечение поверхности плоскостью
Проведение вспомогательной секущей плоскостичастного положения – горизонтальной или
фронтальной
Выбор плоскости основан на получении в сечении
простых геометрических фигур – треугольников,
окружностей, прямоугольников
3.
4.
5.
31
Построение линий пересечения
вспомогательной плоскости с заданными
поверхностью и плоскостью
Определение точек пересечения построенных
линий
32. Сечение поверхности плоскостью
6.7.
32
Повторение пунктов 3, 4, 5 n раз
Соединение полученных точек с учетом видимости
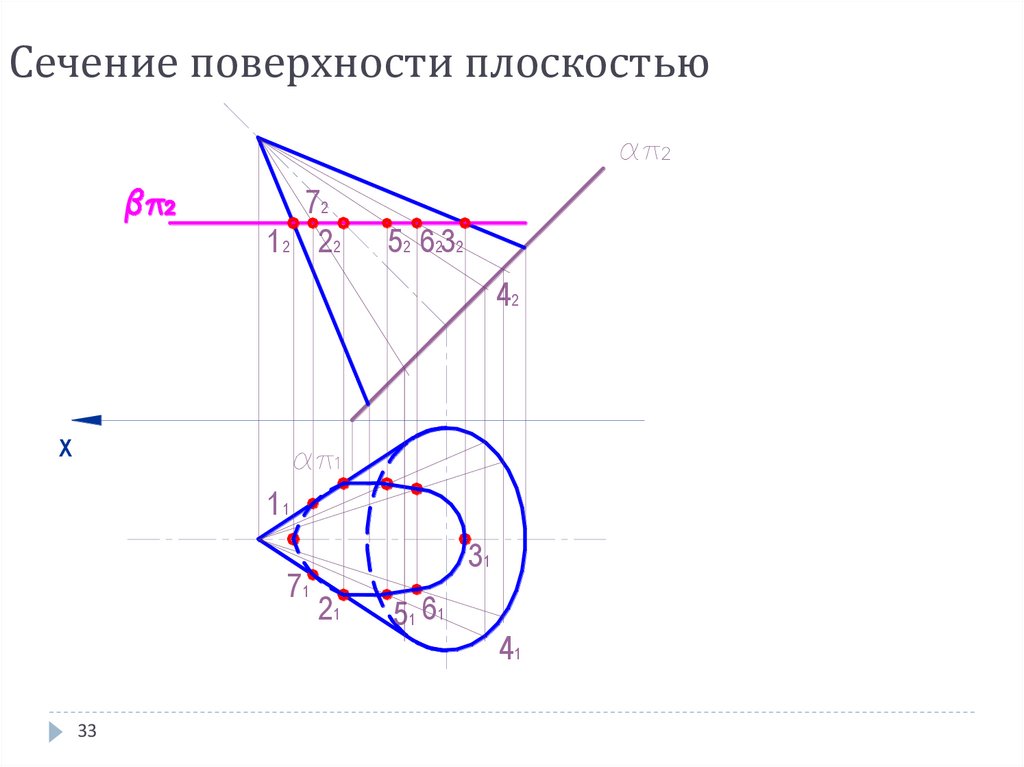
33. Сечение поверхности плоскостью
721 2 22
52 6232
42
x
11
71
33
31
21
51 61
41
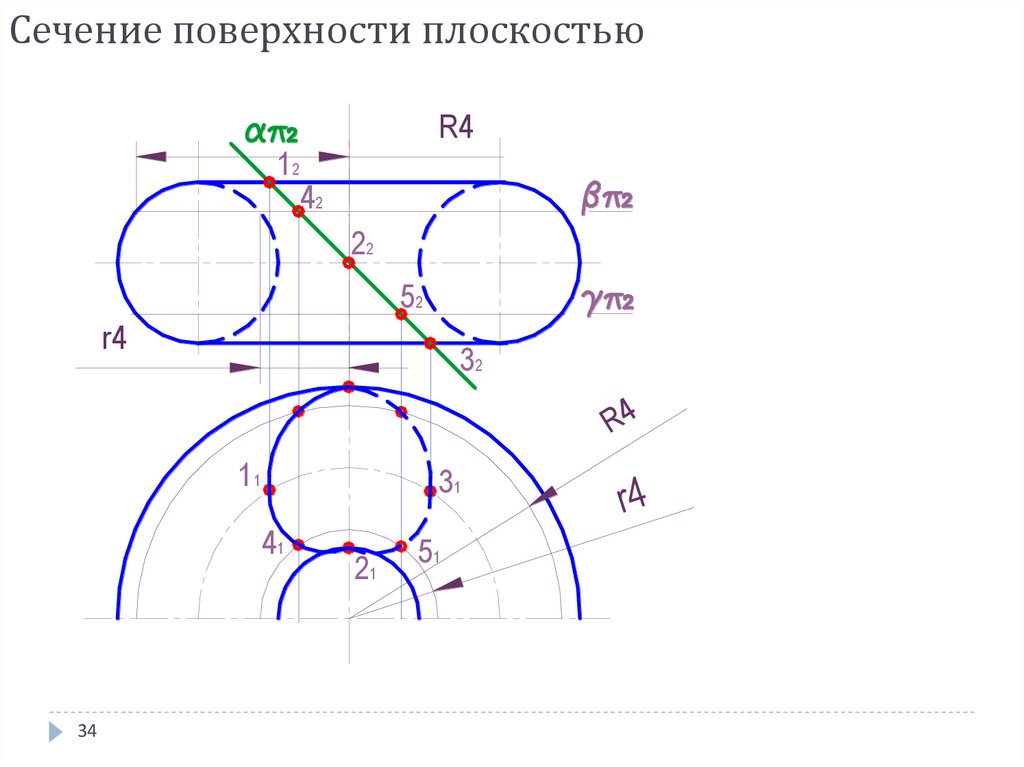
34. Сечение поверхности плоскостью
12R4
42
22
52
r4
32
R4
11
31
41
34
21
51
r4
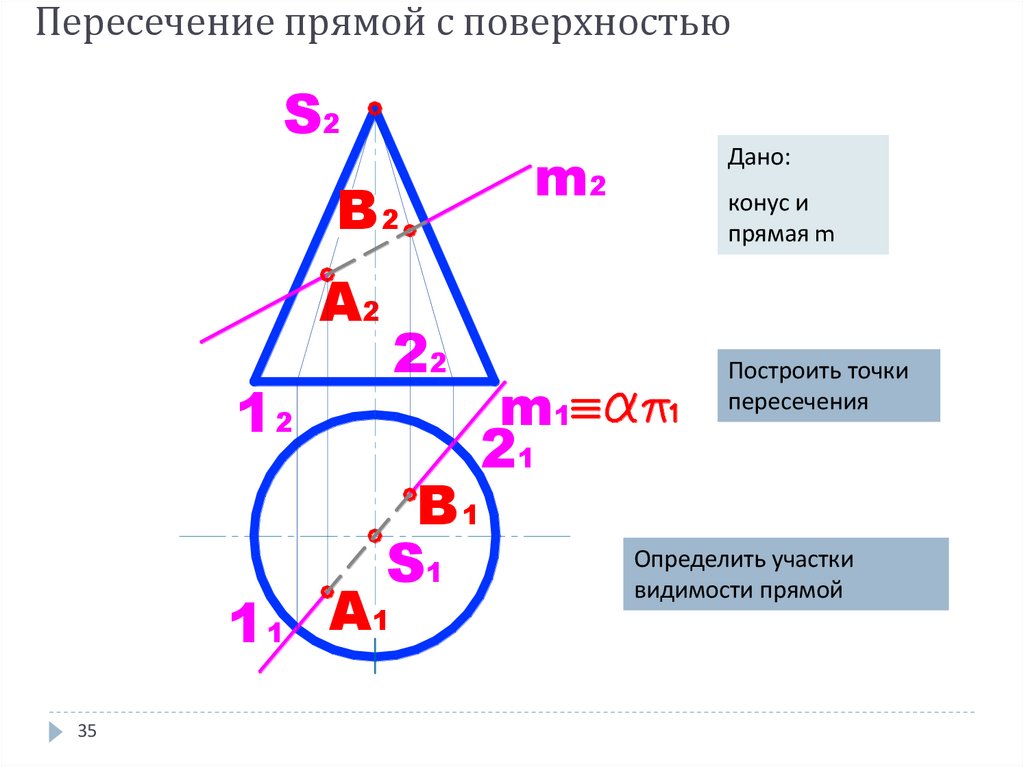
35. Пересечение прямой с поверхностью
2m2
B2
A2
22
12
m1
21
211
B
S1
1 1 A1
35
Дано:
конус и
прямая m
Построить точки
пересечения
Определить участки
видимости прямой
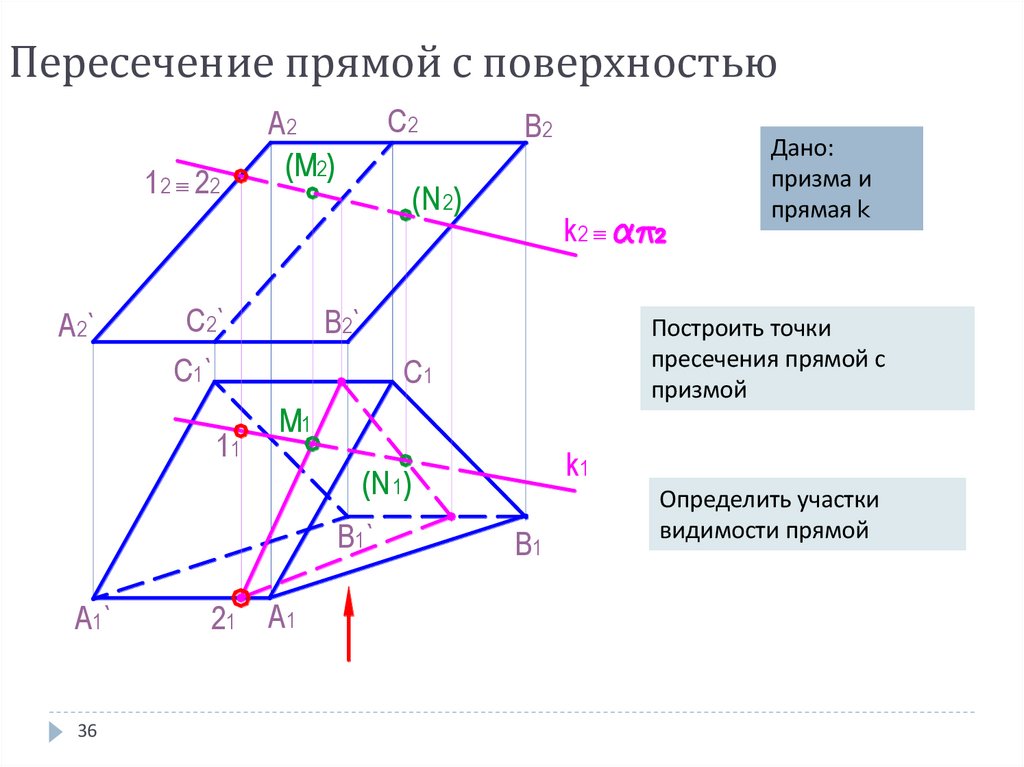
36. Пересечение прямой с поверхностью
1 2 22A2`
C2
A2
M
(M22)
C2`
N
(N22)
M
M11
N1
(N 1)
B1`
21 A1
Дано:
призма и
прямая k
Построить точки
пресечения прямой с
призмой
C1
11
36
k2
B2`
C1`
A1 `
B2
k1
B1
Определить участки
видимости прямой
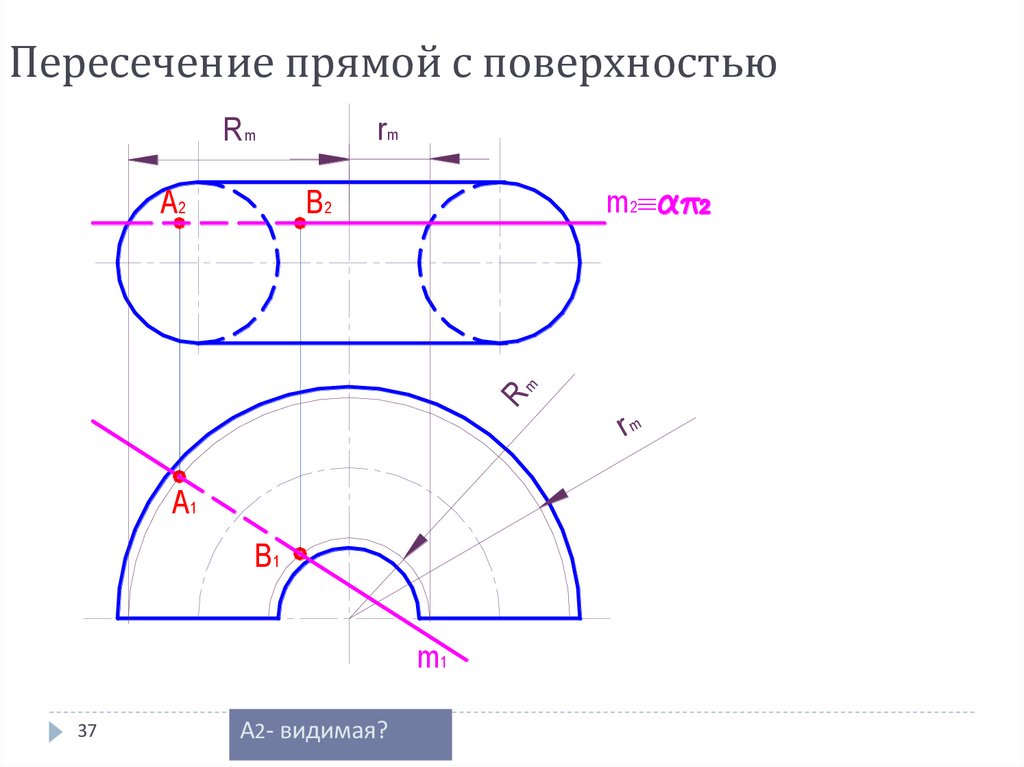
37. Пересечение прямой с поверхностью
rmRm
m2
B2
Rm
A2
A1
B1
m1
37
А2- видимая?
rm
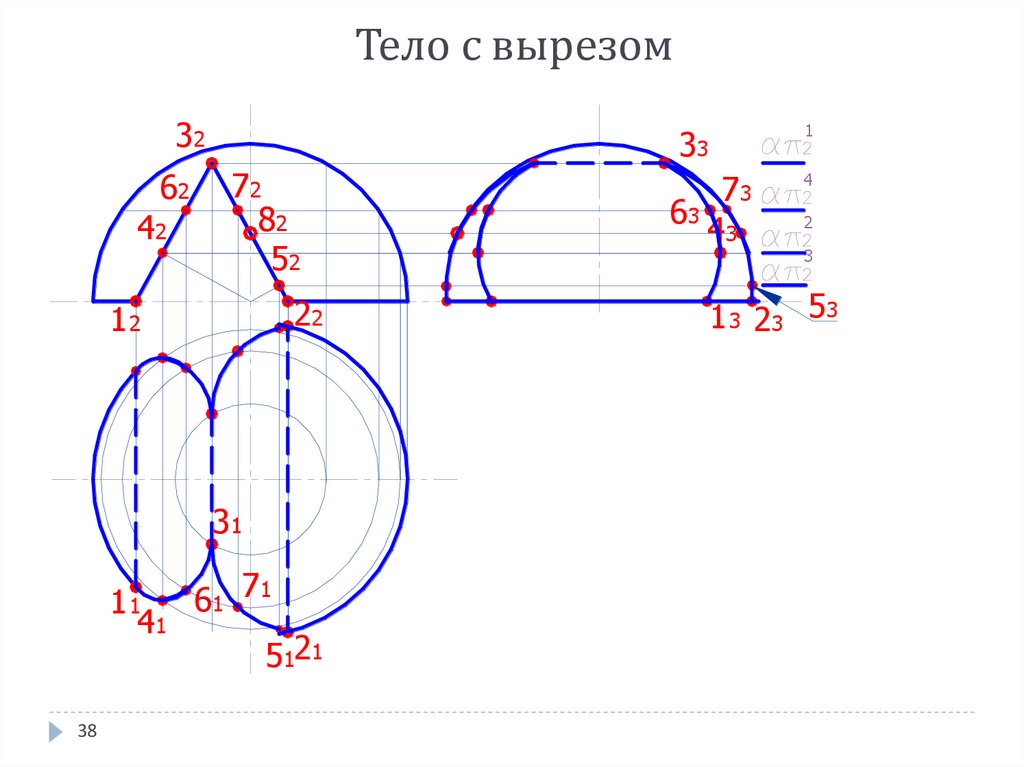
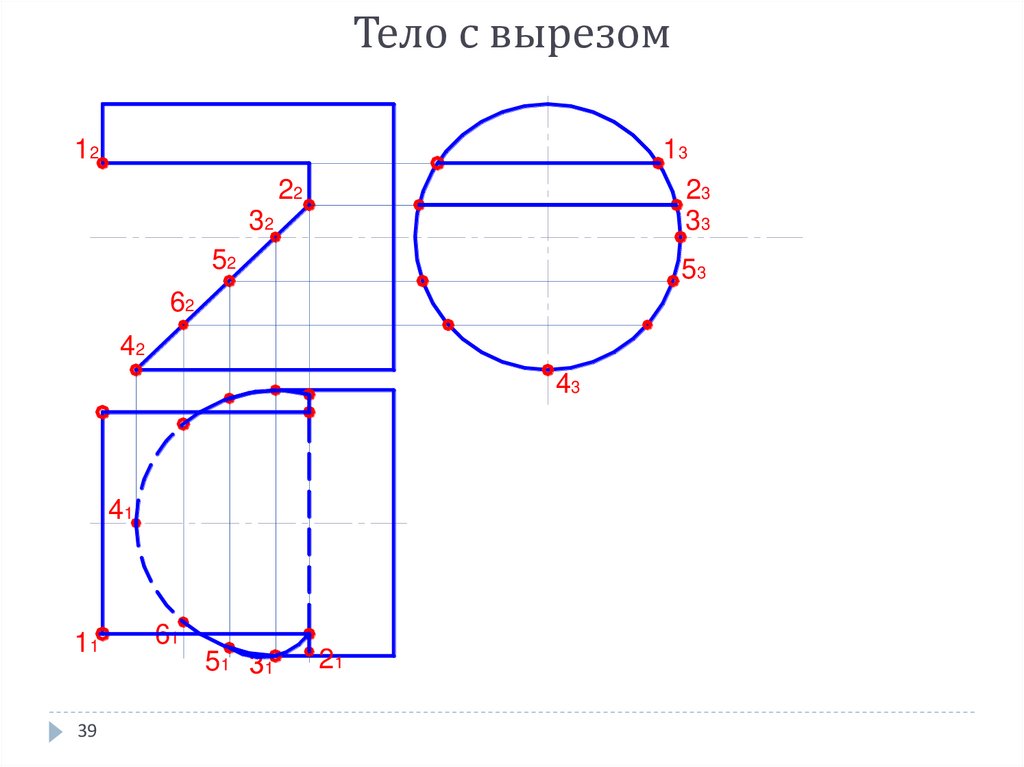
38. Тело с вырезом
3262
42
72
82
52
22
12
31
11
41
38
31
61 71
5121
33
1
73
63
43
4
2
3
1 3 23 53
39. Тело с вырезом
12y1
22
32
52
53
62
42
43 y2
yy65
y5
yy26
41
y1
11
39
61
51
13
23
33
1
21
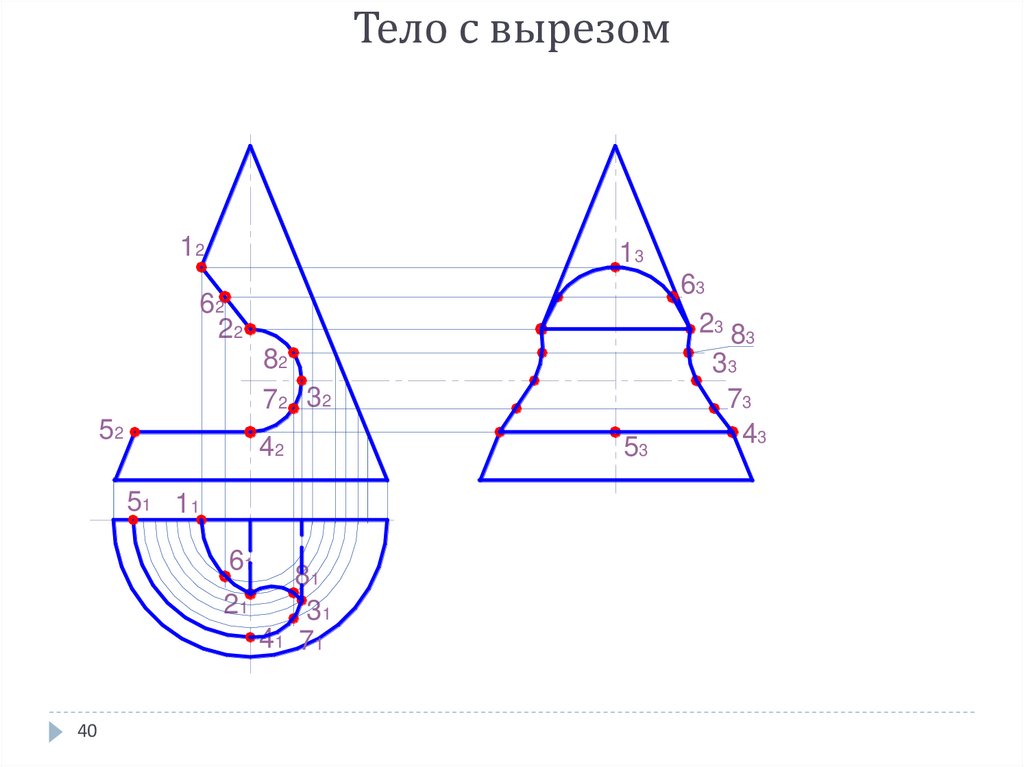
40. Тело с вырезом
1213
62
22
82
72 32
52
42
53
51 11
61
81
21
31
41 71
40
y386
y
y7
63
23 83
33
73
43
yyy6y837
41. ВЫВОДЫ
Построение проекций тела с вырезомвыполняется по правилам построения сечений
Здесь вместо одной секущей поверхности
(плоскости) даны несколько поверхностей
(плоскостей) формирующих контуры выреза
При построении необходимо построить
характерные точки
Определить видимость линий пересечения и
контуров объекта
41
42. ВЫВОДЫ
Одна проекция сечения на чертежесовпадает со следом секущей плоскости
Построение сечения следует начинать с
построения характерных точек
42
43. ВЫВОДЫ
Характерные точки:- точки, лежащие на крайних
образующих
- точки, определяющие границу
видимости
- точки максимального и
минимального удаления от плоскостей
проекций
43
44. ВЫВОДЫ
Использование вспомогательных секущихплоскостей в достаточном количестве позволяет
точнее построить линию сечения
Построение точек пересечения прямой с
поверхностью выполняется с помощью
вспомогательной секущей плоскости, совпадающей
с одной из проекций этой прямой
44
45. Контрольные вопросы
1.2.
3.
4.
45
Назовите порядок построения точек пересечения
прямой с поверхностью
Как определить видимость участков прямой при
пересечении поверхности
Какие сечения получаются при пересечении сферы,
тора, конуса, цилиндра
Как построить натуральную величину сечения?
46. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ
При пересечении поверхностей получается линия,которая одновременно принадлежит обеим
поверхностям
47. Пример пересечения призмы и сферы
Пересечениемногогранника и
кривой поверхности
дает сочетание
плоских кривых
линий (параболу,
гиперболу, эллипс и
т.д.)
47
48. Пример пересечения конуса и цилиндра
Пересечение двухкривых
поверхностей дает
пространственную
кривую линию
49. Пересечение поверхностей. Метод вспомогательных секущих плоскостей
1.2.
49
Анализ поверхности: определить наличие
проецирующей поверхности. В этом случае на
одной из плоскостей проекций уже имеется одна
проекция линии пересечения
Проведение вспомогательной секущей плоскости,
которая выбирается из условия получения в
сечении простых геометрических фигур –
окружностей, треугольников, прямоугольников
50. Пересечение поверхностей. Метод вспомогательных секущих плоскостей
3.4.
5.
50
Построение двух линий пересечения обеих
поверхностей вспомогательной секущей
плоскостью
При построении линий пересечения найти
характерные точки
Определение точек пересечения двух
построенных линий
51. Пересечение поверхностей. Метод вспомогательных секущих плоскостей
Повторение пунктов 2, 3, 4 – n разСоединение полученных точек
пересечения
линией
Определение видимости линий пересечения и линий
заданных поверхностей
6.
7.
8.
51
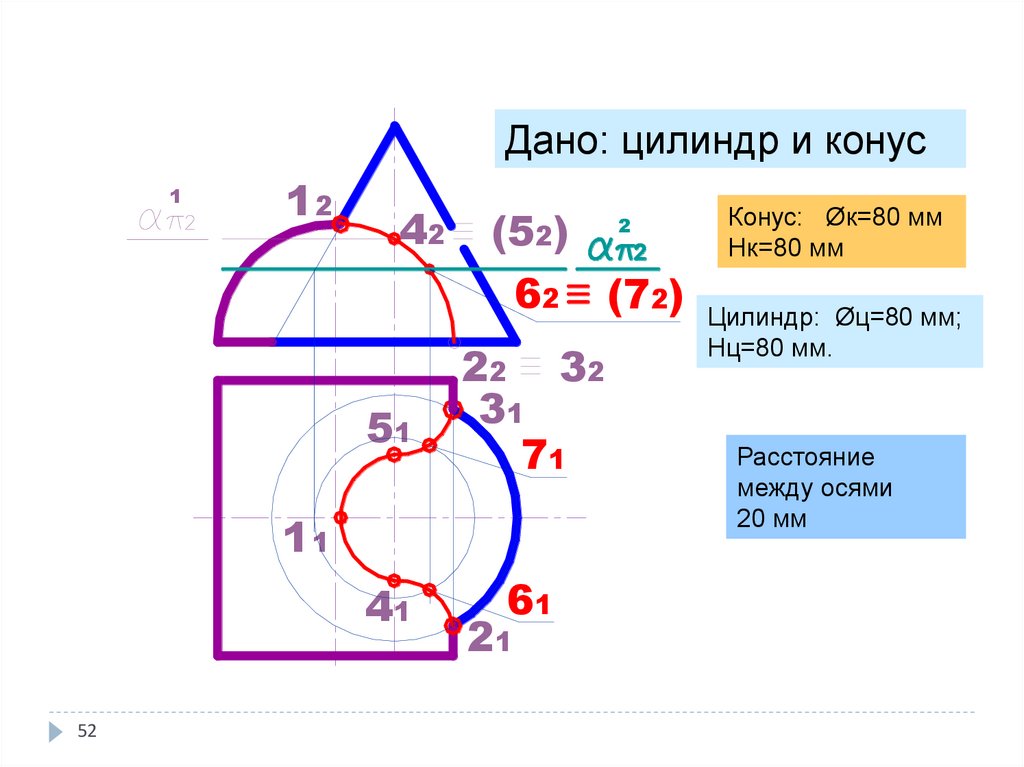
52. Метод вспомогательных секущих плоскостей
Дано: цилиндр и конус1
12
42
(52)
Конус: Øк=80 мм
Нк=80 мм
62
(72) Цилиндр: Øц=80 мм;
51
22 32
31
71
Нц=80 мм.
41
61
11
52
2
21
Расстояние
между осями
20 мм
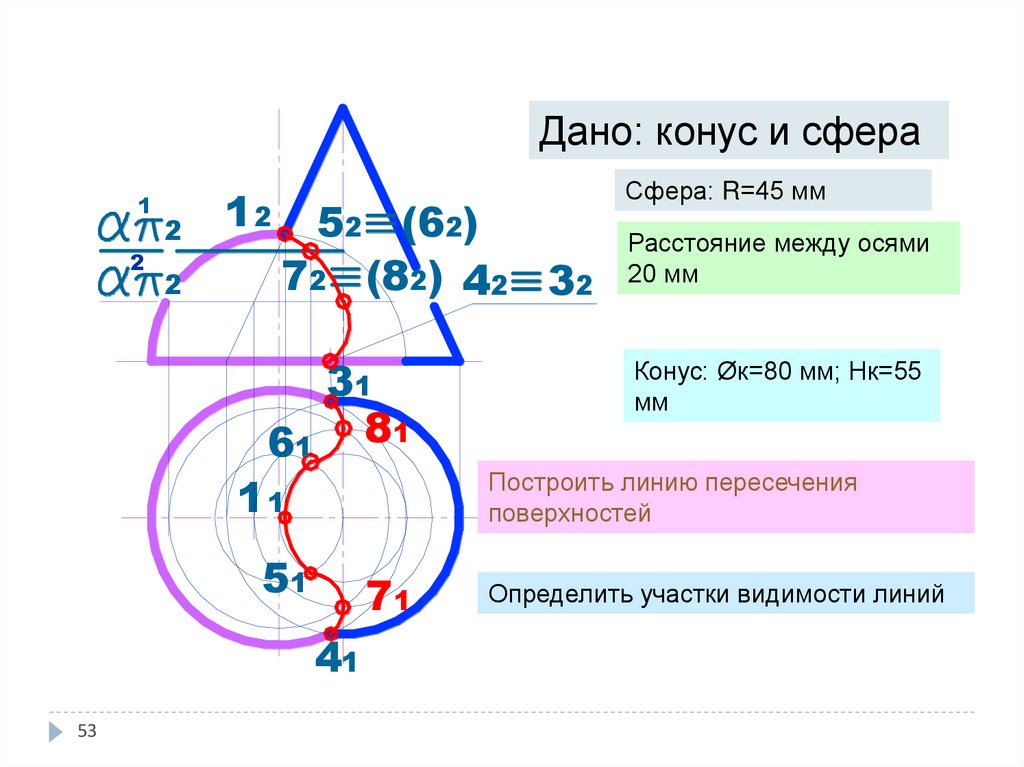
53. Метод вспомогательных секущих плоскостей
Дано: конус и сфера1
2
2
2
12
52 (62)
72 (82) 42 32
31
6161 81
11
51 71
51
53
Сфера: R=45 мм
Расстояние между осями
20 мм
Конус: Øк=80 мм; Нк=55
мм
Построить линию пересечения
поверхностей
Определить участки видимости линий
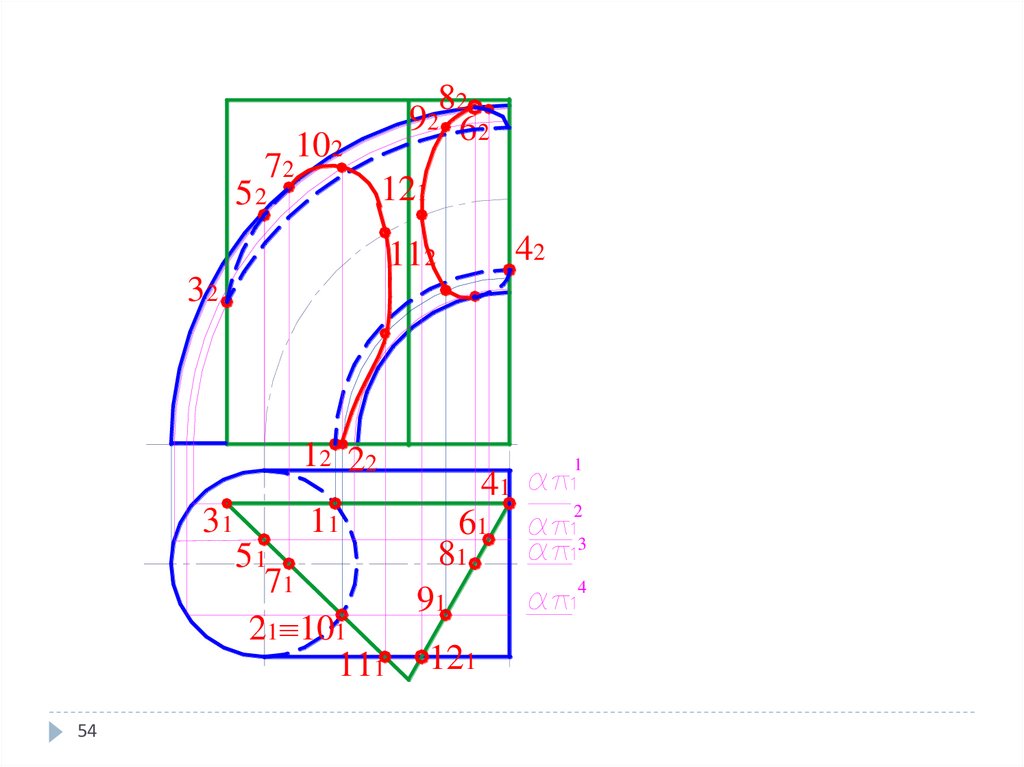
54. Метод вспомогательных секущих плоскостей
2 292926262
10
10
22
772 2
1212
11
552 2
1111
22
4242
332 2
11
2 22222
4141
331 1
1111
6161
81861 1
551 1
771 1
9191
221 10
1 10
21 11 101
1 1
1111
1 1 12
12
54
11 1
2 2
3 3
4 4
55. ВЫВОДЫ
Метод вспомогательных секущих плоскостейслужит для построения линий пересечения
различных поверхностей
Определение характерных точек и построение
достаточного количества вспомогательных
секущих плоскостей обеспечивает точность
построения линий пересечения поверхностей
При построении линии пересечения необходимо
также решать задачу определения видимости
участков прямой, используя метод
конкурирующих точек
55
56. Контрольные вопросы
1.2.
3.
Для каких поверхностей используется метод
вспомогательных секущих плоскостей?
На чем основывается данный метод?
Назовите основные пункты метода вспомогательных
секущих плоскостей
56
57. Контрольные вопросы
4.5.
В чем успех точности построения линии пересечения
поверхностей?
Как определить участки видимости линий чертежа?
57
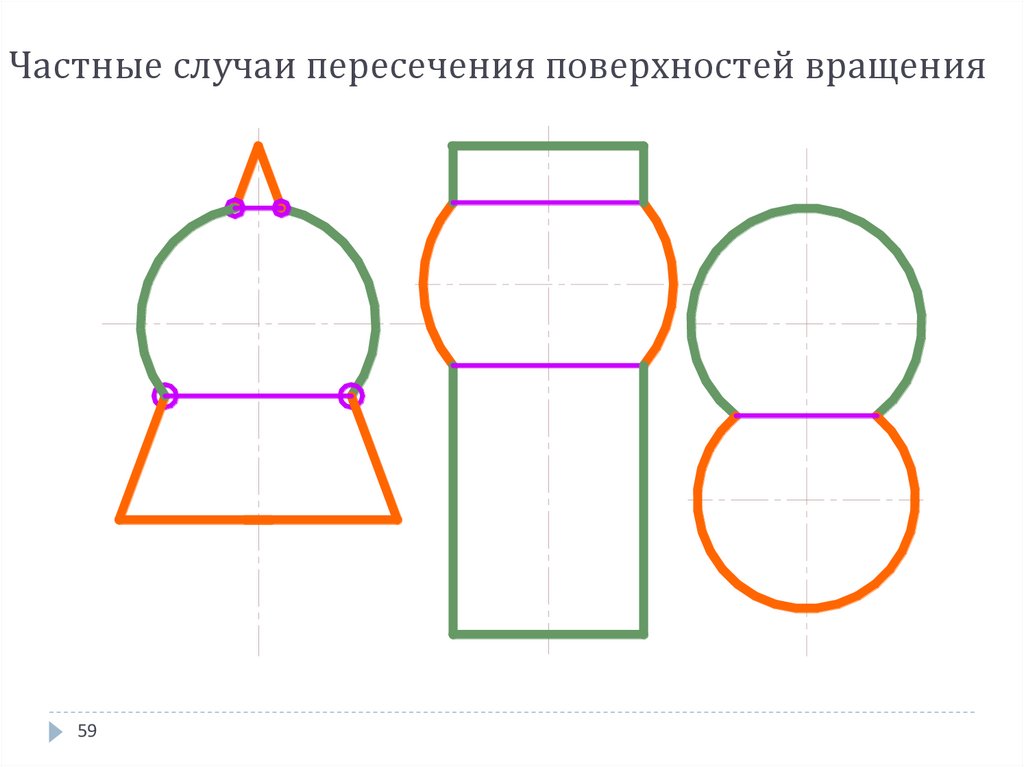
58. Частные случаи пересечения поверхностей вращения
Соосные поверхности - поверхности вращения,имеющие общую ось вращения
Все линии пересечения - окружности. На
плоскость проекций, параллельную осям
вращения, они проецируются в виде отрезка
прямой линии, соединяющего точки
пересечения очерковых образующих
58
59. Частные случаи пересечения поверхностей вращения
5960. Частные случаи пересечения поверхностей вращения
Теорема Монжа: две поверхности вращения,описанные вокруг третьей, пересекаются между
собой по двум кривым второго порядка, которые
проецируются на плоскость, параллельную осям
вращения в виде прямолинейных отрезков,
соединяющих точки пересечения очерковых
образующих
60
61. Частные случаи пересечения поверхностей вращения
6162. Метод вспомогательных концентрических сфер
• Преимущество:возможность построения линии
пересечения двух поверхностей в одной проекции
• Недостаток: ограничение области применения
следующими условиями:
1. Обе пересекающиеся поверхности -поверхности
вращения
2. Их оси вращения пересекаются
3. Оси вращения параллельны плоскости проекций
62
63. Метод вспомогательных концентрических сфер
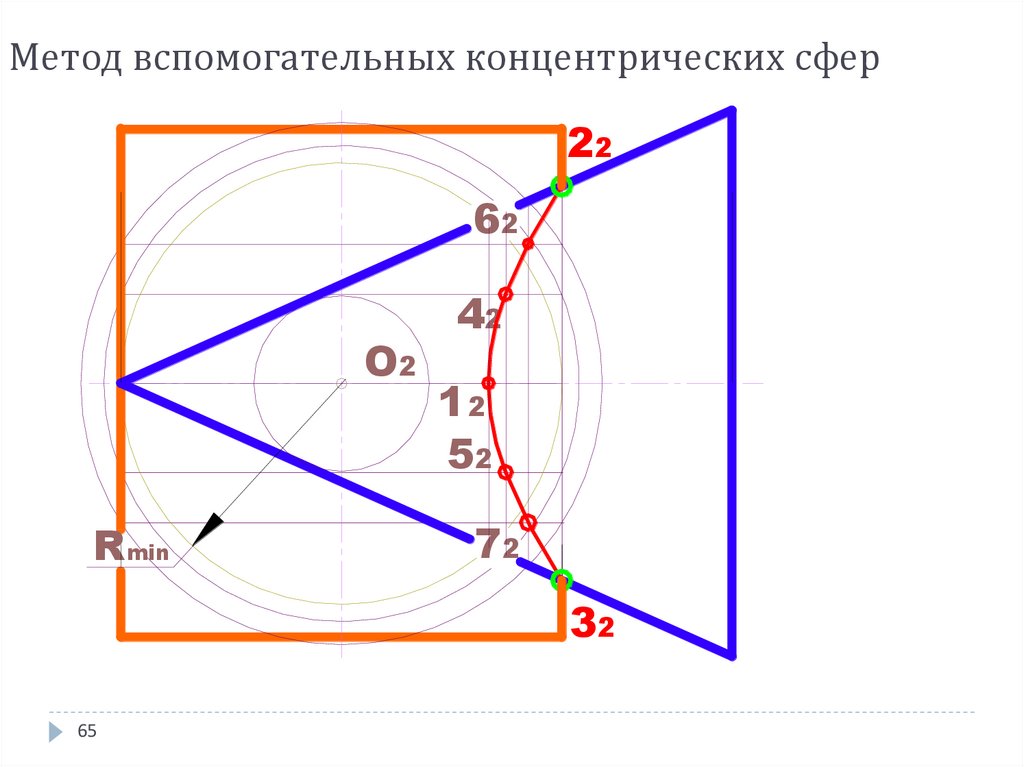
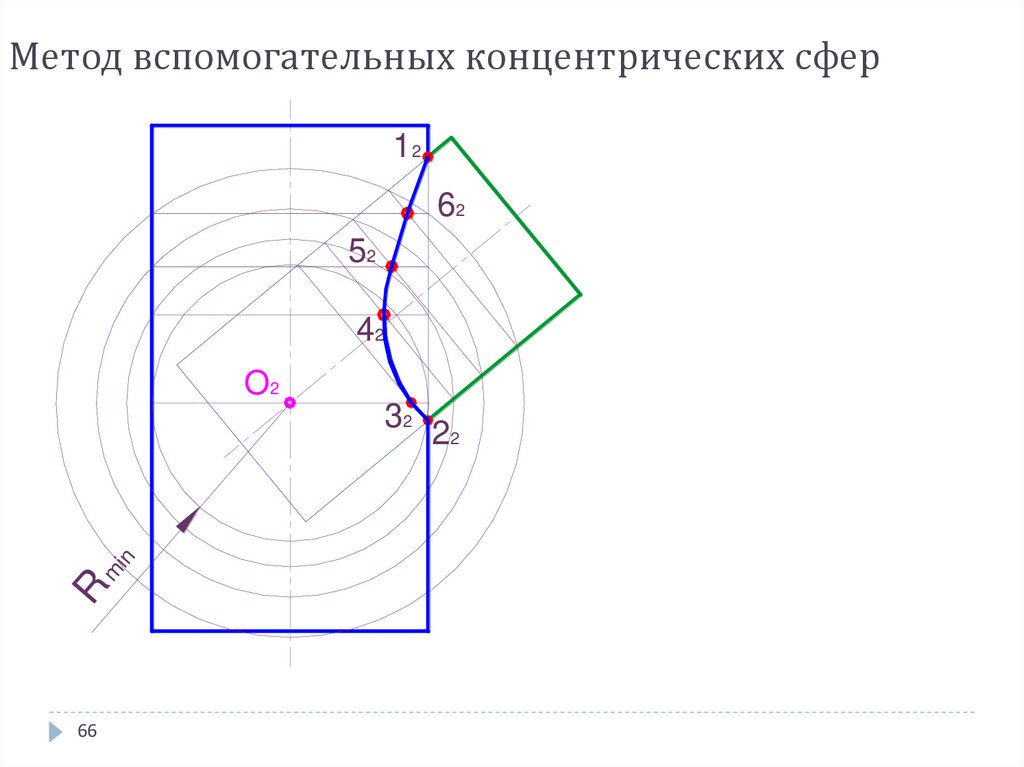
Порядок построения:1. Определить центр вспомогательных
концентрических сфер - это точка пересечения
осей вращения
2. Определить радиус минимальной вписанной
сферы - это максимальный из радиусов сфер,
вписанных в обе заданные поверхности
вращения
63
64. Метод вспомогательных концентрических сфер
3.4.
5.
64
Построить линии пересечения
вспомогательной сферы с обеими заданными
поверхностями. Линии пересечения окружности, которые проецируются в отрезки
прямой линии
Определить точки пересечения построенных
линий
Определить видимость линий выполненного
изображения
65. Метод вспомогательных концентрических сфер
22226622
OO22
min
RRmin
4422
1122
5522
7722
3322
65
66. Метод вспомогательных концентрических сфер
1262
52
42
R
m
in
O
O22
66
32
22
67. ВЫВОДЫ
• Метод концентрических сфер позволяет водной проекции построить линию
пересечения двух поверхностей
• Область использования этого метода
ограничена следующими требованиями:
- обе поверхности должны быть
поверхностями вращения
- их оси должны пересекаться
- их оси должны лежать в плоскости
параллельной плоскости проекций
67
68. Контрольные вопросы
1.2.
3.
68
Какие Вы знаете частные случаи пересечения
поверхностей вращения?
Как строится линия пересечения в этих случаях?
Для чего служит метод концентрических сфер?
69. Контрольные вопросы
4.5.
6.
7.
69
Достоинства метода концентрических сфер
Область использования метода
Какой радиус сферы называется минимальным?
Какие точки линии пересечения являются
характерными?




































 mathematics
mathematics








