Перпендикуляр и наклонные 2

1. Перпендикуляр и наклонные: расстояние от точки до плоскости, расстояние от прямой до плоско­сти.

Перпендикуляр и наклонные:
расстояние от точки до
плоскости, расстояние от
прямой до плоскости.
Подготовила:
учитель математики
МБОУ Г.ГОРЛОВКИ «ШКОЛА № 42»
Рыбина М.В.

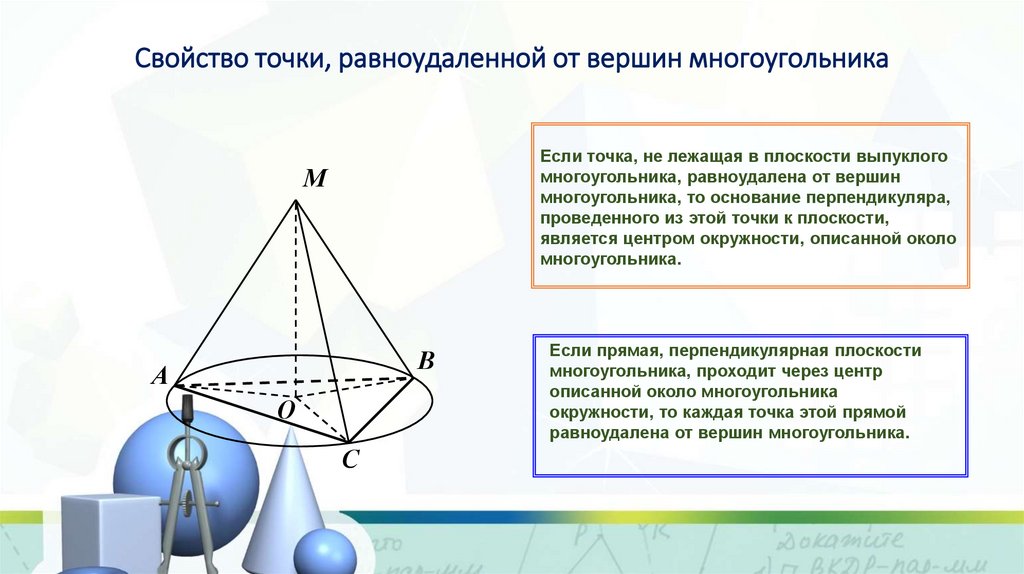
2. Свойство точки, равноудаленной от вершин многоугольника

Если точка, не лежащая в плоскости выпуклого
многоугольника, равноудалена от вершин
многоугольника, то основание перпендикуляра,
проведенного из этой точки к плоскости,
является центром окружности, описанной около
многоугольника.
М
В
А
О
С
Если прямая, перпендикулярная плоскости
многоугольника, проходит через центр
описанной около многоугольника
окружности, то каждая точка этой прямой
равноудалена от вершин многоугольника.

3. Окружность, описанная около многоугольника

Центр окружности - точка пересечения серединных
перпендикуляров со сторонами многоугольника.
Остроугольный
треугольник
Тупоугольный треугольник
Прямоугольный
треугольник
abc
R
4S
a
b
c
R
2 sin A 2 sin B 2 sin C
c
R
2
Правильный
треугольник
Квадрат
Правильный
шестиугольник
a
R
3
a
R
2
R=a

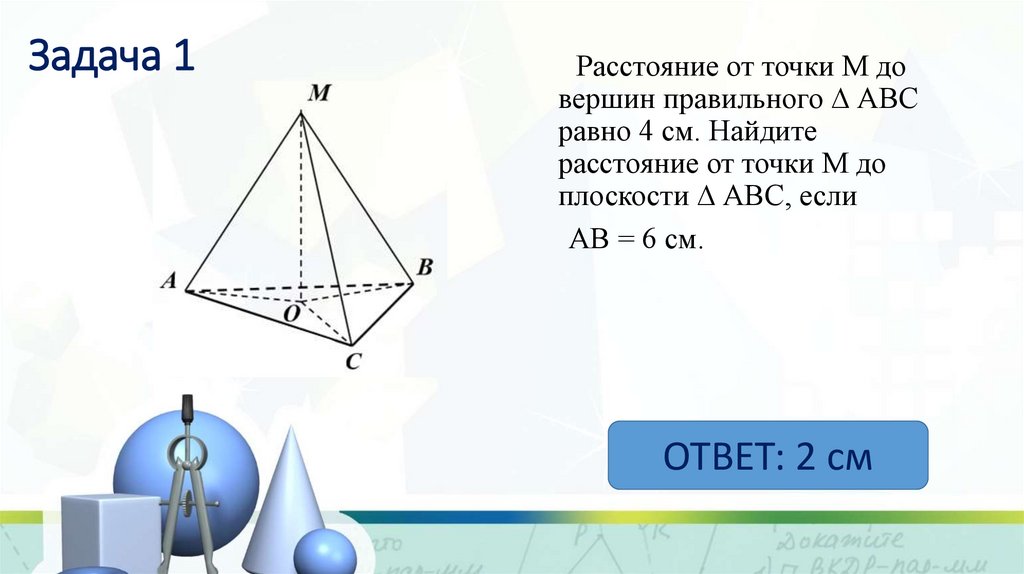
4. Задача 1

Расстояние от точки М до
вершин правильного АВС
равно 4 см. Найдите
расстояние от точки М до
плоскости АВС, если
АВ = 6 см.
ОТВЕТ: 2 см

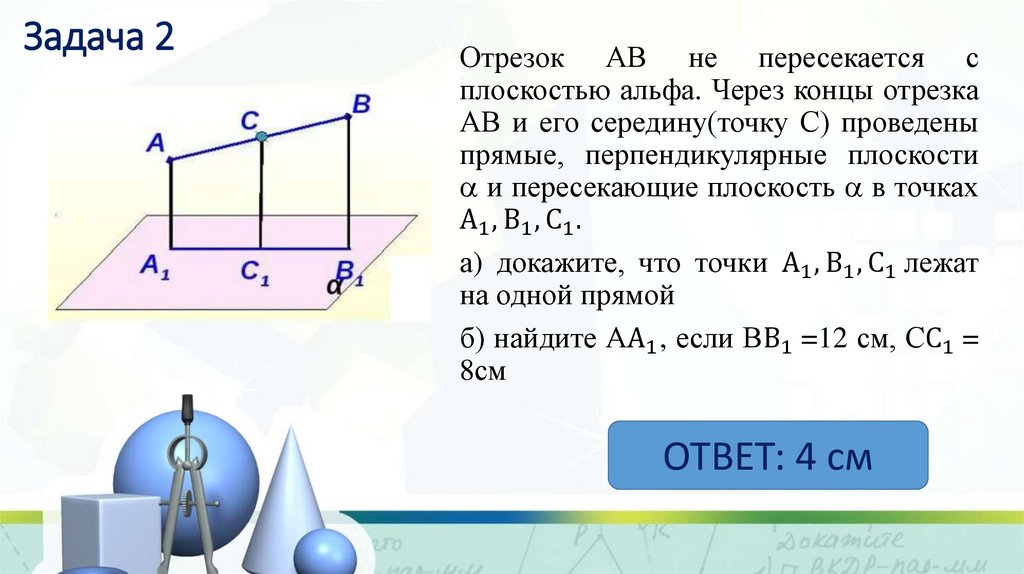
5. Задача 2

Отрезок АВ не пересекается с
плоскостью альфа. Через концы отрезка
АВ и его середину(точку С) проведены
прямые, перпендикулярные плоскости
и пересекающие плоскость в точках
А1 , В1 , С1 .
а) докажите, что точки А1 , В1 , С1 лежат
на одной прямой
б) найдите АА1 , если ВВ1 =12 см, СС1 =
8см
ОТВЕТ: 4 см

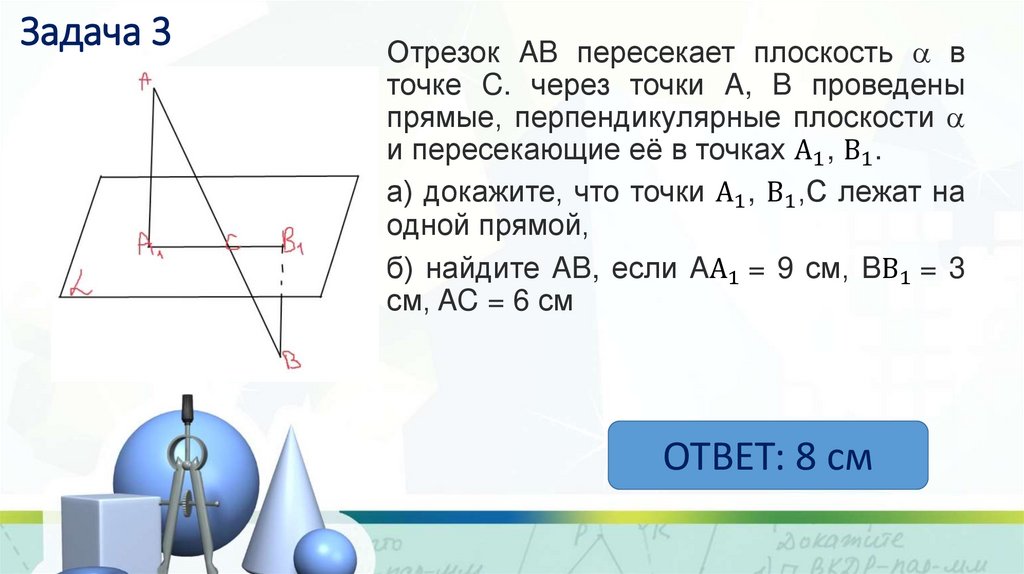
6. Задача 3

Отрезок AB пересекает плоскость в
точке C. через точки A, B проведены
прямые, перпендикулярные плоскости
и пересекающие её в точках А1 , В1 .
а) докажите, что точки А1 , В1 ,С лежат на
одной прямой,
б) найдите AB, если AА1 = 9 см, BВ1 = 3
см, AC = 6 см
ОТВЕТ: 8 см

7. Задача 4

Точка М лежит на отрезке АВ.
Отрезок
АВ
пересекается
с
плоскостью в точке В. Через А и М
проведены
прямые,
перпендикулярные плоскости и
пересекающие её в точках А1 и М1 .
а) Докажите, что А1 , М1 , и В лежат на
одной
прямой.
б) Найдите длину отрезка АВ,
если АА1 : ММ1 = 3:2, АМ = 6 см
ОТВЕТ: 18 см

8. Задача 5

Из точки А, не принадлежащей
плоскости
,
проведены
на
плоскость
перпендикуляр
и
наклонная. Длина перпендикуляра
12 см, длина наклонной 13 см.
Найдите
длину
проекции
наклонной на плоскость
ОТВЕТ: 5 см

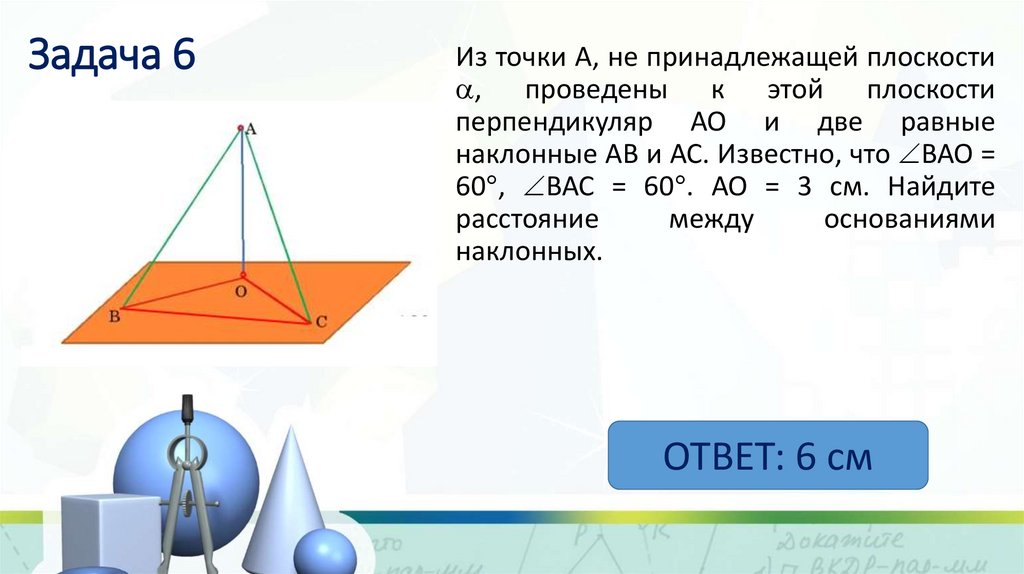
9. Задача 6

Из точки А, не принадлежащей плоскости
, проведены к этой плоскости
перпендикуляр АО и две равные
наклонные АВ и АС. Известно, что ВАО =
60 , ВАС = 60 . АО = 3 см. Найдите
расстояние
между
основаниями
наклонных.
ОТВЕТ: 6 см

10. Задача 7

Из точки , не принадлежащей данной
плоскости, проведены к ней две наклонные
, равные 10 см и 18 см. Сумма длин их
проекций на плоскость равна 16 см. Найти
проекцию каждой наклонной.
ОТВЕТ: 1 см и 15 см

11. Задача 8

Из точки А, взятой вне плоскости ,
проведены к ней равные наклонные АВ
и
АС.
Расстояние
ВС
между
основаниями наклонных равно 10 см.
Угол между ВС и АВ равен 60 , угол
между ВС и проекцией наклонной АВ
на плоскость равен 30 . Найдите
расстояние от точки А до плоскости .
ОТВЕТ: 10
2
см
3

12. Домашнее задание

Повторить правила § 2, п.19
Выполнить в тетради № 141, 142