Лекция_14_формулы_03.12.2024

1. Лекция №14 Разработка программного обеспечения для моделирования физических процессов

Санкт-Петербургский политехнический университет Петра Великого
Лекция №14
Разработка программного обеспечения для
моделирования физических процессов
Воскобойников С.П.
Доцент ВШ ПИ ИКНК, к.ф.-м.н.
voskob_sp@spbstu.ru
03.12.2024

2. Содержание

• Итерационные методы решения линейных систем
уравнений. Метод простой итерации, Якоби и
Гаусса-Зейделя. Матричная запись.
• Каноническая схема одношагового итерационного
метода. Классификация методов.
• Уравнение для погрешности. Сходимость. Число
итераций.
• Необходимое и достаточное условие сходимости
стационарного итерационного метода и его
оптимизация.
• Идея предобусловливания.
• Вариационные методы. МСС, НМСС, ММН,
НММН.

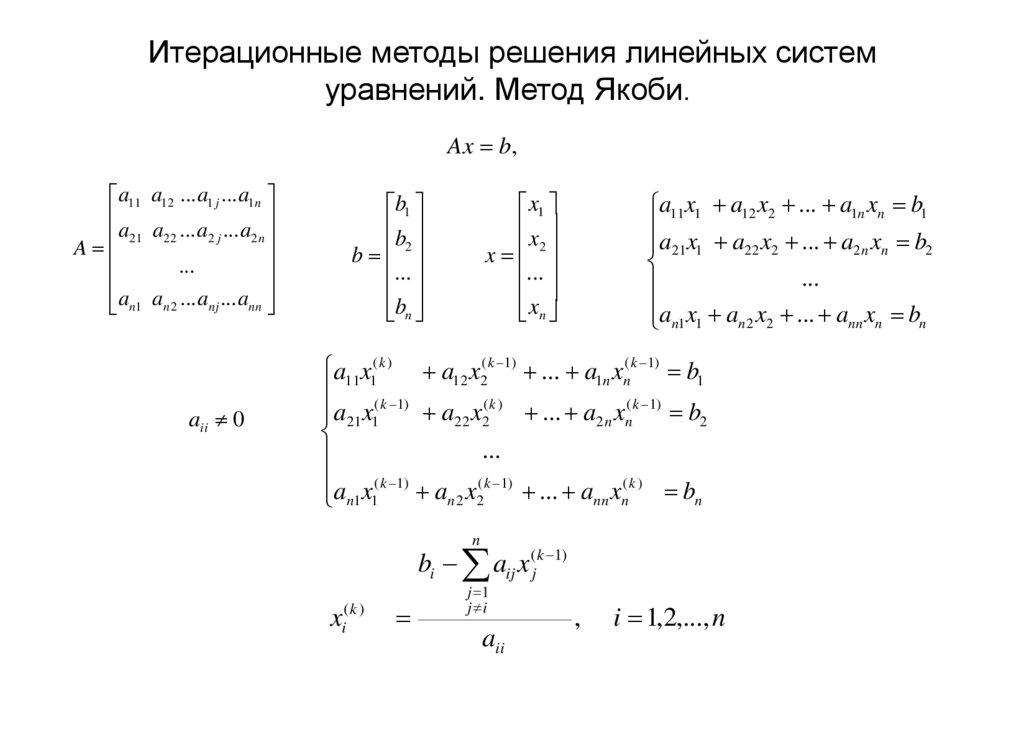
3. Итерационные методы решения линейных систем уравнений. Метод Якоби.

Ax b,
a11 a12 ... a1 j ... a1n
a
a
...
a
...
a
21
22
2j
2n
A
...
an1 an 2 ... anj ... ann
aii 0
b1
b
b 2
...
bn
a11x1 a12 x2 ... a1n xn b1
a x a x ... a x b
21 1
22 2
2n n
2
...
an1 x1 an 2 x2 ... ann xn bn
x1
x
x 2
...
xn
a11x1( k ) a12 x2( k 1) ... a1n xn( k 1) b1
( k 1)
a22 x2( k ) ... a2 n xn( k 1) b2
a21x1
...
a x ( k 1) a x ( k 1) ... a x ( k ) b
n2 2
nn n
n
n1 1
n
bi aij x (jk 1)
(k )
i
x
j 1
j i
aii
,
i 1,2,..., n

4. Итерационные методы решения линейных систем уравнений. Метод Якоби и Гаусса-Зейделя.

Ax b,
0 0
...
0
a
0
...
0
21
L a31 a32 0 ...
0
...
a a
n1 n 2 ... an , n 1 0
A L D U
a11
a
22
D
...
Lx Dx Ux b
Lx Dx b Ux
Dx Lx Ux b
L D x b Ux
Dx ( k ) Lx( k 1) Ux( k 1) b, x(0) ,
k 1,2,...
Dx ( k ) Dx ( k 1) Lx( k 1) Dx ( k 1) Ux( k 1) b,
ann
0 a12 a13 ... a1n
0 0 a23 ... a2 n
U
...
0
...
0
a
n 1, n
0
...
0
D x( k ) x( k 1) Ax( k 1) b, x(0) ,
k 1,2,...
L D x( k ) b Ux( k 1)
L D x( k ) L D x( k 1) b L D x( k 1) Ux( k 1)
L D x( k ) x( k 1) b Ax( k 1)

5. Итерационные методы решения линейных систем уравнений. Методы релаксации.

Ax b,
0 0
...
0
a
0
...
0
21
L a31 a32 0 ...
0
...
a a
n1 n 2 ... an , n 1 0
A L D U
a11
a
22
D
...
0 a12 a13 ... a1n
0 0 a23 ... a2 n
U
...
0
...
0
a
n 1, n
0
...
0
ann
Ax b,
Dx Lx Ax Dx Lx b,
D L x D L x b Ax ,
D L x( k 1) D L x( k ) b Ax( k ) ,
D L x
( k 1)
x(k )
Ax
(k )
b,
0 2

6. Методы простой итерации с параметром.

Ax b,
x x Ax b
x x Ax b
x ( k ) x ( k 1) Ax( k 1) b
x ( k ) x ( k 1)
Ax( k 1) b

7. Каноническая схема одношагового итерационного метода

Ax b,
Bk
x ( k ) x ( k 1)
k
Ax( k 1) b, x 0 , k 1,2,...
Bk , k
Bk E,
Bk B, k
Bk E, k 1
Bk E, k
Bk D, k 1
Bk L D, k 1
Bk L D, k ,
0 2

8. Каноническая схема одношагового итерационного метода

Ax b,
Bk
x ( k ) x ( k 1)
k
Ax( k 1) b, x 0 , k 1,2,...
Az k r k , z k x x k
Bk
x x ( k ) x x ( k 1)
k
Bk
x 0
z ( k ) z ( k 1)
k
Ax( k 1) b 0, x 0 , k 1,2,...
Az ( k 1) 0, z 0 , k 1,2,...
lim z ( k ) 0
k

9. Каноническая схема одношагового итерационного метода

Ax b,
Bk
Bk
x ( k ) x ( k 1)
Ax( k 1) b, x 0 , k 1,2,...
k
z ( k ) z ( k 1)
k
Az ( k 1) 0, z 0 , k 1,2,...
z ( k ) E k Bk 1 A z ( k 1) , z 0 , k 1,2,...
Sk q 1
S k E k Bk 1 A
z ( k ) S k z ( k 1)
z ( k ) q k z (0)
z (k )
z
ln 1 /
k
1
ln
1
/
q
k
q
(0)
R ln 1/ q , q 1

10. Схема применения одношагового итерационного метода

Ax b,
Bk
x 0
x ( k ) x ( k 1)
k
Ax( k 1) b, x 0 , k 1,2,...
b Ax( k ) b Ax( k 1) A ( k )
k 1,2,...
r ( k 1) b Ax ( k 1) ,
r ( k ) r ( k 1) A ( k )
k ?
( k ) x ( k ) x ( k 1)
Bk ( k ) k r ( k 1) ,
Bk ( k ) k r ( k 1) , x 0 ,
x ( k ) x ( k 1) ( k )
x 0 ,
r ( 0 ) b Ax( 0 ) ,
k 1,2,...
k ?
Bk ( k ) k r ( k 1) ,
k 1,2,...
x ( k ) x ( k 1) ( k )
r ( k ) r ( k 1) A ( k )

11. Необходимое и достаточное условие сходимости стационарного итерационного метода

Ax b,
B
x ( k ) x ( k 1)
Ax( k 1) b, x 0 , k 1,2,...
z ( k ) E B 1 A z ( k 1) , z 0 , k 1,2,...
i S 1 i B 1 A
S E B 1 A
i S 1,
lim z ( k ) 0,
k
B 1 A V V 1
z ( k ) E V V 1 z ( k 1) ,
w( k ) V 1 z ( k )
1 i B 1 A 1,
z ( k ) V E V 1z ( k 1) ,
w( k ) E w( k 1) ,
lim wi( k ) 0,
k
V 1z ( k ) E V 1z ( k 1) ,
wi( k ) 1 i B 1 A wi( k 1) , i 1,2,..., n
z
(k )
Vw
(k )
lim zi( k ) 0, i 1,2,...n
k

12. О собственных числах двух матриц

A AT , i A 0
1
2
B B B
B BT , i B 0
1
2
12 12
i B A i B AB
1
B 1 Ax x,
1
2
1
2
1
2
1
2
B AB B x B x,
1
2
1
2
B AB y y,
1
2
y B x,
1
1
B A B A
T
1
2
1
2
C B AB ,
C C T , i C 0, xT Cx 0, x 0

13. Оптимизация стационарного одношагового метода

z
1
2
(k )
B z
(k )
E B A z
1
( k 1)
,
1
1
1
2
2
E B AB B 2 z ( k 1) ,
1
2
1
1
1
2
2
z B E B AB B 2 z ( k 1) ,
1
1
1
(k )
y E B 2 AB 2 y ( k 1) ,
(k )
2 (k )
y B z
(k )
1
2
C B AB ,
1
2
1 i C 1

14. Оптимизация стационарного одношагового метода

1 opt min C 1 opt max C
max C
1
max C min C min C
opt 1 min C
max C min C max C 1
min C
1
1
2 C
opt
1
1
1
2 C
2
opt
max C min C
2 C
max C
min C
y ( k ) E C y ( k 1) opt y ( k 1) ,
2
2
2
y
(k )
k
y ( k ) opt
y ( 0) ,
2
1
2
B z
2
2
1
2
1
2
k
B z ( k ) opt
B z (0) ,
(k )
2
1
1
(k )
2 (k )
2 (k )
B z
B z ,B z
2
1
2
Bz , z z
(k )
(k )
lim z ( k )
(k )
B
k
2
B
0,

15. Идея предоубусловливания (неявности)

Ax b,
A AT , i A 0
B 1 Ax B 1b,
B BT , i B 0
1
2
1
2
1
2
1
2
B AB B x B b,
1
2
1
2
C B AB ,
1
2
y B x,
1
2
d B b,
Cy d ,
2 C 2 A
B A, 2 A 1, k 1
Bw r
B A,

16. Одношаговые вариационные методы

Ax b,
B
x ( k ) x ( k 1)
k
(k )
z ( k ) E k B 1 A z ( k 1) , z 0 ,
J Dz , z
i D 0
D D ,
T
Ax( k 1) b, x 0 , k 1,2,...
z
(k )
k 1,2,...
J min,
(k ) 2
dJ
0,
d k
k
D
dz ( k ) ( k ) ( k ) dz ( k )
dz ( k ) ( k )
dJ
d
(k )
(k )
2 D
Dz , z D
, z Dz ,
, z
d k d k
d k
d k
d k
dz ( k ) ( k ) d
D
, z D
E k B 1 A z ( k 1) , E k B 1 A z ( k 1) DB 1 Az ( k 1) , z ( k 1) k B 1 Az ( k 1)
d k
d k
DB 1 Az( k 1) , z ( k 1) k DB 1 Az( k 1) , B 1 Az( k 1) 0
DB Az
1
k
,
, B Az
( k 1)
, z ( k 1)
DB Az
( k 1)
( k 1)
1 ( k 1)
1
w
B r
1
,
( k 1)
Bw
r
( k 1)
( k 1)
Az
r
( k 1)
( k 1)
,
DB r
,z
,
DB r , B r
Dw , z
Dw , w
1 ( k 1)
,
k
k
1 ( k 1)
( k 1)
1 ( k 1)
( k 1)
( k 1)
( k 1)
( k 1)

17. Сходимость одношаговых вариационных методов.

J Dz ( k ) , z ( k ) z ( k )
2
D
Dz
Dz ( k 1) , z ( k 1)
Dz
D z ( k 1) k w( k 1) , z ( k 1) k w( k 1)
( k 1)
,z
( k 1)
Dw
2 Dw
wDw , Dz, w Dz
( k 1)
( k 1)
( k 1) 2
( k 1)
( k 1)
1
2
1
2
x D w( k 1) , y D z ( k 1)
2
( k 1)
( k 1) 2
w
,
Dz
( k 1)
, z ( k 1) 1
,
( k 1)
( k 1)
( k 1)
( k 1)
Dw
,
w
Dz
,
z
12 ( k 1) 12 ( k 1)
2
D w ,D z
2
x, y x, y 1,
2
2
( k 1) 2
( k 1) 2
x
y
x 2 y 2
w
z
2
2
D
, z ( k 1) 2 k Dz ( k 1) , w( k 1) k2 Dw ( k 1) , w( k 1)
, z ( k 1)
Dw ( k 1) , z ( k 1)
( k 1)
( k 1)
Dz
,w
Dw ( k 1) , w( k 1)
2
( k 1)
( k 1)
,w
Dw ( k 1) , w( k 1)
2
1
1
( k 1)
( k 1)
2
2
D w ,D z
q z ( k 1) 2 ,
(k ) 2
( k 1) 2
z
z
1
D
D
D
( k 1) 2
( k 1) 2
w
z
D
D
2
D
( k 1)
q 1,
D D T , D 0
1
ln
n 1,
1
ln
q
1
2 B 1 A
q
,
1
1
2 B 1 A
1

18. Одношаговые вариационные методы. НМСС и ММС.

Ax b,
D A,
A AT , i A 0
Aw
Aw
( k 1)
k
B
x ( k ) x ( k 1)
k
x 0 ,
Ax( k 1) b, x 0 , k 1,2,...
k 1,2,...
w
Aw
( k 1)
x
( k 1)
,r
( k 1)
, w( k 1)
x
x ( k ) x ( k 1) k B 1 b Ax ( k 1) ,
( k 1)
kw
B E, w( k 1) r ( k 1) ,
x 0 ,
B w( k 1) r ( k 1) ,
(k )
x ( k ) x ( k 1) k w( k 1)
r ( 0 ) b Ax( 0 ) ,
k
, z ( k 1)
w( k 1) , r ( k 1)
( k 1)
( k 1)
,w
Aw( k 1) , w( k 1)
r ( 0 ) b Ax ( 0 ) ,
k 1,2,...
( k 1)
r ( k ) r ( k 1) k Aw( k 1)
r
Ar
( k 1)
k
, r ( k 1)
( k 1)
, r ( k 1)
x ( k ) x ( k 1) k r ( k 1)
r ( k ) r ( k 1) k Ar ( k 1)

19. Одношаговые вариационные методы. НММН и ММН

Ax b,
Dw
Dw
D AT A,
y 0,
A AT
, z ( k 1)
AT Aw( k 1) , z ( k 1)
Aw( k 1) , Az ( k 1)
Aw( k 1) , r ( k 1)
T ( k 1) ( k 1)
( k 1)
( k 1)
( k 1)
( k 1)
,w
A Aw , w
Aw , Aw
Aw( k 1) , Aw( k 1)
k
( k 1)
Ay, y 0,
B E, w( k 1) r ( k 1) ,
x 0 ,
r ( 0 ) b Ax ( 0 ) ,
k 1,2,...
Bw
( k 1)
k
x
r
(k )
(k )
r
Aw
( k 1)
( k 1)
r
r ( 0 ) b Ax ( 0 ) ,
k 1,2,...
,
( k 1)
,r
Aw( k 1) , Aw( k 1)
( k 1)
kw
( k 1)
k Aw
x
x 0 ,
( k 1)
( k 1)
Ar
Ar
k
( k 1)
, r ( k 1)
( k 1)
, Ar ( k 1)
x ( k ) x ( k 1) k r ( k 1)
r ( k ) r ( k 1) k Ar ( k 1)

20. О критериях остановки итерационных методов

Ax b,
x ( k ) x ( k 1) k r ( k 1)
r
r (k )
,
(k )
b
z (k )
x
A
r (k )
b
z (k )
,
r ( k ) r ( k 1) k Ar ( k 1) ,
x
r (k )
b
,
,
A ,
b Ax ( k )
b
b Ax ( k )
b
A 1,
,
stop
,
x (0) x ( k )