Similar presentations:
1_1 Множества_Функции25
1. ВЫСШАЯ МАТЕМАТИКА
Лектор Пыжкова Ольга Николаевнаауд. 205-4
2.
Список рекомендуемой литературы1.
2.
3.
4.
5.
6.
7.
8.
Высшая математика. В 2 ч.: учеб. пособие для студентов высших
учебных заведений по техническим специальностям / под ред.
В.М. Марченко. – Минск: БГТУ, ч. 1 – 2010, ч. 2 – 2014.
Гусак А.А. Высшая математика. В 2-х т. – Минск: Тетрасистемс,
1998-2009.
Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики.
– М.: АСТ, 1975-2008.
Письменный Д.Т. Конспект лекций по высшей математике: в 2 ч. –
М.: Айрис-пресс, 2003-2013.
Пискунов Н.С. Дифференциальное и интегральное исчисления для
втузов: в 2 т. – М.: Интеграл-Пресс, 1970-1985.
Шипачев В.С. Высшая математика: учеб. для немат. спец. вузов. –
М.: Высшая школа, 1985-2011.
Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в
упражнениях и задачах: в 2 ч. – М.: Оникс, 1980-2008.
Руководство к решению задач по высшей математике: в 2 ч. / под
общ. ред. Е.И. Гурского. – Минск: Вышэйшая школа, 1989.
3.
Раздел 1. ВВЕДЕНИЕ ВМАТЕМАТИЧЕСКИЙ АНАЛИЗ.
4.
§ 1. Множества.Основные числовые множества
Опр.1. Под множеством понимают совокупность
некоторых объектов, объединенных по какому-либо признаку.
Объекты, из которых состоит множество, называют его
элементами.
Обозначают: А, В,…Х, У, … – множества;
а, b,…, х, у…– элементы множества.
Множества обычно задают перечислением или описанием
свойств его элементов:
A {a1 , a2 , ..., an , ...};
S – множество студентов первого курса;
D = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} – множество цифр.
Обозначают: для описания множества, состоящего из тех
элементов множества Х, которые обладают свойством F(x),
используют запись: x F x , x X
или x : F x , x X .
5.
Обозначают:a A
b A
– объект a является элементом множества А;
– объект b не является элементом множества А.
Например, 1 1; 0;1; 2 , 4 1; 0;1; 2 .
Опр.2. Множество, не содержащее ни одного элемента,
называется пустым и обозначается символом .
Опр.3. Множества А и В называются равными (обозначается
А = В), если они состоят из одних и тех же элементов.
Опр.4. Множество А называется подмножеством
множества В, если каждый элемент множества А является
элементом множества В, обозначается: A B.
Считается, что пустое множество является подмножеством
любого множества.
Опр.5. Если число элементов множества конечное, то множество
называется конечным, в противном случае – бесконечным.
6.
Основные числовые множестваN 1; 2; ...; n; ... – множество натуральных чисел;
Z 0; 1; 2; ...; n; ... – множество целых чисел;
p
– множество рациональных чисел –
Q : p Z, q N =
q
множество конечных и периодических
десятичных дробей.
I – множество иррациональных чисел, т. е. множество
бесконечных непериодических десятичных дробей.
R – множество действительных (вещественных) чисел –
множество
периодических
(рациональных
чисел)
и
непериодических десятичных дробей (иррациональных чисел).
R Q I
N Z Q R C=
7.
Опр.6. Множество X называется счетным, если его элементыможно пронумеровать числами 1, 2, ....
Можно показать, что множества целых и рациональных чисел
являются счетными, а множество действительных чисел не
является счетным.
Ограниченные промежутки:
Отрезком [a; b] называется множество чисел, удовлетворяющих условию a ≤ x ≤ b.
Интервалом (a; b) или ]a; b[ называется множество чисел,
удовлетворяющих условию a < x < b.
Полуинтервалом (a; b] называется множество чисел,
удовлетворяющих условию a < x ≤ b.
Полуинтервалом [a; b) называется множество чисел,
удовлетворяющих условию a ≤ x < b.
Неограниченные промежутки:
; ; a; ; a; ; ; b ; ; b .
8.
Операции над множествамиОпр.7.
Объединением
(или
суммой)
множеств A и B называется множество всех
элементов, которые принадлежат хотя бы одному
из множеств A или B, и обозначается A B.
Опр.8. Пересечением (или произведением)
множеств A и B называется множество всех
элементов, которые принадлежат каждому из
множеств A и B, и обозначается A B.
Опр.9. Разностью множеств A и B
называется множество, состоящее из тех
элементов множества А, которые не принадлежат
множеству В, и обозначается A \ B .
B
А
B
А
B
А
9.
Пример 1. Для множеств X = {1, 2, 3, 0, 9} и Y = {1, 3, 4, 5, 7}найдем:
X Y = {0, 1, 2, 3, 4, 5, 7, 9}.
X Y ={1, 3}.
X \Y= {0, 2, 9}.
Опр.10. Декартовым произведением Х × Y множеств Х и Y
называется множество упорядоченных пар их элементов:
X Y x; y x X , y Y .
Аналогично определяется декартово произведение любого
конечного числа множеств:
X1
X n x1; ; xn xi X i , i 1,
, n .
R R R 2 – числовая плоскость;
R R R R 3 – трехмерное пространство;
n 1
n
R R R – n-мерное числовое (евклидово) пространство
Например,
– множество упорядоченных n-нок действительных чисел.
10.
Понятия –∞, +∞ и ∞ вводим как формальные символы.Символически записывается:
1. –∞ < x < +∞;
2. x ( ) ;
3.
x
0;
4.
, если 0 x ,
x ( )
для x 0, x R.
, если x 0,
11.
Логическая символикаСимвол или x называется квантором общности и означает:
«для всех х», «для любого х», «для каждого х», «каково бы ни
было х». Например, запись x 0 читается так: «для любого
положительного числа х».
Символ или x называется квантором существования и
означает: «существует такое х, что …», или «для некоторых х»,
или «по крайней мере для одного х», или «можно найти такое
х, что…». Например, запись x 0 читается так: «существует
такое положительное число х, что…».
Символ означает следствие. Так, если А и В – какие-то
утверждения, то запись A B означает, что из А следует В,
или если имеет место А, то имеет место В.
Символ означает равносильность. Запись A B означает,
что из А следует В и, наоборот, из В следует А или А верно тогда
и только тогда, когда и В верно.
12.
§ 2. Функция одной переменной.Основные понятия
Пусть X, Y – числовые множества.
Опр.1. Если каждому элементу x∊X по определенному
правилу f поставлен в соответствие единственный элемент y∊Y,
то говорят, что на множестве X задана функция y = f (x) со
значениями во множестве Y; обозначается
f : X Y , или y = f (x), x X .
Элемент x называется независимой переменной (или
аргументом), а y – зависимой переменной (или функцией).
Множество X называют областью определения функции,
множество E { y Y | y f ( x), x X } – областью значений функции.
Если функция задается только зависимостью y = f (x), то под ее
множеством определения понимают естественную область
определения Xf, т. е. множество всех тех действительных x, для
которых выражение f (x) имеет смысл.
13.
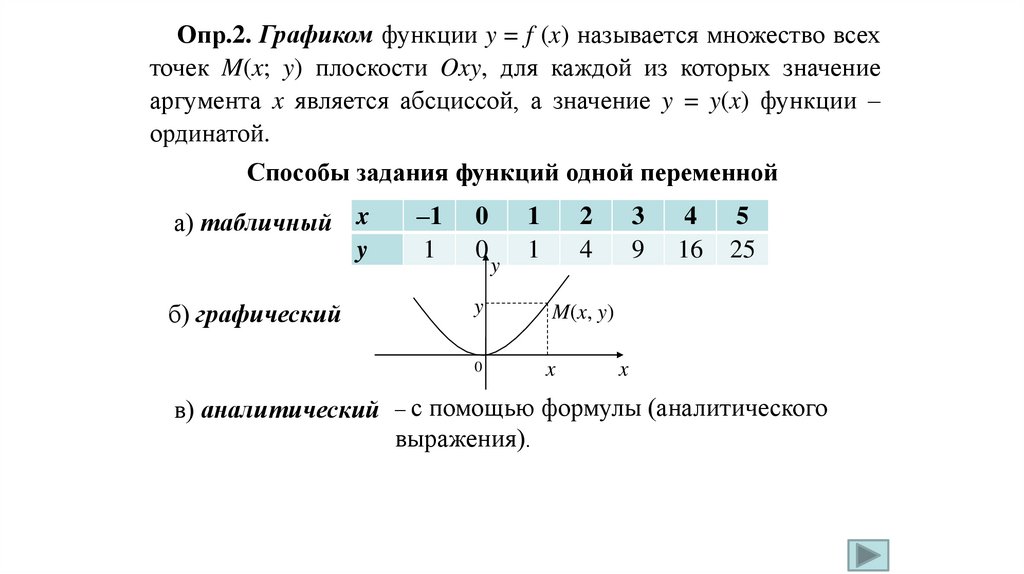
Опр.2. Графиком функции y = f (x) называется множество всехточек M(x; y) плоскости Oxy, для каждой из которых значение
аргумента x является абсциссой, а значение y = y(x) функции –
ординатой.
Способы задания функций одной переменной
а) табличный x
y
б) графический
–1
1
0
0
y
1
1
2
4
y
M(x, y)
0
x
3
9
4
16
5
25
x
в) аналитический – с помощью формулы (аналитического
выражения).
14.
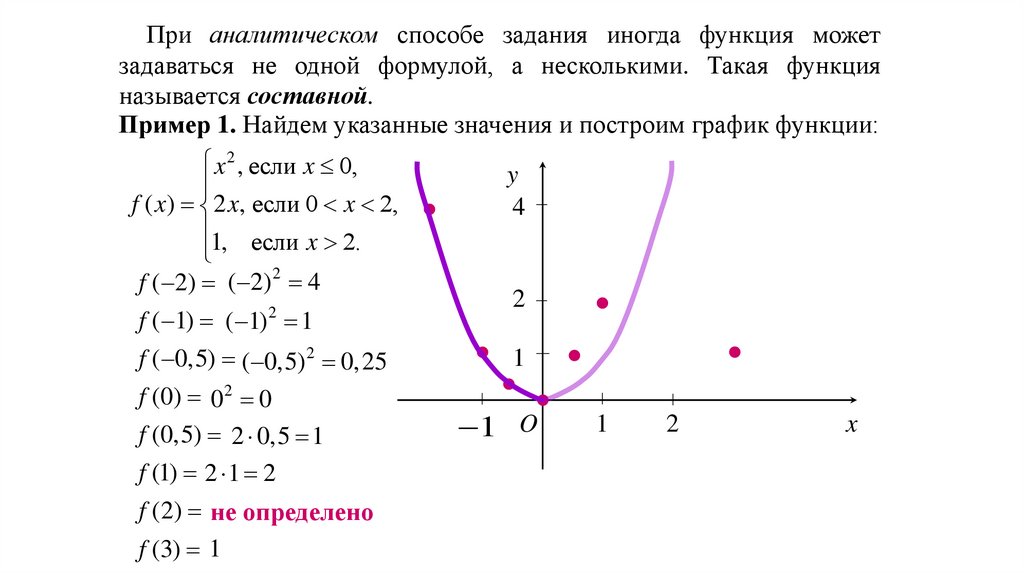
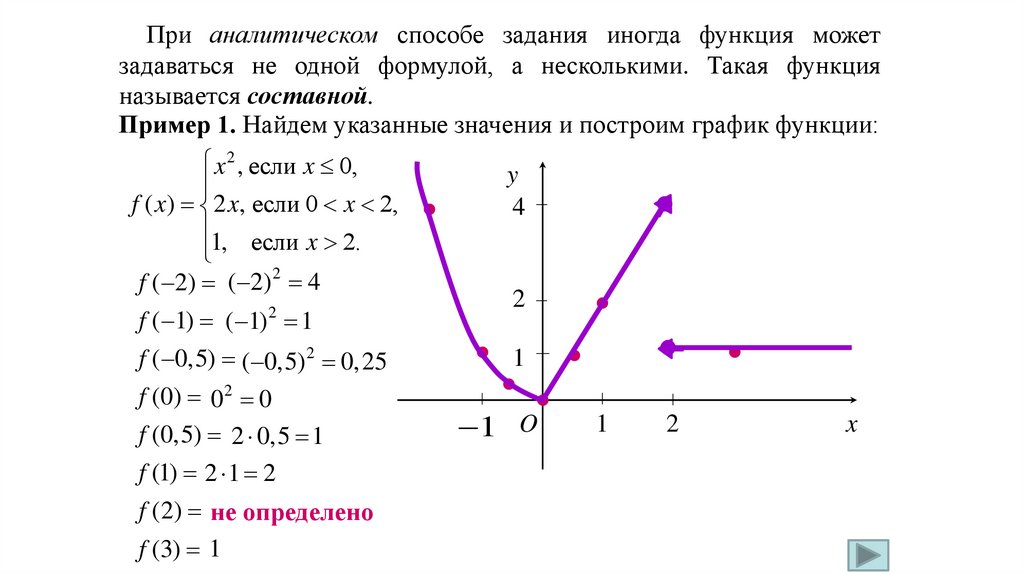
При аналитическом способе задания иногда функция можетзадаваться не одной формулой, а несколькими. Такая функция
называется составной.
Пример 1. Найдем указанные значения и построим график функции:
x 2 , если x 0,
f ( x) 2 x, если 0 x 2,
1, если x 2.
f ( 2) ( 2) 2 4
f ( 1) ( 1) 2 1
f ( 0,5) ( 0,5) 2 0, 25
f (0) 02 0
f (0,5) 2 0,5 1
f (1) 2 1 2
f (2) не определено
f (3) 1
y
4
2
1
1 O
1
2
x
15.
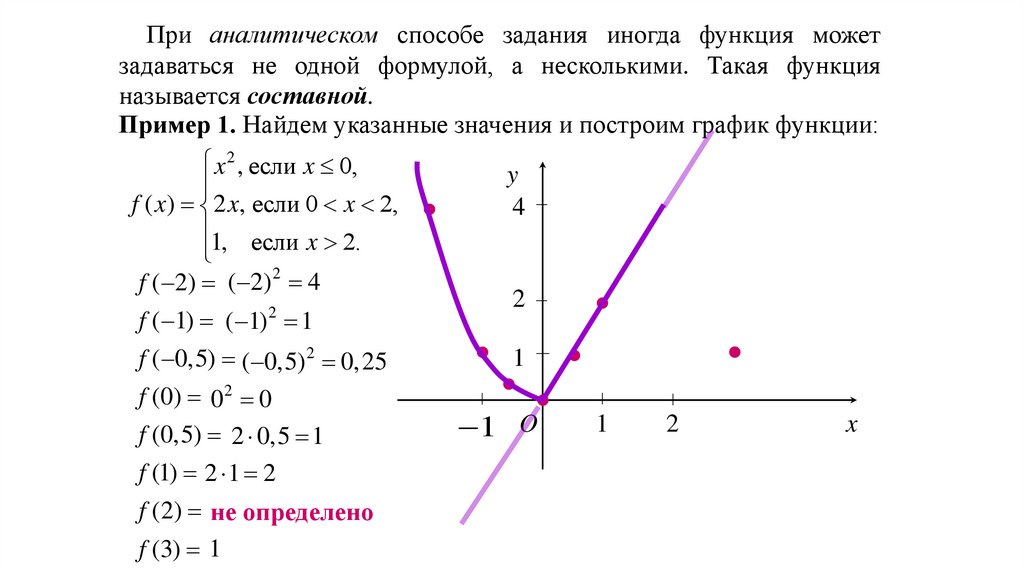
При аналитическом способе задания иногда функция можетзадаваться не одной формулой, а несколькими. Такая функция
называется составной.
Пример 1. Найдем указанные значения и построим график функции:
x 2 , если x 0,
f ( x) 2 x, если 0 x 2,
1, если x 2.
f ( 2) ( 2) 2 4
f ( 1) ( 1) 2 1
f ( 0,5) ( 0,5) 2 0, 25
f (0) 02 0
f (0,5) 2 0,5 1
f (1) 2 1 2
f (2) не определено
f (3) 1
y
4
2
1
1 O
1
2
x
16.
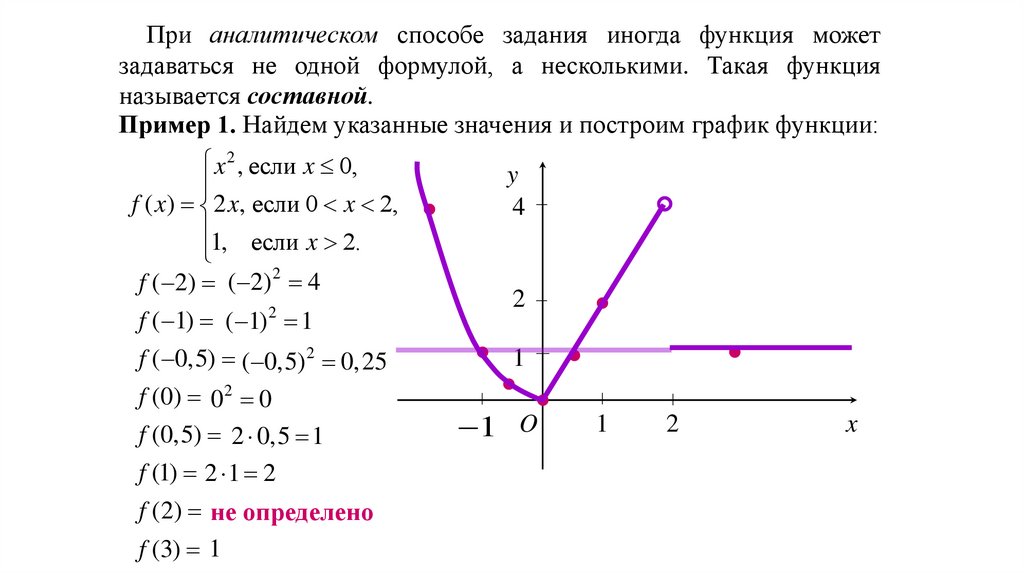
При аналитическом способе задания иногда функция можетзадаваться не одной формулой, а несколькими. Такая функция
называется составной.
Пример 1. Найдем указанные значения и построим график функции:
x 2 , если x 0,
f ( x) 2 x, если 0 x 2,
1, если x 2.
f ( 2) ( 2) 2 4
f ( 1) ( 1) 2 1
f ( 0,5) ( 0,5) 2 0, 25
f (0) 02 0
f (0,5) 2 0,5 1
f (1) 2 1 2
f (2) не определено
f (3) 1
y
4
2
1
1 O
1
2
x
17.
При аналитическом способе задания иногда функция можетзадаваться не одной формулой, а несколькими. Такая функция
называется составной.
Пример 1. Найдем указанные значения и построим график функции:
x 2 , если x 0,
f ( x) 2 x, если 0 x 2,
1, если x 2.
f ( 2) ( 2) 2 4
f ( 1) ( 1) 2 1
f ( 0,5) ( 0,5) 2 0, 25
f (0) 02 0
f (0,5) 2 0,5 1
f (1) 2 1 2
f (2) не определено
f (3) 1
y
4
2
1
1 O
1
2
x
18.
Пример 2. Функция сигнум (или функция знака)1, если x 0,
sgn x 0, если x 0,
1,если x 0.
Опр.3. Если функция задана формулой y = f (x), в которой правая
часть не содержит зависимую переменную, то говорят, что
функция задана явно.
Составная функция также задана явно.
Опр.4. Говорят, что функция y аргумента x задана неявно, если
зависимость определяется уравнением F(x; y) = 0, не разрешенным
относительно y.
Например, уравнение x 2 y 2 1 задает неявно две функции:
y 1 x2 и y 1 x2 .
От явного задания функции y = f (x) всегда можно перейти к
неявному: y - f (x) = 0. Переход от неявного задания функции к
явному не всегда возможен.
19.
К аналитическому способу задания функции относитсятакже параметрический способ задания функции, когда
переменные x и y задаются как функции некоторого
вспомогательного аргумента t, который в этом случае называется
параметром: x x t ,
y y t .
Например, в механике при задании траектории движения
координаты движущейся точки рассматриваются как функции
времени.
В некоторых случаях параметр t можно исключить и получить
явную зависимость y = y(x) как функцию x или x = x(y) как
функцию y.
20.
Пример 3. Построим линию0 t 2
t
x a cos t ,
y a sin t.
0 t
t
x
y
π/6
0
π/4
π/3
a 2
a 3
a 0,87a
0,5a
0,71a
2
2
a 2
a 3
0 0,5a 0,71а
0,87a
2
2
π/2 2π/3 3π/4 5π/6
a 2
a 3
a
0 0,5a -0,71a
-0,87a
2
2
a 3
a 2
0
0,5a
0,71а
a 0,87a
2
2
y
a
x 2 y 2 a 2 cos 2 t a 2 sin 2 t
2
2
2
2
a (cos t sin t ) a
x2 y 2 a2
π
-a
Окружность радиуса a
с центром в начале координат
O
-a
a
x
21.
Пример 4. Построим линию x a cos3 t , Астроида – траектория точки,лежащей на окружности радиуса а/4,
3
катится по внутренней
y a sin t. которая
стороне окружности радиуса а.
0 t 2
t
0 t
t
x
0
π/6
π/4
π/3
a 0,65a 0,35a 0,125a
0 0,125a 0,35a 0,65a
y
π/2 2π/3 3π/4 5π/6
0 0,125a 0,35a 0,65a a
a 0,65a 0,35a 0,125a 0
y
a
cos 2 t sin 2 t 1
x
a
23
y
a
π
23
1
x2 3 y 2 3 a2 3
-a
O
-a
a
x
22.
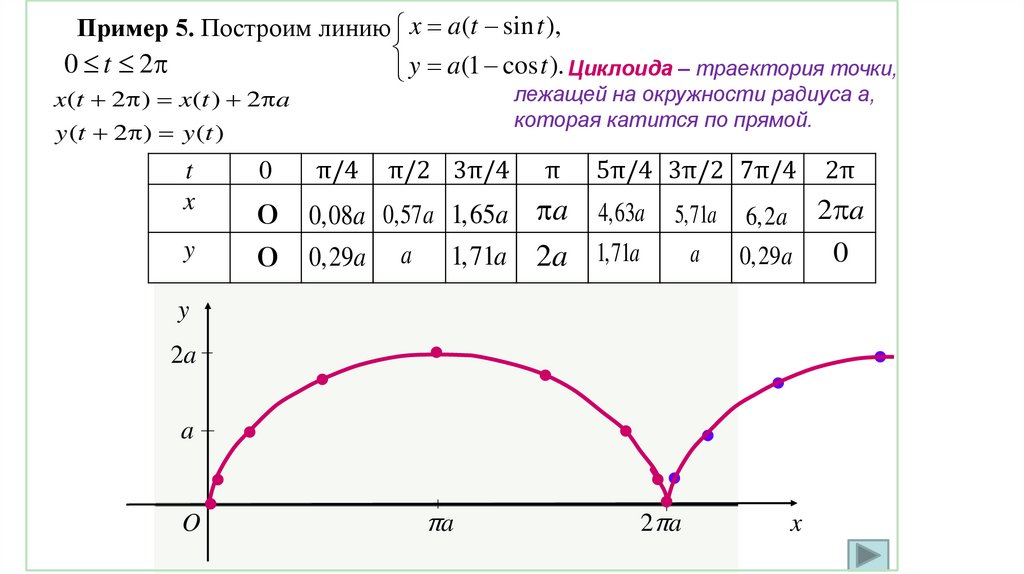
Пример 5. Построим линию x a (t sin t ),0 t 2
y a (1 cos t ). Циклоида – траектория точки,
лежащей на окружности радиуса а,
которая катится по прямой.
x (t 2 ) x(t ) 2 a
y (t 2 ) y (t )
t
x
y
0
π/4
π/2 3π/4
π
0
0
0,08a 0,57a 1,65a a
0,29a a 1,71a 2a
5π/4 3π/2 7π/4
4,63a
1,71a
5,71a 6,2a 2 a
a
0
0,29a
y
2a
a
O
πa
2π
2πa
x
23.
Основные характеристики поведения функций1. Четность и нечетность.
Опр. 5. Пусть область определения X функции y = f (x) симметрична
относительно начала координат. Если при этом
если же
f x f x , x X ,
то функция называется четной,
f x f x , x X ,
то функция называется нечетной.
⇒график четной функции симметричен относительно оси ординат,
а нечетной – относительно начала координат.
y
Например,
y
3
2) y x , x R
1) y = x2, x R
является четной.
0 1 x
является нечетной.
x
0
2
3) y x 2 x 2, x R не является ни четной, ни нечетной, т.к.
y x x 2 2 x 2,
2
y x x 2 x 2 x2 2x 2
2
y
x
x
2x 2 .
Такая функция называется функцией общего вида.
24.
2. Периодичность.Опр. 6. Функция y = f (x) называется периодической, если для нее
существует такое число T > 0, что при любых x из области
определения функции числа x + T и x – T также принадлежат этой
области и выполняется равенство
f (x – T) = f (x) = f (x + T).
Наименьшее из чисел Т > 0 (если оно существует) называется
наименьшим периодом функции.
25.
3. Монотонность.Опр. 7. Функция y = f (x) называется возрастающей (убывающей) на
некотором множестве A X , если большему значению аргумента из
множества A соответствует большее (меньшее) значение функции y = f (x),
т. е. x1 , x2 A из того, что x1 < x2 следует f (x1) < f (x2) (f (x1) > f (x2)).
y
x1
y
x1
x2
x
f (x2)
x2
x
f (x1)
f (x2)
f (x1)
Если в определении возрастающей (убывающей) функции неравенства
нестрогие f (x1) ≤ f (x2) (f (x1) ≥ f (x2)), то функция называется неубывающей
(соответственно, невозрастающей).
Возрастающие, убывающие, невозрастающие, неубывающие функции
называются монотонными.
26.
4. Ограниченность функции.Опр. 8. Функция y = f (x) называется ограниченной сверху (снизу) на
множестве A X , если существует такое число M (m), что для любых
x из этого множества выполняется условие
f (x) < M (f (x) > m).
Функция y = f (x) называется ограниченной на множестве A X ,
если существует такое положительное число M, что
f x M , x A.
Например,
1) функция y = x2
ограничена снизу на всей числовой оси и
неограничена сверху;
2) функция y = sin x
ограничена на множестве R;
3) функция y = x
неограничена на множестве R.
27.
Сложная функцияОпр.9. Пусть функция u ( x) : X U ;
y f (u ) : U Y .
Тогда функция
y = f (φ(x)), называемая сложной функцией (или
суперпозицией (композицией) функций φ и f, или функцией от
функции), определена на множестве X и отображает его в множество Y.
При этом y называют промежуточным аргументом (переменной),
а x – независимой переменной.
Например, функцию y = sin 2x можно рассматривать как сложную,
образованную суперпозицией функций u = 2x и y = sin u.
28.
Обратная функцияОпр.10. Пусть функция y = f (x) задает взаимно однозначное
соответствие между множеством определения X и множеством значений Y,
т. е. каждому числу x∊X соответствует единственное число y∊Y, и наоборот.
Если мы рассмотрим обратное отображение множества Y на множество X,
при котором каждому y∊Y будем ставить в соответствие единственное
число x∊X такое, что y = f (x), то получим функцию x = φ(y), которая
называется обратной по отношению к данной функции y = f (x), и
обозначается x = f –1(y).
Поскольку обычно аргумент обозначают x, а зависимую переменную y, то
говорят, что функция y = φ(x) является обратной к функции y = f (x) на
множестве X, если f(φ(x)) = x при всех x∊X .
y
y=x
Графики функций y = f (x) и y = f –1(x)
симметричны относительно прямой y = x.
1
x
y=2
Например, функция y = 2x
имеет обратную функцию x = log2y.
y = f –1(x) = log2x.
0
1
y =log2x
x
29.
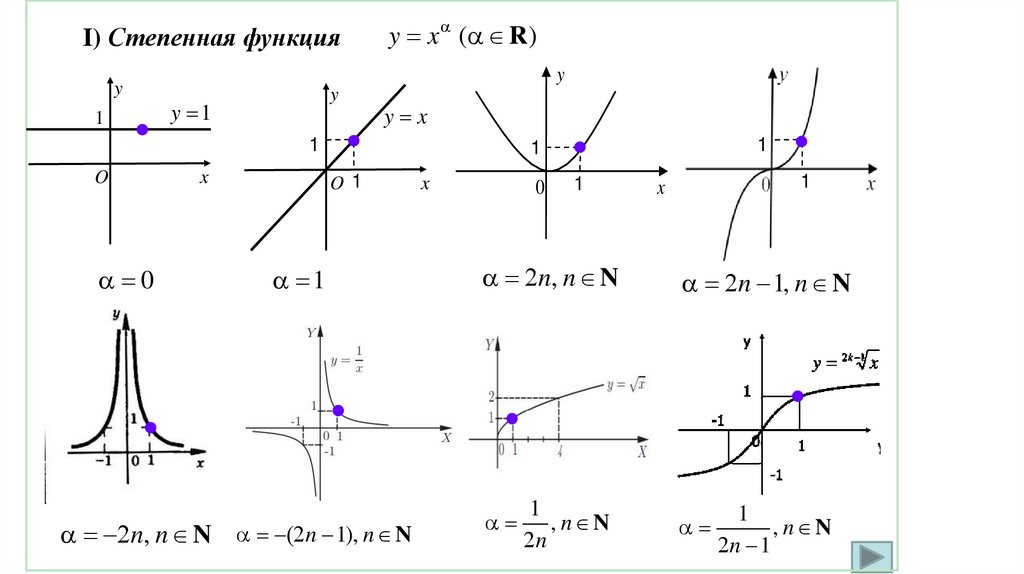
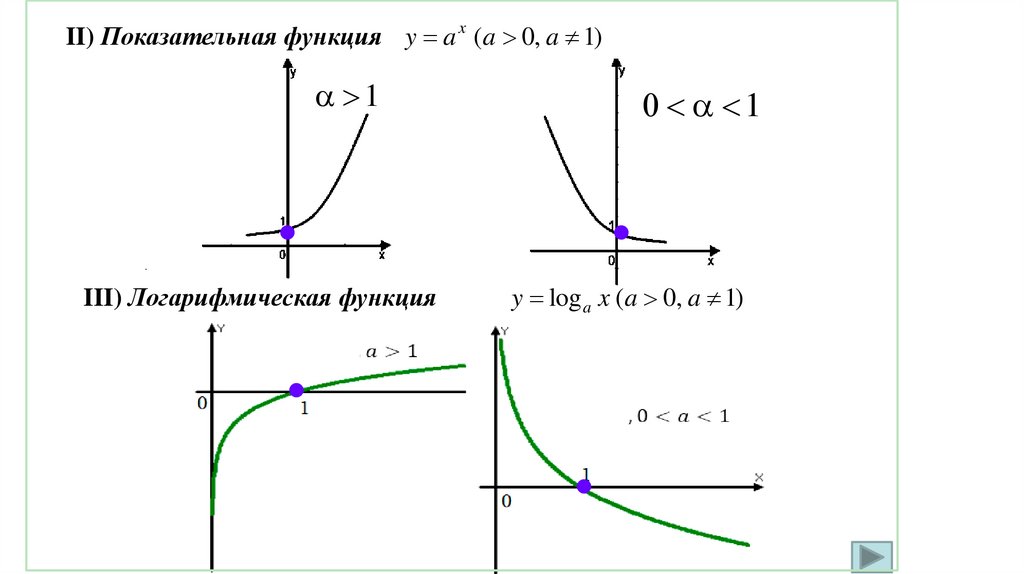
Основные элементарные функции и их графикиОпр.11. К основным элементарным функциям относятся:
y
x
( R )
I) степенная функция
II) показательная функция
y a x (a 0, a 1)
III) логарифмическая функция
y log a x (a 0, a 1)
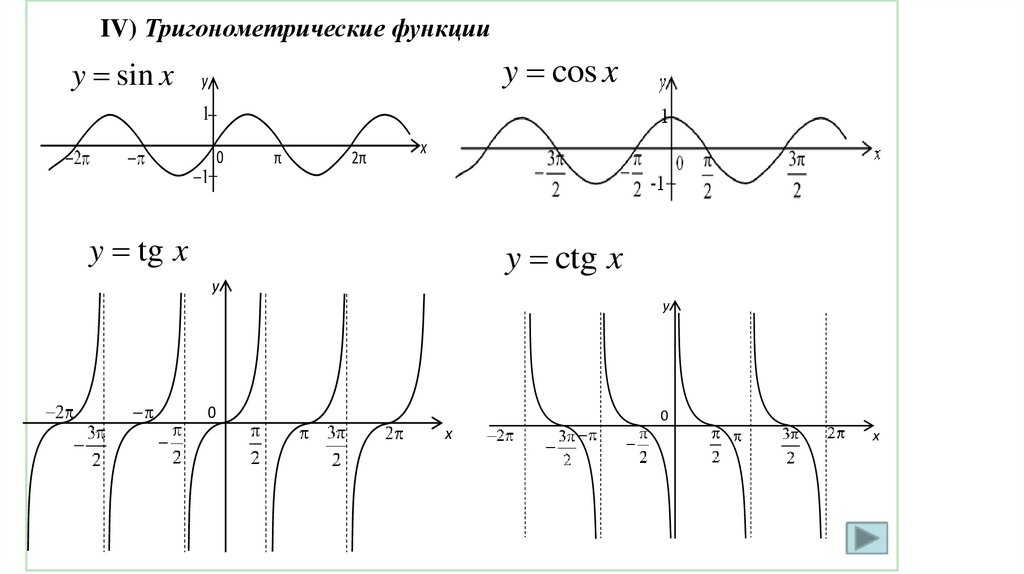
IV) тригонометрические функции
y = sin x, y = cos x, y = tg x, y = ctg x;
V) обратные тригонометрические функции
y = arcsin x, y = arccos x, y = arctg x, y = arcctg x.
30.
I) Степенная функцияy
1
y x ( R )
y
y
y 1
y x
1
O
0
x
y
1
1
O 1
1
n, n N n 1), n N
x
0
1
x
1 0
n, n N
n 1, n N
1
, n N
n
1
, n N
n 1
x
31.
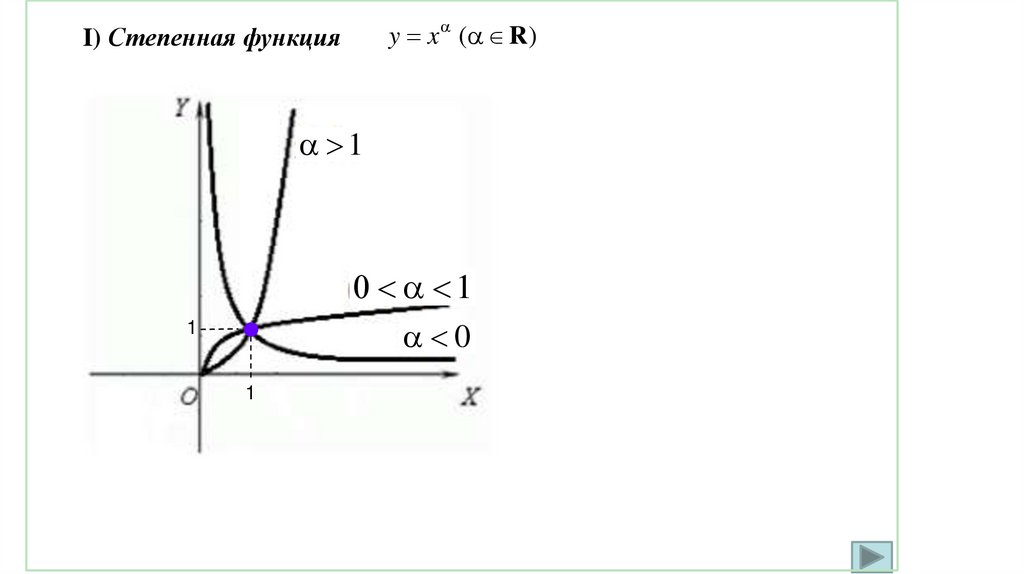
y x ( R )I) Степенная функция
1
1
0
1
1
32.
II) Показательная функция y a x (a 0, a 1)1
III) Логарифмическая функция
1
y log a x (a 0, a 1)
33.
IV) Тригонометрические функцииy sin x
y cos x
y
1
0
π
2π
x
y tg x
y ctg x
y
y
0
0
x
x
34.
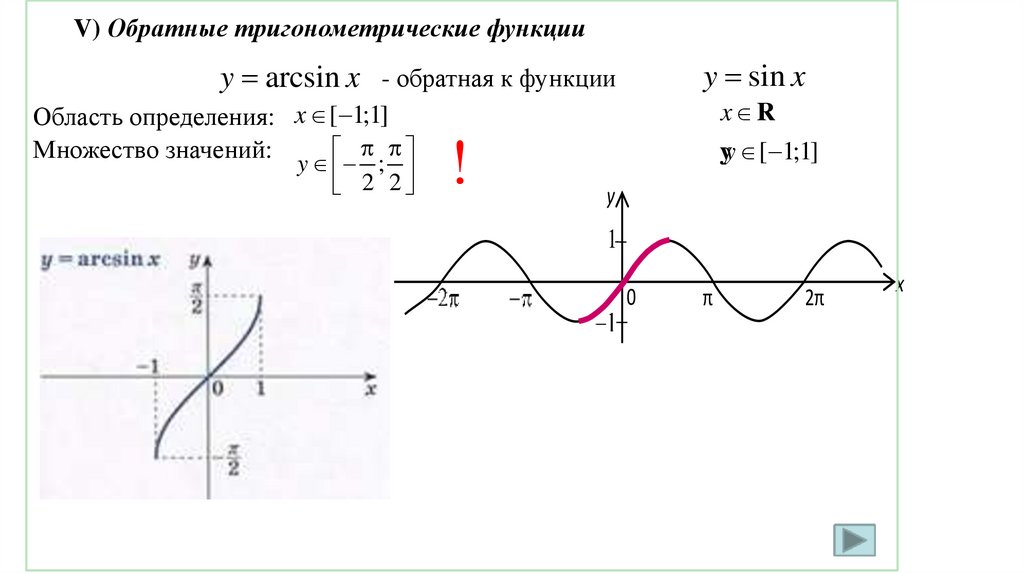
V) Обратные тригонометрические функцииy sin x
y arcsin x - обратная к функции
Область определения: x [ 1;1]
Множество значений:
y ;
2 2
!
x R
yy [ 1;1]
y
1
0
π
2π
x
35.
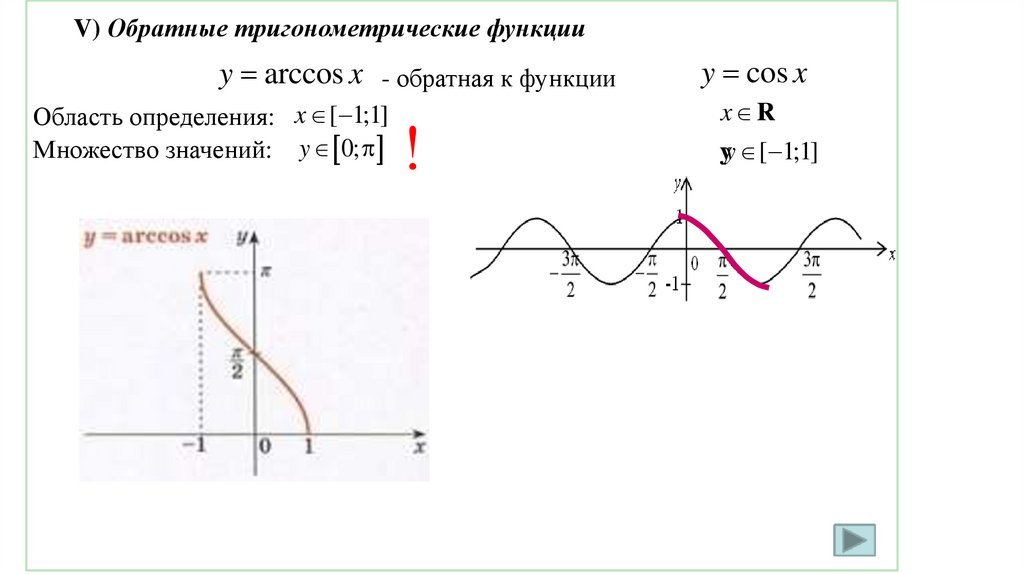
V) Обратные тригонометрические функцииy arccos x - обратная к функции
Область определения: x [ 1;1]
Множество значений: y 0;
!
y cos x
x R
yy [ 1;1]
36.
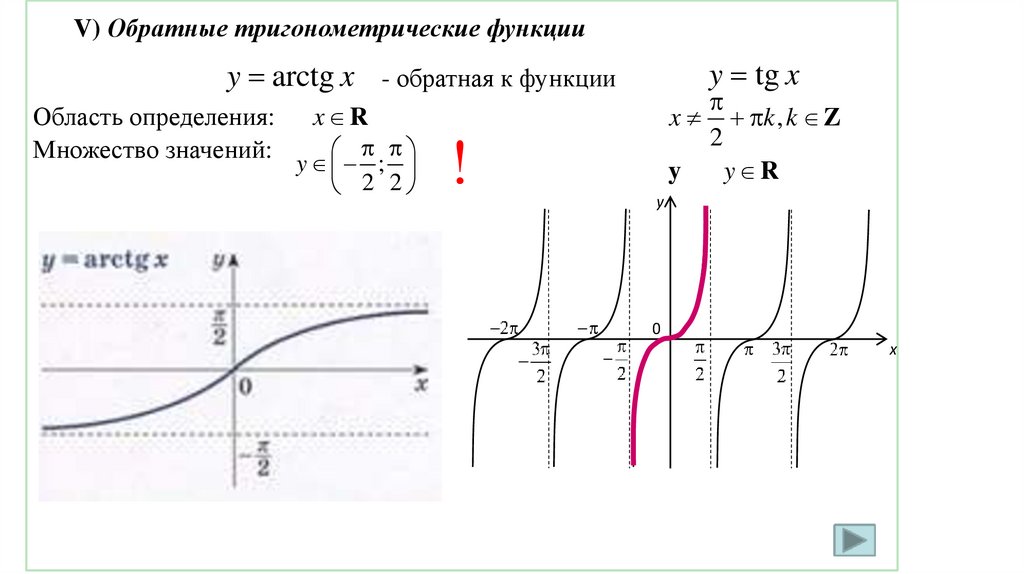
V) Обратные тригонометрические функцииy tg x
y arctg x - обратная к функции
Область определения:
Множество значений:
x R
y ;
2 2
!
x k , k Z
2
y
y R
y
0
x
37.
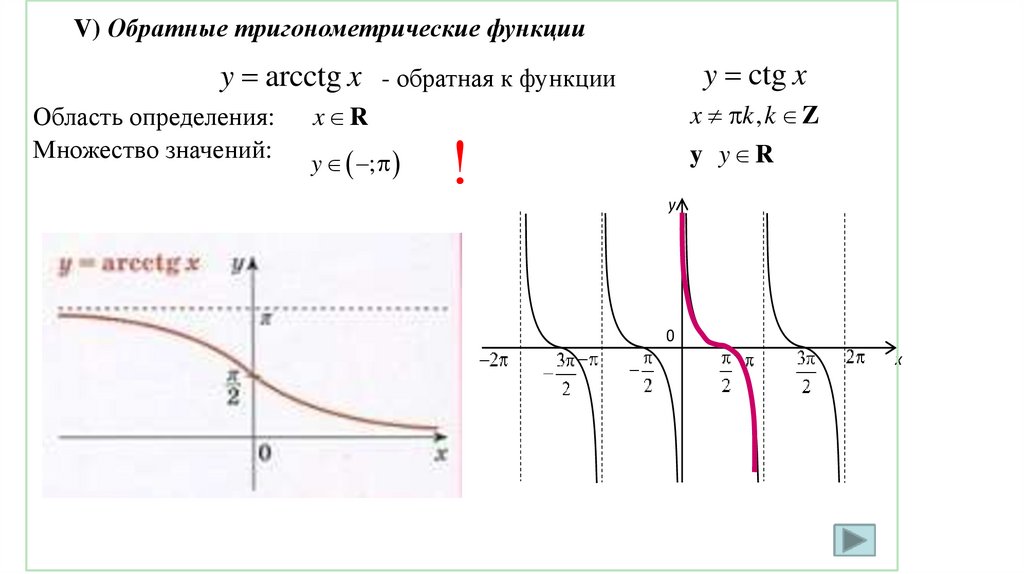
V) Обратные тригонометрические функцииy ctg x
y arcctg x - обратная к функции
Область определения:
Множество значений:
x k , k Z
y y R
x R
y ;
!
y
0
x
38.
V) Обратные тригонометрические функцииarccos( x) arccos x
arcctg( x) arcctg x
arcsin x arccos x
2
arctg x arcctg x
2
arcsin( x) arcsin x
arctg( x) arctg x
Опр.12. Элементарными функциями называются функции, которые
можно получить из основных элементарных функций с помощью
конечного числа операций сложения, вычитания, умножения, деления и
образования сложных функций.
1, x 0,
2
Например,
y x , 0 x 2,
3
2 x2 5x
y
.
x, x 2.
sin3x
- элементарная функция
- неэлементарная функция
39.
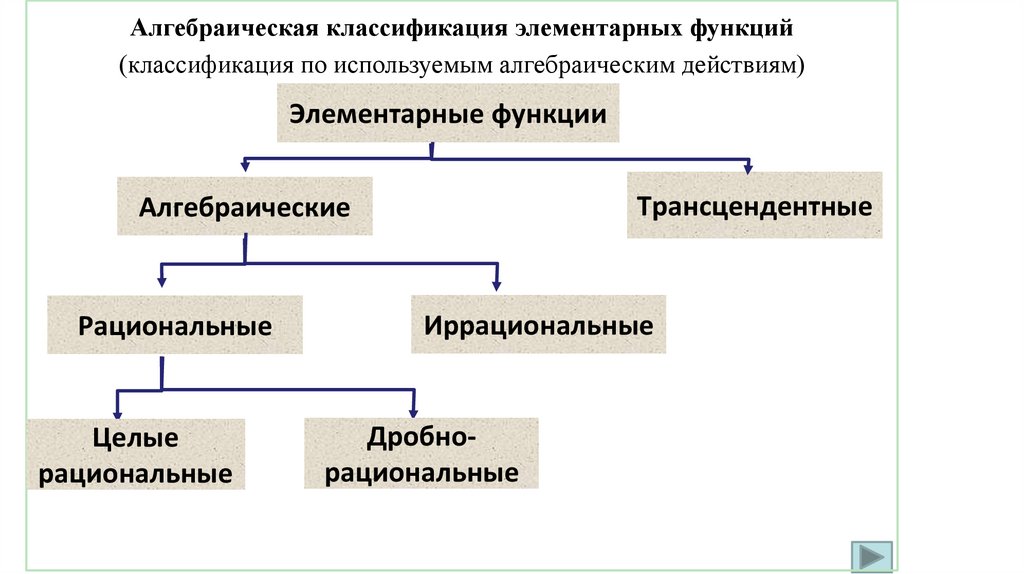
Алгебраическая классификация элементарных функций(классификация по используемым алгебраическим действиям)
Элементарные функции
Трансцендентные
Алгебраические
Рациональные
Целые
рациональные
Иррациональные
Дробнорациональные
40.
Целая рациональная функция (многочлен, полином) – это функциявида

























 mathematics
mathematics








