ЛЕКЦИЯ №3.ДИФРАКИЯ СВЕТА

1.

Лекция №22.
ДИФРАКЦИЯ СВЕТА.
1. Принцип Гюйгенса –Френеля.
2. Метод зон Френеля.
3. Дифракция Френеля на круглом отверстии и непрозрачном
диске.
4. Дифракция Фраунгофера на одной щели. Дифракционная
решетка.
5. Дифракция на кристаллической решетке. Формула Вульфа
– Брэггов.
6. Голография ( самостоятельно ).

2.

1 вопрос – Принцип Гюйгенса – Френеля.
Дифракцией света называется явление отклонения света от
прямолинейного направления распространения при
прохождении вблизи препятствий. При дифракции световые
волны огибают границы непрозрачных тел и могут проникать
в область геометрической тени.
Дифракция объясняется на
основе принципа Гюйгенса–
Френеля: световая волна,
возбуждаемая каким либо
источником S, может быть
представлена как результат
суперпозиции когерентных
вторичных вол, излучаемых
фиктивными источниками.
Рисунок 1 иллюстрирует принцип Гюйгенса–Френеля. ΔS1 и ΔS2 –
элементы волнового фронта.

3.

2 вопрос – Метод зон Френеля.
В результате интерференции вторичных волн в точке P
возникает некоторое результирующее колебание, квадрат
амплитуды которого (интенсивность) нужно определить при
заданных значениях длины волны λ, амплитуды Aо падающей
волны и геометрии задачи. Для облегчения расчета Френель
предложил разбить волновую поверхность падающей волны в
месте расположения препятствия на кольцевые зоны (зоны
Френеля) по следующему правилу: расстояние от границ
соседних зон до точки P должны отличается на полдлины
волны.

4.

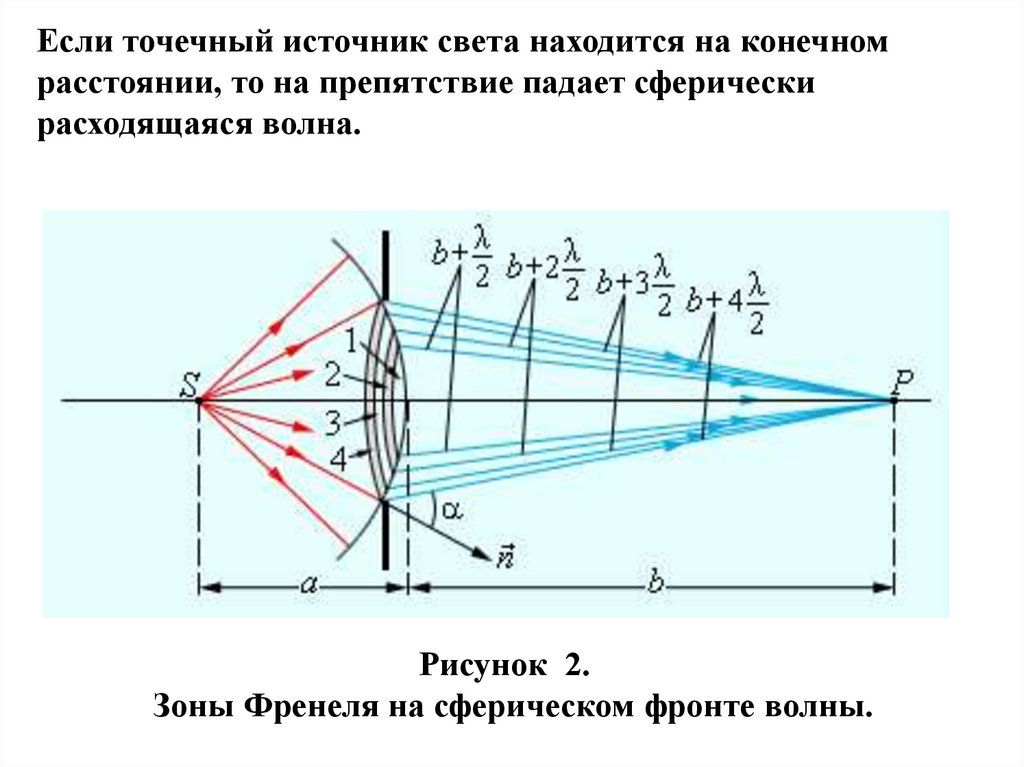
Если точечный источник света находится на конечном
расстоянии, то на препятствие падает сферически
расходящаяся волна.
Рисунок 2.
Зоны Френеля на сферическом фронте волны.

5.

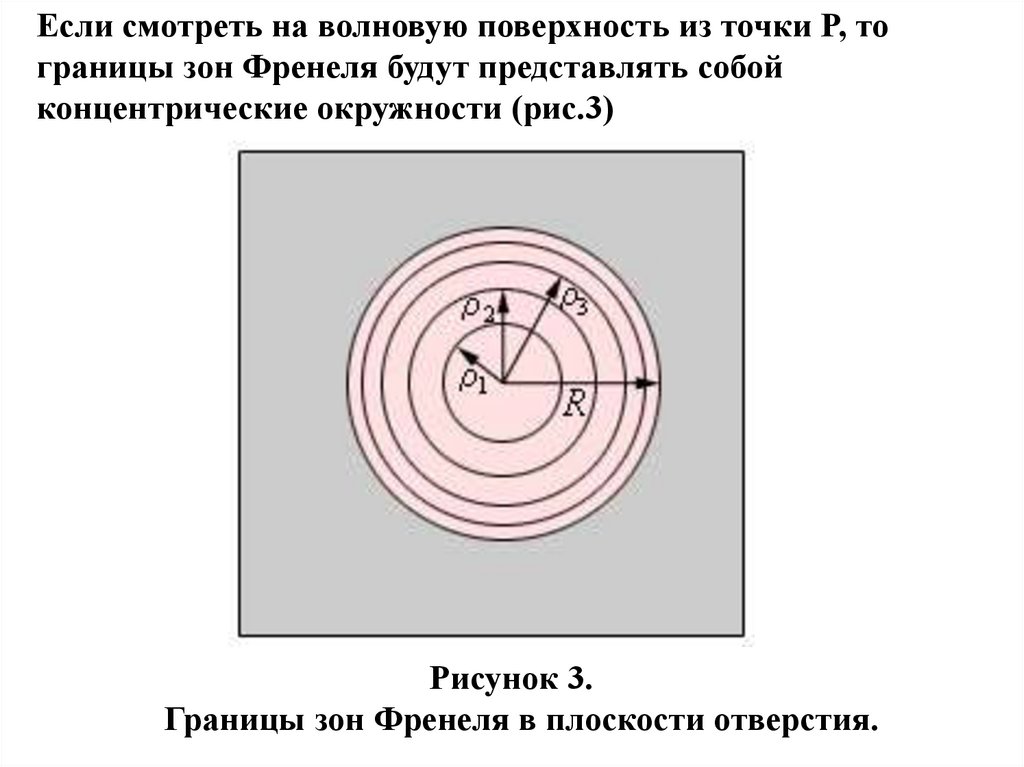
Если смотреть на волновую поверхность из точки P, то
границы зон Френеля будут представлять собой
концентрические окружности (рис.3)
Рисунок 3.
Границы зон Френеля в плоскости отверстия.

6.

С хорошим приближением можно считать, что амплитуда
колебаний, вызываемых некоторой зоной, равна среднему
арифметическому из амплитуд колебаний, вызываемых
двумя соседними зонами, т. е.
Так как расстояния от двух соседних зон до точки наблюдения
отличаются на λ / 2, возбуждаемые этими зонами колебания
находится в противофазе. Поэтому волны от любых двух
соседних зон почти гасят друг друга. Суммарная амплитуда в
точке наблюдения есть
А А1 А2 А3 А4 ... А1 ( А2 А3 ) ( А4 А5 ) ... А1
Если открыты все зоны Френеля, то до точки наблюдения
дойдет невозмущенная препятствием волна с амплитудой Aо:

7.

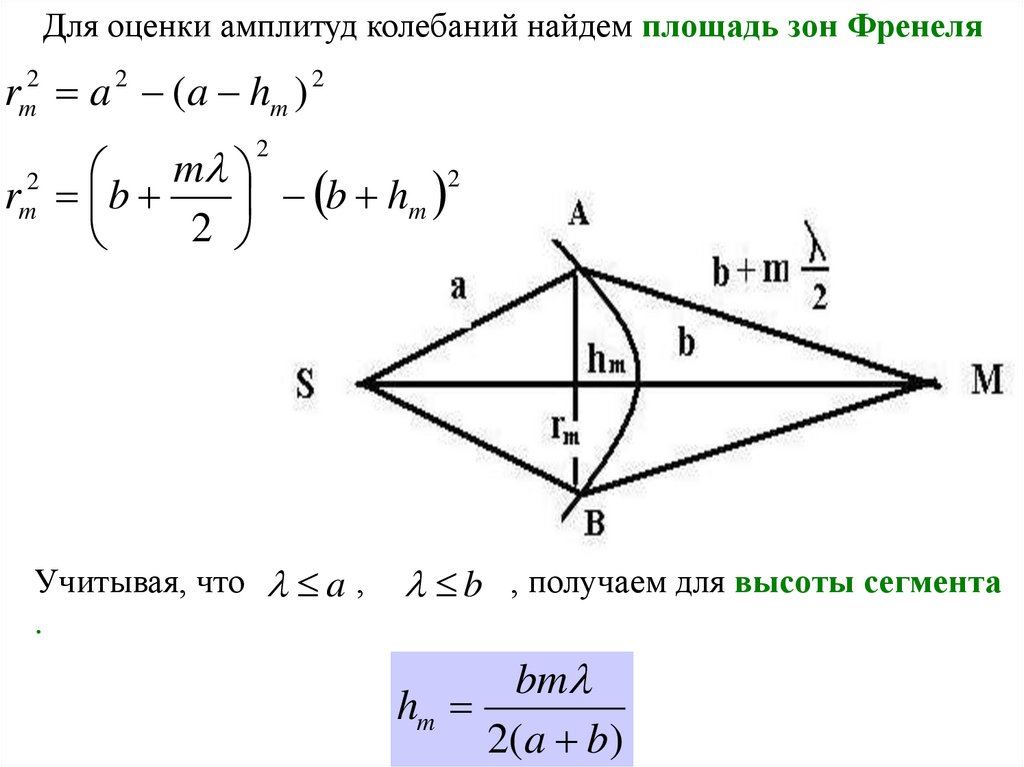
Для оценки амплитуд колебаний найдем площадь зон Френеля
rm2 a 2 (a hm ) 2
m
2
r b
b hm
2
2
2
m
Учитывая, что a ,
.
b , получаем для высоты сегмента
bm
hm
2(a b)

8.

Площадь сферического сегмента
S m 2 ahm
ab
m
a b
Площадь m-ой зоны Френеля
ab
S
a b
Площадь зон Френеля не зависит от номера зоны,
следовательно, площади зон Френеля одинаковы.
Радиус внешней границы m-зоны Френеля
rm
ab
m
a b
Оценим размеры зон Френеля. Пусть, например, дифракционная
картина наблюдается на экране, расположенном на расстоянии
L = 1 м от препятствия. Длина волны света λ = 600 нм (красный
свет). Тогда радиус первой зоны Френеля равен 0,77мм.

9.

Дифракционные явления проявляются наиболее отчетливо,
когда на препятствии укладывается лишь небольшое число зон.
Если число зон Френеля, укладывающихся на препятствии,
становится очень большим, дифракционные явления
практически незаметны.
Геометрическая оптика является предельным случаем
волновой оптики.
Модель:
Зоны Френеля.

10.

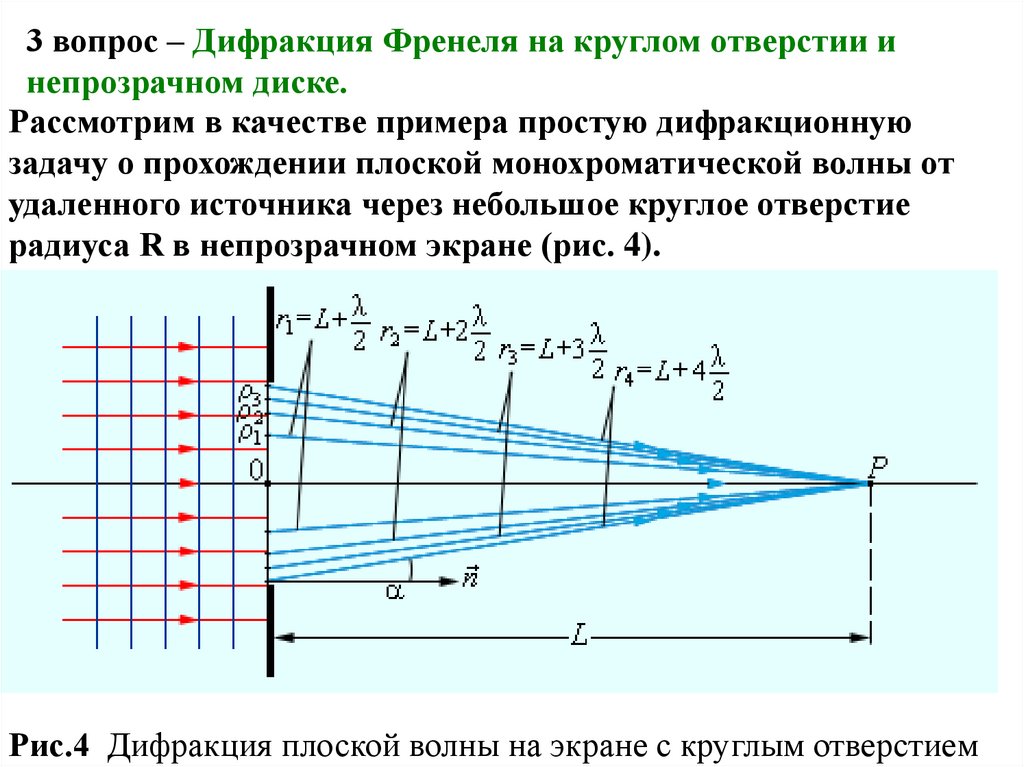
3 вопрос – Дифракция Френеля на круглом отверстии и
непрозрачном диске.
Рассмотрим в качестве примера простую дифракционную
задачу о прохождении плоской монохроматической волны от
удаленного источника через небольшое круглое отверстие
радиуса R в непрозрачном экране (рис. 4).
Рис.4 Дифракция плоской волны на экране с круглым отверстием

11.

а). Дифракция на круглом отверстии
. Если отверстие в непрозрачном экране оставляет открытой
только одну зону Френеля, то амплитуда колебаний в точке
наблюдения возрастает в 2 раза (а интенсивность в 4 раза) по
сравнению с действием невозмущенной волны. Если открыть
две зоны, то амплитуда колебаний обращается в нуль. Если
изготовить непрозрачный экран, который оставлял бы
открытыми только несколько нечетных (или только несколько
четных) зон, то амплитуда колебаний резко возрастает.
Например, если открыты 1, 3 и 5 зоны, то
А 6 А0 ;
I 36 I 0
Такие пластинки, обладающие свойством фокусировать свет,
называются зонными пластинками.

12.

б). Дифракция на непрозрачном диске
При дифракции света на круглом диске закрытыми оказываются
зоны Френеля первых номеров от 1 до m. Тогда амплитуда
колебаний в точке наблюдения будет равна
или A = Am + 1 / 2, так как выражения, стоящие в скобках,
равны нулю. Если диск закрывает зоны не слишком больших
номеров, то Am + 1 ≈ 2Aо и A ≈ Aо, т. е. в центре картины при
дифракции света на диске наблюдается интерференционный
максимум. Это – так называемое пятно Пуассона, оно
окружено светлыми и темными дифракционными кольцами.

13.

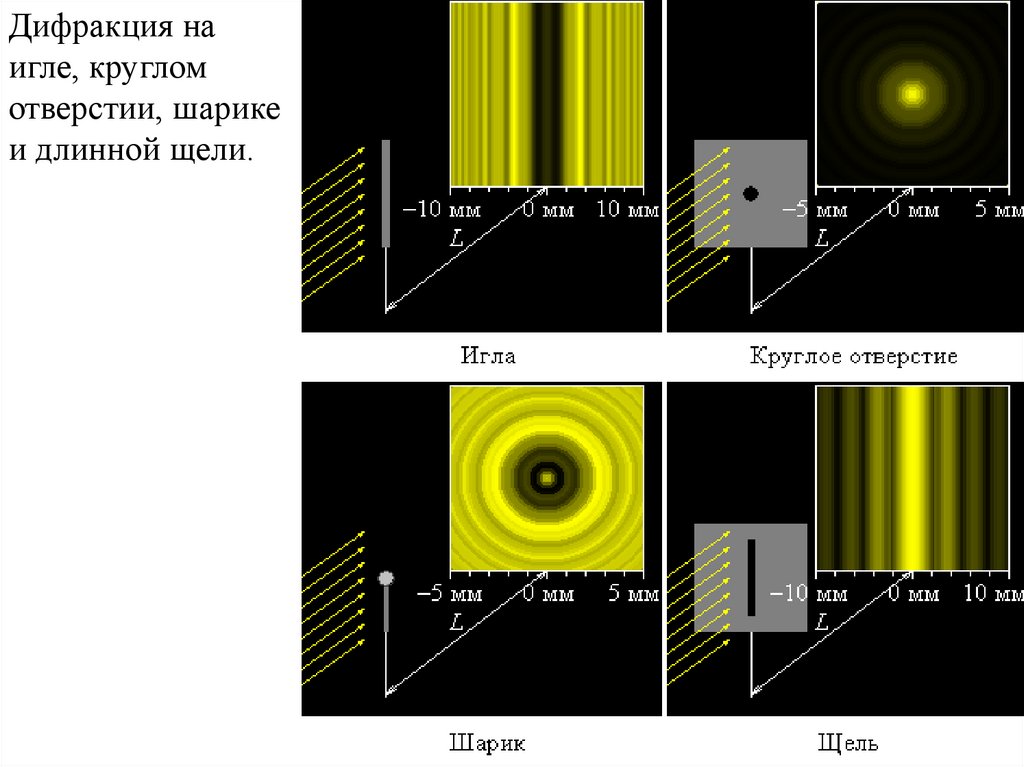
Дифракция на
игле, круглом
отверстии, шарике
и длинной щели.

14.

4 вопрос – Дифракция Фраунгофера от одной щели.
Дифракционная рещетка.
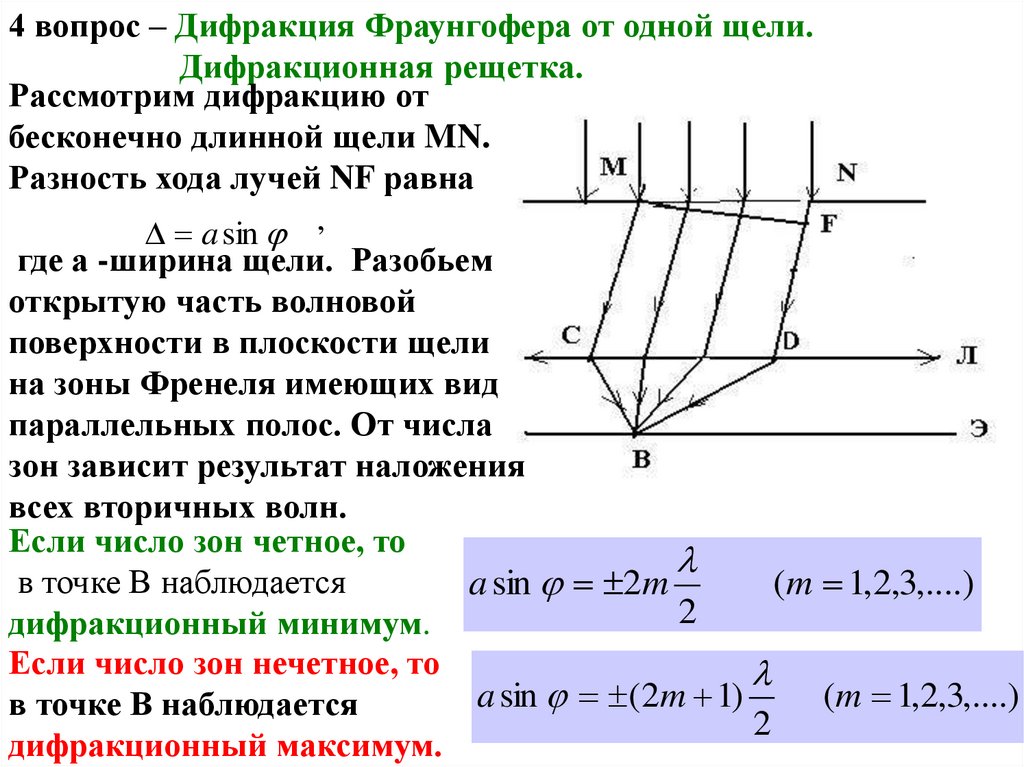
Рассмотрим дифракцию от
бесконечно длинной щели MN.
Разность хода лучей NF равна
a sin ,
где а -ширина щели. Разобьем
открытую часть волновой
поверхности в плоскости щели
на зоны Френеля имеющих вид
параллельных полос. От числа
зон зависит результат наложения
всех вторичных волн.
Если число зон четное, то
в точке В наблюдается
a sin 2m
(m 1,2,3,....)
2
дифракционный минимум.
Если число зон нечетное, то
a sin (2m 1)
(m 1,2,3,....)
в точке В наблюдается
2
дифракционный максимум.

15.

На явлении дифракции основано устройство дифракционных
решеток. Это совокупность большого количества узких щелей,
повторяющихся через расстояние
l
d a b
d – период дифракционной решетки.
N
Дифракционные
решетки делятся на
отражательные
(штрихи нанесены
на металлическую
поверхность) и
прозрачные
(штрихи нанесены
на стеклянную
поверхность).

16.

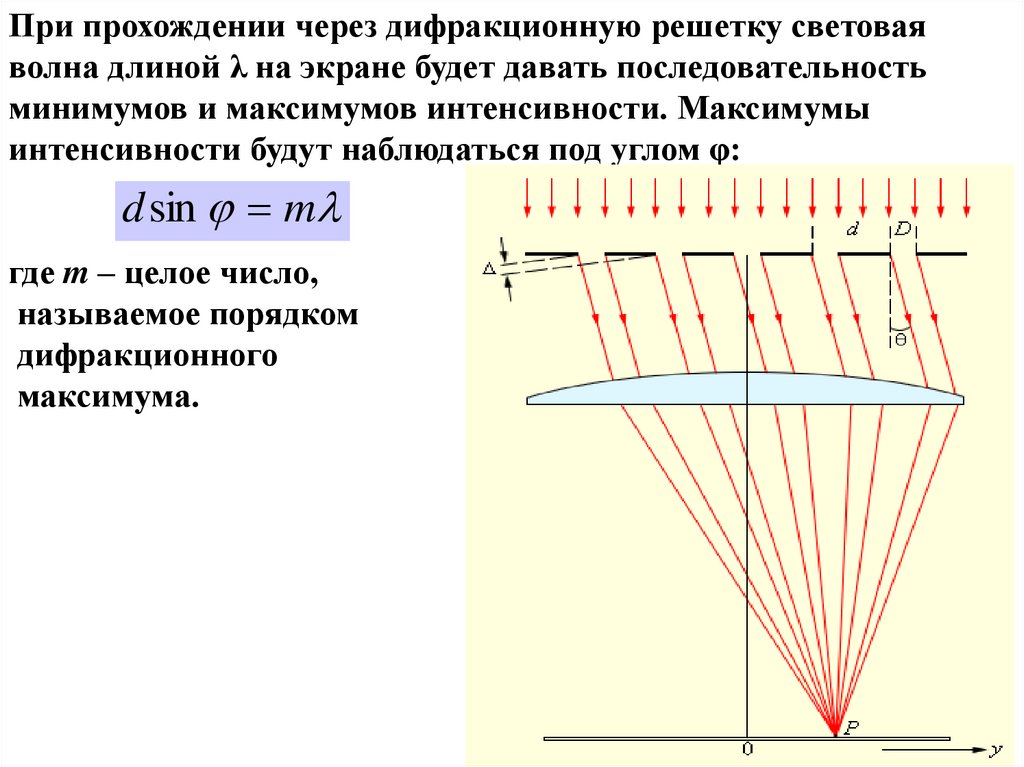
При прохождении через дифракционную решетку световая
волна длиной λ на экране будет давать последовательность
минимумов и максимумов интенсивности. Максимумы
интенсивности будут наблюдаться под углом φ:
d sin m
где m – целое число,
называемое порядком
дифракционного
максимума.

17.

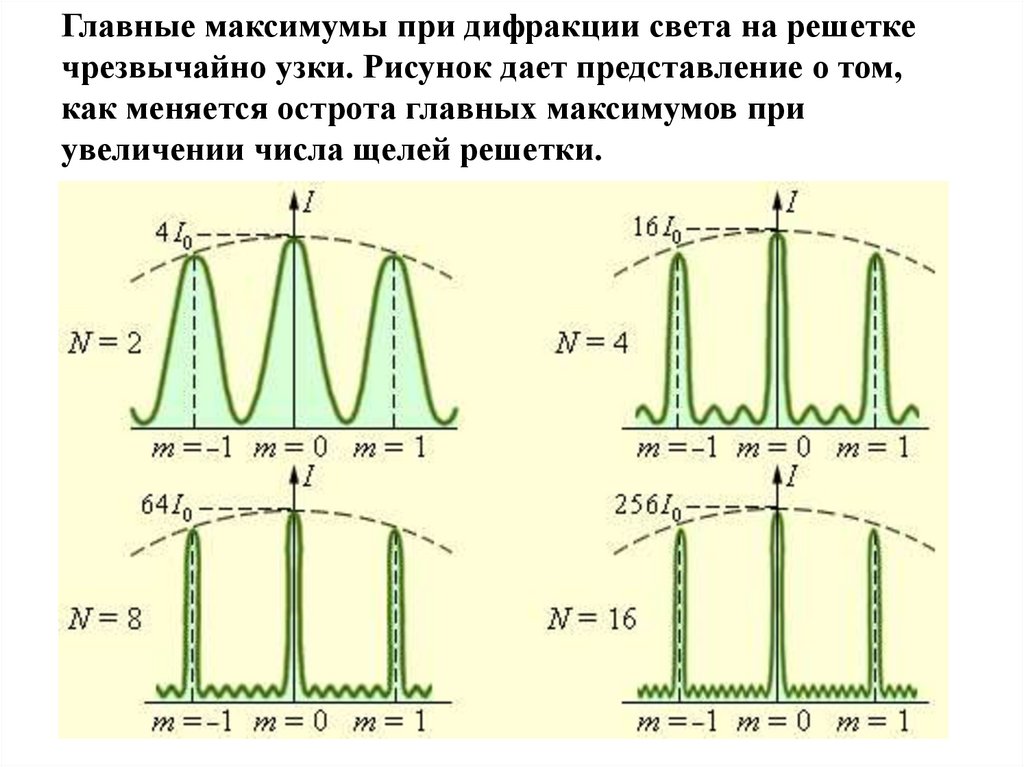
Главные максимумы при дифракции света на решетке
чрезвычайно узки. Рисунок дает представление о том,
как меняется острота главных максимумов при
увеличении числа щелей решетки.

18.

Разложение белого света в спектр при
помощи дифракционной решетки.

19.

5 вопрос – Дифракция на кристаллической решетке.
Формула Вульфа – Брэггов.
Кристаллы можно использовать в качестве
пространственных решеток для наблюдения дифракции
рентгеновского излучения, поскольку расстояние между
атомами в кристаллах одного порядка с длиной волны
рентгеновского излучения ( 10 12 10 8 м ). При разности
хода между двумя лучами, отраженными от соседних
кристаллографических плоскостей, кратной целому числу
длин волн, наблюдается дифракционный максимум
(формула Вульфа-Брэггов)
2d sin m
(m 1,2,3,...)
d - расстояние между параллельными
кристаллографическими плоскостями, угол скольжения
(угол между направлением падающих лучей и
кристаллографической плоскостью.