объем пирамиды

1.

2.

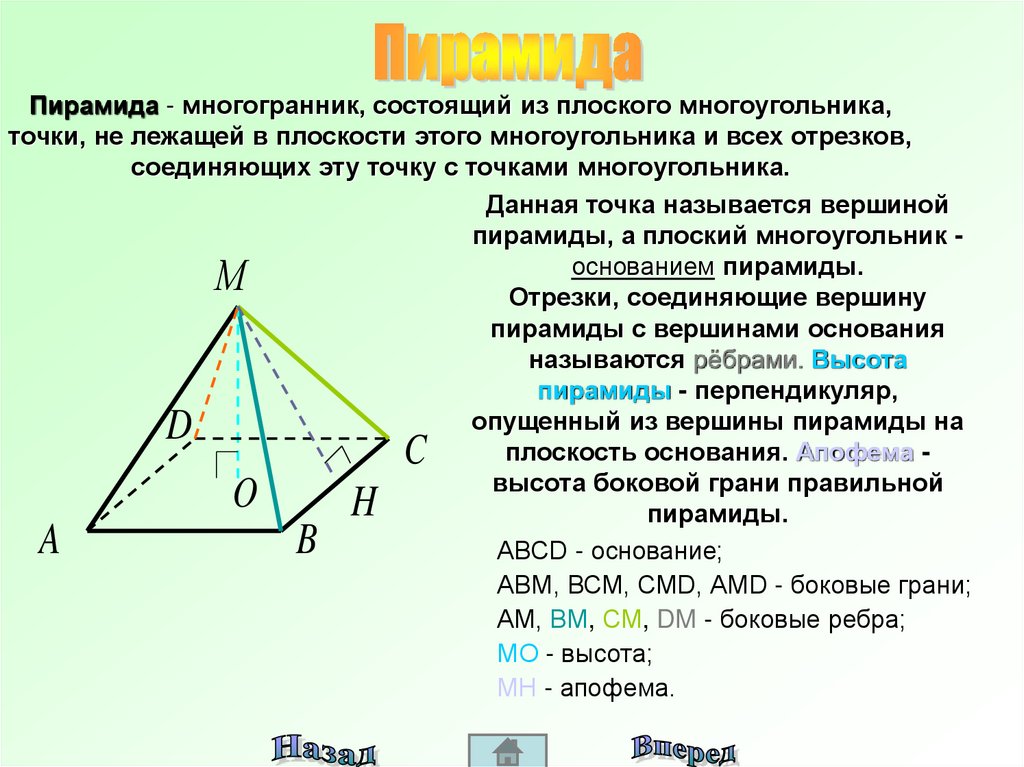
Пирамида - многогранник, состоящий из плоского многоугольника,
точки, не лежащей в плоскости этого многоугольника и всех отрезков,
соединяющих эту точку с точками многоугольника.
Данная точка называется вершиной
пирамиды, а плоский многоугольник основанием пирамиды.
Отрезки, соединяющие вершину
пирамиды с вершинами основания
называются рёбрами. Высота
пирамиды - перпендикуляр,
опущенный из вершины пирамиды на
плоскость основания. Апофема высота боковой грани правильной
пирамиды.
АВСD - основание;
АВМ, ВСМ, СМD, АМD - боковые грани;
АМ, ВМ, СМ, DM - боковые ребра;
МО - высота;
МН - апофема.
М
D
C
O
A
B
H

3.

m
m
m
m
m
m
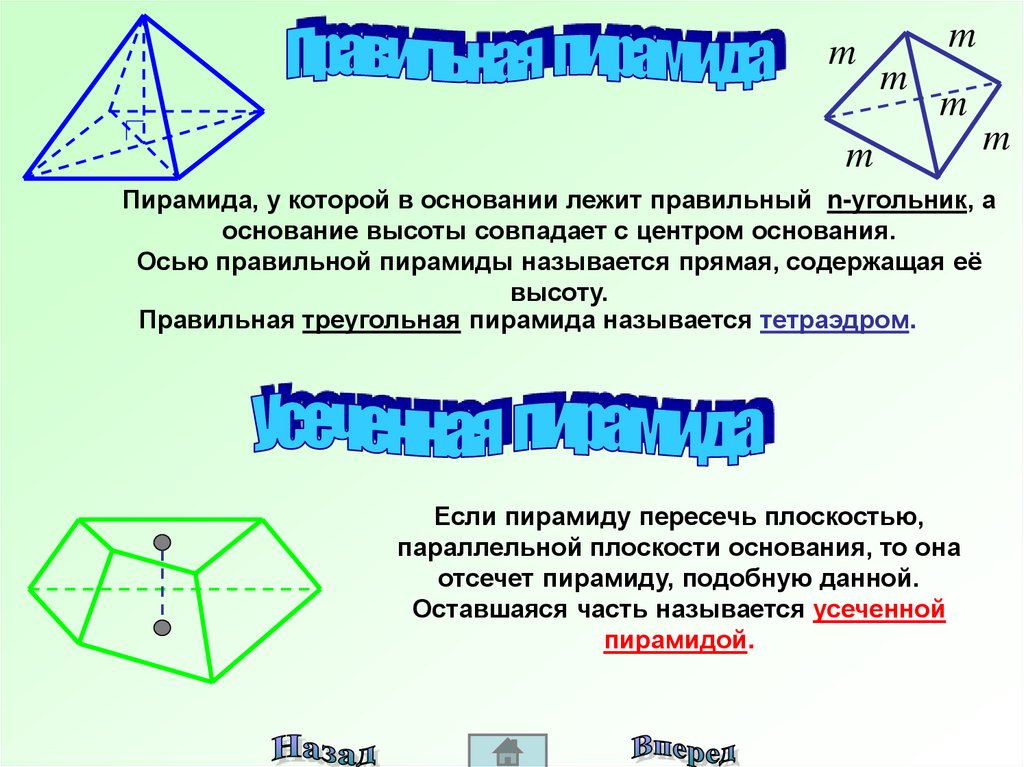
Пирамида, у которой в основании лежит правильный n-угольник, а
основание высоты совпадает с центром основания.
Осью правильной пирамиды называется прямая, содержащая её
высоту.
Правильная треугольная пирамида называется тетраэдром.
Если пирамиду пересечь плоскостью,
параллельной плоскости основания, то она
отсечет пирамиду, подобную данной.
Оставшаяся часть называется усеченной
пирамидой.

4.

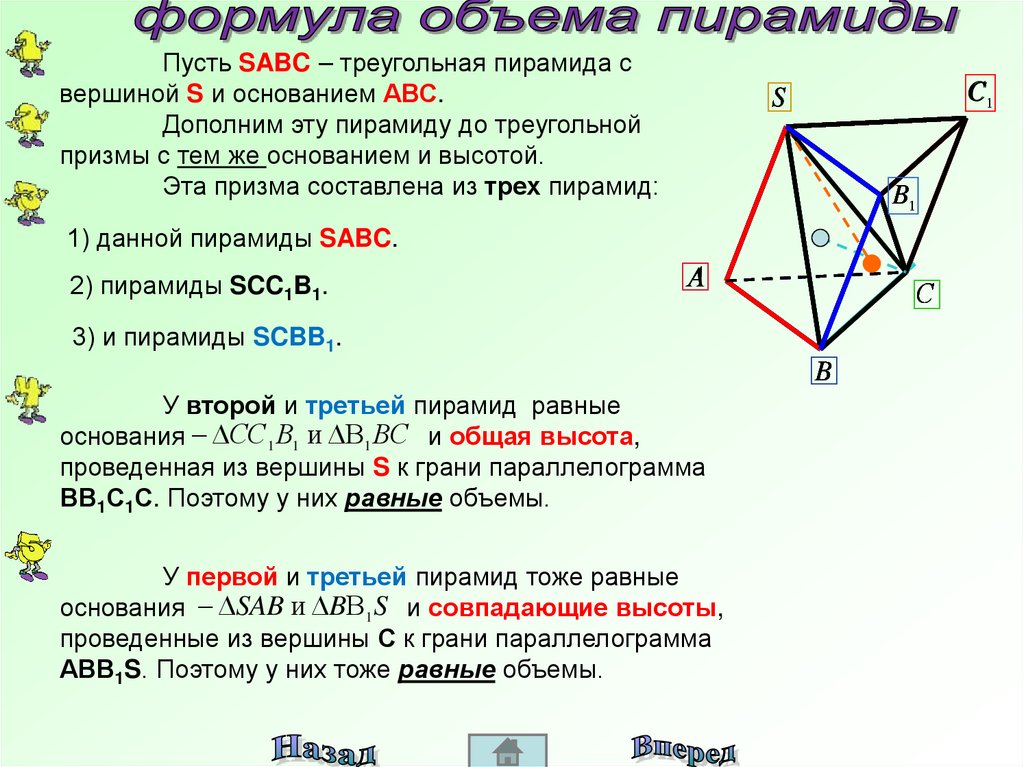
Пусть SABC – треугольная пирамида с
вершиной S и основанием АВС.
Дополним эту пирамиду до треугольной
призмы с тем же основанием и высотой.
Эта призма составлена из трех пирамид:
C1
С
S
B1
1) данной пирамиды SABC.
2) пирамиды SCC1B1.
A
А
С
3) и пирамиды SCBB1.
B
У второй и третьей пирамид равные
основания СС1 В1 и В1 ВС и общая высота,
проведенная из вершины S к грани параллелограмма
ВВ1С1С. Поэтому у них равные объемы.
У первой и третьей пирамид тоже равные
основания SAB и BВ1 S и совпадающие высоты,
проведенные из вершины С к грани параллелограмма
АВВ1S. Поэтому у них тоже равные объемы.

5.

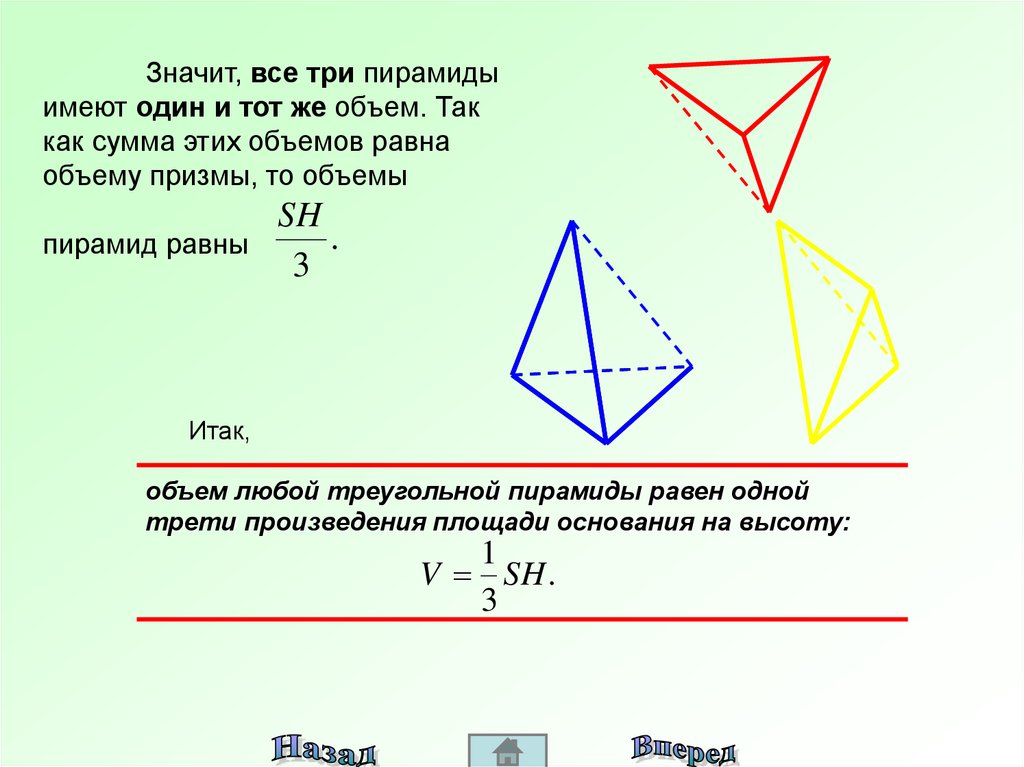
Значит, все три пирамиды
имеют один и тот же объем. Так
как сумма этих объемов равна
объему призмы, то объемы
SH
.
пирамид равны
3
Итак,
объем любой треугольной пирамиды равен одной
трети произведения площади основания на высоту:
1
V SH .
3

6.

1) Пусть теперь имеем любую, не обязательно треугольную
пирамиду.
2) Разобьем ее основание на треугольники
1 , 2 ,..., n .
3) Пирамиды, у которых основаниями являются эти треугольники, а
вершинами – вершина данной пирамиды, составляют данную
пирамиду.
4) Объем данной пирамиды равен сумме объемов
составляющих ее пирамид. Так как все они имеют ту же высоту
H, что и данная пирамида, то объем ее равен:
V V1 V2 ... Vn
1
1
1
V S1 H S 2 H ... S n H
3
3
3
1
1
V H S1 S 2 ... S n S H .
3
3
6
5
n
1
1
22
4 4
объем любой пирамиды равен одной трети
произведения площади основания на высоту.
33

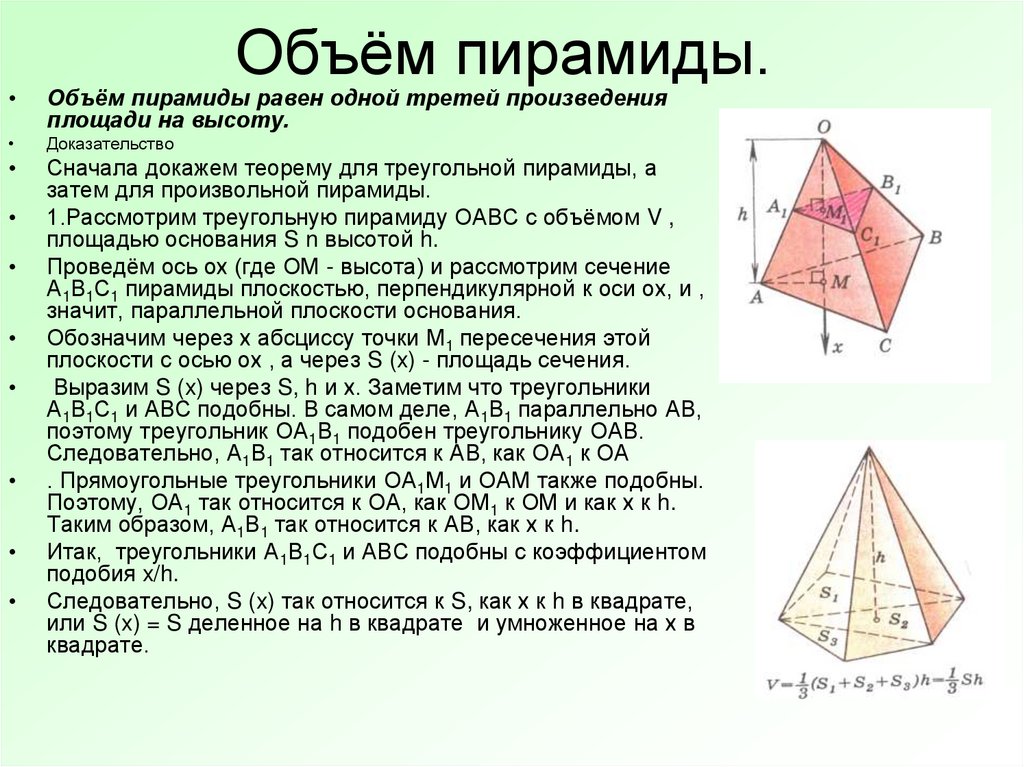
7. Объём пирамиды.

Объём пирамиды равен одной третей произведения
площади на высоту.
Доказательство
Сначала докажем теорему для треугольной пирамиды, а
затем для произвольной пирамиды.
1.Рассмотрим треугольную пирамиду ОАВС с объёмом V ,
площадью основания S n высотой h.
Проведём ось ох (где ОМ - высота) и рассмотрим сечение
А1В1С1 пирамиды плоскостью, перпендикулярной к оси ох, и ,
значит, параллельной плоскости основания.
Обозначим через х абсциссу точки М1 пересечения этой
плоскости с осью ох , а через S (x) - площадь сечения.
Выразим S (x) через S, h и х. Заметим что треугольники
А1В1С1 и АВС подобны. В самом деле, А1В1 параллельно АВ,
поэтому треугольник ОА1В1 подобен треугольнику ОАВ.
Следовательно, А1В1 так относится к АВ, как ОА1 к ОА
. Прямоугольные треугольники ОА1М1 и ОАМ также подобны.
Поэтому, ОА1 так относится к ОА, как ОМ1 к ОМ и как х к h.
Таким образом, А1В1 так относится к АВ, как х к h.
Итак, треугольники А1В1С1 и АВС подобны с коэффициентом
подобия x/h.
Следовательно, S (x) так относится к S, как х к h в квадрате,
или S (x) = S деленное на h в квадрате и умноженное на х в
квадрате.

8. Докажем теперь теорему для произвольной пирамиды с высотой h и площадью основания S. Пирамиду можно разбить на треугольные

Применяя теперь основную формулу для вычисления объёмов тел при а=0, в
=h, получаем
Докажем теперь теорему для произвольной пирамиды с высотой h и
площадью основания S. Пирамиду можно разбить на треугольные
пирамиды с высотой h. Выразим объём каждой треугольной пирамиды по
доказанной нами формуле и сложим эти объёмы. Вынося за скобки общий
множитель 1/3 h, получим в скобках сумму площадей оснований
треугольных пирамид, т.е. площадь S основание исходной пирамиды.
Таким образом объём исходной пирамиды равен 1\3 Sh. Теорема
доказана.

9.

10.

11.

R
А
О
а АО а 3
3
а2 3
S
4
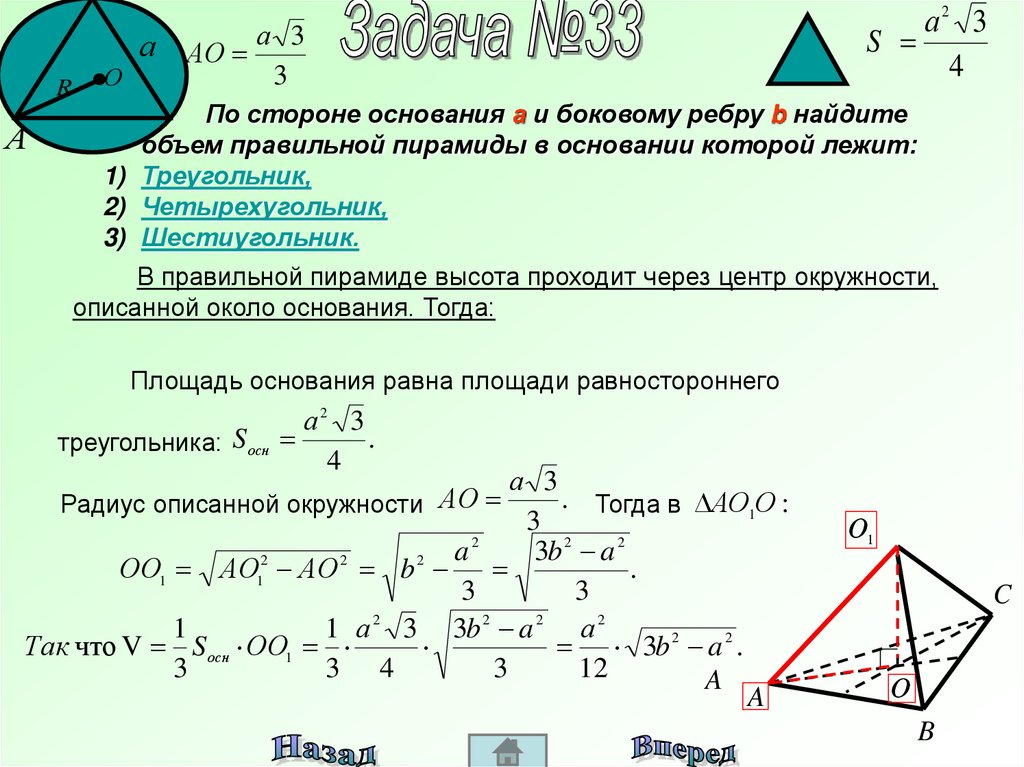
По стороне основания а и боковому ребру b найдите
объем правильной пирамиды в основании которой лежит:
1) Треугольник,
2) Четырехугольник,
3) Шестиугольник.
В правильной пирамиде высота проходит через центр окружности,
описанной около основания. Тогда:
Площадь основания равна площади равностороннего
а2 3
.
треугольника: S осн
4
а 3
. Тогда в АО1О :
3
2
a
3b 2 a 2
2
2
2
ОО1 АО1 АО b
.
3
3
1
1 а 2 3 3b 2 a 2 а 2
Так что V S осн ОО1
3b 2 a 2 .
3
3 4
3
12
A
A
Радиус описанной окружности АО
O1
C
O
B

12.

В правильной пирамиде высота проходит через центр окружности,
описанной около основания. Тогда:
Основание – квадрат с площадью Sосн=а2. Радиус описанной
окружности АО равен половине диагонали квадрата:
АО
АС а 2
. Далее, в АОО1 :
2
2
a2
2b 2 a 2
ОО1 АО АО b
. Так что
2
2
1
1
2b 2 a 2
a2
2
V S осн ОО1 а
4b 2 2a 2 .
3
3
2
6
2
1
2
2
O1
а
а
S осн а 2
О
D
A
А
C
O
B
АО
а 2
2

13.

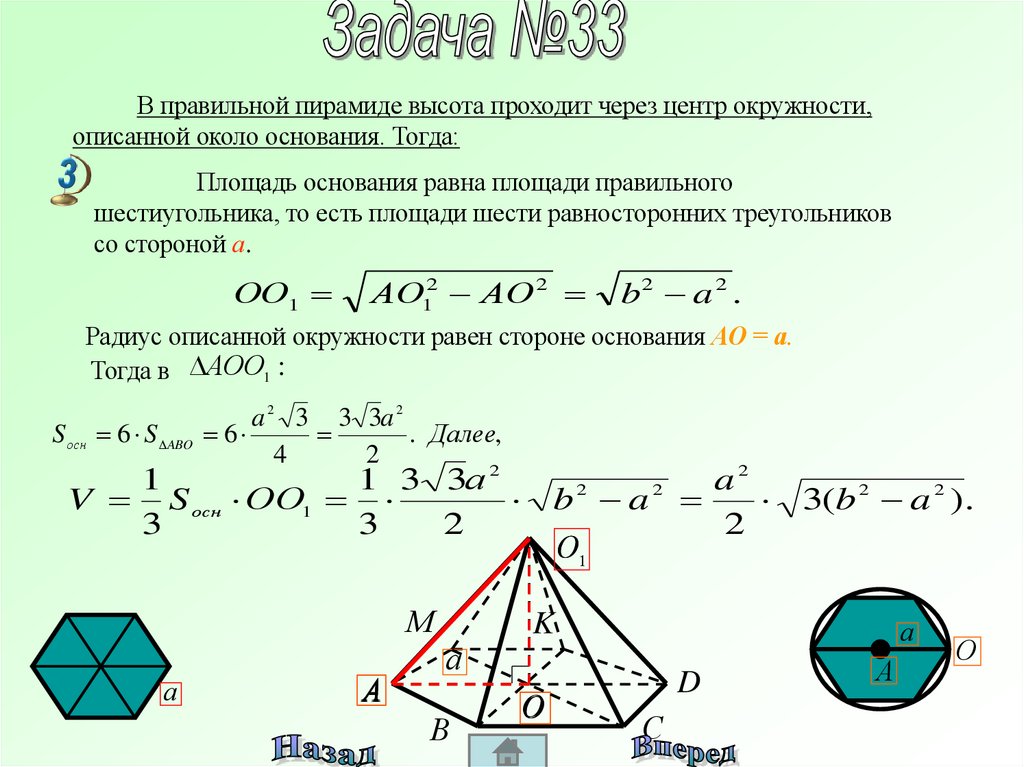
В правильной пирамиде высота проходит через центр окружности,
описанной около основания. Тогда:
Площадь основания равна площади правильного
шестиугольника, то есть площади шести равносторонних треугольников
со стороной а.
ОО1
АО12 АО 2
b2 a 2 .
Радиус описанной окружности равен стороне основания АО = а.
Тогда в АОО1 :
a 2 3 3 3a 2
S осн 6 S ABO 6
. Далее,
4
2
2
2
1
1 3 3а
a
V S осн ОО1
b2 a2
3(b 2 a 2 ).
3
3
2
2
О1
М
а
А
K
а
а
В
О
D
С
А
О

14.

Проведем высоту пирамиды О1О. В правильной пирамиде высота проходит
через центр окружности, вписанной в основание.
Тогда проведем ОЕ .АВ
По теореме о трех перпендикулярах О1 Е АВ.Так что ОЕ – радиус
вписанной окружности, а О1 ЕО 45 как линейный угол данного двугранного угла.
a
a
a 3
a
.
r
2tg 30 2 1
2
О
Е
Далее в О1ОЕ :
3
a 3
ОО1 ОЕ
(так как О1ОЕ равнобедренный ).
2
Тогда ОЕ r
Далее площадь основания равна площади 6
равносторонних треугольников со стороной а:
3 3a 2
S осн 6 S ABO
. Так что
2 2
1
1 3 3a а 3 3 3
V S осн ОО1
а.
3
3
2
2
4
М
А
45
Е
В
О1
K
D
О
С

15.

R
b
180
r О
2 sin
n
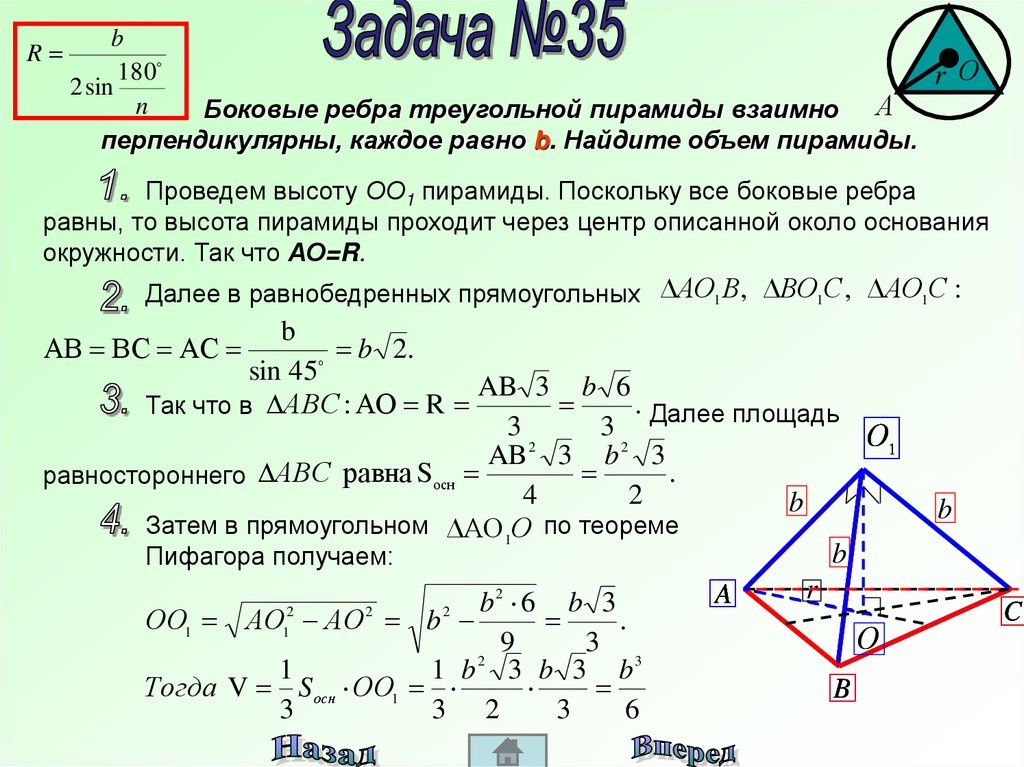
Боковые ребра треугольной пирамиды взаимно А
перпендикулярны, каждое равно b. Найдите объем пирамиды.
Проведем высоту ОО1 пирамиды. Поскольку все боковые ребра
равны, то высота пирамиды проходит через центр описанной около основания
окружности. Так что АО=R.
Далее в равнобедренных прямоугольных АО1 В, ВО1С , АО1С :
b
АВ ВС АС
b 2.
sin 45
AB 3 b 6
. Далее площадь
Так что в АВС : АО R
3
3
О1
2
AB 3 b 2 3
.
равностороннего АВС равна Sосн
4
2
b
Затем в прямоугольном АО 1О по теореме
b
Пифагора получаем:
r
A
b2 6 b 3
2
2
2
ОО1 АО1 АО b
.
О
9
3 3
2
1
1 b 3 b 3 b
Тогда V S осн ОО1
B
3
3 2
3
6
b
C

16.

О2
О2
h
А
D
О1
В
С

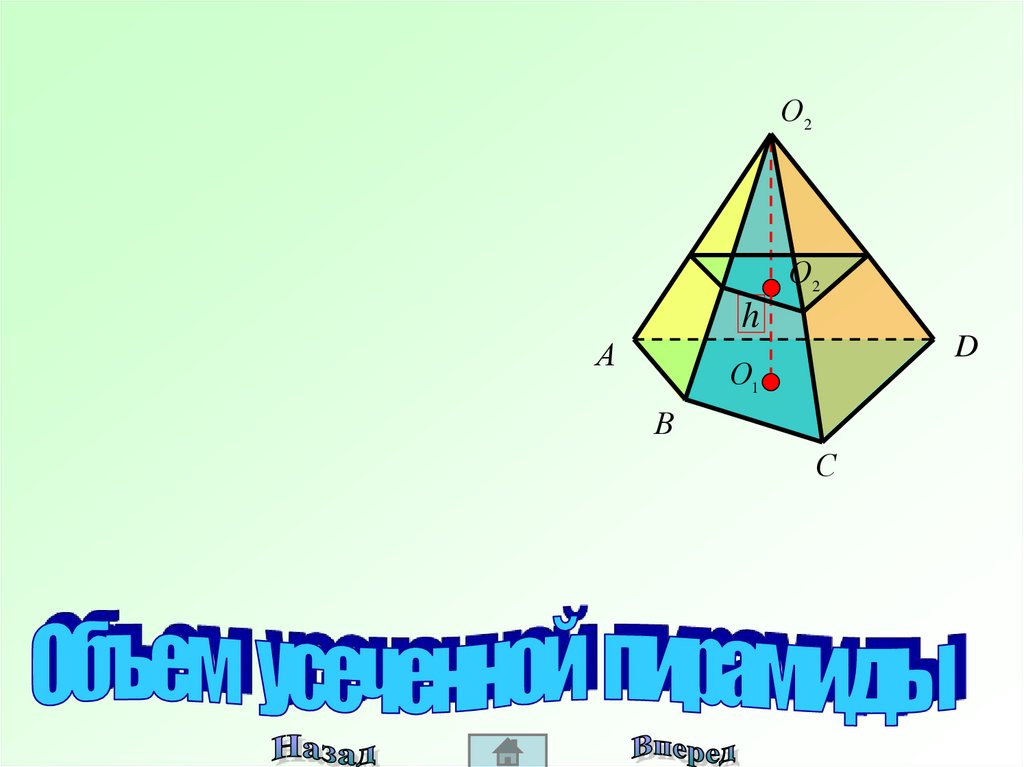
17.

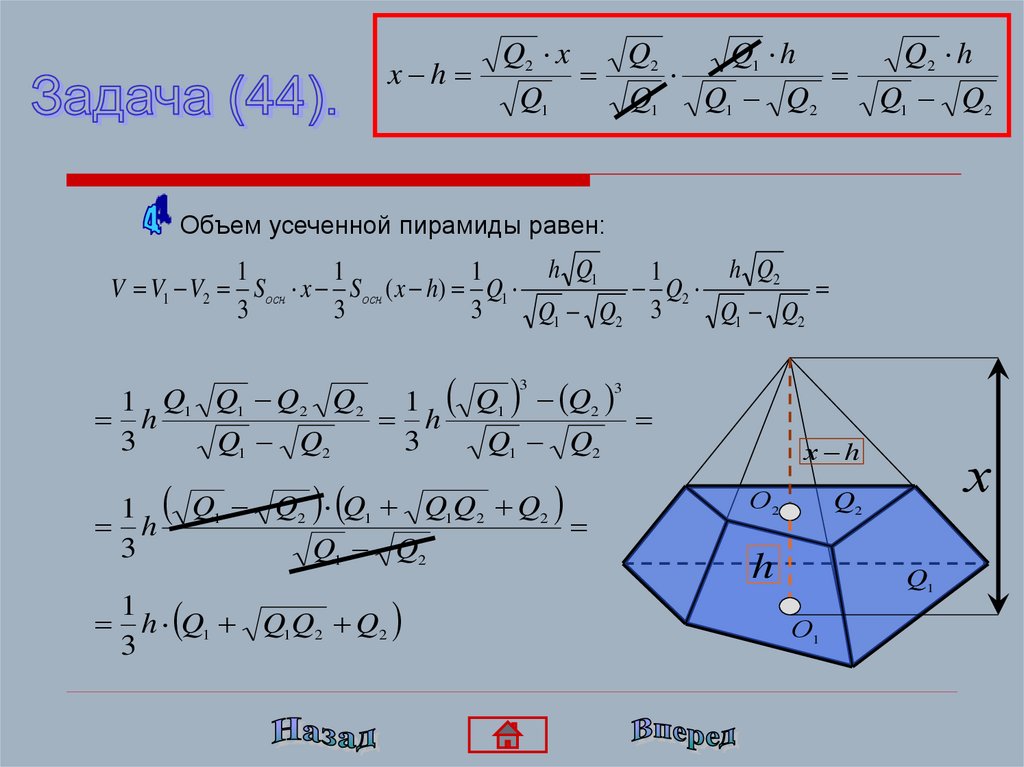
Найдите объем усеченной пирамиды с площадями оснований
Q1 и Q2 (Q1>Q2) и высотой h.
Решение:
Дополним данную усеченную пирамиду до полной.
Пусть х – ее высота. Объем усеченной пирамиды равен разности
объемов двух полных пирамид: одной с площадью основания Q1 и
высотой х, другой с площадью основания Q2 и высотой х – h.
Из подобия этих пирамид находим х:
Q1 x
Q2 x h
2
Q `1 x Q1 h Q2 x
Q `1 x Q2 х Q1 h
Q`1 ( x h) 2 Q2 x 2 х Q Q Q h
1
2
1
Q `1 ( x h) Q2 x
Q1 h
х
Q1 Q2
х h
О2
х
Q2
h
Q1
О1

18.

Q2 x
Q2
Q1 h
Q2 h
x h
Q1
Q1
Q1 Q2
Q1 Q2
Объем усеченной пирамиды равен:
h Q1
h Q2
1
1
1
1
V V1 V2 S осн x S осн ( x h) Q1
Q2
3
3
3
Q1 Q2 3
Q1 Q2
1 Q1 Q1 Q2 Q2 1 Q1 Q2
h
h
3
3
Q1 Q2
Q1 Q2
3
1 Q1 Q2 Q1 Q1Q2 Q2
h
3
Q1 Q2
1
h Q1 Q1Q2 Q2
3
3
х h
О2
х
Q2
h
Q1
О1

19.

Первым из наших современников, кто
установил ряд необычных явлений,
связанных с пирамидой, был
французский ученый Антуан Бови.
Исследуя пирамиду Хеопса в 30-х
годах двадцатого столетия, он
обнаружил, что тела мелких
животных, случайно попавших в
царскую комнату,
мумифицировались. Причину этого
Бови объяснил для себя формой
пирамиды и, как оказалось не
ошибся. Его труды легли в основу
современных исследований, в
результате которых за последние 20
лет появилось множество книг и
публикаций, подтверждающих, что
энергия пирамид может иметь
прикладное значение.

20.

21.

По утверждению большинства исследователей, все это
является доказательством существования энергии
пирамид.
За 5000 лет своего существования, пирамиды
превратились в некий символ, олицетворяющий
стремление человека достичь вершины знаний. Надеюсь,
что пирамида будет напоминать вам об этом, и поможет
покорить свои вершины, только проявите настойчивость,
благодаря
которой,
содержимое
каменоломен
превратилось в пирамиду Хеопса.