ЛЕКЦИЯ 5 магнитостатика

1.

1

2.

2

3. МАГНИТНОЕ ПОЛЕ

• 1. Магнитостатика
• 2. Электромагнетизм
Магнитное поле, в отличие от
электрического поля, оказывает силовое
действие только на движущиеся заряды
(токи).
3

4. Магнитостатика

4

5. 1. Магнитное поле и его характеристики

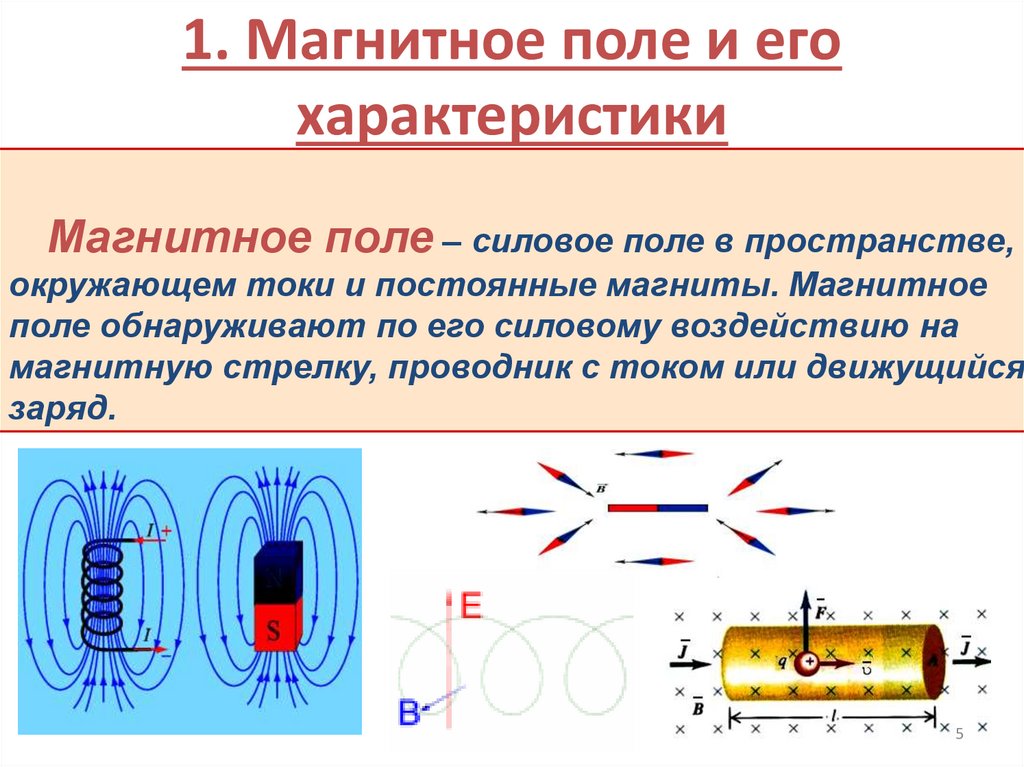
Магнитное поле – силовое поле в пространстве,
окружающем токи и постоянные магниты. Магнитное
поле обнаруживают по его силовому воздействию на
магнитную стрелку, проводник с током или движущийся
заряд.
5

6. ХАРАКТЕРИСТИКИ МАГНИТНОГО ПОЛЯ

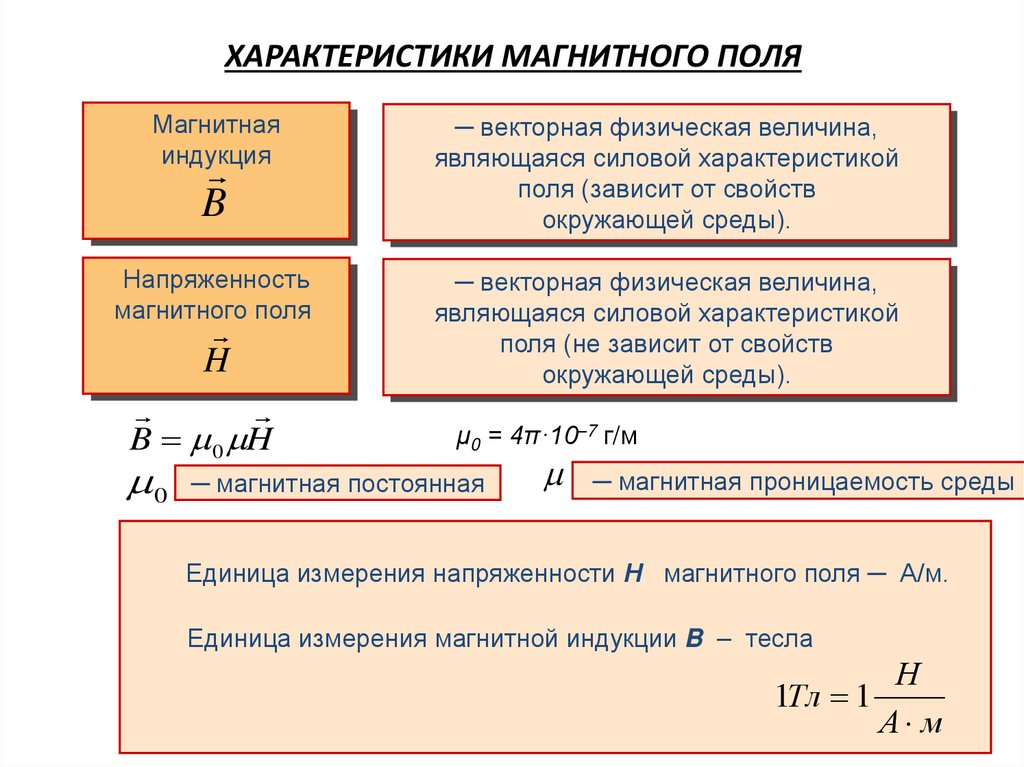
Магнитная
индукция
─ векторная физическая величина,
являющаяся силовой характеристикой
поля (зависит от свойств
окружающей среды).
Напряженность
магнитного поля
─ векторная физическая величина,
являющаяся силовой характеристикой
поля (не зависит от свойств
окружающей среды).
B
H
B 0 H
μ0 = 4π·10–7 г/м
0 ─ магнитная постоянная
─ магнитная проницаемость среды
Единица измерения напряженности Н магнитного поля ─ А/м.
Единица измерения магнитной индукции B – тесла
Н
1Тл 1
А м

7. Магнитная индукция

Силовой характеристикой магнитного поля
является вектор магнитной индукции
Вектор магнитной индукции
определяет силы,
действующие на токи или движущиеся заряды в
магнитном поле.
За
положительное
направление
вектора
магнитной индукции принимается направление от
южного полюса S к северному полюсу N магнитной
стрелки,
свободно
устанавливающейся
в
магнитном поле.

8. Кроме вектора магнитной индукции, магнитное поле характеризуется вектором напряженности

где μ0 – магнитная постоянная.
в СИ μ0 = 4π·10–7 г/м ≈ 1,26·10–6 H/A2 B μμ0 H
Аналогично силовым линиями в электростатике, можно
построить силовые линии - линии магнитной индукции.
Магнитное поле изображается линиями магнитной
индукции, т.е. линиями, касательная в каждой точке
к которым совпадает с направлением вектора
магнитной индукции.
Линии магнитной индукции всегда замкнуты, они
нигде не обрываются. Это означает, что магнитное поле не имеет источников (магнитных зарядов) . Такие силовые поля- вихревые.
8

9.

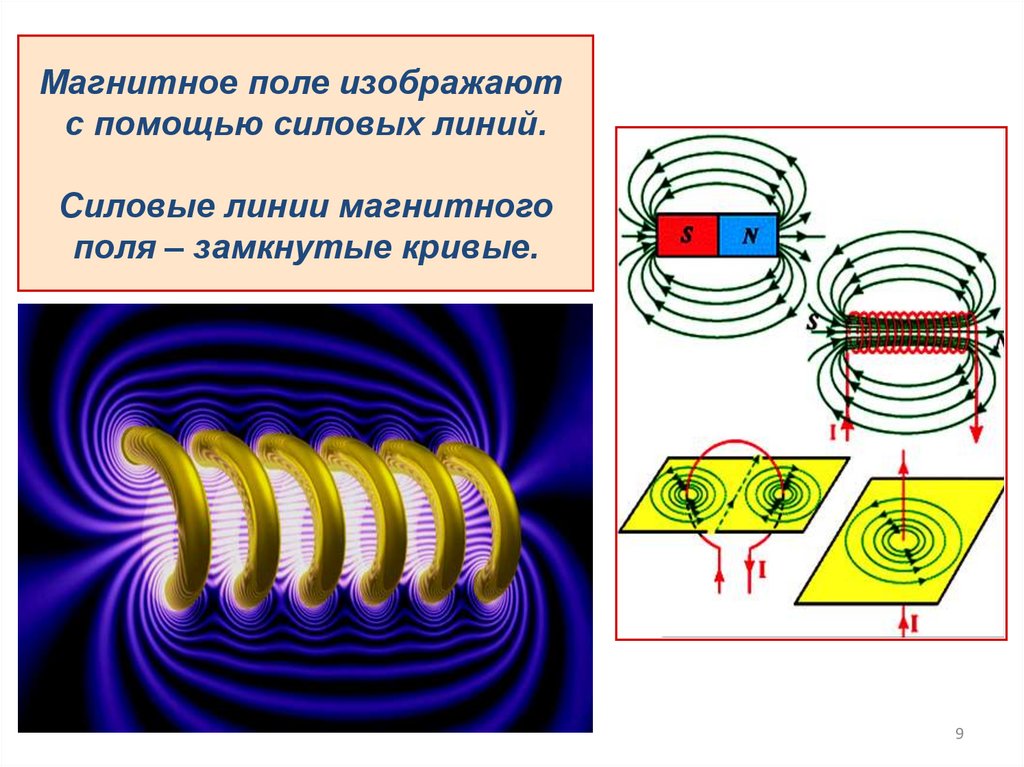
Магнитное поле изображают
с помощью силовых линий.
Силовые линии магнитного
поля – замкнутые кривые.
9

10.

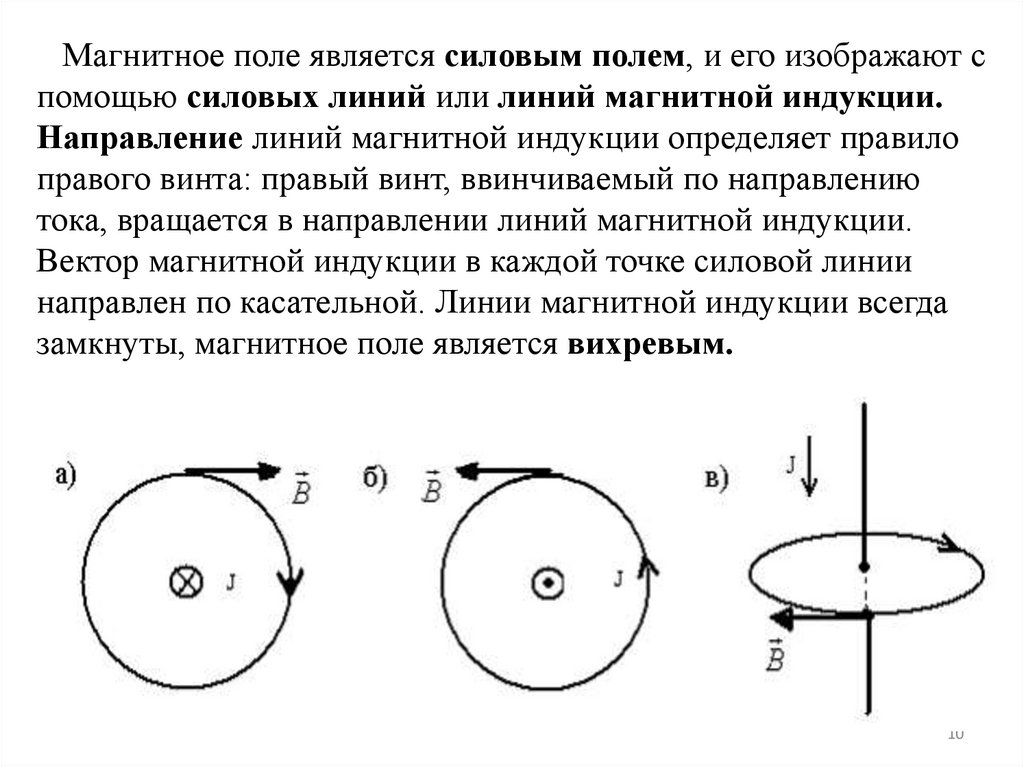
Магнитное поле является силовым полем, и его изображают с
помощью силовых линий или линий магнитной индукции.
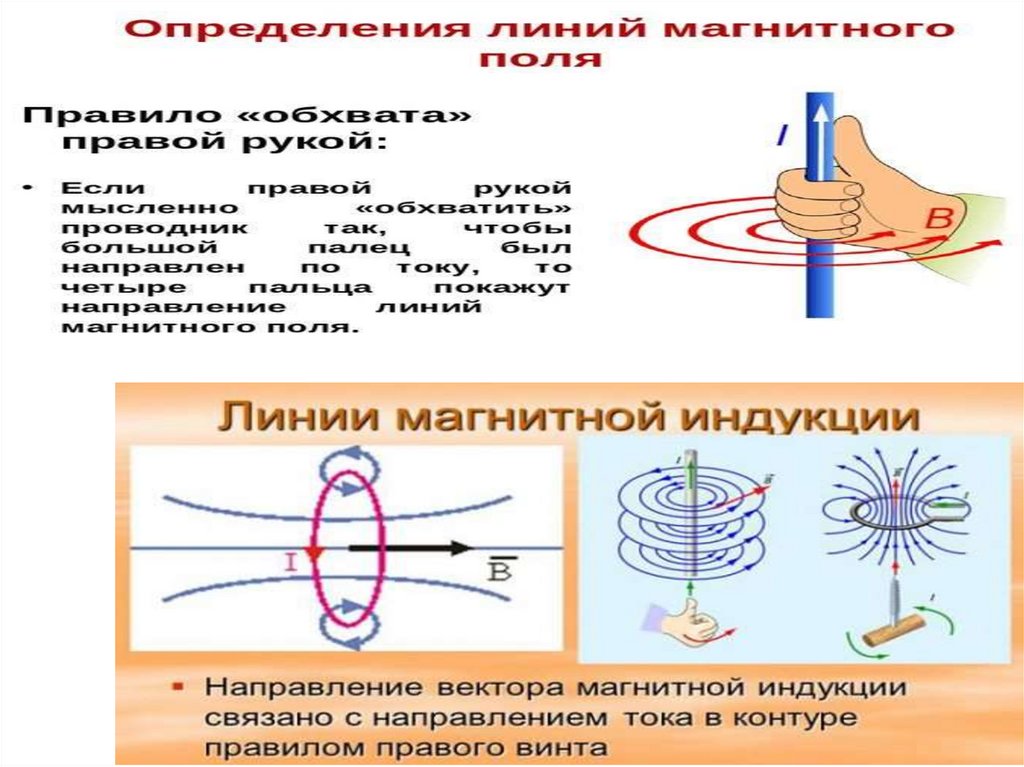
Направление линий магнитной индукции определяет правило
правого винта: правый винт, ввинчиваемый по направлению
тока, вращается в направлении линий магнитной индукции.
Вектор магнитной индукции в каждой точке силовой линии
направлен по касательной. Линии магнитной индукции всегда
замкнуты, магнитное поле является вихревым.
10

11.

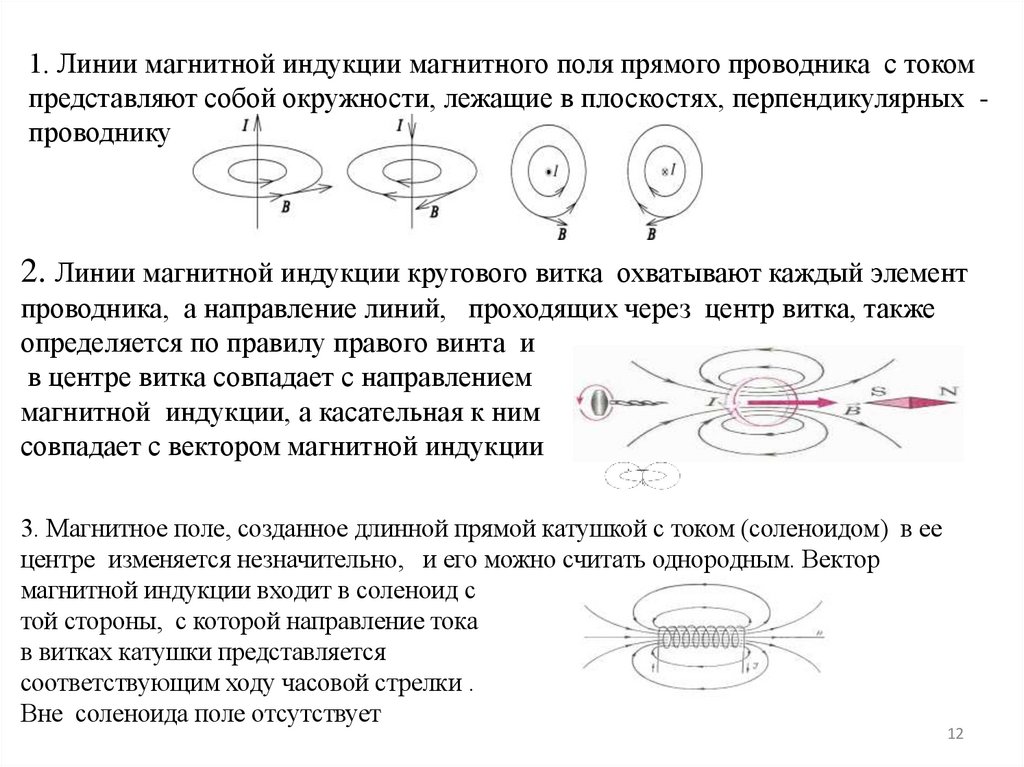
11

12. 1. Линии магнитной индукции магнитного поля прямого проводника с током представляют собой окружности, лежащие в плоскостях,

перпендикулярных проводнику
2. Линии магнитной индукции кругового витка охватывают каждый элемент
проводника, а направление линий, проходящих через центр витка, также
определяется по правилу правого винта и
в центре витка совпадает с направлением
магнитной индукции, а касательная к ним
совпадает с вектором магнитной индукции
3. Магнитное поле, созданное длинной прямой катушкой с током (соленоидом) в ее
центре изменяется незначительно, и его можно считать однородным. Вектор
магнитной индукции входит в соленоид с
той стороны, с которой направление тока
в витках катушки представляется
соответствующим ходу часовой стрелки .
Вне соленоида поле отсутствует
12

13.

13

14. 2. Действие магнитного поля на проводники с током. Сила Ампера

Модуль вектора магнитной индукции равен отношению
максимального значения силы Ампера, действующей на
прямой проводник с током, к силе тока I в проводнике и его
длине Δl:
В системе единиц СИ за единицу магнитной индукции
принята индукция такого магнитного поля, в котором на
каждый метр длины проводника при силе тока 1 А
действует максимальная сила Ампера 1 Н. Эта единица
Н
называется тесла (Тл).
1Тл 1
А м
14

15.

Основное проявление магнитного поля состоит в его
силовом действии на электрические токи и движущиеся
заряды. Ампер в результате обобщения экспериментальных данных установил, от чего зависит величина этого
действия. По закону Ампера на элемент проводника dl с
током I, помещенный в магнитное поле В, действует сила
Ампера:
Сила, действующая на прямолинейный проводник
длины l, находится интегрированием соотношения,
записаного выше :
15

16.

16

17.

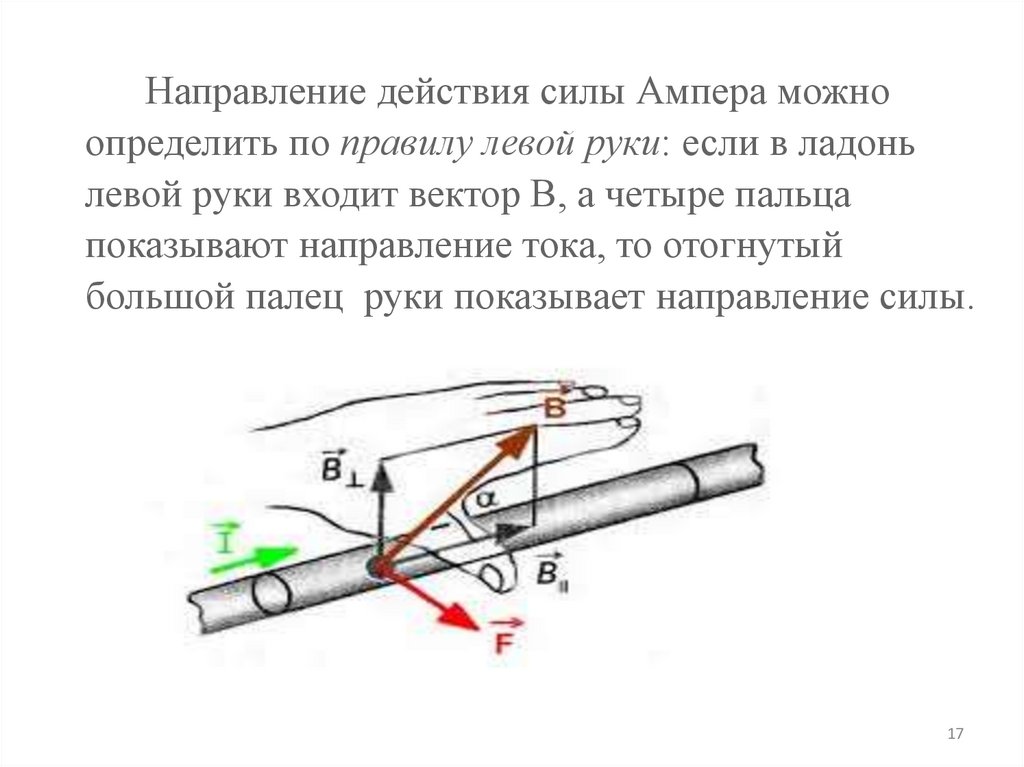
Направление действия силы Ампера можно
определить по правилу левой руки: если в ладонь
левой руки входит вектор В, а четыре пальца
показывают направление тока, то отогнутый
большой палец руки показывает направление силы.
17

18. 3. Действие магнитного поля на движущиеся заряды. Сила Лоренца.

Bажнейшая особенность магнитного поля
состоит в том, что оно действует только на
движущиеся электрические заряды. В результате опытов было установлено, что любая
заряженная частица, движущаяся в магнитном
поле, испытывает действие силы F, которая
пропорциональна величине магнитного поля в
этой точке. Направление этой силы всегда
перпендикулярно скорости движения частицы и
зависит от угла между направлениями
18

19.

Эта сила называется силой Лоренца
модуль силы Лоренца
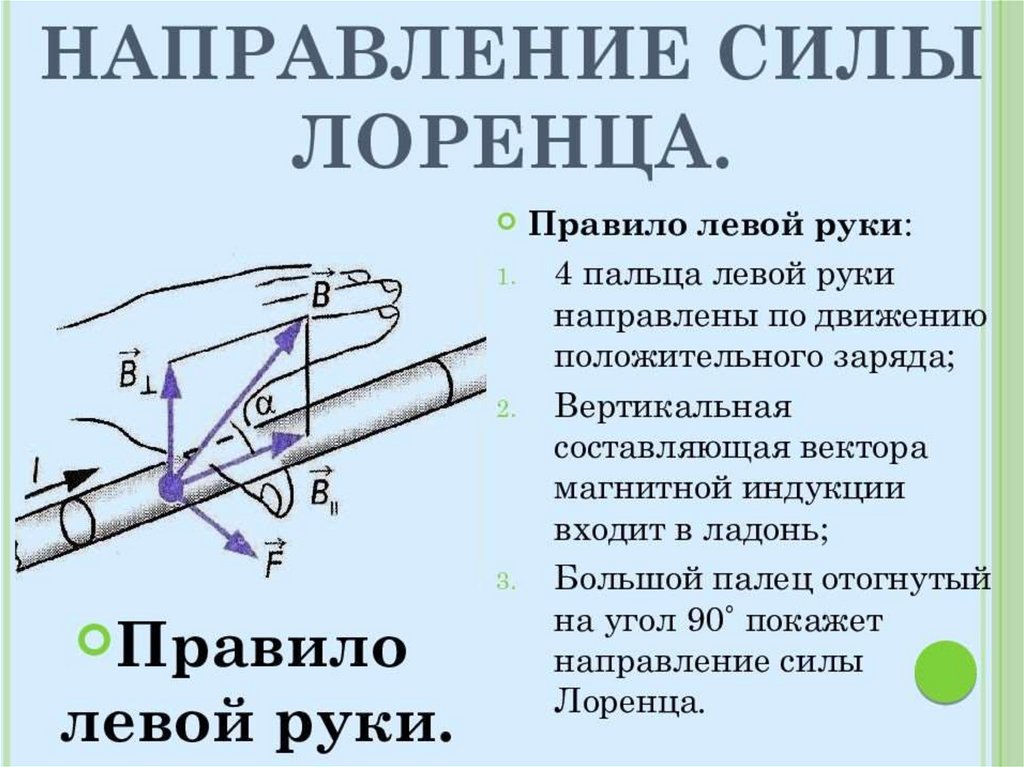
Направление силы Лоренца определяется по правилу
левой руки: четыре пальца левой руки – по скорости,
вектор
входит в ладонь, отогнутый под прямым
углом большой палец покажет направление силы
Лоренца для положительного заряда. Для отрицательного заряда – четыре пальца против скорости, дальше
то же, что и для
положительного заряда.
19

20.

На заряд q, движущийся со скоростью V в магнитном
поле с индукцией B, действует сила Лоренца.
20

21.

21

22.

Сила Лоренца
В соответствии с законом Ампера сила, действующая на
элемент тока
определяется по формуле
Учтём, что элементарный ток есть не что иное, как направленное
движение электрических зарядов
где V – объём, n – концентрация
носителей, j – плотность тока, S –
площадь поперечного сечения
проводника, e – заряд электрона (e =
1,6·10-19 Кл), dl - длина элемента
проводника,
- скорость
направленного движения электронов.
22

23.

Cила Лоренца
действует на отдельно взятый
электрический заряд со стороны магнитного поля.
Fл = FA /N , где N- число зарядов
FA =IBlsinɑ I =Nq/Δt, тогда FA = Nq/Δt Blsin ɑ
Fл = FA /N = (N q/Δt Blsinɑ)/N = q(l/Δt )Blsin ɑ =
qVB sinɑ , или в векторном виде Fл =q [ V x B] .
Так как сила Лоренца перпендикулярна скорости
частицы, то она не совершает работы. Согласно
теореме о кинетической энергии это означает, что
сила Лоренца не меняет кинетическую энергию
частицы и, следовательно, модуль ее скорости. Под
действием силы Лоренца меняется лишь направление
скорости частицы.
23

24.

24

25.

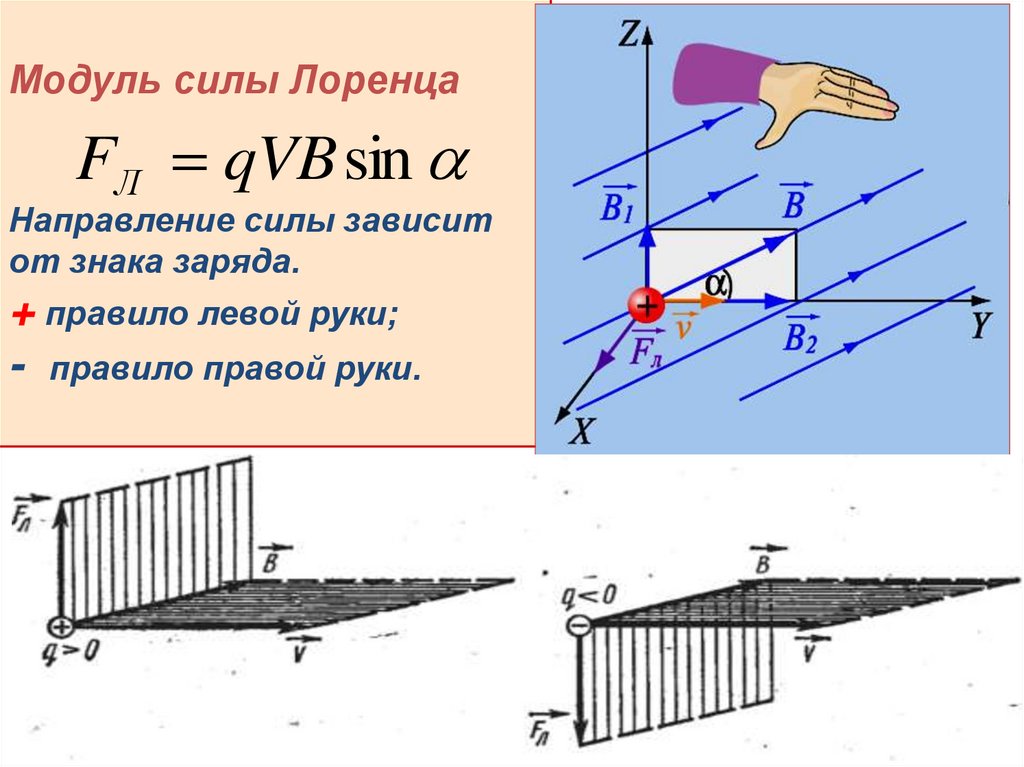
Модуль силы Лоренца
FЛ qVB sin
Направление силы зависит
от знака заряда.
+ правило левой руки;
- правило правой руки.
25

26.

26

27.

Считаем, что магнитное поле однородно и
на частицу не действуют электрические
поля. Рассмотрим три возможных случая:
1) Заряженная частица движется в магнитном
поле вдоль линий магнитной индукции
2) Заряженная частица движется в
магнитном поле со
скоростью
3) Заряженная частица движется под углом к
линиям магнитной индукции .
27

28. Рассмотрим эти случаи: 1. Магнитное поле не действует на заряженную частицу в двух случаях : если частица неподвиж-на (V=0) или

Рассмотрим эти случаи:
1. Магнитное поле не действует на заряженную
частицу в двух случаях : если частица неподвижна (V=0) или если частица движется вдоль силовой линии магнитного поля. (V и B параллельны).
При таком движении частицы угол а между векторами её скоростиV и индукции В равен 0 град.
0 sin 0 FЛ 0
Поэтому сила Лоренца равна нулю, т.е. магнитное
поле не действует на частицу. Она будет двигаться по инерции – равномерно и прямолинейно.
2. Частица, имеющая заряд q, движется перпендикулярно к линиям магнитной индукции .
28е

29.

Поскольку в однородном поле В = const, а численное значение скорости заряда в магнитном поле не
изменяется (V=const), то радиус кривизны траектории этого заряда постоянный. Поэтому заряженная частица будет двигаться по окружности,
плоскость которой перпендикулярна к магнитному
полю, а радиус прямо пропорционален скорости
частицы и обратно пропорционален произведению
ее её удельного заряда на индукцию В поля.
R=mv/qB
.
29

30.

Направление магнитной силы и направление
вызываемого ею отклонения заряженной
частицы в магнитном поле зависит от знака
заряда q частицы.
Если частица движется в
плоскости чертежа слева
направо, а магнитное поле
направлено из-за чертежа
перпендикулярно к его
плоскости, то при q > 0
частица отклоняется вниз, а
при q < 0 - вверх.
30

31.

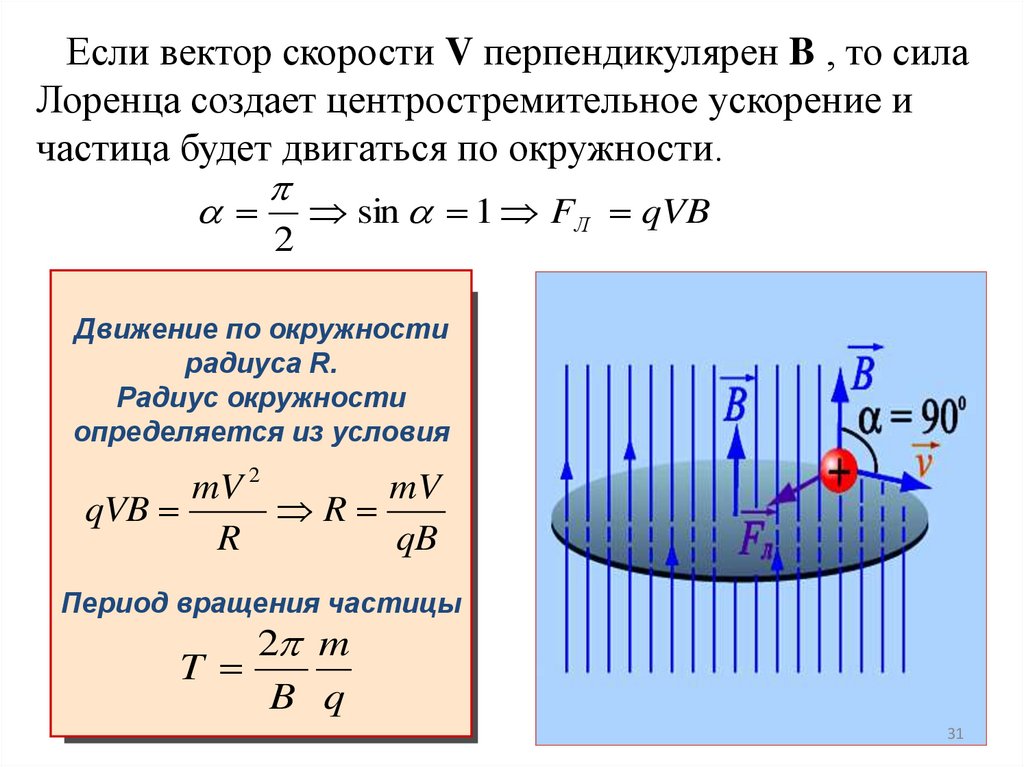
Если вектор скорости V перпендикулярен B , то сила
Лоренца создает центростремительное ускорение и
частица будет двигаться по окружности.
sin 1 FЛ qVB
2
Движение по окружности
радиуса R.
Радиус окружности
определяется из условия
mV 2
mV
qVB
R
R
qB
Период вращения частицы
2 m
T
B q
31

32.

3. Если скорость частицы направлена под углом к B ,
то заряженная частица движется по спирали, ось которой параллельна магнитному полю.
Движение частицы под углом к направлению вектора
магнитной индукции состоит из двух движений:
1) равномерного движения по окружности;
2) равномерного прямолинейного движения вдоль поля
В результате сложения этих двух движений
возникает движение по винтовой линии.
32

33.

Магнитное поле Земли
33

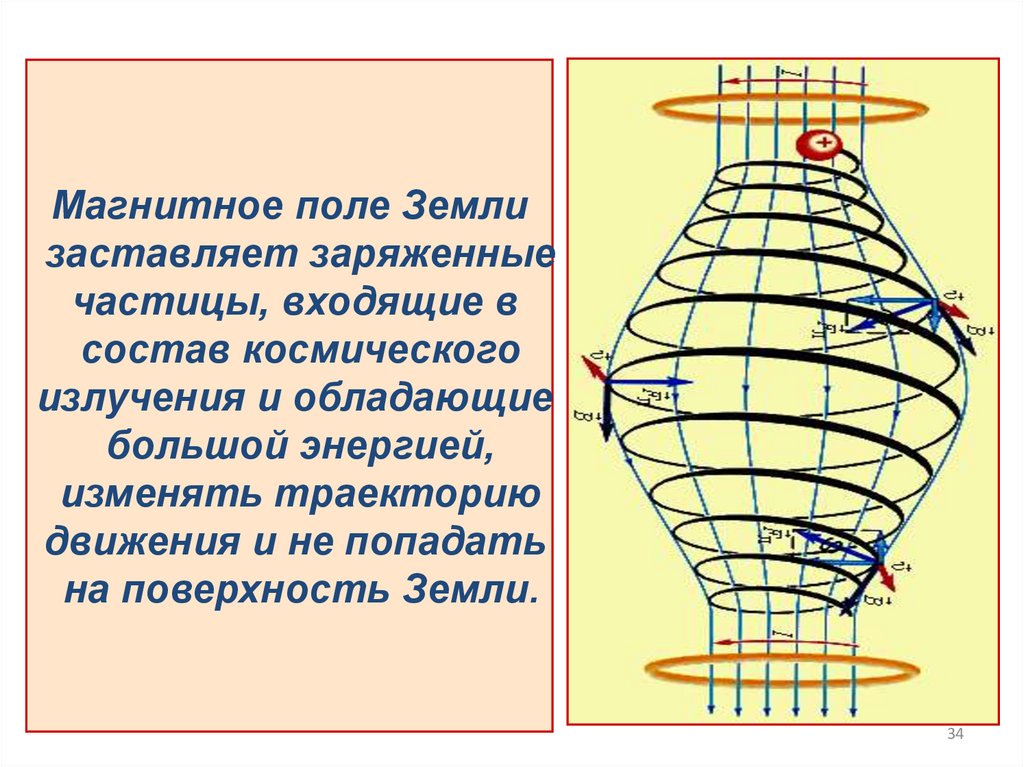
34.

Магнитное поле Земли
заставляет заряженные
частицы, входящие в
состав космического
излучения и обладающие
большой энергией,
изменять траекторию
движения и не попадать
на поверхность Земли.
34

35.

Магнитное поле Земли, образующее земную
магнитосферу, простирается на расстоянии 70
– 80 тысяч км в направлении к Солнцу и на
многие миллионы километров в обратном
направлении. В околоземном пространстве
магнитное поле образует магнитную ловушку
для заряженных частиц высоких энергий.
Происхождение магнитного поля Земли
связывают с движениями проводящего жидкого
вещества в земном ядре.
Из других планет Солнечной системы лишь
Юпитер и Сатурн обладают заметными магнитными полями.
35

36.

Действие магнитного поля Земли вблизи земной
поверхности изменяет траекторию движения частиц,
испускаемых Солнцем и звездами. Этим объясняется
так называемый широтный эффект, заключающийся в
том, что интенсивность космических лучей, доходящих до Земли, вблизи экватора меньше, чем в более
высоких широтах.
Действием магнитного поля Земли объясняется тот
факт, что полярное сияние наблюдается только в
самых высоких широтах, на Крайнем Севере. Именно
в том направлении магнитное поле Земли отклоняет
заряженные космические частицы, которые вызывают
свечение атмосферы, называемое полярным сиянием.
36

37.

37

38.

38

39.

39

40.

40

41.

41

42.

42

43.

43

44. 4. Закон Био–Савара-Лапласа

Французские физики Ф. Савар и Ж.Б. Био
изучали
магнитное
поле,
создаваемое
проводниками с постоянным током различной
формы. На основании многочисленных опытов
они пришли к выводу, что магнитная индукция
поля проводника с током
• пропорциональна силе тока I,
• зависит от формы и размеров проводника,
• также от расположения рассматриваемой
точки по отношению к проводнику.
44

45.

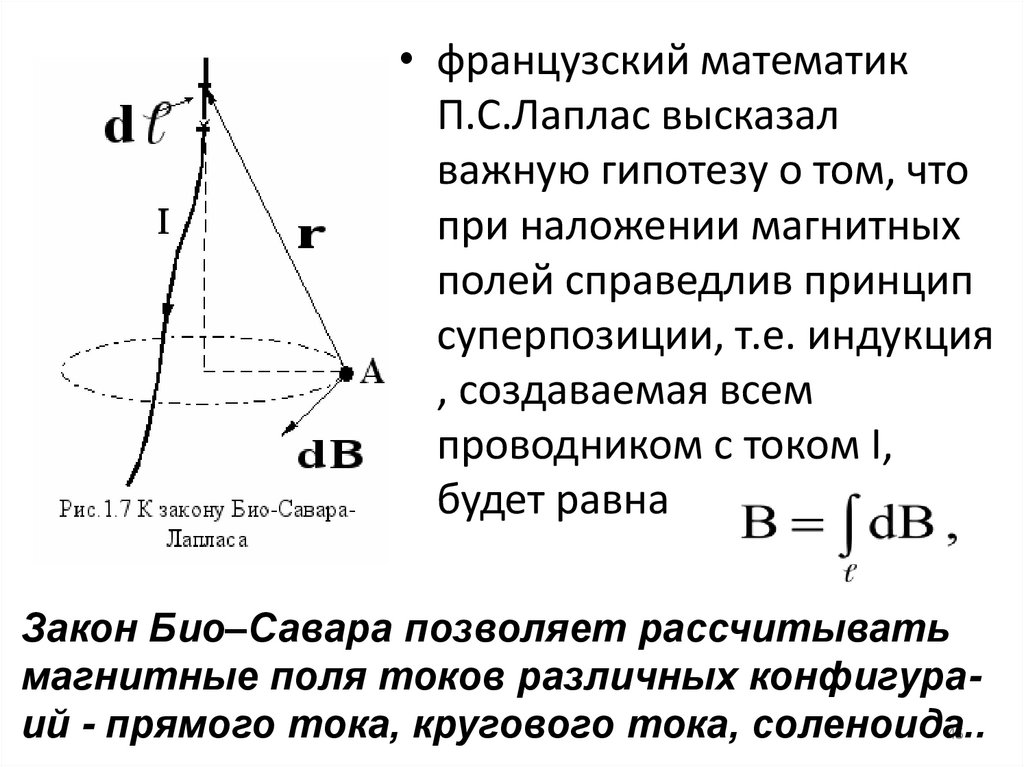
• французский математик
П.С.Лаплас высказал
важную гипотезу о том, что
при наложении магнитных
полей справедлив принцип
суперпозиции, т.е. индукция
, создаваемая всем
проводником с током I,
будет равна
Закон Био–Савара позволяет рассчитывать
магнитные поля токов различных конфигураий - прямого тока, кругового тока, соленоида..
45

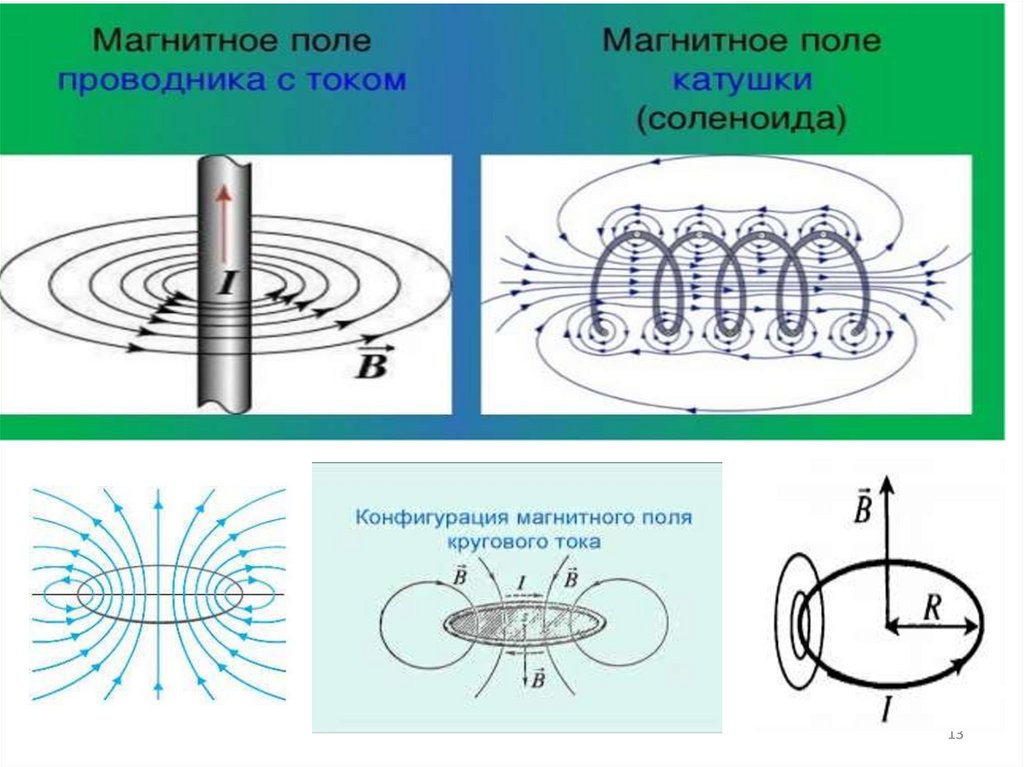
46. Магнитное поле прямого проводника с током

μμ0 I [dl r ]
dB
3
4 r
– магнитная проницаемость изотропной среды;
0 – магнитная постоянная ( 0 = 4 10-7 Гн/м);
r – радиус-вектор, направленный от элемента
проводника к точке, в которой определяется
магнитная индукция поля;
α – угол между радиусом-вектором и направление
м тока в элементе провода.
46

47.

Зако- Савара - Лапласа позволяет рассчитать магнитную индукцию
(и напряженность магнитного поля) проводника с током:
(1)
Здесь dl — вектор элемента проводника с током, направленный в
сторону протекания тока; r — радиус-вектор, проведенный от
элемента dl к точке вычисления индукции. Такое векторное
произведение отвечает правилу правого винта, в соответствии с
которым: если острие винта задаст направление тока, то
направление вращения головки винта дает направление магнитной
индукции.
В скалярном виде Закон Био-Савара-Лапласа
(2)
имеет вид , где ɑ — угол между векторами dl и r.
Закон Био -Савара - Лапласа применительно к магнитному полю в
определенной мере является аналогом закона Кулона для электро47
статики.

48.

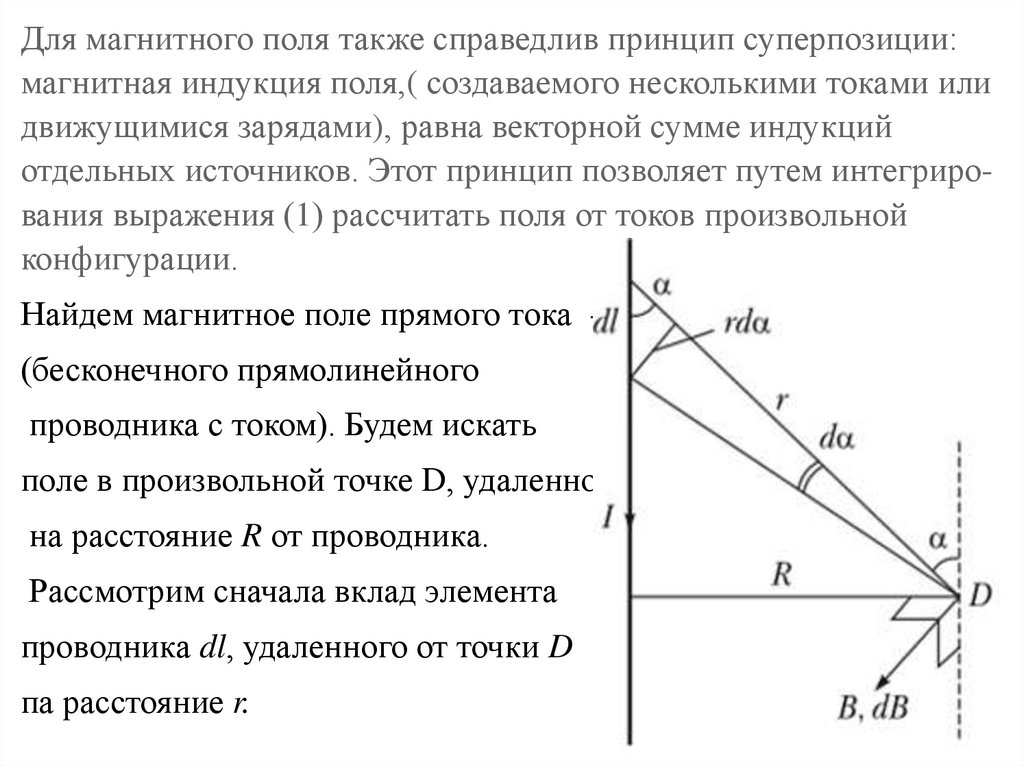
Для магнитного поля также справедлив принцип суперпозиции:
магнитная индукция поля,( создаваемого несколькими токами или
движущимися зарядами), равна векторной сумме индукций
отдельных источников. Этот принцип позволяет путем интегрирования выражения (1) рассчитать поля от токов произвольной
конфигурации.
Найдем магнитное поле прямого тока (бесконечного прямолинейного
проводника с током). Будем искать
поле в произвольной точке D, удаленной
на расстояние R от проводника.
Рассмотрим сначала вклад элемента
проводника dl, удаленного от точки D
па расстояние r.
48

49.

Из определения векторного произведения и формулы (1)
следует, что векторы dB от этого (и любого другого) элемента
имеют одинаковое направление — перпендикулярно плоскости
рисунка. Это означает, что интегрирование уравнения закона БиоСавара - Лапласа можно выполнять в скалярном виде. Из рисунка
очевидно, что
Подставив это выражение в закон
получим
Био-Савара-Лапласа (2),
Проинтегрировав этот выражение по бесконечному проводнику
(угол ɑ изменяется от 0 до π) получим
Таким образом магнитная индукция
магнитного поля прямого тока равна
49

50.

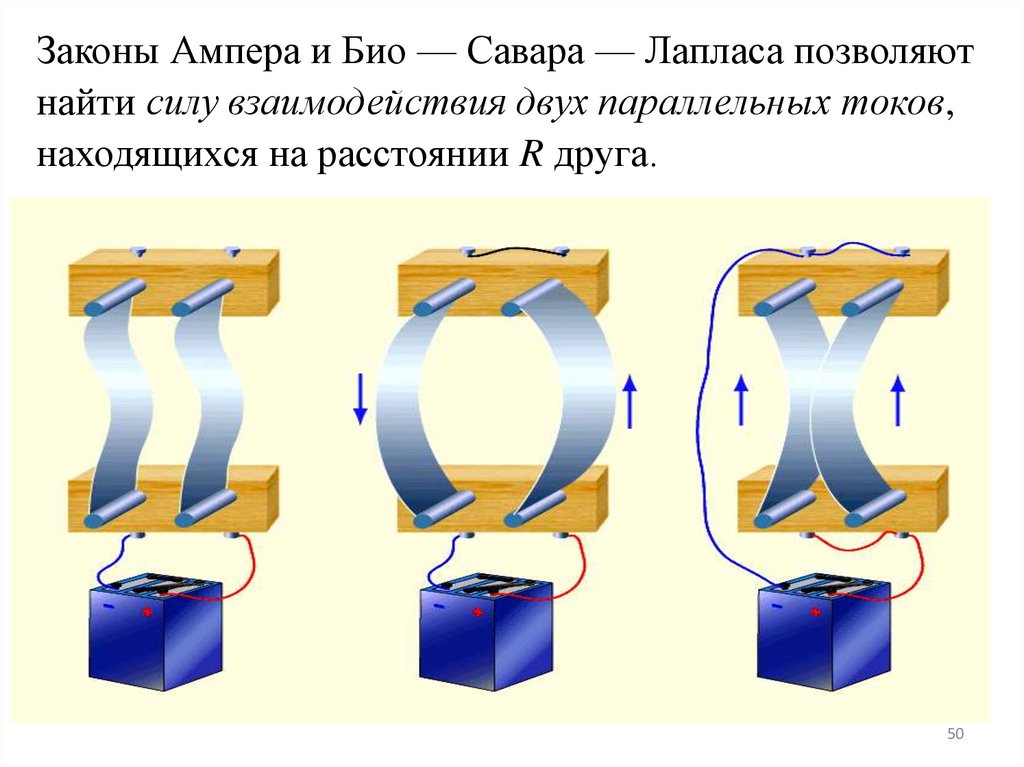
Законы Ампера и Био — Савара — Лапласа позволяют
найти силу взаимодействия двух параллельных токов,
находящихся на расстоянии R друга.
50

51.

51

52.

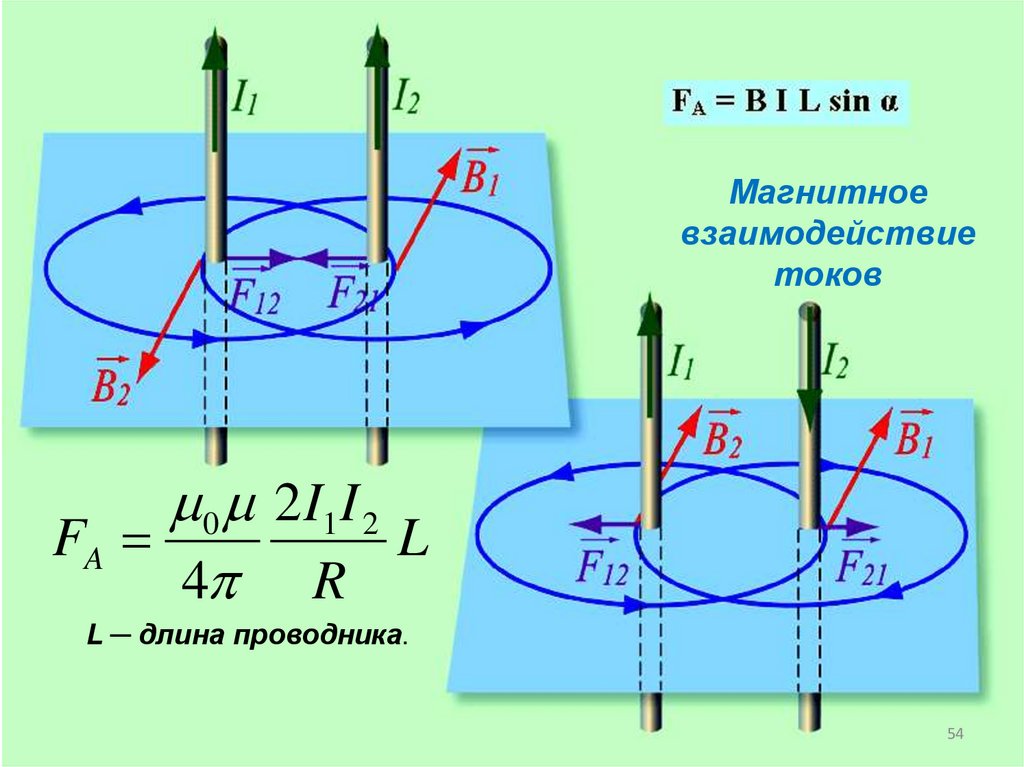
Любой проводник с током создает вокруг себя
магнитное поле. Если поместить в это поле другой
проводник с током, то между этими проводниками
возникают силы взаимодействия. При этом
параллельные сонаправленные токи притягиваются,
противоположно направленные - отталкиваются.
52

53.

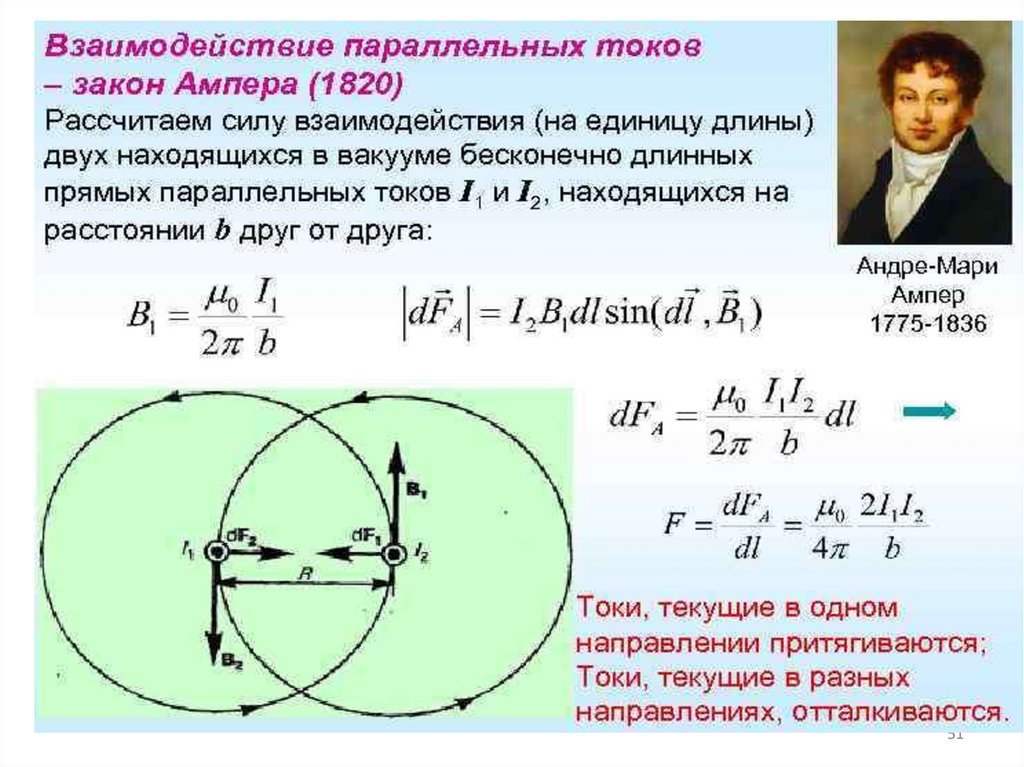
Сила, действующая на единицу длины проводника между двумя бесконечно длинными проводниками с током,
прямо пропорциональна силе тока в каждом из них и
обратно пропорциональна расстоянию между ними.
За единицу силы тока в системе СИ принята такая сила
постоянного тока, который протекая по двум бесконечно
длинным параллельным проводникам бесконечно малого
сечения, расположенным в вакууме на расстоянии 1 м
друг от друга, вызывает силу, действующую на единицу
длины проводника, равную 2·10-7 Н.
где µ = 1; I1 = I2 = 1А ; d = 1 м; µ0 = 4π·10-7 Гн/м – магнит53
ная постоянная..

54.

Магнитное
взаимодействие
токов
0 2 I1 I 2
FA
L
4 R
L ─ длина проводника.
54

55.

Магнитная индукция
1) поля, созданного бесконечно длинным прямым
проводником с током (рис.1) , где r = r0
μμ0 I
B
2 r0
(рис.1)
(рис.2)
2) поля в центре кругового витка с током ( рис.2), где
h=r
2
μμ0 IR
μμ 0 I
B
3
B
2
2 2
2
(
R
h
)
55
2R

56.

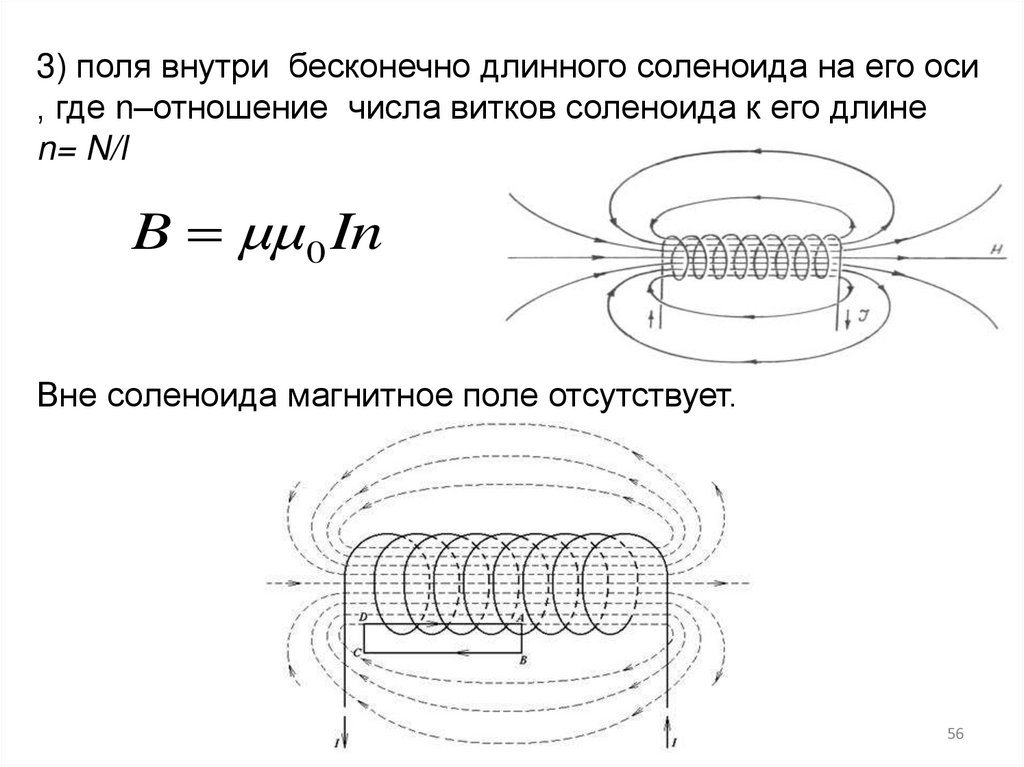
3) поля внутри бесконечно длинного соленоида на его оси
, где n–отношение числа витков соленоида к его длине
n= N/l
B μμ0 In
Вне соленоида магнитное поле отсутствует.
56

57.

5. Поток вектора
магнитной индукции
Потоком вектора магнитной индукции
через элементарную площадку dS называется
физическая величина dФm , равная произведению
величины этой площадки и проекции вектора В
на направление нормали к площадке dS.
57

58.

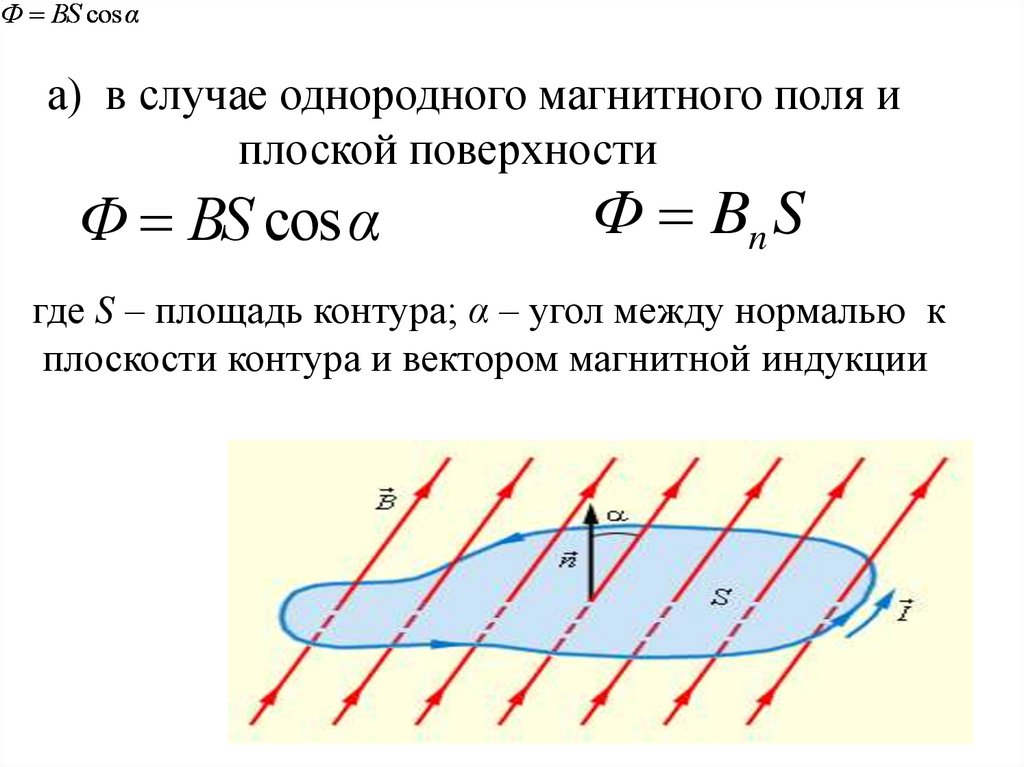
Ф BS cos α
а) в случае однородного магнитного поля и
плоской поверхности
Ф BS cos α
Ф Bn S
где S – площадь контура; α – угол между нормалью к
плоскости контура и вектором магнитной индукции
58

59. б) неоднородного магнитного поля и произволь-ной поверхности

б) неоднородного магнитного поля и произвольной поверхности
• Интегрируя это выражение по S, получим
магнитный поток Фm сквозь произвольную
поверхность S:
Вn =Bcosα
59

60.

ФE En dS
S
1
0
qi
60

61. 6. Работа перемещения проводника с током в магнитном поле

На проводник с током в магнитном поле действует сила, под
действием которой проводник может перемещаться, совершая
работу. Предположим, что электрическая цепь находится в
однородном магнитном поле и прямой проводник АС длиной l ,
входящий в цепь тока, перемещается на расстояние dx и переходит из положения 1 в положение 2.
Магнитное поле В перпендикулярно
к плоскости цепи. На проводник l
действует сила F=IВl и механическая
работа выразится формулой
dA= IBldx = IBdS,
где dS- площадь,
описываемая проводником при его перемещении.
61

62.

Если индукция поля В направлена иначе, то всегда ее можно разложить составляющие - на нормальную к плоскости и касательную.
Работу совершает только нормальная составляющая. Поэтому
можно записать
dA= IBndS= IdФn .
Полагая силу тока постоянной и интегрируя выражение IdФn (3),
получим
A=I ΔФ, т.е. работа силы Ампера при перемещении
проводника конечной длины с постоянным током равна произведению тока на изменение потока магнитной индукции через
площадь контура , очерченную проводником при его движении
в магнитном поле .
• Если работу совершают силы поля, то А 0 и энергия самого поля
убывает.
• Сила Лоренца не совершает работу. Под действием силы Лоренца
меняется только направление скорости заряда.( см слайд 23 этой
лекции)
62

63. Циркуляция вектора В

Отличие магнитного поля от электростатического проявляется
также
в значении величины, которую мы называем циркуляцией — интеграла от векторного поля по замкнутому
пути. В электростатике равен нулю интеграл
взятый по
произвольному замкнутому контуру. Это связано с потенциальностью электростатического поля, то есть с тем фактом, что работа по перемещению заряда в электростатическом поле не зависит
от пути, но только от положения начальной и конечной точек.
Посмотрим, как обстоит дело с аналогичной величиной для магнитного поля. Возьмем замкнутый контур, охватывающий прямой
ток, и вычислим для него циркуляцию вектора В, то есть
Как было получено выше, магнитная индукция В, создаваемая
прямолинейным проводником с током на расстоянии R от проводника равна
63

64.

Рассмотрим случай, когда контур, охватывающий прямой ток,
лежит в плоскости, перпендикулярной току, и представляет собой
окружность радиусом R с центром на проводнике. В этом случае
циркуляция вектора В по этой окружности равна
откуда
В силу принципа суперпозиции циркуляция вектора магнитной
индукции по пути, охватывающем несколько токов,
пропорциональна их алгебраической сумме .
Циркуляция вектора магнитной индукции
отлична от нуля, если контур, по которому
она берется, охватывает ток.
64

65.

Так сумма токов на рисунке равна I1+ 2I2 + 0 - I4
65

66.

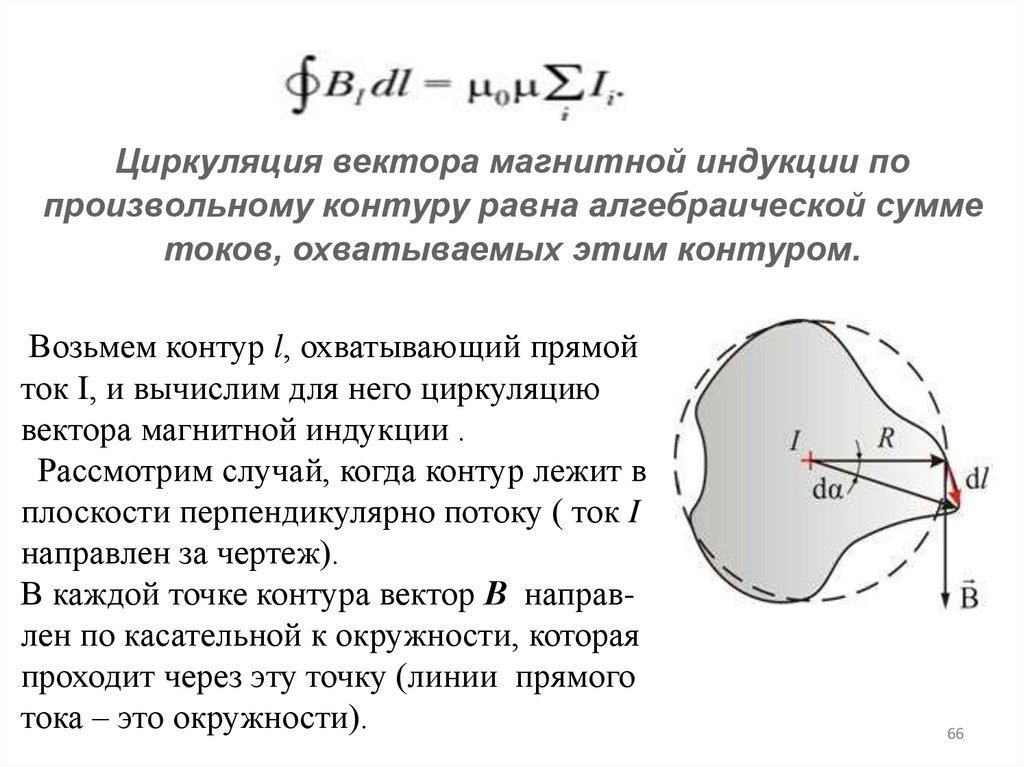
Циркуляция вектора магнитной индукции по
произвольному контуру равна алгебраической сумме
токов, охватываемых этим контуром.
Возьмем контур l, охватывающий прямой
ток I, и вычислим для него циркуляцию
вектора магнитной индукции .
Рассмотрим случай, когда контур лежит в
плоскости перпендикулярно потоку ( ток I
направлен за чертеж).
В каждой точке контура вектор В направлен по касательной к окружности, которая
проходит через эту точку (линии прямого
тока – это окружности).
66

67.

Использем свойства скалярного произведения векторов.
где
Но
-проекция dl на вектор В .
, где R- расстояние от прямой тока I до dl .
67

68.

Напряженность магнитного поля
соленоида.
Применим теорему о циркуляции В для вычисления напряженности магнитного поля длинного соленоида с током I.
Искусство применения теоремы о циркуляции зависит от
выбора удобного для расчета контура.
. Соленоид — это провод, равномерно
навитый на цилиндрический каркас.
Будем считать, что диаметр каркаса
много меньше его длины, а шаг
плотной намотки (расстояние между
витками) много меньше диаметра.
При этих условиях поле внутри
соленоида будет однородным, а поле вне соленоида можно
считать равным нулю. Из соображений симметрии поле внутри
соленоида направлено вдоль оси соленоида. Пусть плотность
намотки витков (число витков на единицу длины)
n= N / l .68

69.

Возьмем прямоугольный контур 1-2-3-4 и вычислим циркуляцию
вектора В по этому контуру.
Второй и четвертый интегралы равны
нулю в силу перпендикулярности
векторов
и
(B dl cos90). Третий интеграл можно положить
равным нулю, ввиду малости магнитного поля вне соленоида.
Поэтому
Рассмотренный контур охватывает суммарный ток nI, где n - число
витков соленоида, приходящееся на единицу длины, I - сила тока
в соленоиде.
или
B= µ0 I n .
69