ЛЕКЦИЯ 5

1.

1

2.

2

3.

3

4.

Электростатика
– раздел электродинамики,
изучающий взаимодействие
неподвижных зарядов.
4

5.

Электрический заряд
- физическая величина
характеризующая свойство тел
или частиц вступать в
электромагнитные взаимодействия и
определяющая значения сил и энергий
при таких взаимодействиях.
5

6. Свойства электрических зарядов

Электрический заряд
cуществует в двух видах:
Положительный
Отрицательный
Электрический заряд и н в а р и а н т е н
(его величина не зависит от системы отсчета, т. е. от того,
движется он или покоится).
Электрический заряд д и с к р е т е н,
т. е. заряд любого тела составляет целое кратное
элементарного электрического заряда е.
Электрический заряд а д д и т и в е н
(заряд любой системы частиц (тел) равен сумме зарядов
частиц (тел ), входящих в систему).
Электрический заряд замкнутой системы тел п о с т о я н е н6.

7.

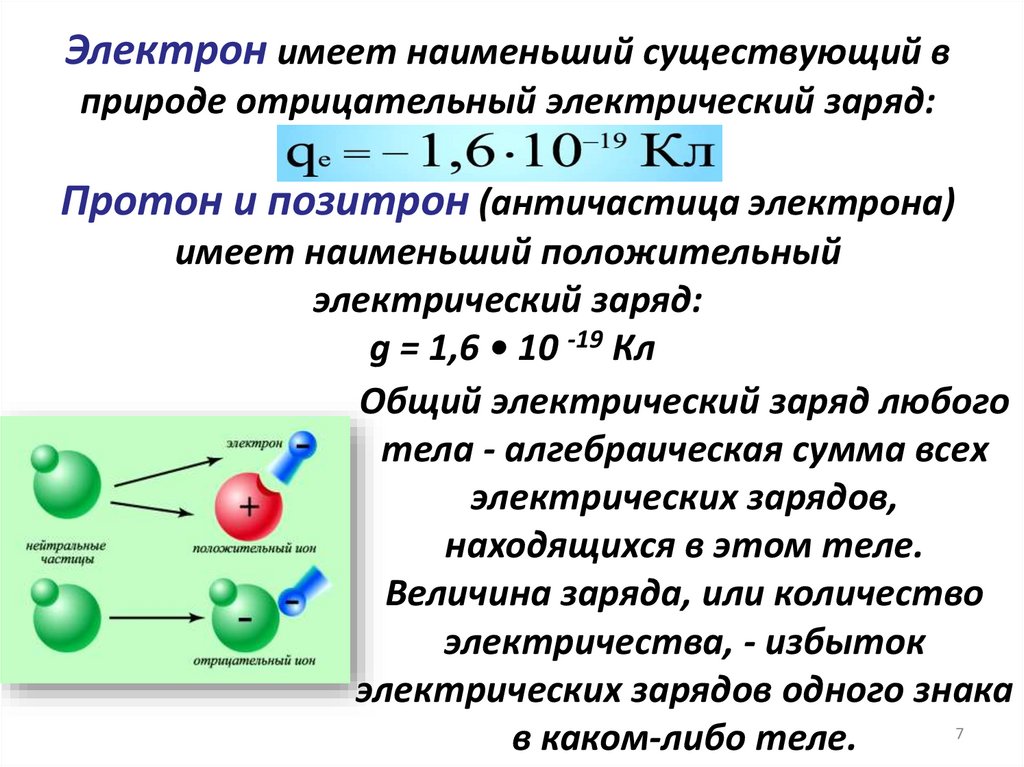
Электрон имеет наименьший существующий в
природе отрицательный электрический заряд:
g = e = - 1,6 • 10 -19 Кл
Протон и позитрон (античастица электрона)
имеет наименьший положительный
электрический заряд:
g = 1,6 • 10 -19 Кл
Общий электрический заряд любого
тела - алгебраическая сумма всех
электрических зарядов,
находящихся в этом теле.
Величина заряда, или количество
электричества, - избыток
электрических зарядов одного знака
7
в каком-либо теле.

8. Закон сохранения электрического заряда

- физический закон, в соответствии с которым
в замкнутой системе взаимодействующих
тел алгебраическая сумма электрических
зарядов (полный электрический заряд)
остается неизменной при всех
взаимодействиях.
8

9. Закон Кулона

Закон Кулона - основной закон
электростатики, выражающий
зависимость силы взаимодействия
двух неподвижных точечных зарядов
от расстояния между ними.
Дает возможность определить силу
взаимодействия между
неподвижными заряженными телами.
Справедлив только для точечных
зарядов.
Точечным называется заряд
сосредоточенный на теле,
линейные размеры которого
значительно меньше расстояния
до других заряженных тел.
9

10.

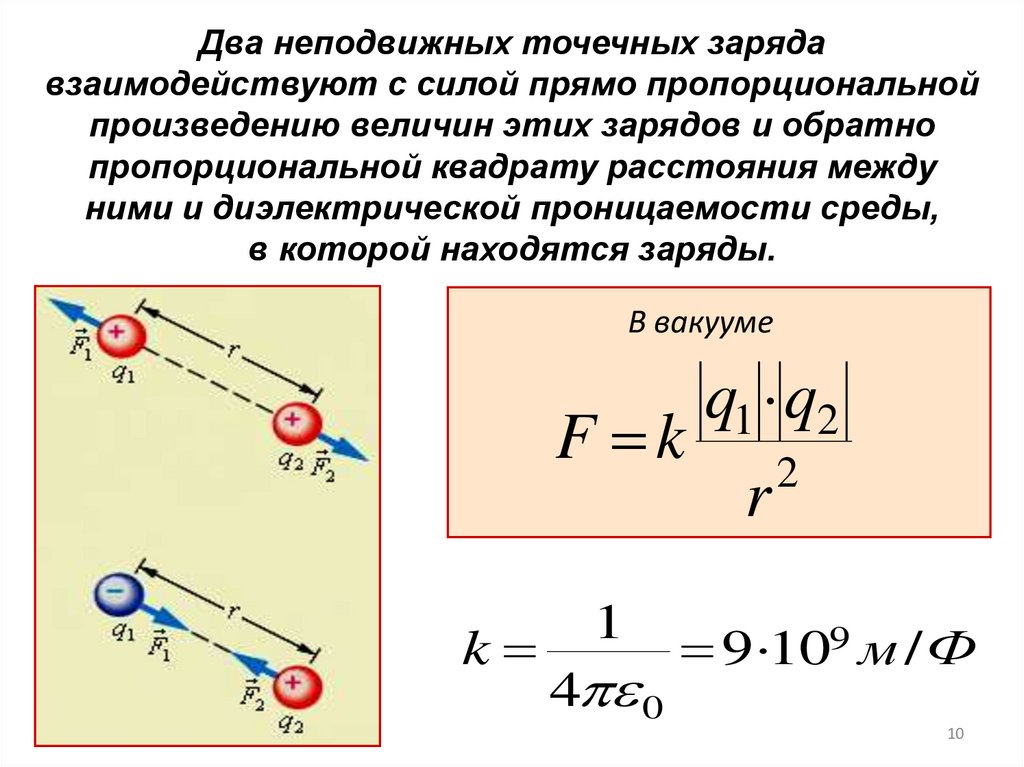
Два неподвижных точечных заряда
взаимодействуют с силой прямо пропорциональной
произведению величин этих зарядов и обратно
пропорциональной квадрату расстояния между
ними и диэлектрической проницаемости среды,
в которой находятся заряды.
В вакууме
q1 q2
F k 2
r
k
1
4 0
9 109 м / Ф
10

11.

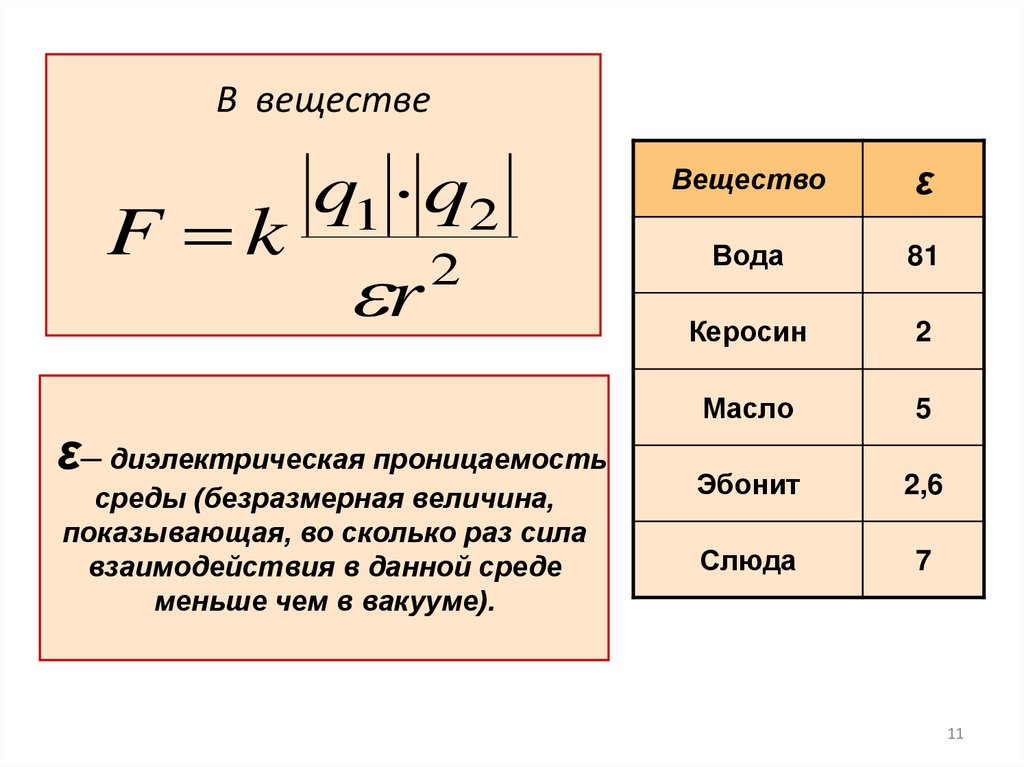
В веществе
q1 q2
F k
2
r
ε─ диэлектрическая проницаемость
среды (безразмерная величина,
показывающая, во сколько раз сила
взаимодействия в данной среде
меньше чем в вакууме).
Вещество
ε
Вода
81
Керосин
2
Масло
5
Эбонит
2,6
Слюда
7
11

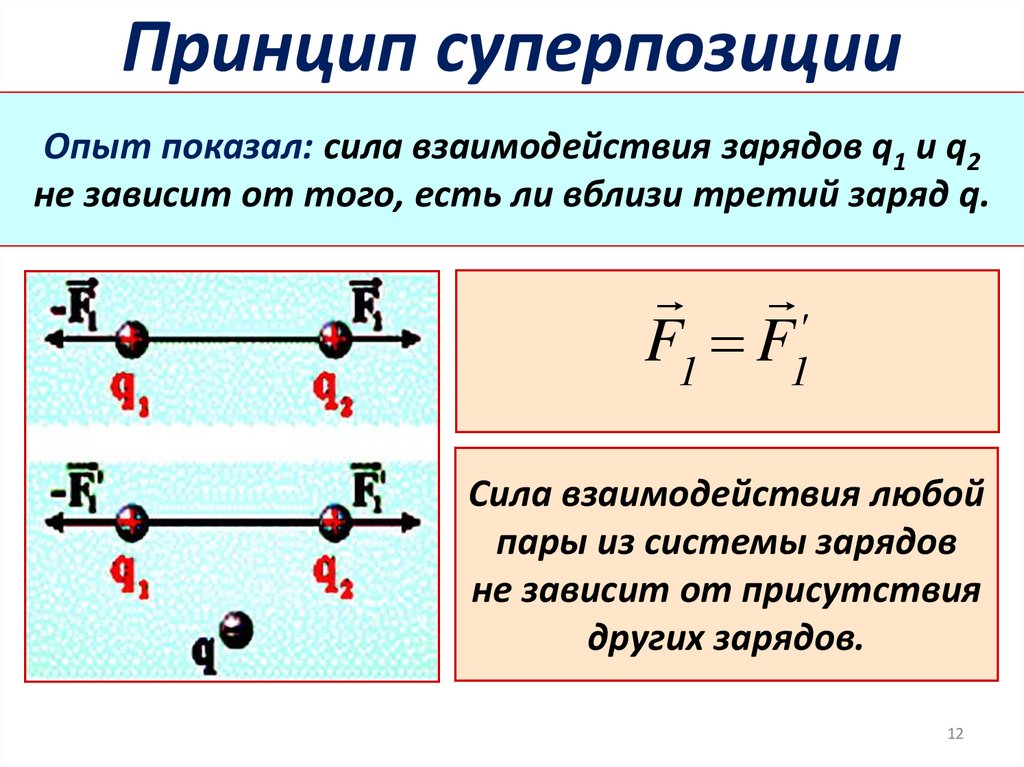
12. Принцип суперпозиции

Опыт показал: сила взаимодействия зарядов q1 и q2
не зависит от того, eсть ли вблизи третий заряд q.
F1 F1'
Сила взаимодействия любой
пары из системы зарядов
не зависит от присутствия
других зарядов.
12

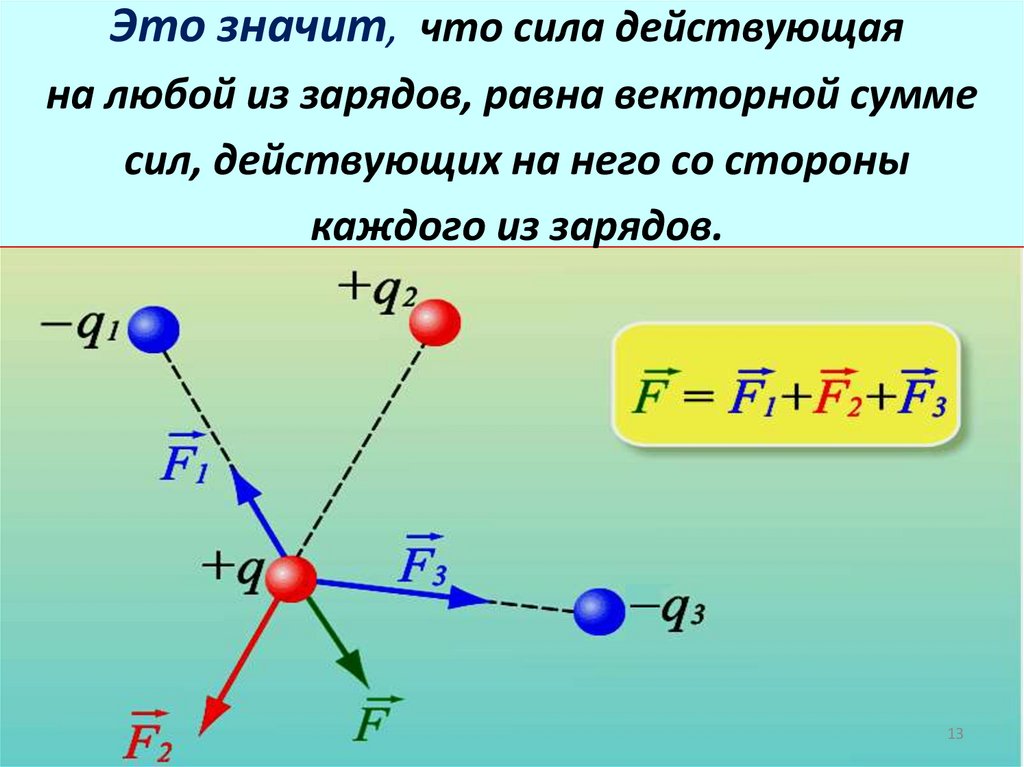
13.

Это значит, что сила действующая
на любой из зарядов, равна векторной сумме
сил, действующих на него со стороны
каждого из зарядов.
13

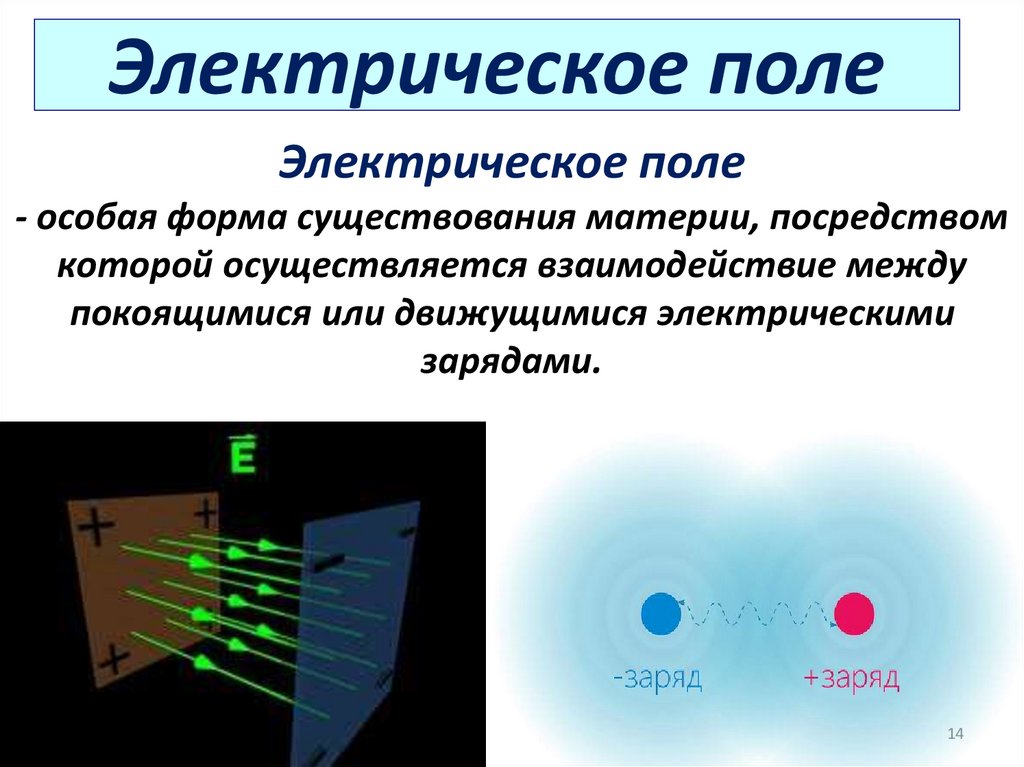
14. Электрическое поле

Электрическое поле
- особая форма существования материи, посредством
которой осуществляется взаимодействие между
покоящимися или движущимися электрическими
зарядами.
14

15.

Заряд является источником
электромагнитного взаимодействия,
или источником электромагнитного поля,
распространяющемся в пространстве со
скоростью света.
15

16.

Электрический заряд q вносит изменение
в окружающее пространство.
На заряды, внесенные в это
пространство, действует сила.
Вокруг любого заряда образуется и
распространяется электрическое поле.
16

17.

Электрическое поле
– силовое поле, посредством которого
взаимодействуют электрические заряды.
Электрическое поле, созданное
неподвижными зарядами, называется
электростатическим.
Небольшой по величине положительный
точечный заряд, используемый
для обнаружения и исследования
электростатического поля,
называется пробным зарядом.
Обозначается q.
17

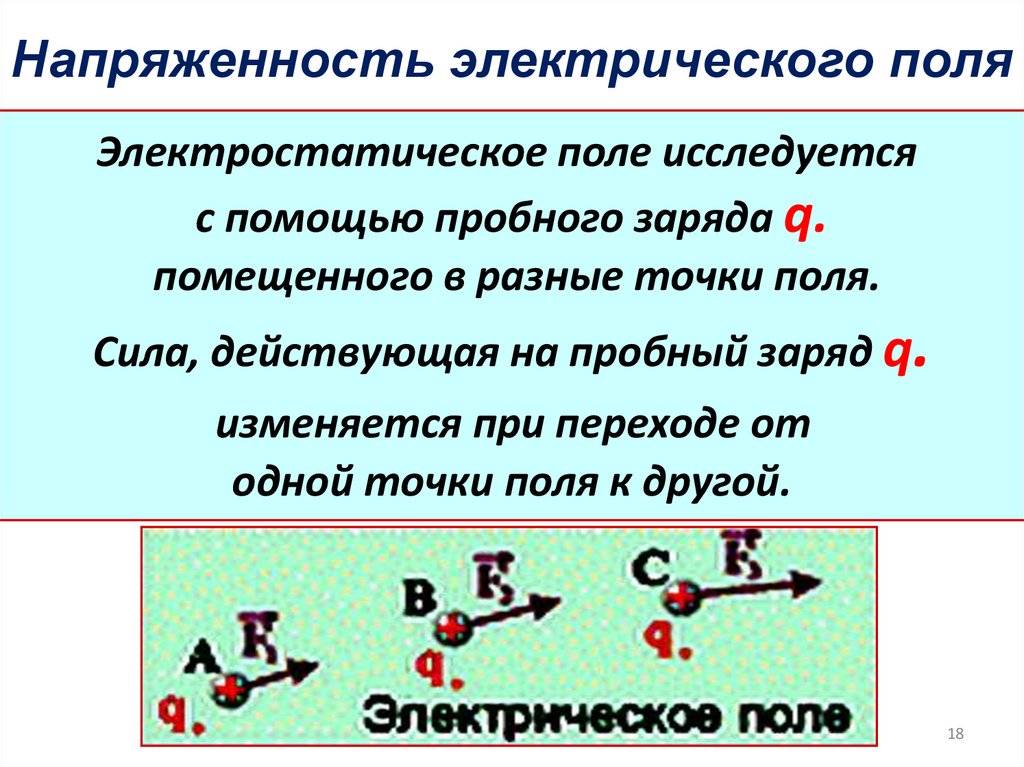
18. Напряженность электрического поля

Электростатическое поле исследуется
с помощью пробного заряда q.
помещенного в разные точки поля.
Сила, действующая на пробный заряд q.
изменяется при переходе от
одной точки поля к другой.
18

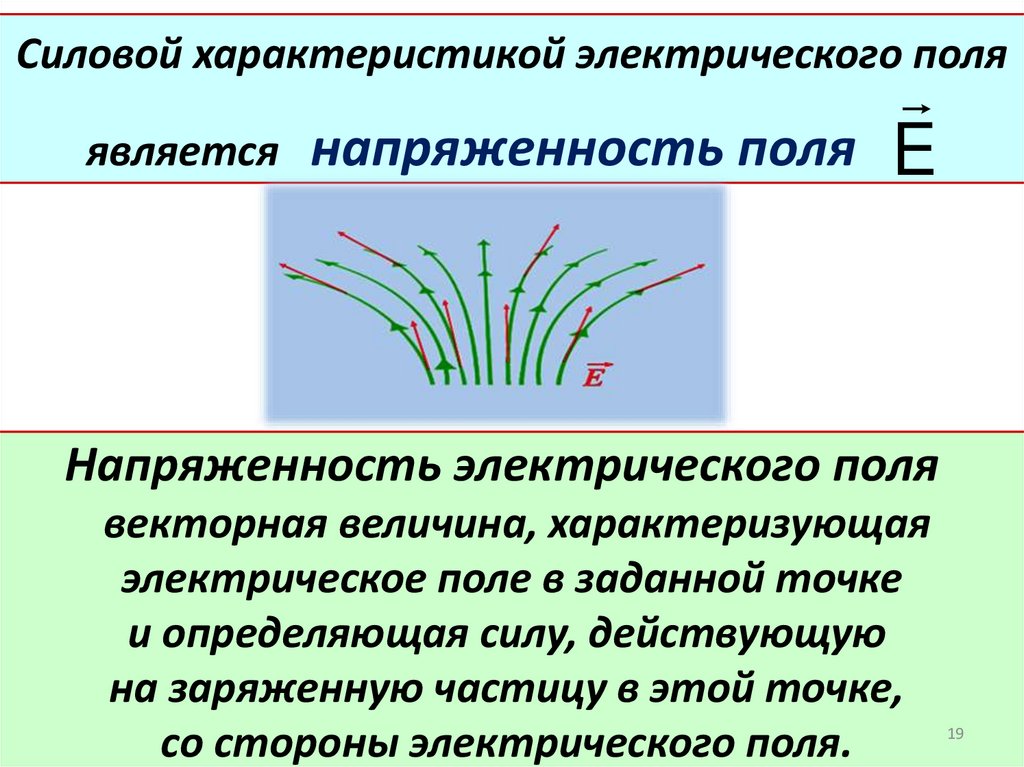
19. Силовой характеристикой электрического поля является напряженность поля

E
Напряженность электрического поля
векторная величина, характеризующая
электрическое поле в заданной точке
и определяющая силу, действующую
на заряженную частицу в этой точке,
со стороны электрического поля.
19

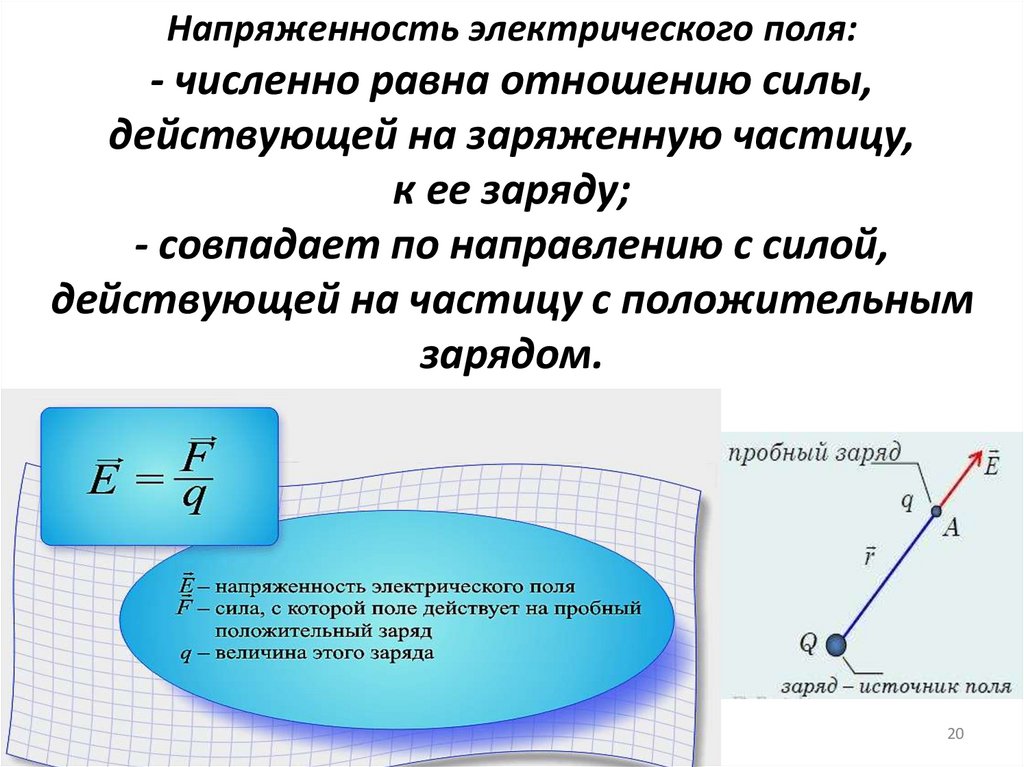
20.

Напряженность электрического поля:
- численно равна отношению силы,
действующей на заряженную частицу,
к ее заряду;
- совпадает по направлению с силой,
действующей на частицу с положительным
зарядом.
20

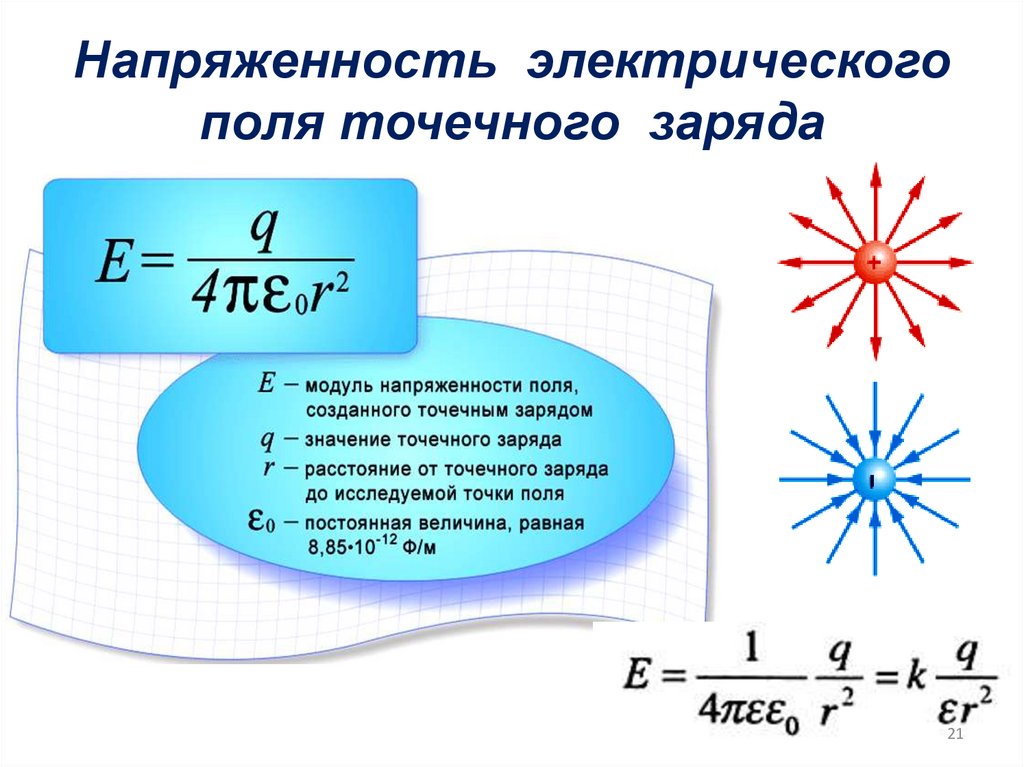
21. Напряженность электрического поля точечного заряда

21

22.

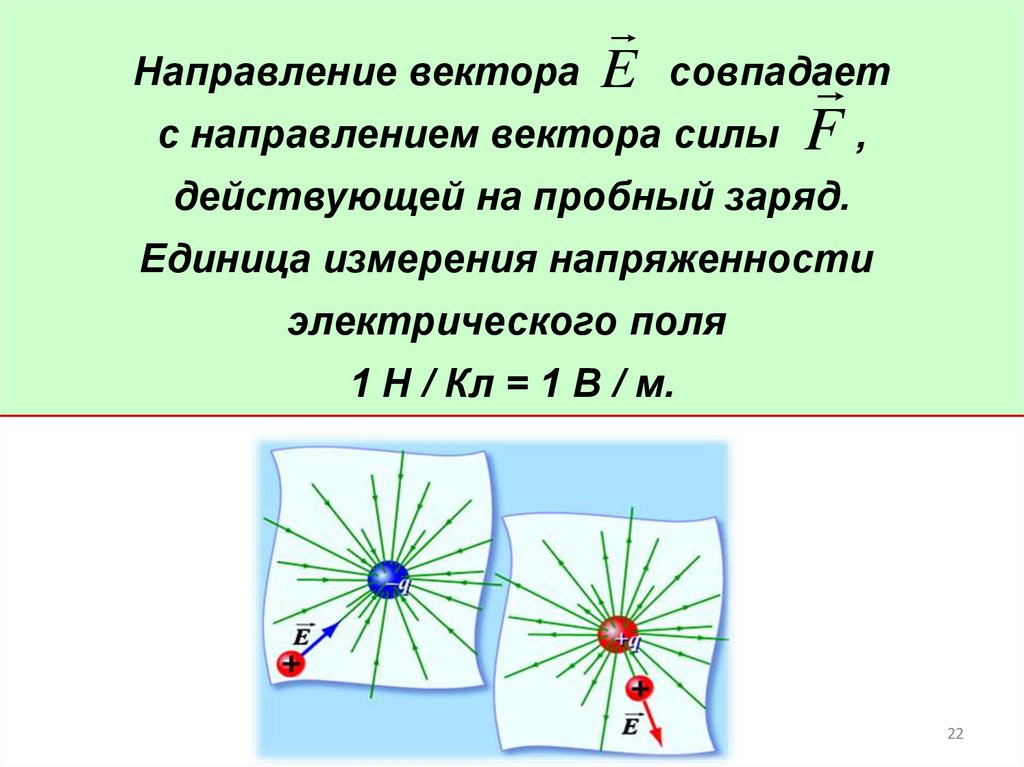
Направление вектора E совпадает
с направлением вектора силы F ,
действующей на пробный заряд.
Единица измерения напряженности
электрического поля
1 Н / Кл = 1 В / м.
22

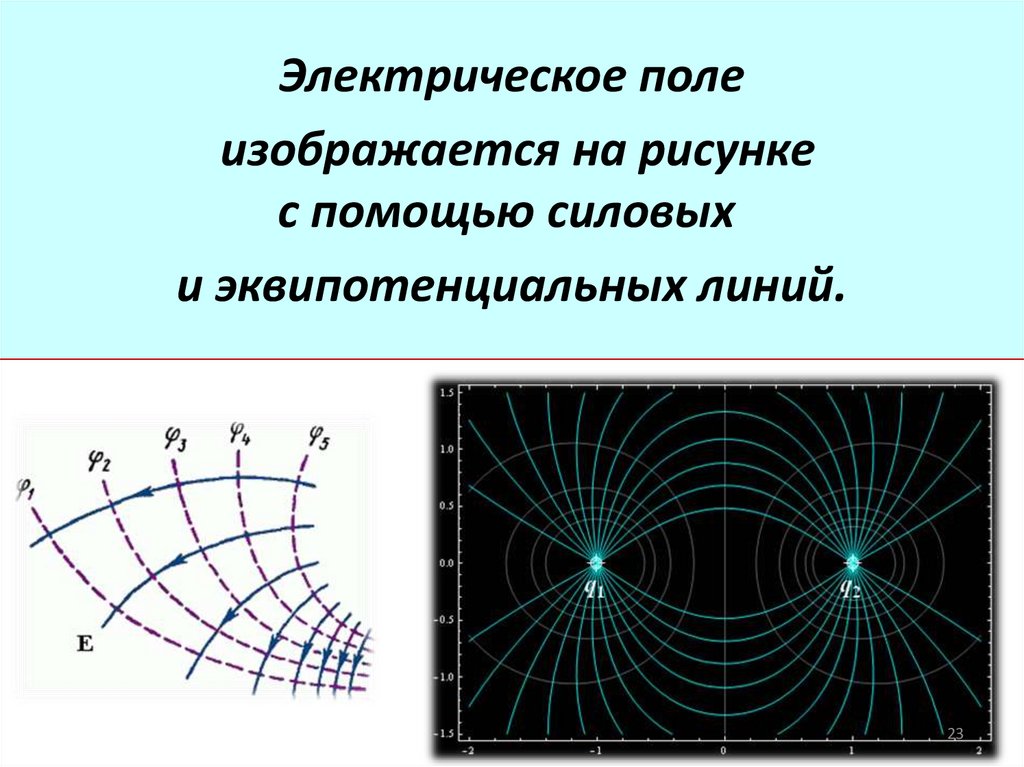
23.

Электрическое поле
изображается на рисунке
с помощью силовых
и эквипотенциальных линий.
23

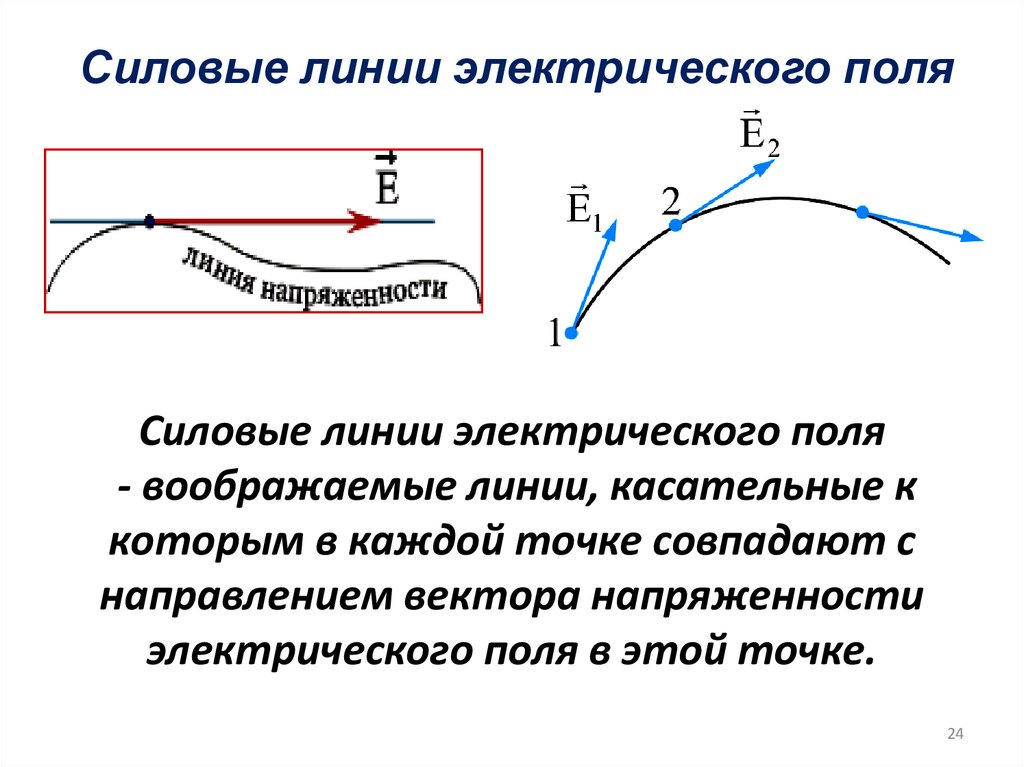
24. Силовые линии электрического поля

Силовые линии электрического поля
- воображаемые линии, касательные к
которым в каждой точке совпадают с
направлением вектора напряженности
электрического поля в этой точке.
24

25.

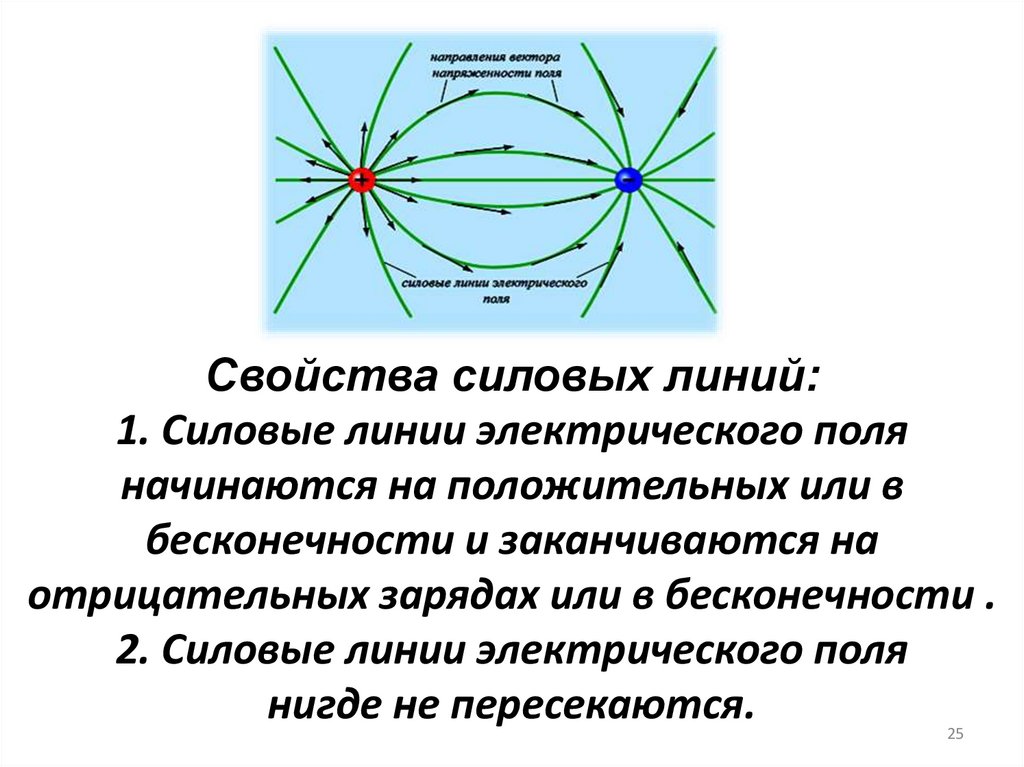
Свойства силовых линий:
1. Силовые линии электрического поля
начинаются на положительных или в
бесконечности и заканчиваются на
отрицательных зарядах или в бесконечности .
2. Силовые линии электрического поля
нигде не пересекаются.
25

26.

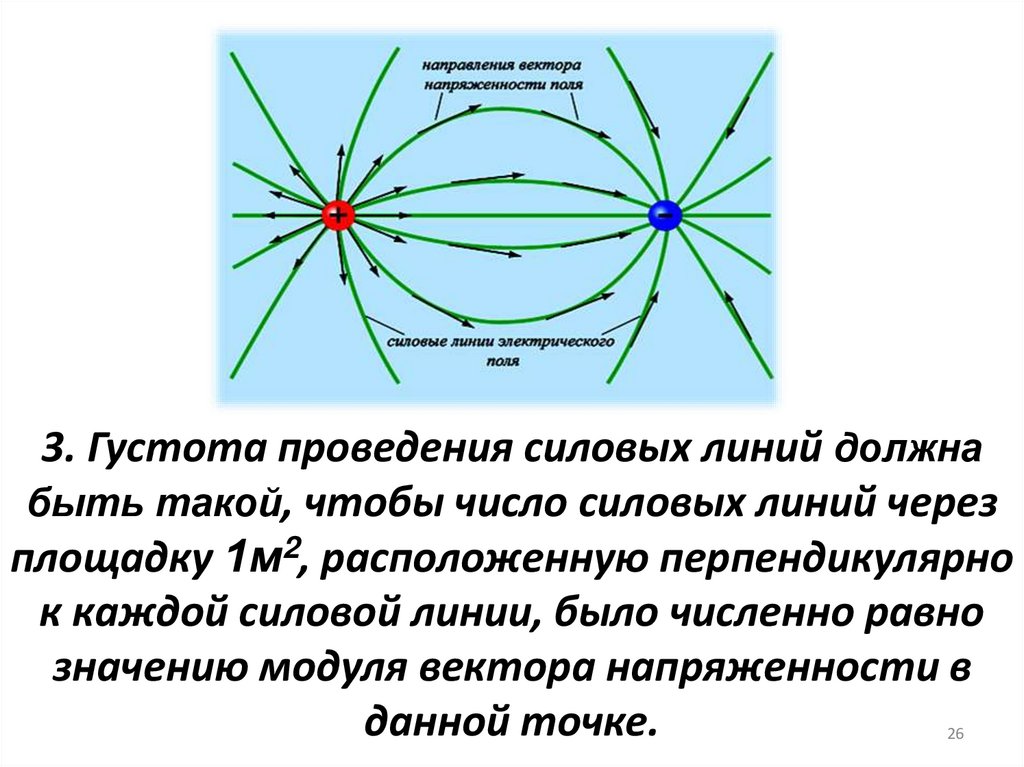
3. Густота проведения силовых линий должна
быть такой, чтобы число силовых линий через
площадку 1м2, расположенную перпендикулярно
к каждой силовой линии, было численно равно
значению модуля вектора напряженности в
данной точке.
26

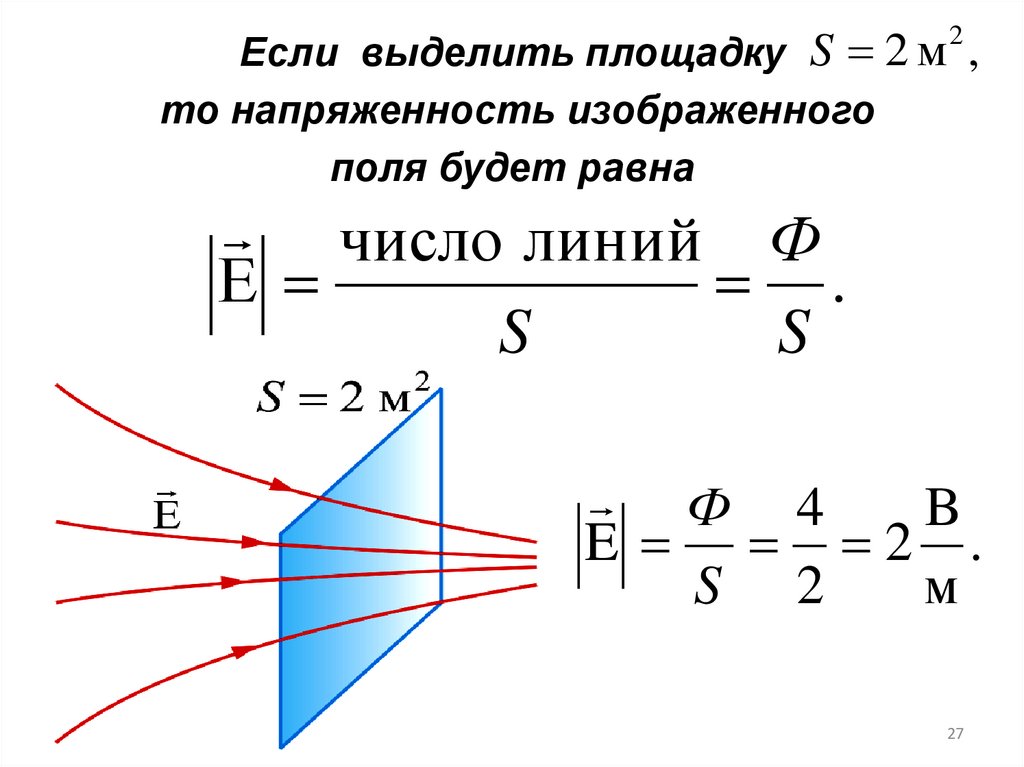
27.

Если выделить площадку S 2 м ,
то напряженность изображенного
поля будет равна
2
число линий Ф
Е
.
S
S
Ф 4
B
E 2 .
S 2
м
27

28.

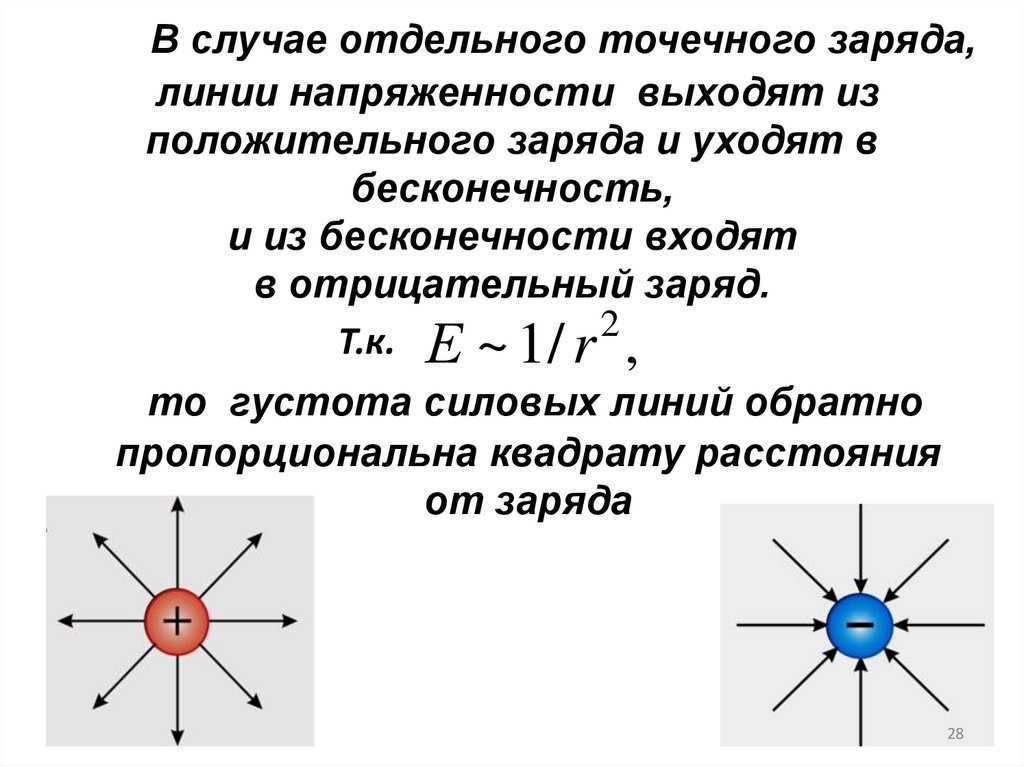
В случае отдельного точечного заряда,
линии напряженности выходят из
положительного заряда и уходят в
бесконечность,
и из бесконечности входят
в отрицательный заряд.
Т.к. Е ~ 1 / r 2 ,
то густота силовых линий обратно
пропорциональна квадрату расстояния
от заряда
28

29.

Однородным называется
электростатическое поле, во всех точках
которого напряженность одинакова по
величине и направлению.
Однородное электростатическое поле
изображается параллельными силовыми
линиями на равном расстоянии друг от
друга.
29

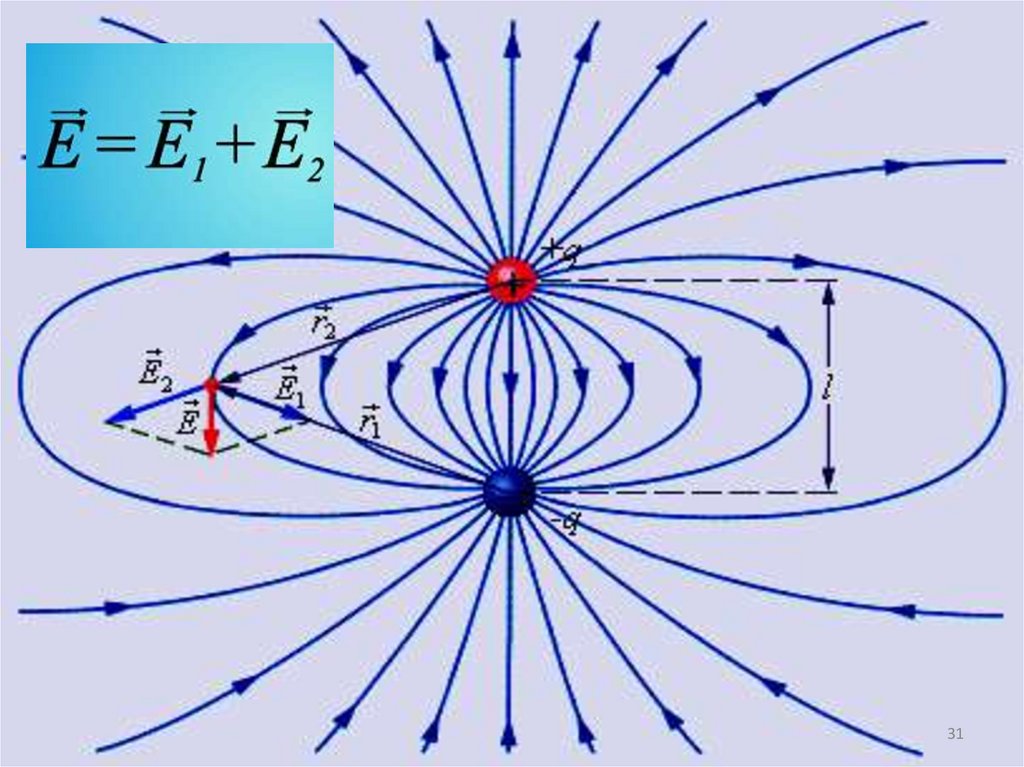
30. если поле создается несколькими зарядами, то напряженность Е в какой-либо точке поля равна векторной сумме напряженностей

Принцип суперпозиции
(наложения) полей
если поле создается несколькими зарядами,
то напряженность Е в какой-либо точке поля
равна векторной сумме напряженностей полей,
созданных в этой точке каждым зарядом
в отдельности.
30

31.

31

32.

Поток вектора напряженности
электрического поля
Число силовых линий сквозь
площадку S, перпендикулярную к ним,
определяет поток вектора сквозь
эту площадку.
Рассмотрим поток вектора Е сквозь
элементарную площадку dS (ΔS)
( в пределах площадки dS
– поле однородное)
32

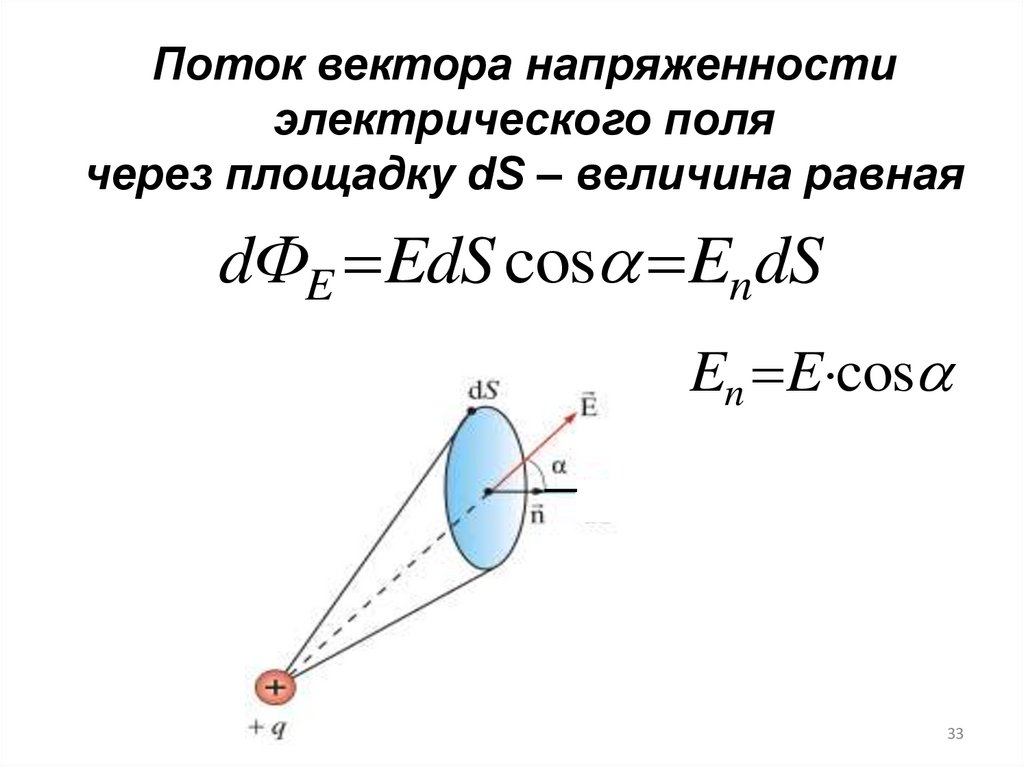
33.

Поток вектора напряженности
электрического поля
через площадку dS – величина равная
dФE EdS cos EndS
En E cos
33

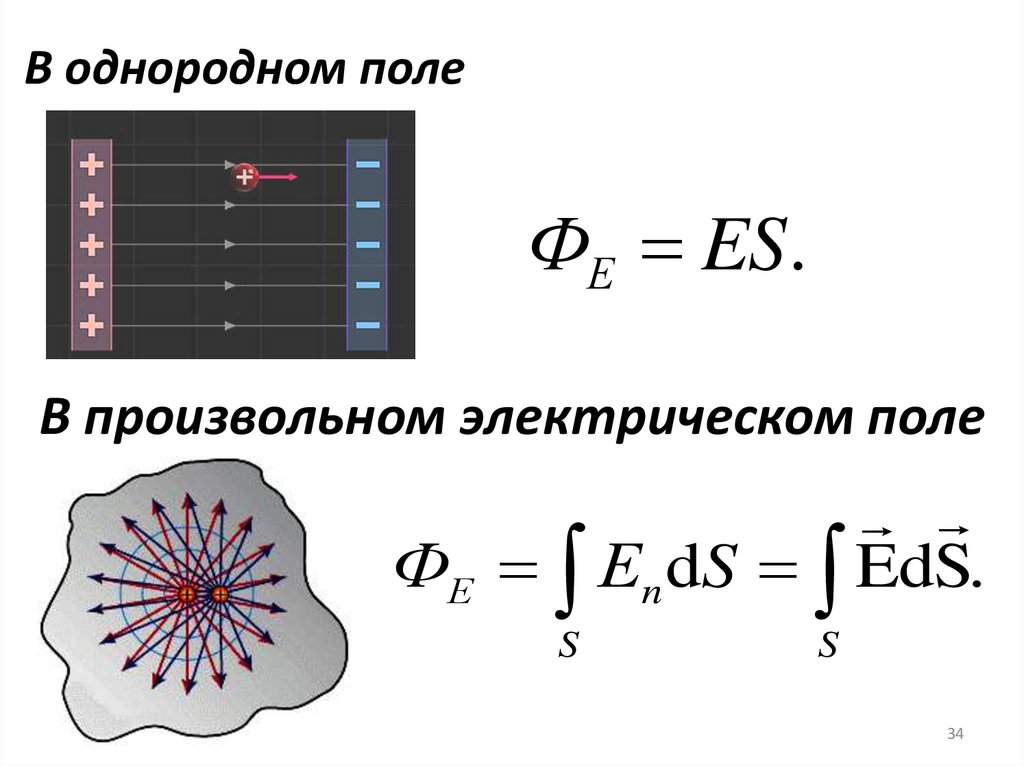
34.

В однородном поле
ФЕ ES.
В произвольном электрическом поле
ФЕ Еn dS EdS.
S
S
34

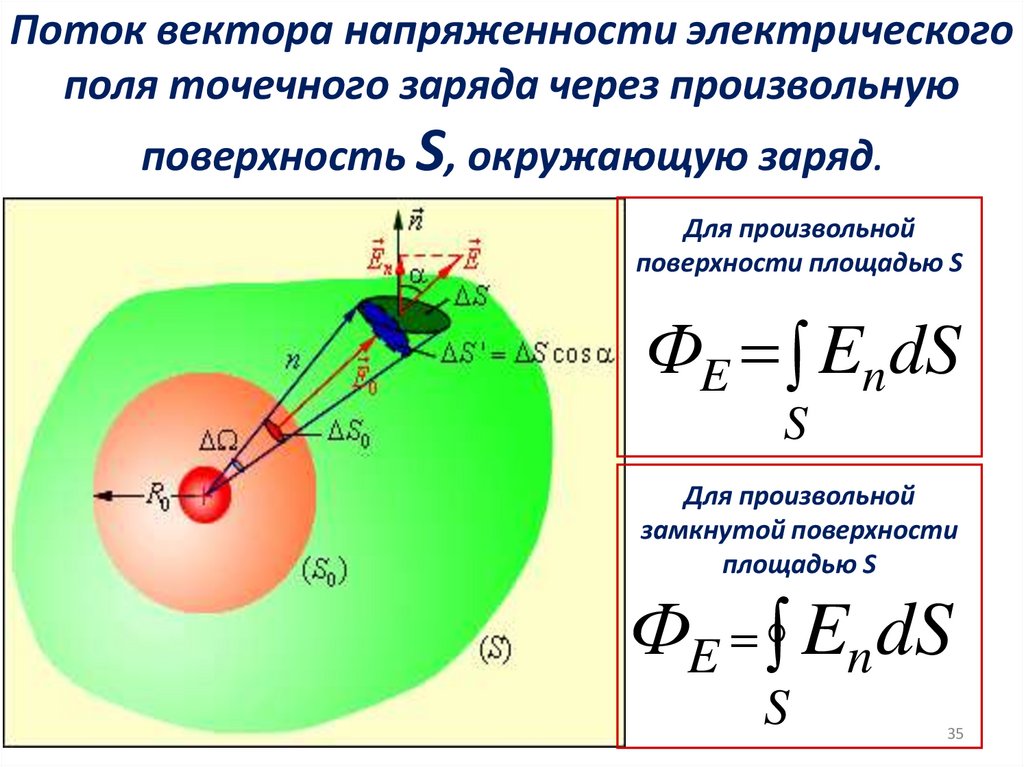
35. Поток вектора напряженности электрического поля точечного заряда через произвольную поверхность S, окружающую заряд.

Для произвольной
поверхности площадью S
ФE En dS
S
Для произвольной
замкнутой поверхности
площадью S
ФE En dS
S
35

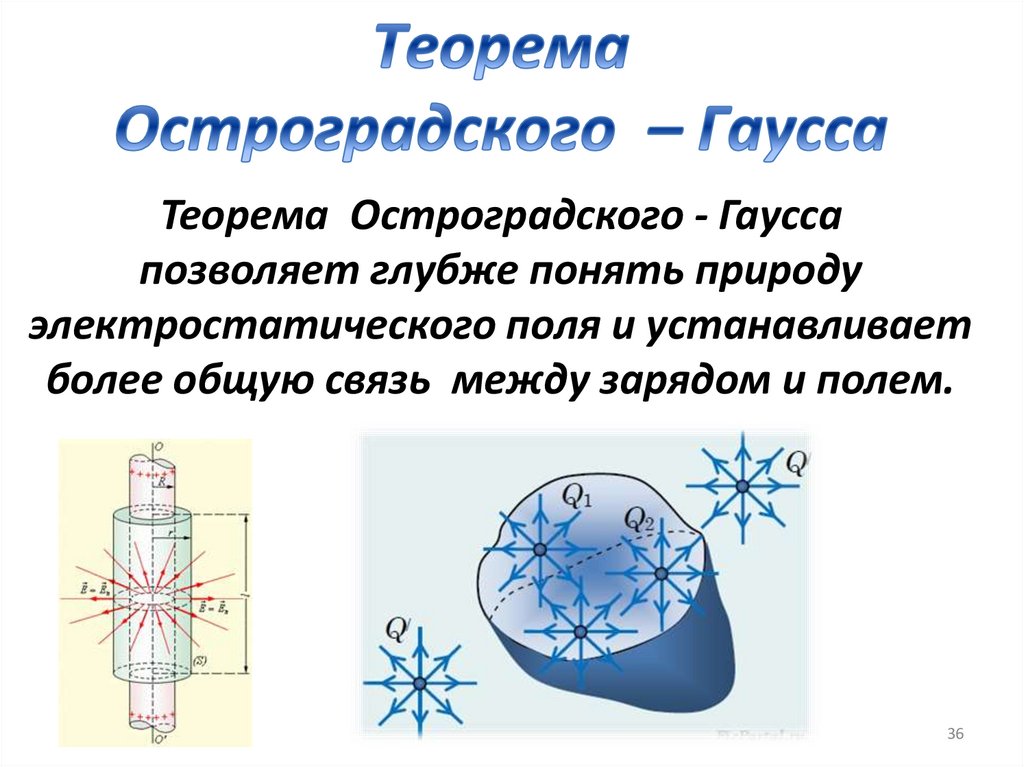
36.

Теорема Остроградского - Гаусса
позволяет глубже понять природу
электростатического поля и устанавливает
более общую связь между зарядом и полем.
36

37. Теорема Остроградского – Гаусса

Поток вектора напряженности
электрического поля
через произвольную замкнутую
поверхность равен алгебраической
сумме зарядов, охваченных
этой поверхностью,
деленной на ε0 .
ФE En dS
S
1
0
qi
37

38. При использовании теоремы Остроградского – Гаусса для расчета электростатических полей нужно:

выбрать замкнутую поверхность, удобную для
данного случая и проходящую через
рассматриваемую точку;
вычислить ФЕ через эту замкнутую поверхность;
вычислить алгебраическую сумму зарядов внутри
выбранной замкнутой поверхности;
подставить полученные выражения в теорему и
вывести формулу, по которой можно рассчитать
напряженность.
38

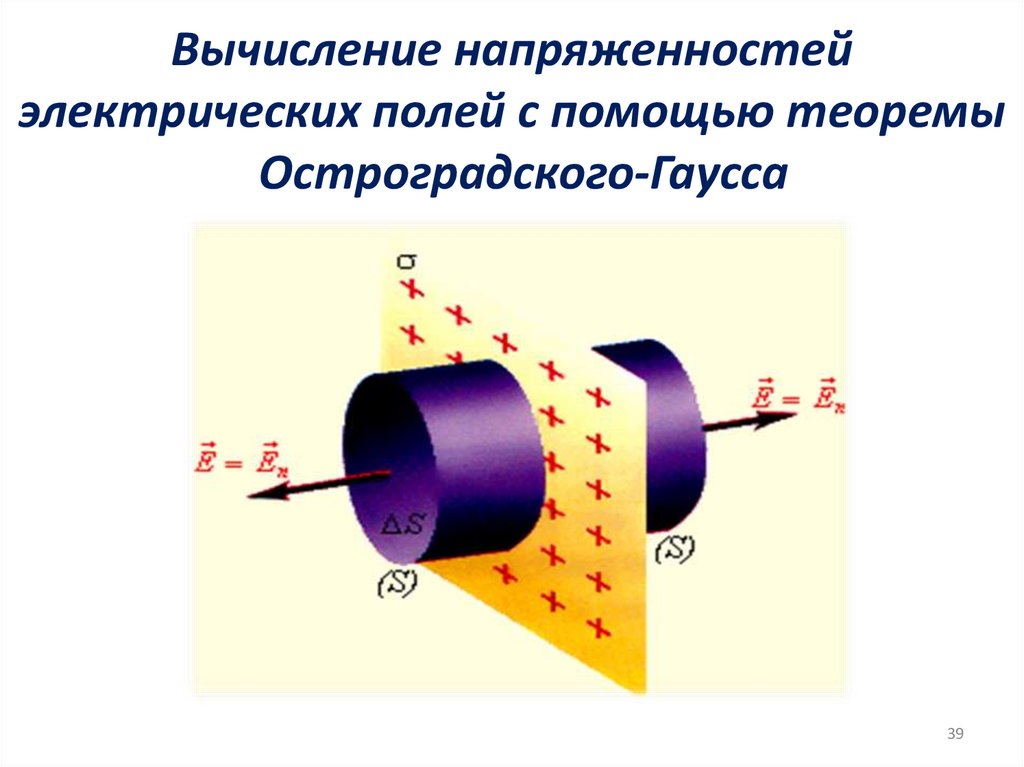
39. Вычисление напряженностей электрических полей с помощью теоремы Остроградского-Гаусса

39

40.

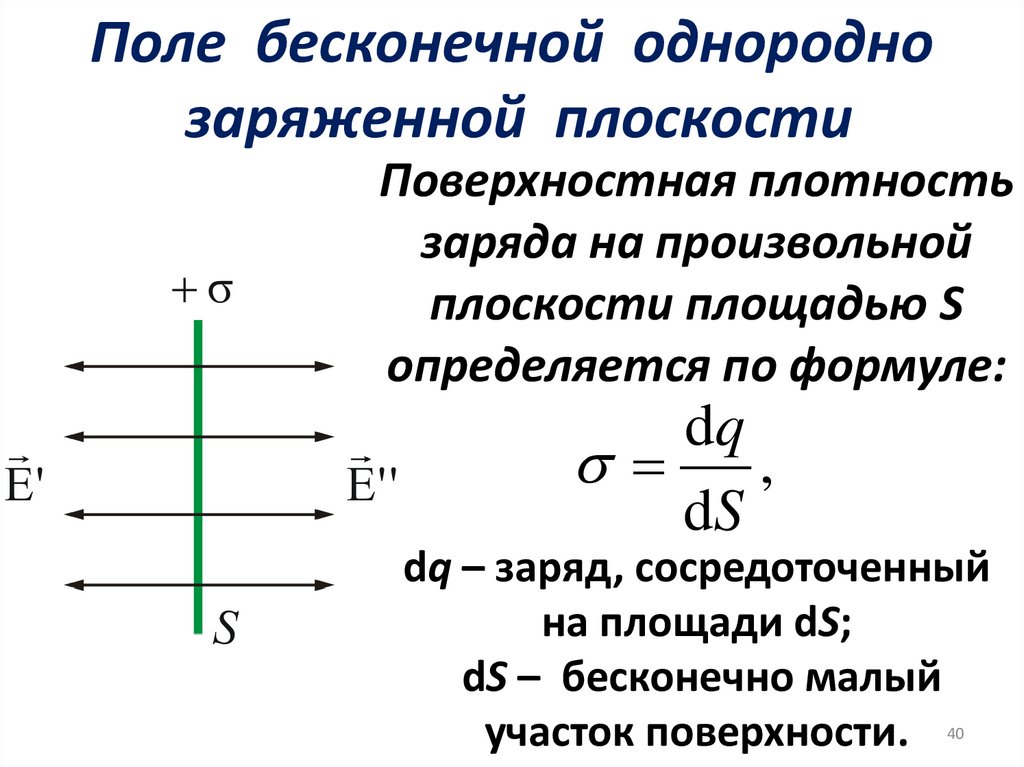
Поле бесконечной однородно
заряженной плоскости
Поверхностная плотность
заряда на произвольной
плоскости площадью S
определяется по формуле:
dq
,
dS
dq – заряд, сосредоточенный
на площади dS;
dS – бесконечно малый
участок поверхности.
40

41.

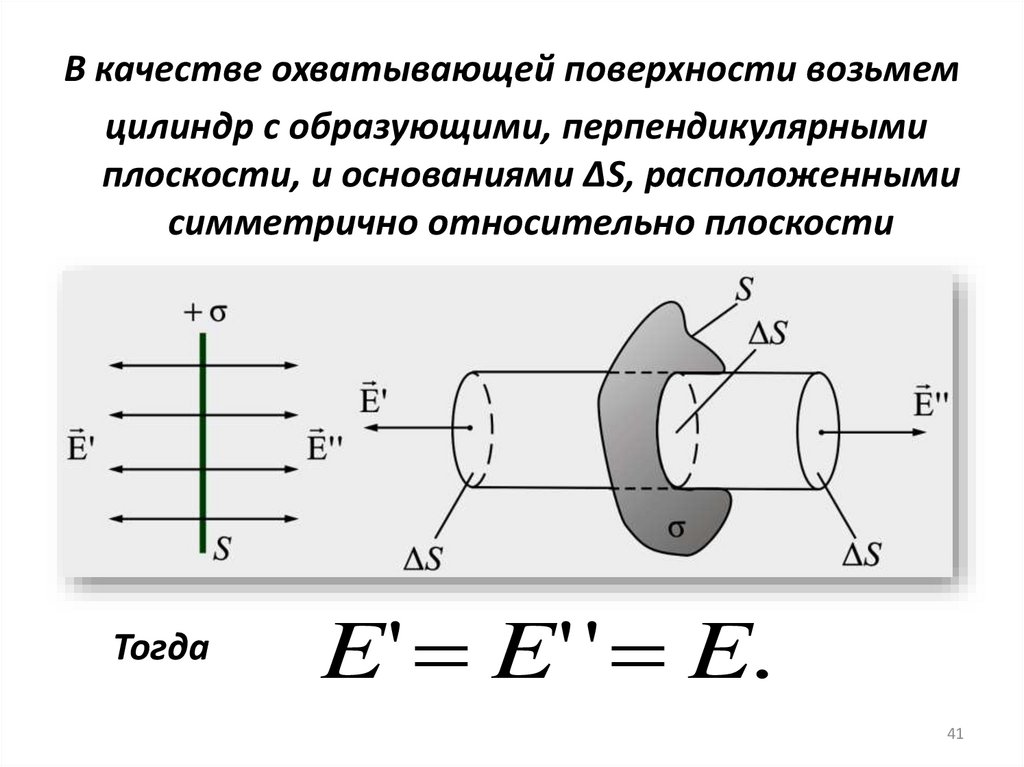
В качестве охватывающей поверхности возьмем
цилиндр с образующими, перпендикулярными
плоскости, и основаниями ΔS, расположенными
симметрично относительно плоскости
Тогда
E' E' ' E.
41

42.

Суммарный поток через замкнутую поверхность
(цилиндр) будет равен:
ФЕ 2 SE.
Внутри поверхности заключен заряд .
Следовательно, из теоремы
Остроградского - Гаусса получим:
ФЕ
q
0
2 SE S
1
0
откуда видно, что напряженность поля
плоскости S равна:
E
.
2 0
42

43.

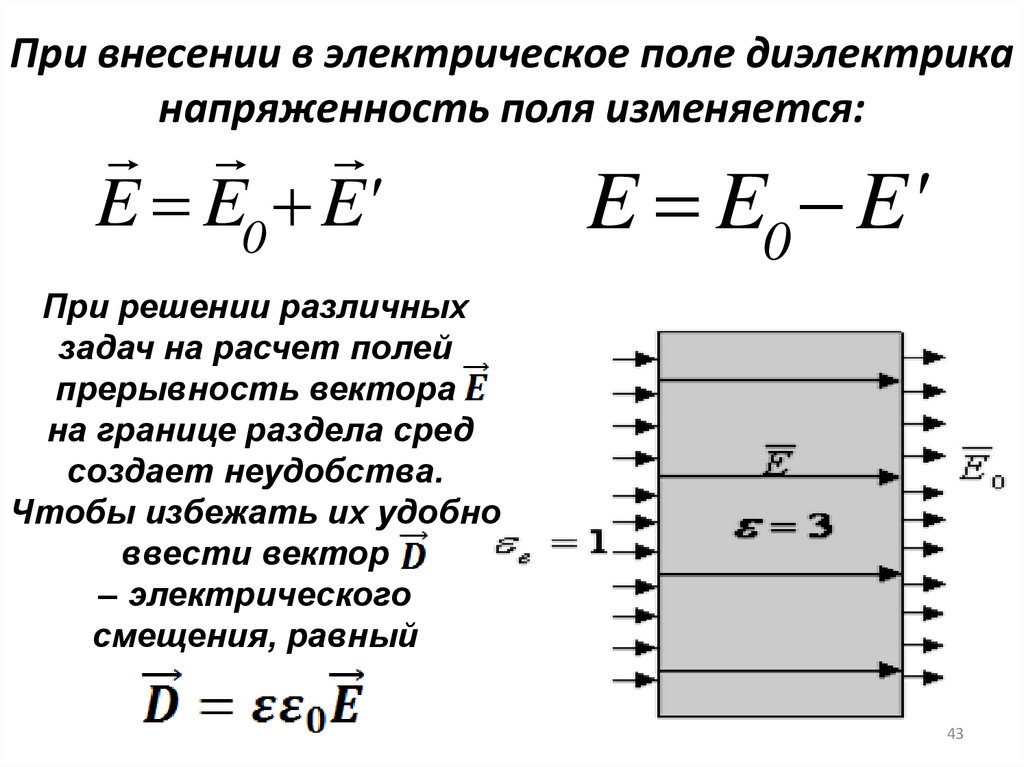
При внесении в электрическое поле диэлектрика
напряженность поля изменяется:
E E0 E'
E E0 E'
При решении различных
задач на расчет полей
прерывность вектора
на границе раздела сред
создает неудобства.
Чтобы избежать их удобно
ввести вектор
– электрического
смещения, равный
43

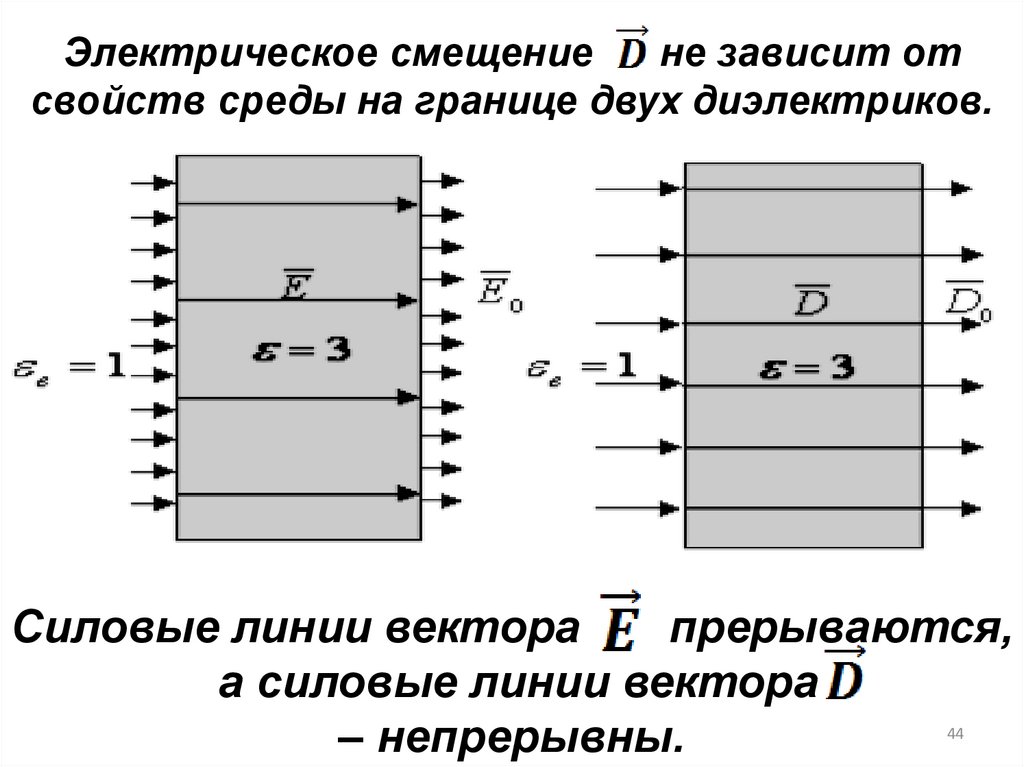
44.

Электрическое смещение
не зависит от
свойств среды на границе двух диэлектриков.
Силовые линии вектора
прерываются,
а силовые линии вектора
– непрерывны.
44

45. Теорема Остроградского – Гаусса для электрического смещения

Поток вектора электрического смещения через
произвольную замкнутую поверхность равен
алгебраической сумме зарядов, охваченных
этой поверхностью.
ФD D dS q
n
i
S
45

46.

Работа сил электрического поля
по перемещению заряда
На всякий заряд,
находящийся в
электрическом
поле, действует
сила, и поэтому
при движении
заряда в поле
совершается
определенная
работа.
46

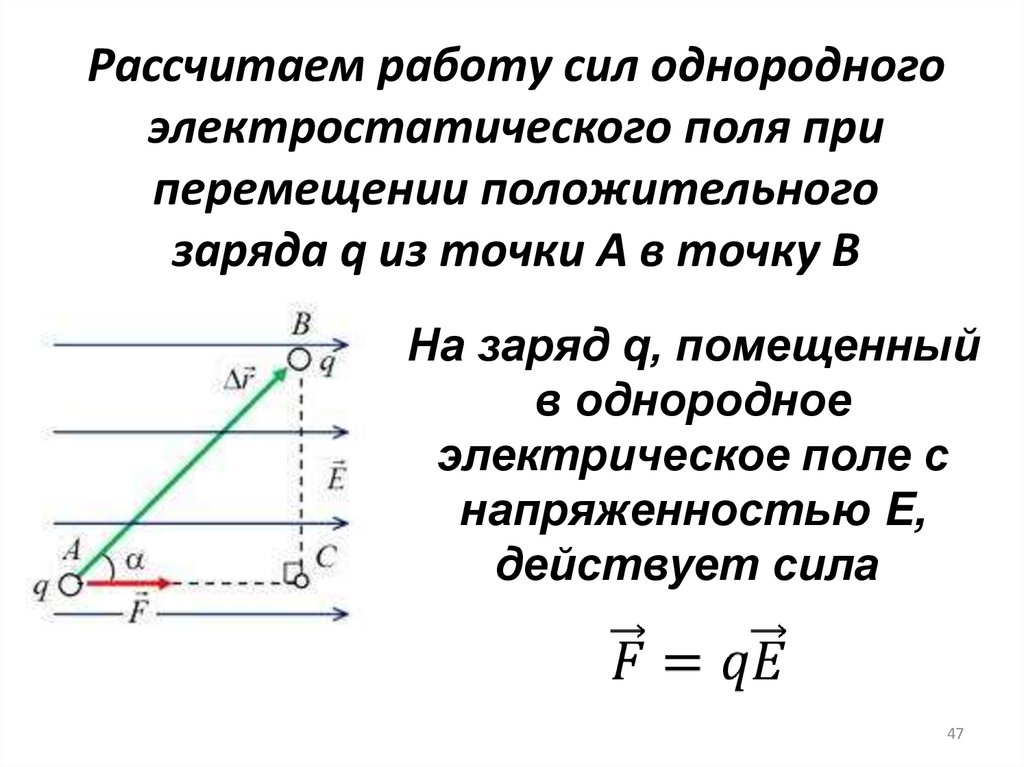
47.

Рассчитаем работу сил однородного
электростатического поля при
перемещении положительного
заряда q из точки A в точку B
На заряд q, помещенный
в однородное
электрическое поле с
напряженностью E,
действует сила
47

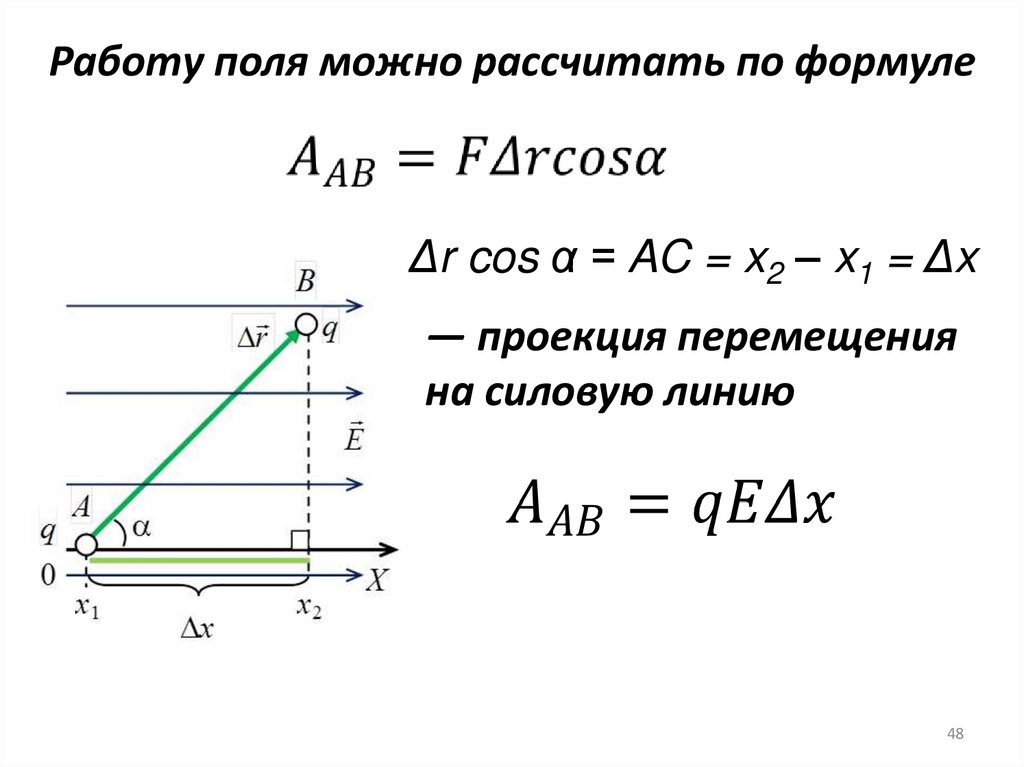
48.

Работу поля можно рассчитать по формуле
Δr cos α = AC = x2 – x1 = Δx
— проекция перемещения
на силовую линию
48

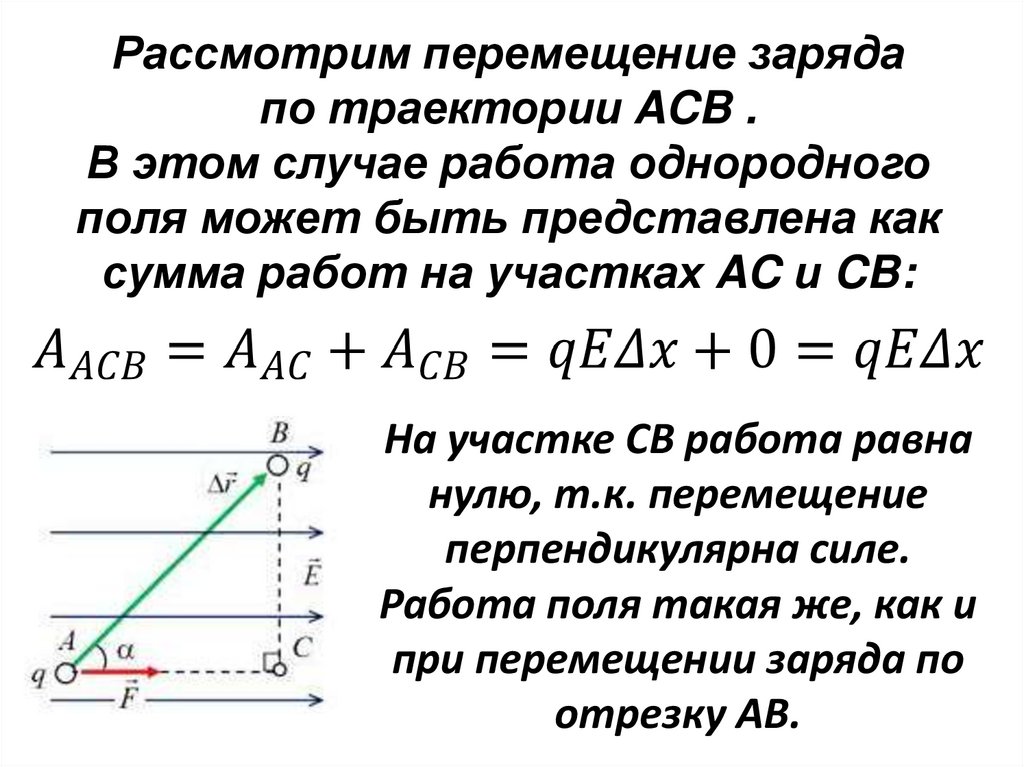
49.

Рассмотрим перемещение заряда
по траектории ACB .
В этом случае работа однородного
поля может быть представлена как
сумма работ на участках AC и CB:
На участке CB работа равна
нулю, т.к. перемещение
перпендикулярна силе.
Работа поля такая же, как и
при перемещении заряда по
отрезку AB.

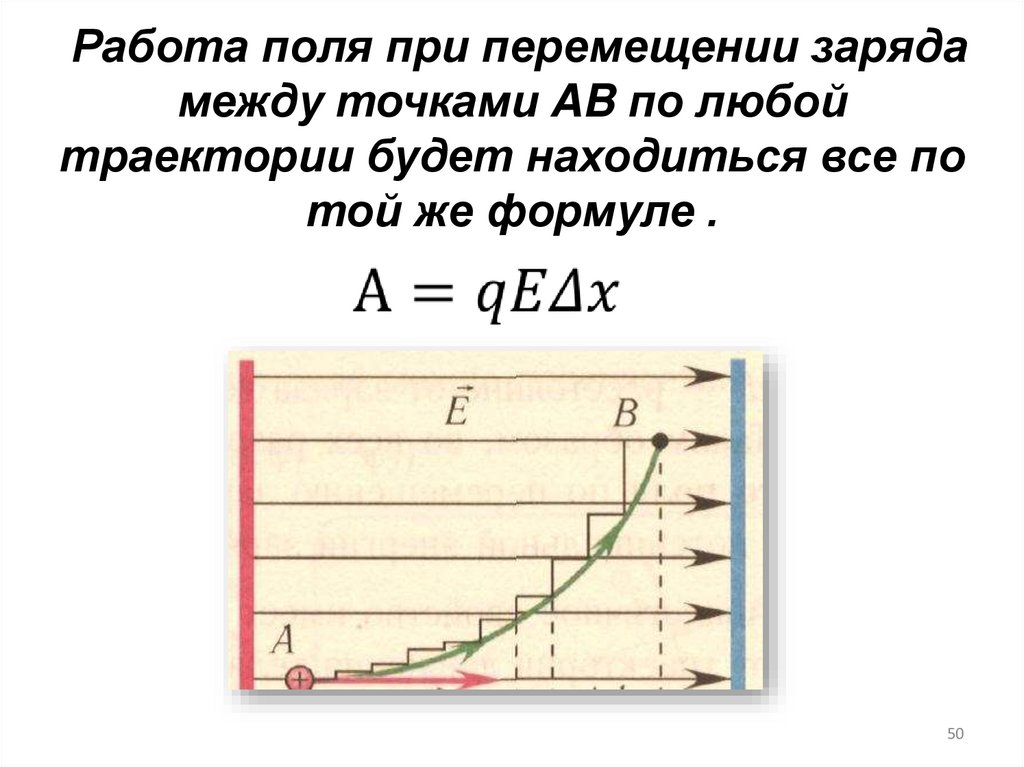
50.

Работа поля при перемещении заряда
между точками AB по любой
траектории будет находиться все по
той же формуле .
50

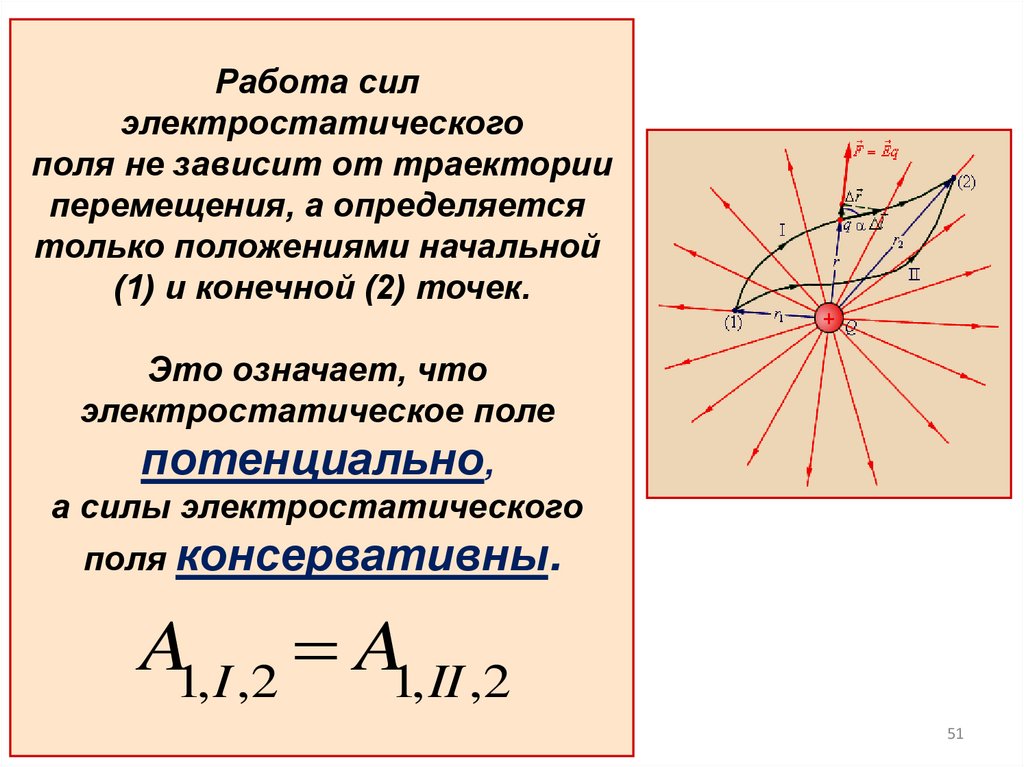
51.

Работа сил
электростатического
поля не зависит от траектории
перемещения, а определяется
только положениями начальной
(1) и конечной (2) точек.
Это означает, что
электростатическое поле
потенциально,
а силы электростатического
поля консервативны.
A1, I ,2 A1, II ,2
51

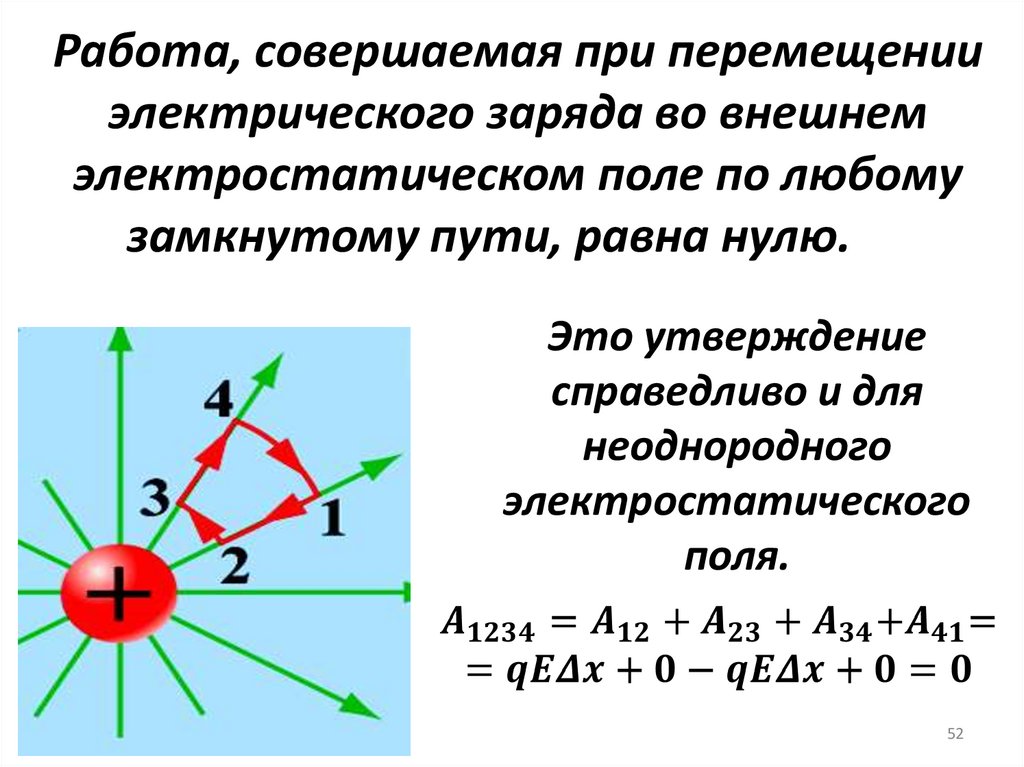
52.

Работа, совершаемая при перемещении
электрического заряда во внешнем
электростатическом поле по любому
замкнутому пути, равна нулю.
Это утверждение
справедливо и для
неоднородного
электростатического
поля.
52

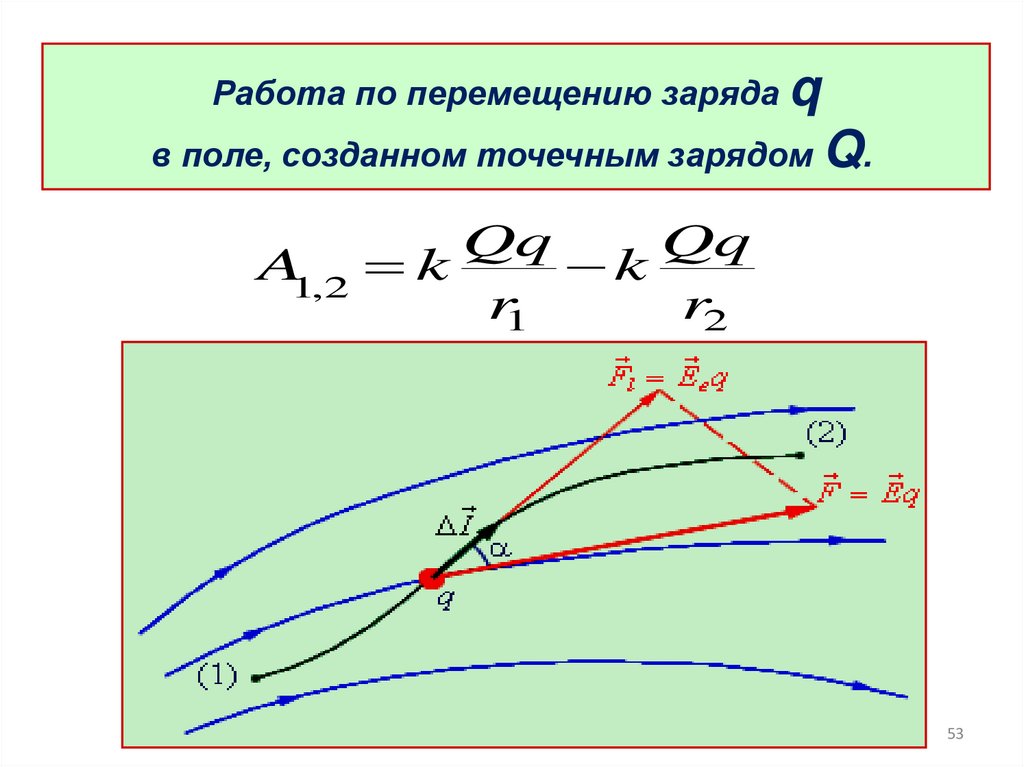
53.

Работа по перемещению заряда q
в поле, созданном точечным зарядом Q.
Qq
Qq
A1,2 k
k
r1
r2
53

54.

Работа консервативных сил совершается за счет
убыли потенциальной энергии, следовательно,
А1,2 можно представить, как разность
потенциальных энергий заряда q
в начальной и конечной точках траектории.
Qq
Qq
A1,2 k
k
W1 W2
r1
r2
Qq
W k
r
54

55. Потенциал равен потенциальной энергией единичного положительного заряда, находящегося в данной точке поля.

Знак потенциала определяется знаком заряда.
55

56. Потенциал электрического поля

- Энергетическая характеристика электрического
поля.
- Скалярная величина, равная отношению
потенциальной энергии заряда в заданной точке
поля к величине этого заряда.
- Потенциал электрического поля измеряется в
вольтах.
W
q
W
q
Дж
В Кл
56

57. Принцип суперпозиции полей

Если поле создано несколькими зарядами,
потенциал в любой точке равен
алгебраической сумме потенциалов,
созданных в этой точке каждым зарядом
в отдельности
(с учетом знаков потенциалов).
i
57

58. Связь между напряженностью и потенциалом

A F x qE x
Работа по перемещения положительного заряда q из одной
точки в другую может быть вычислена как через напряженность
поля, так и через потенциал.
A q 1 2 q
E
x
E grad
d
E
dx
Знак минус показывает, что вектор напряженности
направлен в сторону убывания потенциала.
58

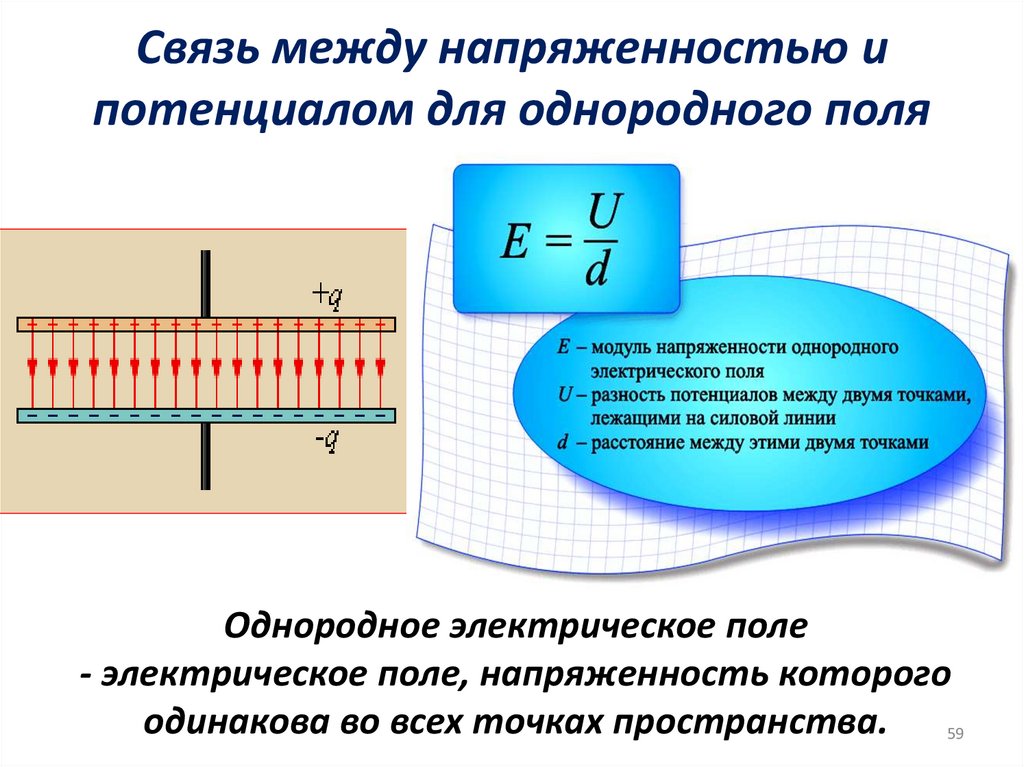
59. Связь между напряженностью и потенциалом для однородного поля

Однородное электрическое поле
- электрическое поле, напряженность которого
одинакова во всех точках пространства. 59

60. Разность потенциалов

Разность потенциалов двух точек
электростатического поля – это физическая
скалярная величина, определяемая работой,
совершаемой кулоновскими силами при
перемещении единичного положительного заряда
из одной точки в другую.
60

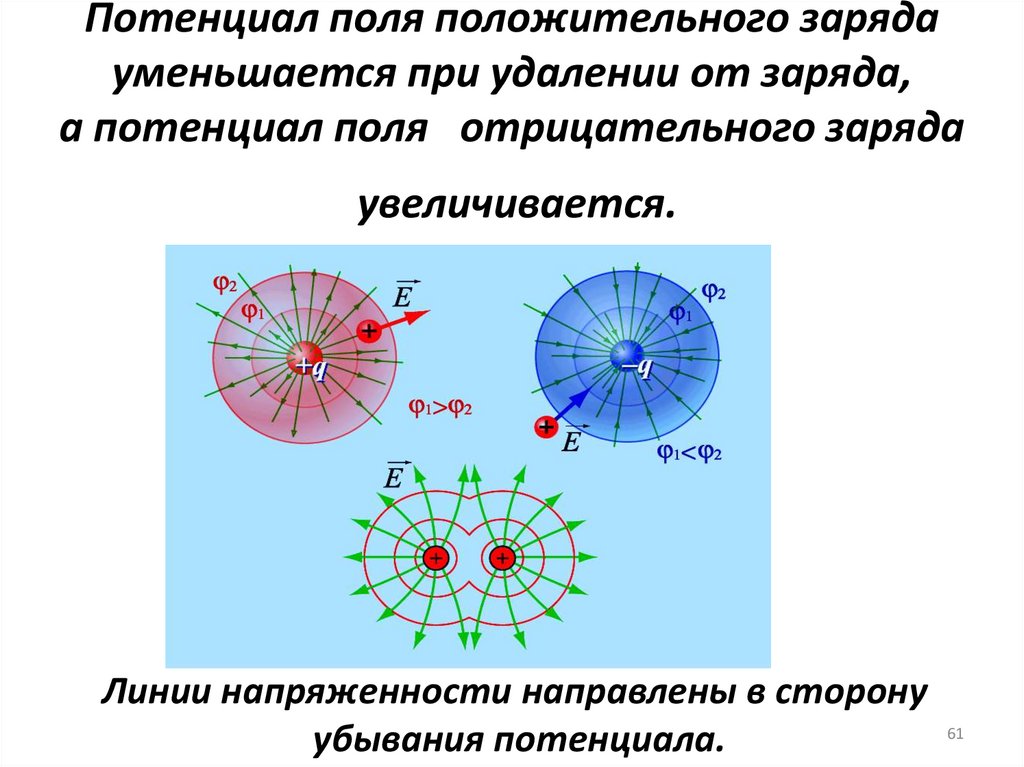
61. Потенциал поля положительного заряда уменьшается при удалении от заряда, а потенциал поля отрицательного заряда увеличивается.

Линии напряженности направлены в сторону
61
убывания потенциала.

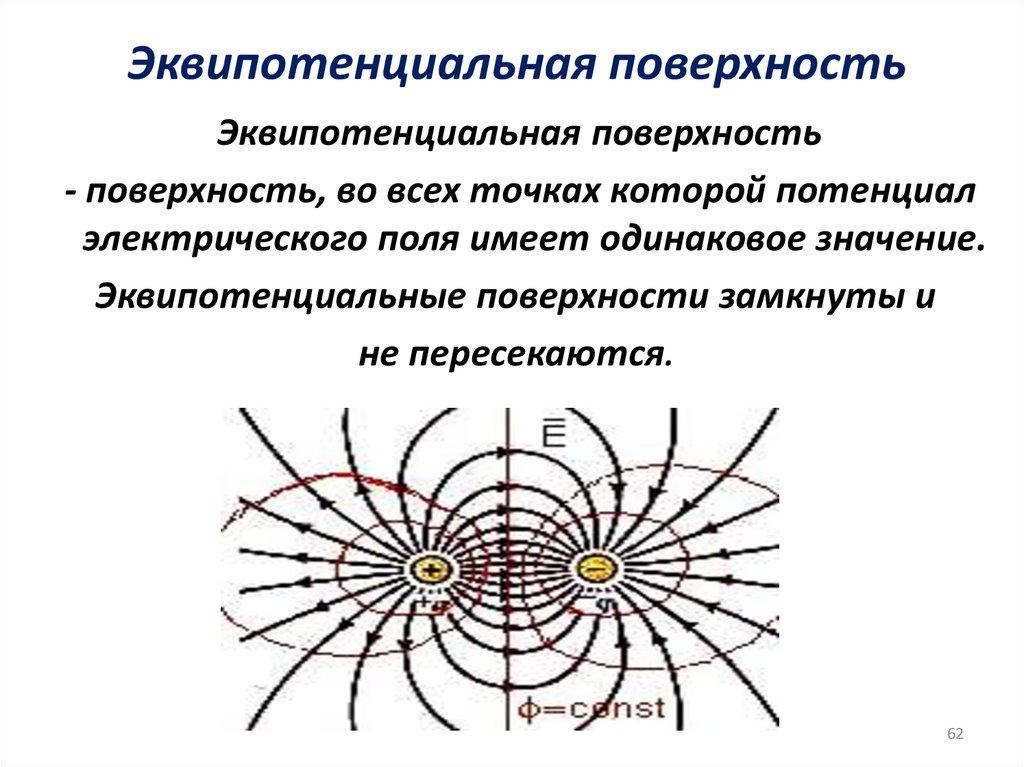
62. Эквипотенциальная поверхность

Эквипотенциальная поверхность
- поверхность, во всех точках которой потенциал
электрического поля имеет одинаковое значение.
Эквипотенциальные поверхности замкнуты и
не пересекаются.
62

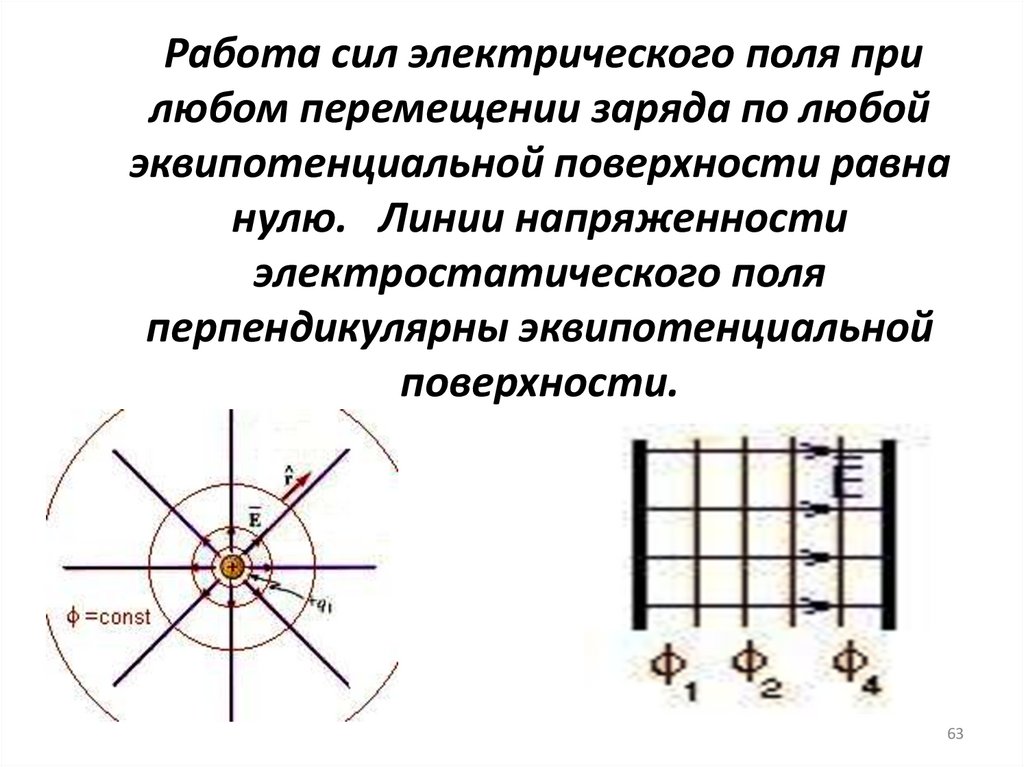
63.

Работа сил электрического поля при
любом перемещении заряда по любой
эквипотенциальной поверхности равна
нулю. Линии напряженности
электростатического поля
перпендикулярны эквипотенциальной
поверхности.
63

64.

Энергия электрического поля
64

65.

65

66.

66

67.

67

68.

68

69.

69

70.

70

71.

71

72.

72

73.

73

74.

74

75.

75

76.

76

77.

77

78.

78

79.

79

80.

80

81.

81

82.

82

83.

83

84.

84

85.

85

86.

86

87. Электрический разряд

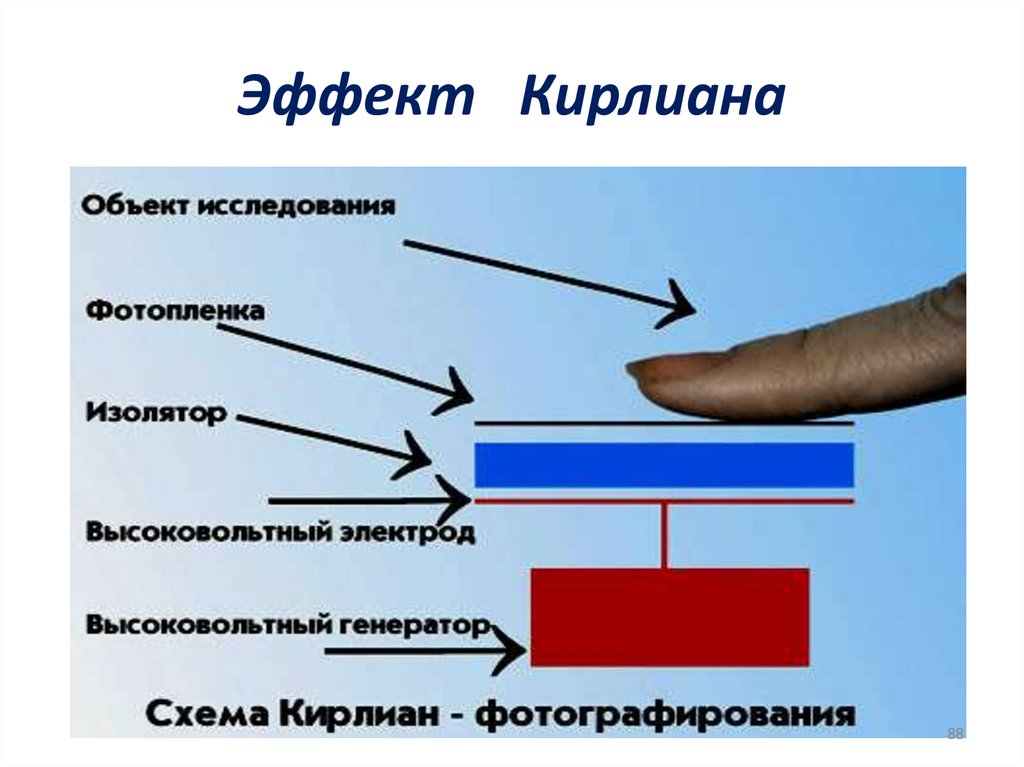
87

88. Эффект Кирлиана

88

89.

89

90.

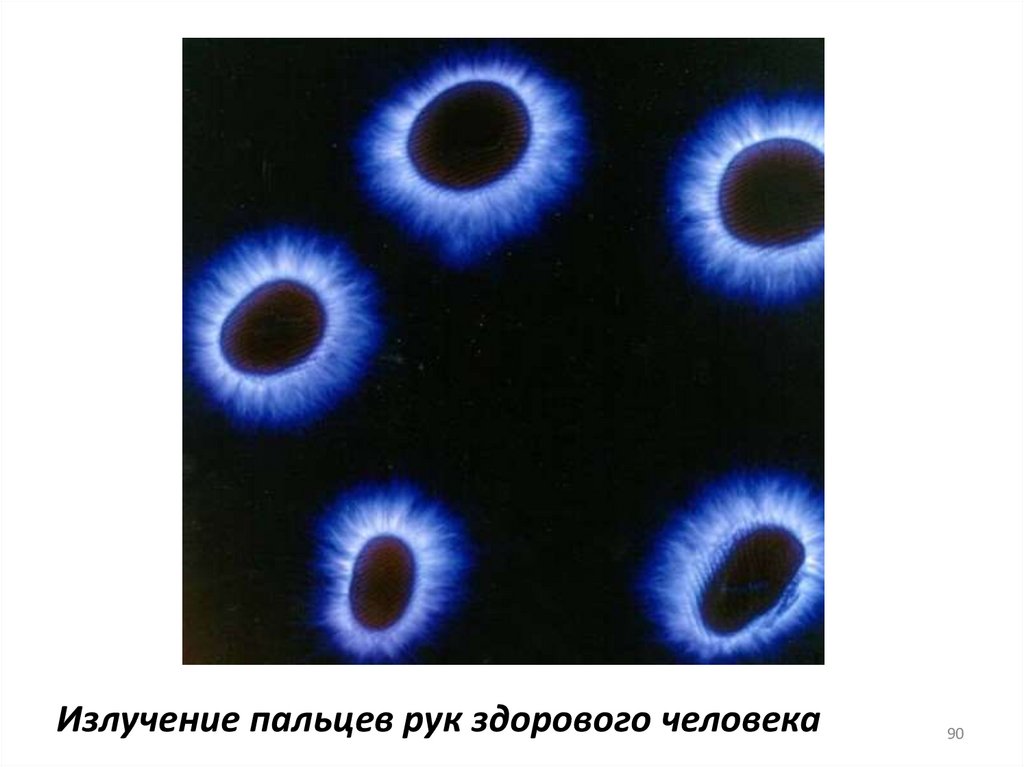
Излучение пальцев рук здорового человека
90

91.

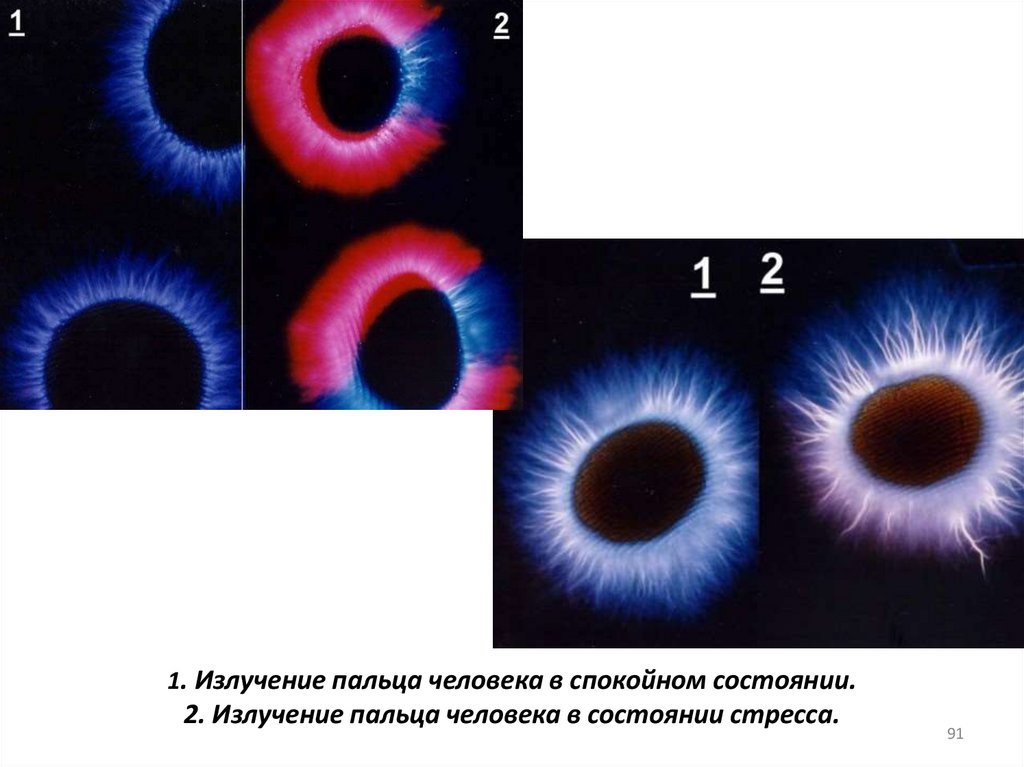
1. Излучение пальца человека в спокойном состоянии.
2. Излучение пальца человека в состоянии стресса.
91

92.

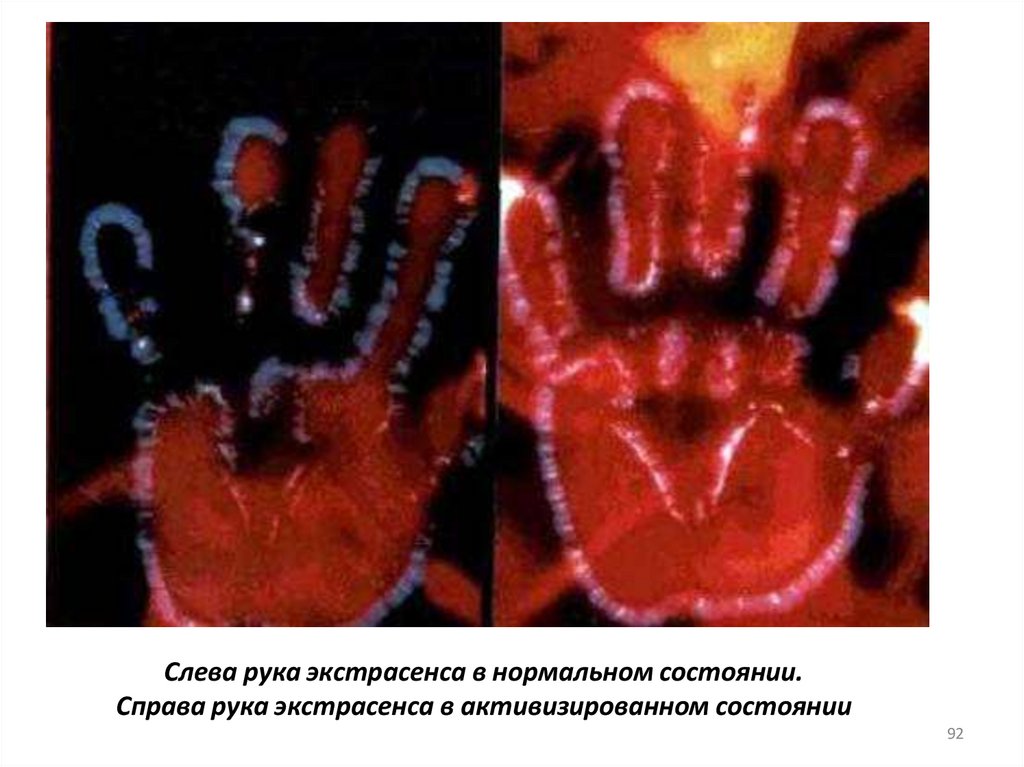
Слева рука экстрасенса в нормальном состоянии.
Справа рука экстрасенса в активизированном состоянии
92

93.

93

94.

94

95.

1. Излучение копейки, подобранной на улице.
2. Излучение копейки после энергоочистки.
95

96.

96