Similar presentations:
Электростатика. Лекция № 6
1.
ЭлектростатикаЛекция № 6
2.
План лекции:1.
2.
3.
4.
5.
6.
7.
Электрический заряд. Взаимодействие заряженных тел.
Закон Кулона. Закон сохранения заряда.
Электрическое поле. Напряженность электрического поля.
Электрическое поле точечного заряда. Принцип
суперпозиции полей.
Работа сил поля при перемещении заряда. Циркуляция
вектора напряженности электростатического поля.
Потенциал и разность потенциалов. Потенциал поля
точечного заряда. Связь между напряженностью
электрического поля и разностью потенциалов.
Эквипотенциальные поверхности.
Теорема Остроградского-Гаусса.
Проводники и диэлектрики в электрическом поле.
Электроемкость. Энергия электрического поля.
3.
1. Электрический заряд. Взаимодействиезаряженных тел. Закон Кулона. Закон
сохранения заряда
• Электростатика изучает взаимодействие и
условия равновесия покоящихся
электрически заряженных тел, а также
свойства этих тел, обусловленные
электрическими зарядами.
4.
1. Электрический заряд. Взаимодействиезаряженных тел. Закон Кулона. Закон
сохранения заряда
• Гильберт назвал тела, способные
после натирания притягивать
легкие предметы,
наэлектризованными.
Уильям
Гильберт
(24.05.1544 –
30.10.1603)
5.
1. Электрический заряд. Взаимодействиезаряженных тел. Закон Кулона. Закон
сохранения заряда
• Электрический заряд – это физическая
величина, характеризующая свойство тел
или частиц вступать в электромагнитное
взаимодействие.
• Существует два вида зарядов, которые
условно называют положительными и
отрицательными.
• Единица измерения заряда в СИ кулон
(Кл).
1Кл 1 А с
6.
1. Электрический заряд. Взаимодействиезаряженных тел. Закон Кулона. Закон
сохранения заряда
• Электрический заряд дискретен,
т. е. заряд любого тела составляет
целое кратное от элементарного
электрического заряда:
Роберт
Эндрюс
Милликен
(1868 – 1953)
q Ne
e 1,6 10
19
Кл
7.
1. Электрический заряд. Взаимодействиезаряженных тел. Закон Кулона. Закон
сохранения заряда
Шарль Кулон
(1736 – 1806)
Крутильные
весы
• Точечным зарядом называют
заряженное тело, размерами которого
можно пренебречь.
• Закон Кулона: сила электрического
взаимодействия между двумя
точечными электрическими зарядами
прямо пропорциональна
произведению величин зарядов и
обратно пропорциональна квадрату
расстояния между ними и направлена
вдоль прямой, соединяющей эти
заряды:
q1 q 2
F k
r2
8.
1. Электрический заряд. Взаимодействиезаряженных тел. Закон Кулона. Закон
сохранения заряда
•k
1
4 0
для вакуума, k
1
4 0
для среды;
• относительная диэлектрическая
проницаемость среды;
• электрическая постоянная:
0 8,85 10 12 Кл2 / Н м2
9.
1. Электрический заряд. Взаимодействиезаряженных тел. Закон Кулона. Закон
сохранения заряда
• Сила F направлена по прямой, соединяющей
взаимодействующие заряды, т. е. является
центральной, и соответствует притяжению ( F 0 )
в случае разноименных зарядов и отталкиванию
( F 0 ) в случае одноименных зарядов. Эта сила
называется кулоновской силой.
10.
1. Электрический заряд. Взаимодействиезаряженных тел. Закон Кулона. Закон
сохранения заряда
• Закон сохранения
электрического заряда:
алгебраическая сумма
электрических зарядов
замкнутой системы тел остается
Майкл Фарадей
постоянной при любых
(1791 – 1867)
процессах в этой системе:
q1 q 2 q 3 q n const
11.
1. Электрический заряд. Взаимодействиезаряженных тел. Закон Кулона. Закон
сохранения заряда
По характеру и значению
электропроводности
проводники
диэлектрики
полупроводники
12.
2. Электрическое поле. Напряженностьэлектрического поля. Электрическое поле
точечного заряда. Принцип суперпозиции полей
• Электрическое поле вид материи,
посредством которой осуществляется
взаимодействие электрических зарядов.
• Если электрические заряды неподвижны, то
поле является электростатическим.
• Пробный точечный положительный заряд
такой заряд, который не искажает
исследуемое поле (не вызывает
перераспределения зарядов, создающих
поле).
13.
2. Электрическое поле. Напряженностьэлектрического поля. Электрическое поле
точечного заряда. Принцип суперпозиции полей
• Напряженность поля физическая
величина, равная отношению силы, с
которой поле действует на точечный
положительный (пробный) заряд q,
помещенный в данную точку поля, к
величине этого заряда:
F
E
q
14.
2. Электрическое поле. Напряженностьэлектрического поля. Электрическое поле
точечного заряда. Принцип суперпозиции полей
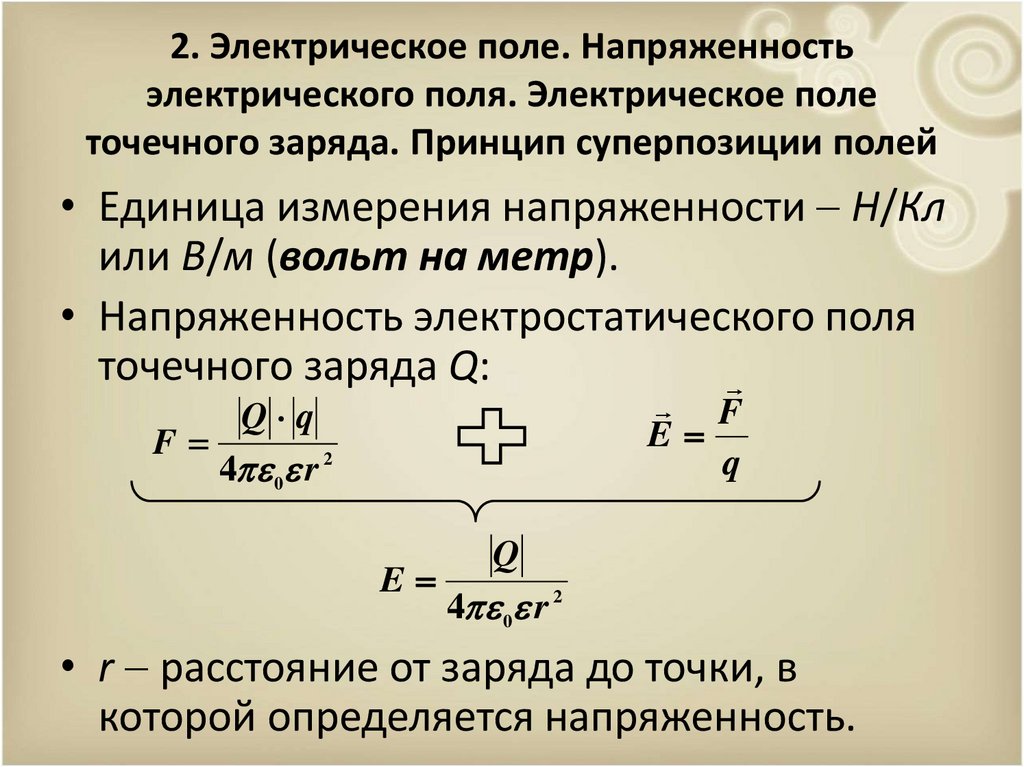
• Единица измерения напряженности Н/Кл
или В/м (вольт на метр).
• Напряженность электростатического поля
точечного заряда Q:
F
E
q
Q q
F
4 0 r 2
E
Q
4 0 r 2
• r расстояние от заряда до точки, в
которой определяется напряженность.
15.
2. Электрическое поле. Напряженностьэлектрического поля. Электрическое поле
точечного заряда. Принцип суперпозиции полей
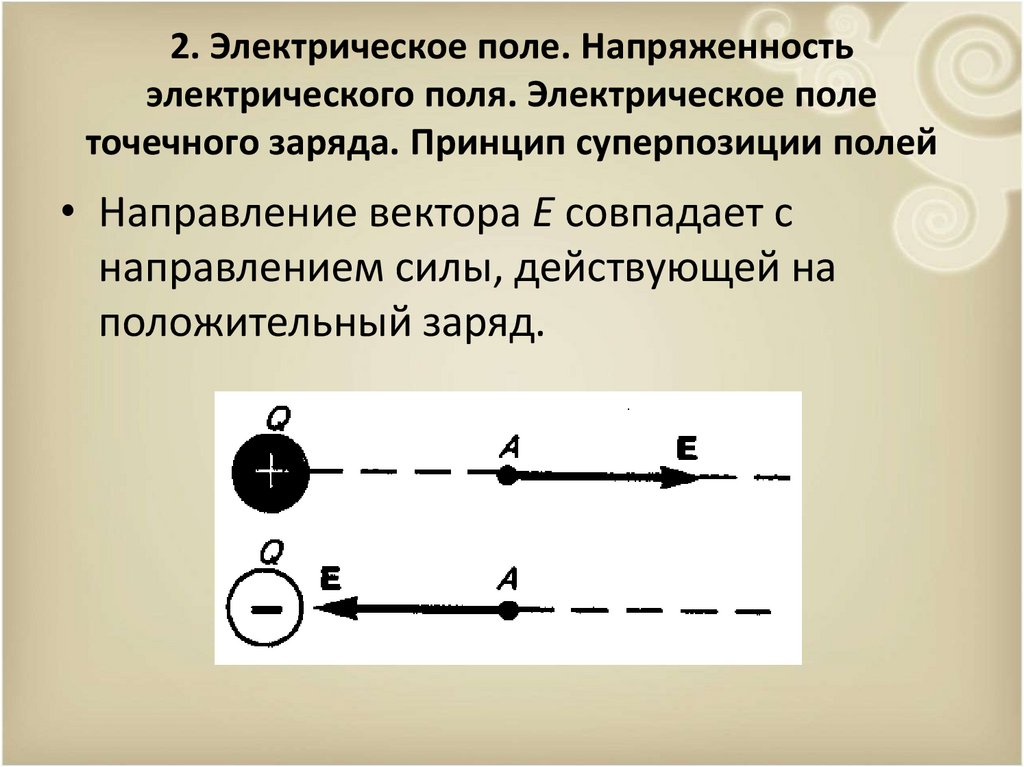
• Направление вектора Е совпадает с
направлением силы, действующей на
положительный заряд.
16.
2. Электрическое поле. Напряженностьэлектрического поля. Электрическое поле
точечного заряда. Принцип суперпозиции полей
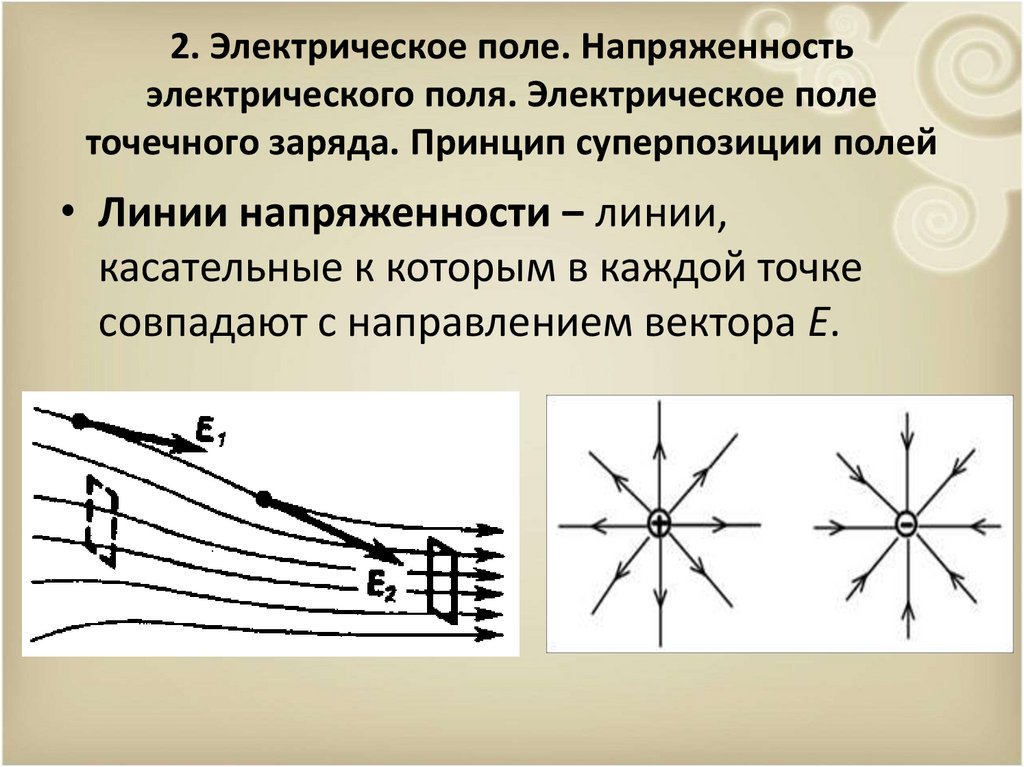
• Линии напряженности ‒ линии,
касательные к которым в каждой точке
совпадают с направлением вектора Е.
17.
2. Электрическое поле. Напряженностьэлектрического поля. Электрическое поле
точечного заряда. Принцип суперпозиции полей
• Принцип суперпозиции: напряженность
поля, созданного двумя и более зарядами,
находится как векторная сумма полей,
созданных каждым зарядом в
отдельности:
E E1 E 2 E n
18.
2. Электрическое поле. Напряженностьэлектрического поля. Электрическое поле
точечного заряда. Принцип суперпозиции полей
• В теории дальнодействия принимается, что
электрические явления определяются
мгновенным взаимодействием зарядов на
любых расстояниях.
• В теории близкодействия, все электрические
явления определяются изменениями полей
зарядов, причем эти изменения
распространяются в пространстве от точки к
точке с конечной скоростью.
19.
3. Работа сил поля при перемещениизаряда. Циркуляция вектора напряженности
электростатического поля
• При перемещении точечного заряда q на
расстояние dl в электрическом поле с
напряженностью E совершается работа:
dA Fdl cos qEdl cos qEdr qE l dl
F
dr
dl
q
1
r2
r1
Q
где угол между векторами E и dl ,
2 • dr dl cos проекция перемещения на
направление силовой линии,
• E E cos проекция вектора
напряженности на направление
перемещения.
l
20.
3. Работа сил поля при перемещениизаряда. Циркуляция вектора напряженности
электростатического поля
• Работа по перемещению заряда в
электростатическом поле не зависит
от формы траектории.
dr
qQ 1 1
A12 qEdr
2
1
4 0 1 r
4 0 r1 r2
2
2
• Электростатическое поле точечного заряда
является потенциальным, а
электростатические силы ‒
консервативными.
21.
3. Работа сил поля при перемещениизаряда. Циркуляция вектора напряженности
электростатического поля
2
A12 q E l dl
1
• Циркуляция вектора E
E l dl 0
• Циркуляция вектора напряженности
электростатического поля равна нулю.
• Силовые поля с такими свойствами
называются потенциальными.
• Электростатическое поле потенциально.
22.
4. Потенциал и разность потенциалов. Потенциал поляточечного заряда. Связь между напряженностью
электрического поля и разностью потенциалов.
Эквипотенциальные поверхности
• Работа в потенциальном поле равна
изменению потенциальной энергии
системы «поле-заряд», взятым с
противоположным знаком:
A (W 2 W1 )
• где W1, W2 значения потенциальной
энергии в начальной и конечной точках.
A q( 1 2 )
23.
4. Потенциал и разность потенциалов. Потенциал поляточечного заряда. Связь между напряженностью
электрического поля и разностью потенциалов.
Эквипотенциальные поверхности
• Разность потенциалов между двумя точками,
которая численно равна разности
потенциальных энергий заряда в этих точках,
отнесенной к величине заряда:
W1 W2
( 1 2 )
q
q
• Разность потенциалов между двумя
точками можно определить и как работу по
перемещению единичного положительного
заряда из первой точки во вторую.
24.
4. Потенциал и разность потенциалов. Потенциал поляточечного заряда. Связь между напряженностью
электрического поля и разностью потенциалов.
Эквипотенциальные поверхности
• Потенциал данной точки поля численно
равен работе по перемещению единичного
положительного заряда из данной точки на
бесконечность:
A
q
• Потенциал поля точечного заряда Q на
расстоянии r от заряда равен:
Q
4 0 r
25.
4. Потенциал и разность потенциалов. Потенциал поляточечного заряда. Связь между напряженностью
электрического поля и разностью потенциалов.
Эквипотенциальные поверхности
• Потенциал и разность потенциалов
измеряются в вольтах.
1В 1 Дж / Кл
dA qEdr qd
• где d изменение потенциала при
перемещении вдоль силовой линии на
расстояние dr.
• Знак ( ) означает, что при увеличении
расстояния потенциал уменьшается.
26.
4. Потенциал и разность потенциалов. Потенциал поляточечного заряда. Связь между напряженностью
электрического поля и разностью потенциалов.
Эквипотенциальные поверхности
• Связь между напряженностью
электрического поля и изменением
потенциала:
d
E
dr
1В / м 1Н / Кл
• Эквипотенциальной поверхностью
называют геометрическое место точек
одинакового потенциала.
27.
5. Теорема Остроградского-Гаусса• Величина
dФE En dS EdS
Карл Фридрих
Гаусс
(1777 – 1855)
• называется потоком вектора
напряженности через площадку
dS.
28.
5. Теорема Остроградского-Гаусса• Для произвольной замкнутой поверхности S
поток вектора Е сквозь эту поверхность:
ФE En dS EdS
S
S
• Для замкнутых поверхностей за
положительное направление нормали
принимается внешняя нормаль, т. е.
нормаль, направленная наружу области,
охватываемой поверхностью.
29.
5. Теорема Остроградского-Гаусса• Теорема Остроградского-Гаусса: поток
вектора напряженности через
произвольную замкнутую поверхность
равен алгебраической сумме зарядов,
охватываемых этой поверхностью,
деленной на 0:
1 N
Фе E n dS
qi
0 i 1
30.
5. Теорема Остроградского-Гаусса• Для одного точечного заряда, если
охватывающая его поверхность является
сферой, в центре которой находится этот
заряд.
En E
• Площадь сферы:
2
S 4 r
q
1
2
Фе E dS
4 r
q
2
S
4 0 r
0
31.
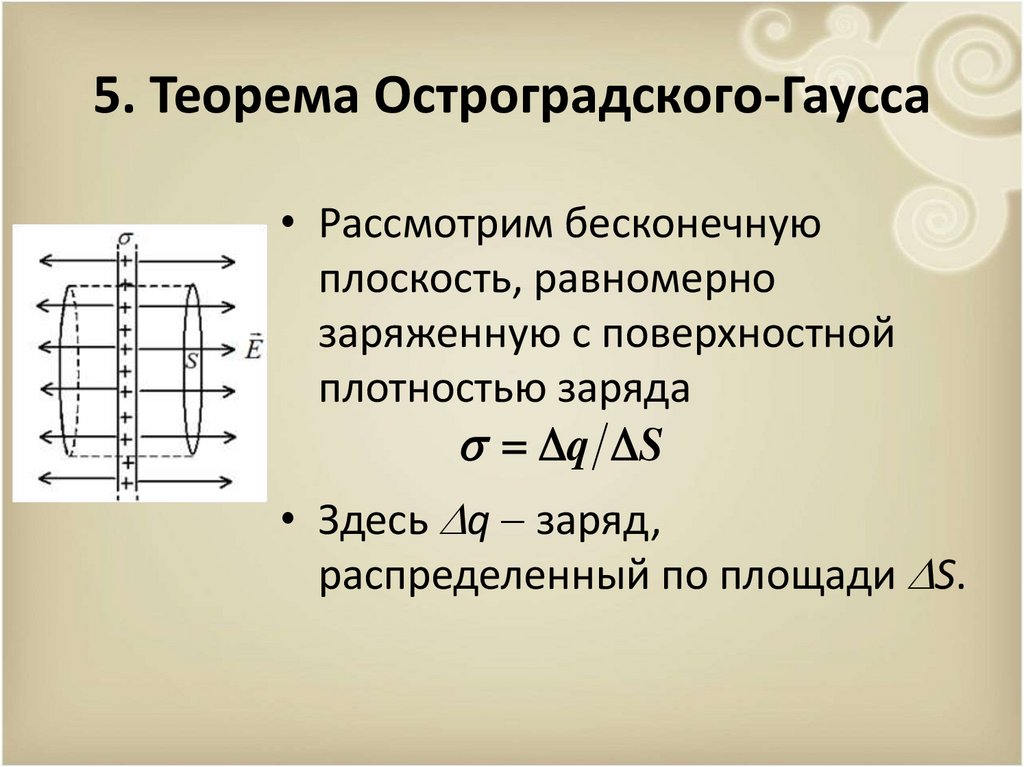
5. Теорема Остроградского-Гаусса• Рассмотрим бесконечную
плоскость, равномерно
заряженную с поверхностной
плотностью заряда
q S
• Здесь q заряд,
распределенный по площади S.
32.
5. Теорема Остроградского-Гаусса• Полный поток равен потоку через два
основания:
Фе 2 ES
• Суммарный заряд внутри цилиндра равен:
q σS
• Выражение для напряженности поля
бесконечной заряженной плоскости:
E
2 0
33.
5. Теорема Остроградского-Гаусса• Используя связь между напряженностью и
потенциалом, найдем выражение для
разности потенциалов двух точек в поле
заряженной плоскости.
d
E
dr
d Edr
• Подставив сюда выражение для
напряженности поля и проинтегрировав,
получим:
r1 r2
2 1
2 0
34.
5. Теорема Остроградского-Гаусса• Здесь r1 и r2 кратчайшие расстояния точек
до заряженной поверхности (вдоль силовой
линии).
• Для поля заряженного шара (для точек,
находящихся на расстоянии r от центра
большем, чем радиус шара R):
1
q
E
4 0 r 2
1
q
4 0 r
35.
6. Проводники и диэлектрики вэлектрическом поле
• Явление электростатической индукции под
действием поля часть электронов
концентрируется в тонком слое вблизи одной из
поверхностей.
• Если в присутствии поля проводник разделить на
две части, то каждая из них окажется заряженной.
Заряд сохранится и при исчезновении внешнего
поля.
36.
6. Проводники и диэлектрики вэлектрическом поле
• В диэлектриках нет заряженных частиц,
способных свободно перемещаться по
объему.
• Под действием поля происходит поляризация
молекул диэлектрика образование диполей,
оси которых ориентированы вдоль внешнего
поля.
• На границах диэлектрика, где у молекул есть
соседи только с одной стороны, образуются
нескомпенсированные заряды, называемые
поляризационными или связанными.
37.
6. Проводники и диэлектрики вэлектрическом поле
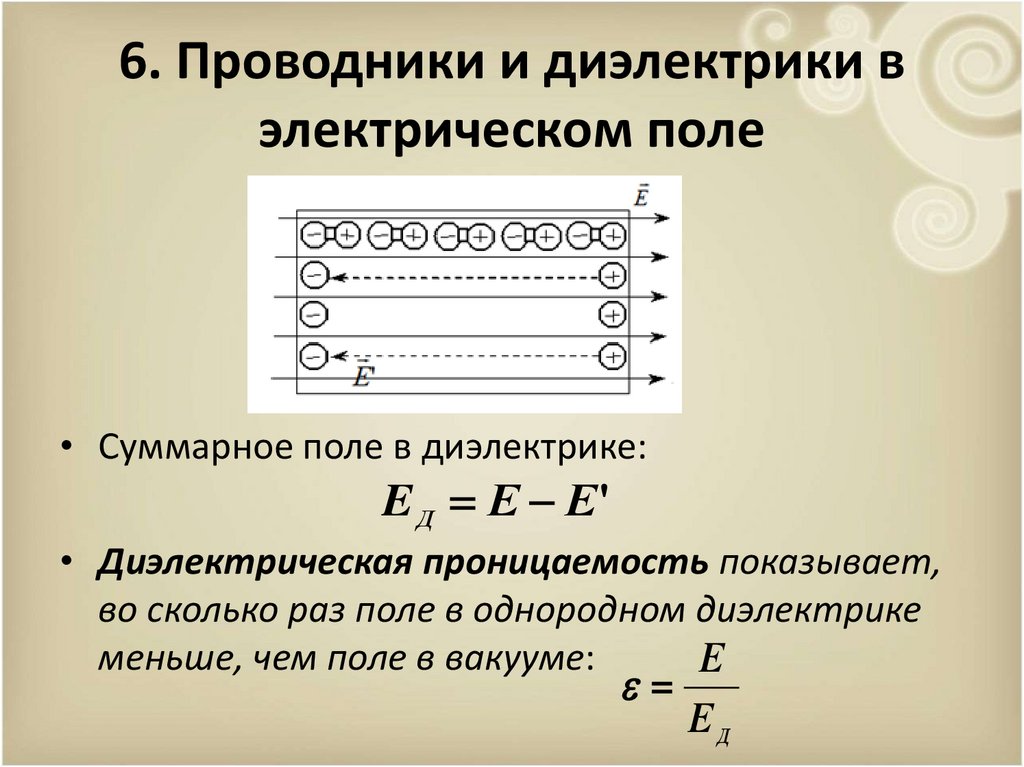
• Суммарное поле в диэлектрике:
E Д Е Е'
• Диэлектрическая проницаемость показывает,
во сколько раз поле в однородном диэлектрике
меньше, чем поле в вакууме:
Е
ЕД
38.
7. Электроемкость. Энергияэлектрического поля
• Электроемкость проводника величина,
численно равная величине заряда q,
вызвавшей повышение его потенциала на
единицу:
C
q
q C
• В СИ электроемкость измеряется в
фарадах:
1Ф 1Кл / В
1 мкФ 10 6 Ф, 1пФ 10 12 Ф
39.
7. Электроемкость. Энергияэлектрического поля
• Из выражения для потенциала поверхности
шара:
q
4 0 R
• находим электроемкость шара:
C 4 0 R
• Электроемкость земного шара:
7 10 Ф
4
40.
7. Электроемкость. Энергияэлектрического поля
• Конденсатор система, состоящая из двух
разделенных диэлектриком проводников
(обкладок), на которых могут
накапливаться заряды противоположных
знаков.
q
C
• где – разность
потенциалов
между
обкладками.
41.
7. Электроемкость. Энергияэлектрического поля
• Электроемкость плоского конденсатора может
быть найдена, если учесть что напряженность
поля внутри конденсатора создается двумя
заряженными пластинами:
E
0
• разность потенциалов:
2 1
d
0
• где d расстояние между пластинами; заряд на
пластинах: q σS , S площадь пластин.
42.
7. Электроемкость. Энергияэлектрического поля
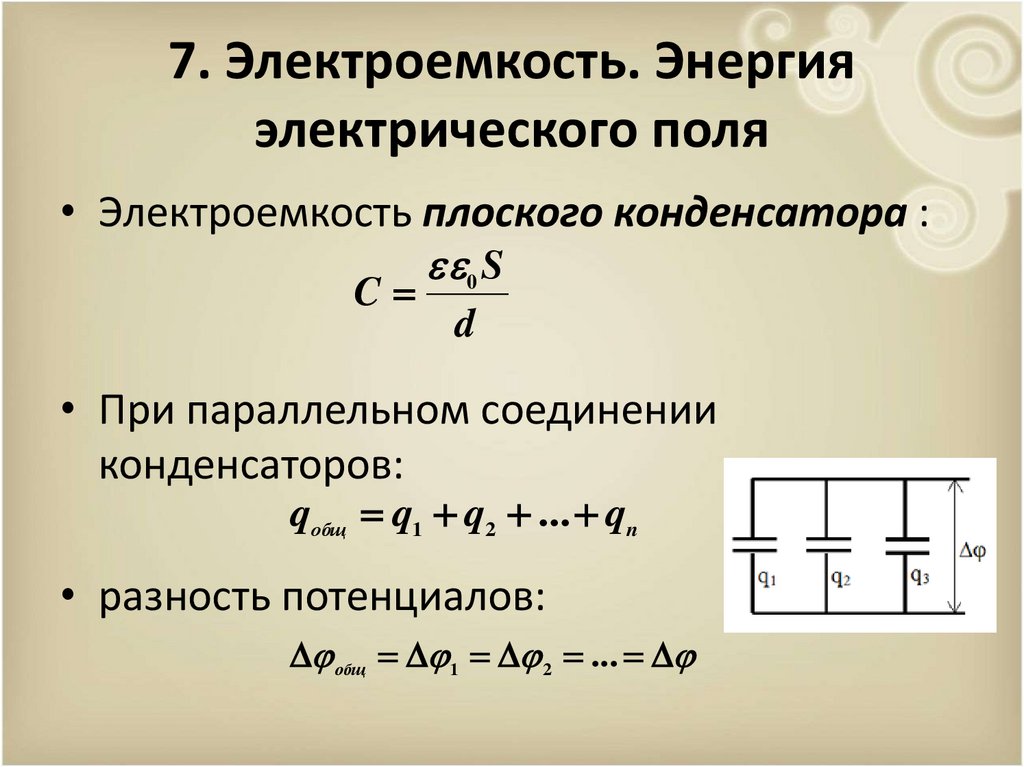
• Электроемкость плоского конденсатора :
C
0 S
d
• При параллельном соединении
конденсаторов:
qобщ q1 q2 ... qn
• разность потенциалов:
общ 1 2 ...
43.
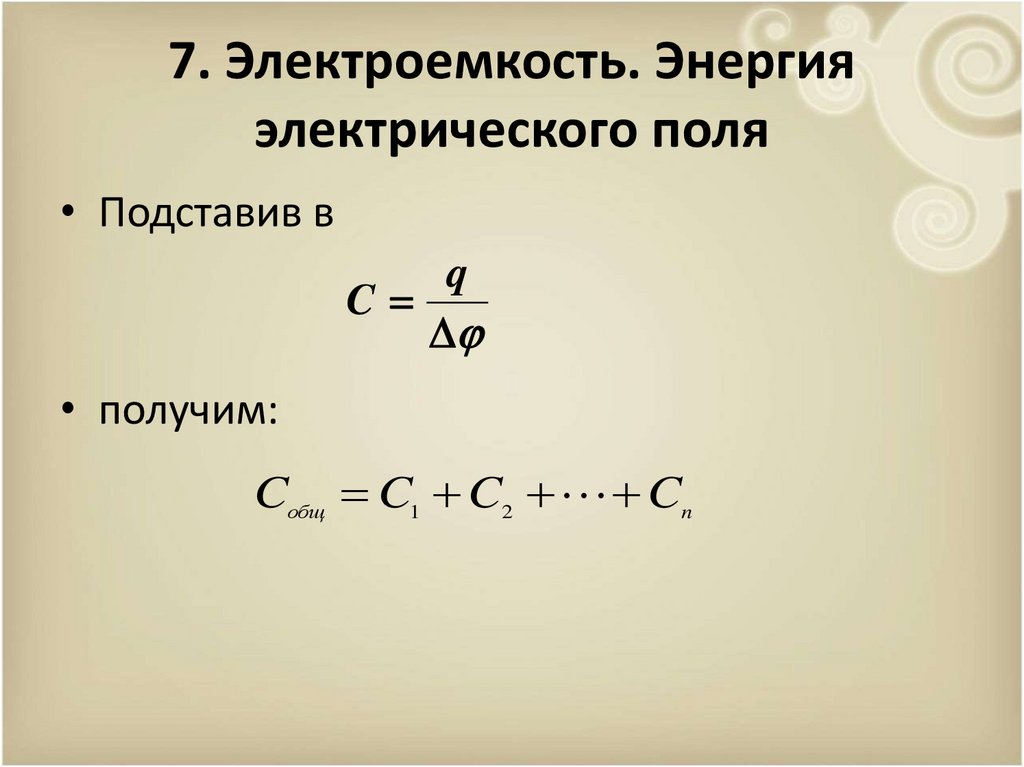
7. Электроемкость. Энергияэлектрического поля
• Подставив в
q
C
• получим:
Cобщ C1 C2 Cn
44.
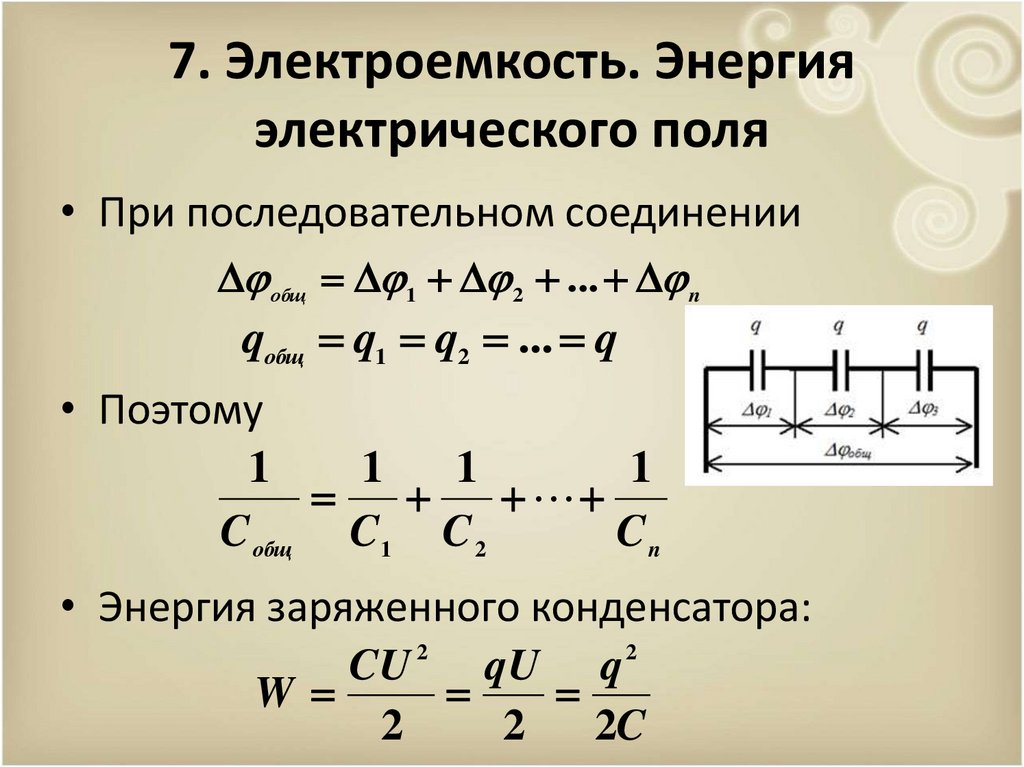
7. Электроемкость. Энергияэлектрического поля
• При последовательном соединении
общ 1 2 ... n
qобщ q1 q2 ... q
• Поэтому
1
1
1
1
C общ C1 C 2
Cn
• Энергия заряженного конденсатора:
2
2
CU
qU q
W
2
2
2C



































 physics
physics








