Электродинамика

1.

2.

2

3.

3

4.

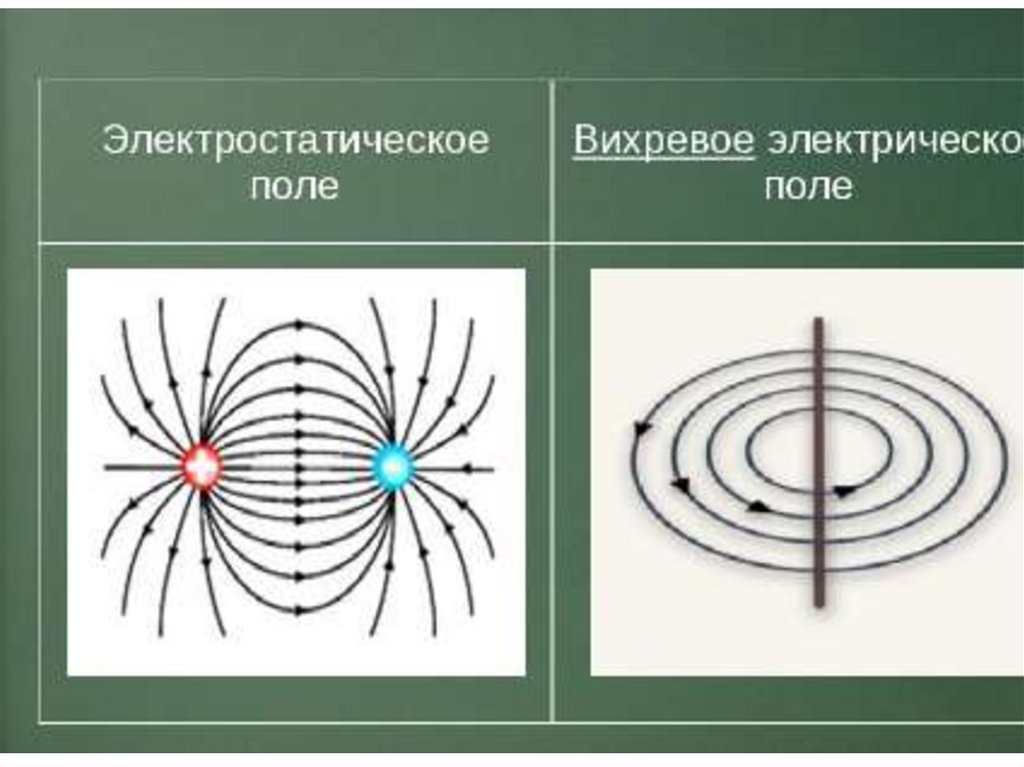
Электростатика
– раздел электродинамики,
изучающий взаимодействие
неподвижных зарядов.
4

5. Электрическое поле -

• особая форма существования материи,
посредством которой осуществляется
взаимодействие между покоящимися или
движущимися электрическими зарядами.
• Все тела в природе можно разделить на
проводники ( металлы), диэлектрики (спирт,
стекло, дист. вода), полупроводники ( индий,
германий).
5

6. Электрическое поле (2)

Электрическое поле –
силовое поле, посредством которого
взаимодействуют электрические заряды.
Электрическое поле,
созданное неподвижными зарядами,
называется электростатическим.

7.

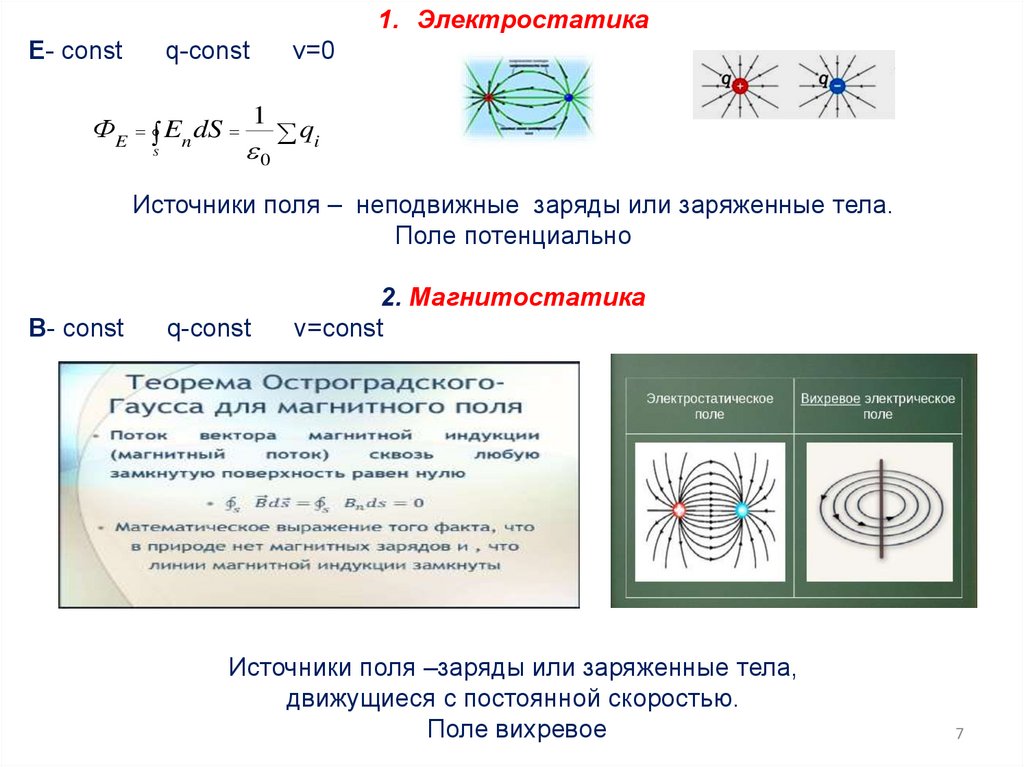
1. Электростатика
Е- const
q-const
ФE En dS
S
v=0
1
0
qi
Источники поля – неподвижные заряды или заряженные тела.
Поле потенциально
В- const
q-const
2. Магнитостатика
v=const
Источники поля –заряды или заряженные тела,
движущиеся с постоянной скоростью.
Поле вихревое
7

8.

Электрический заряд
- физическая величина, которая
характеризует свойство тел или частиц
вступать в электромагнитные
взаимодействия и определяет значения
сил и энергий при таких взаимодействиях.
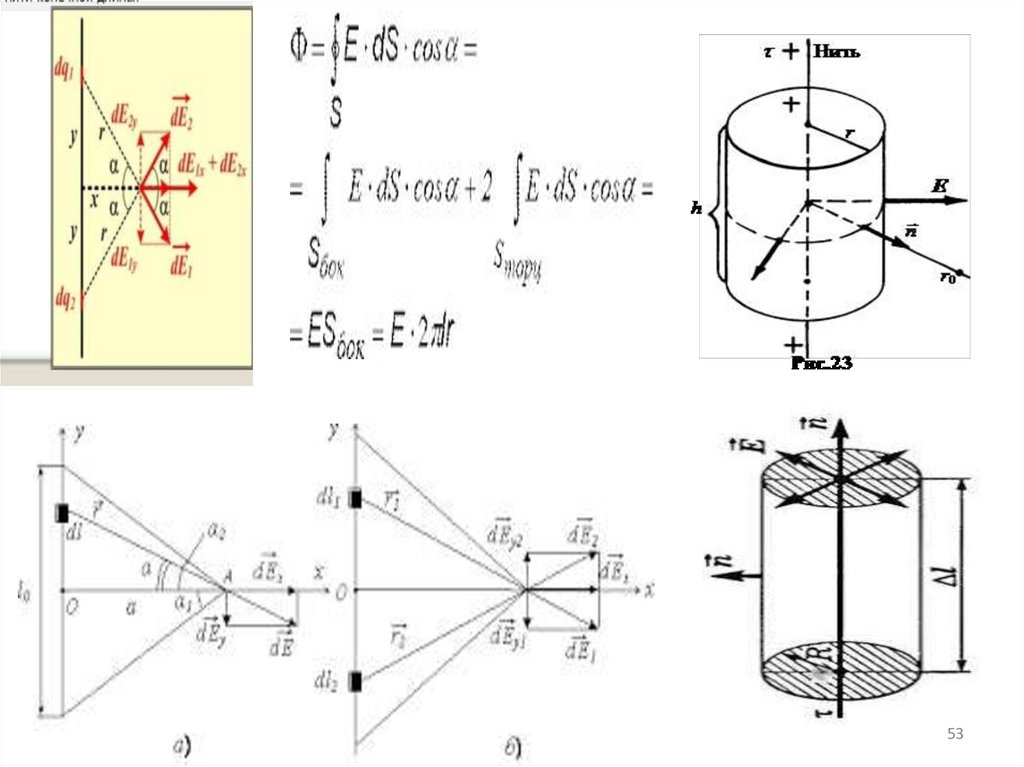
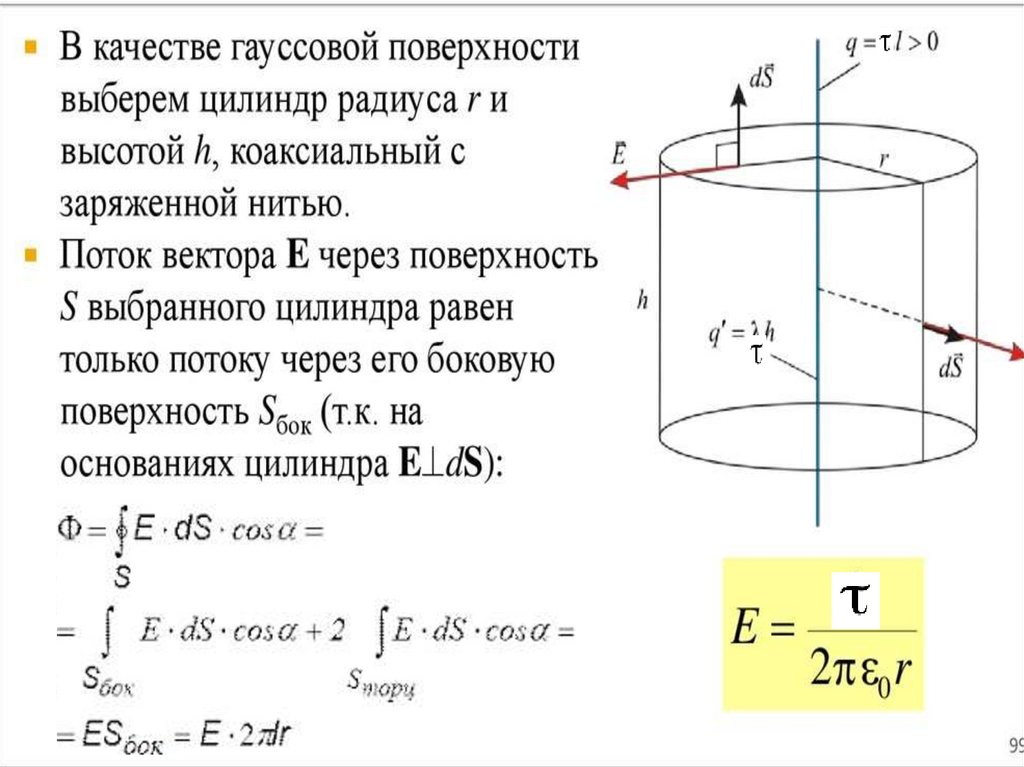
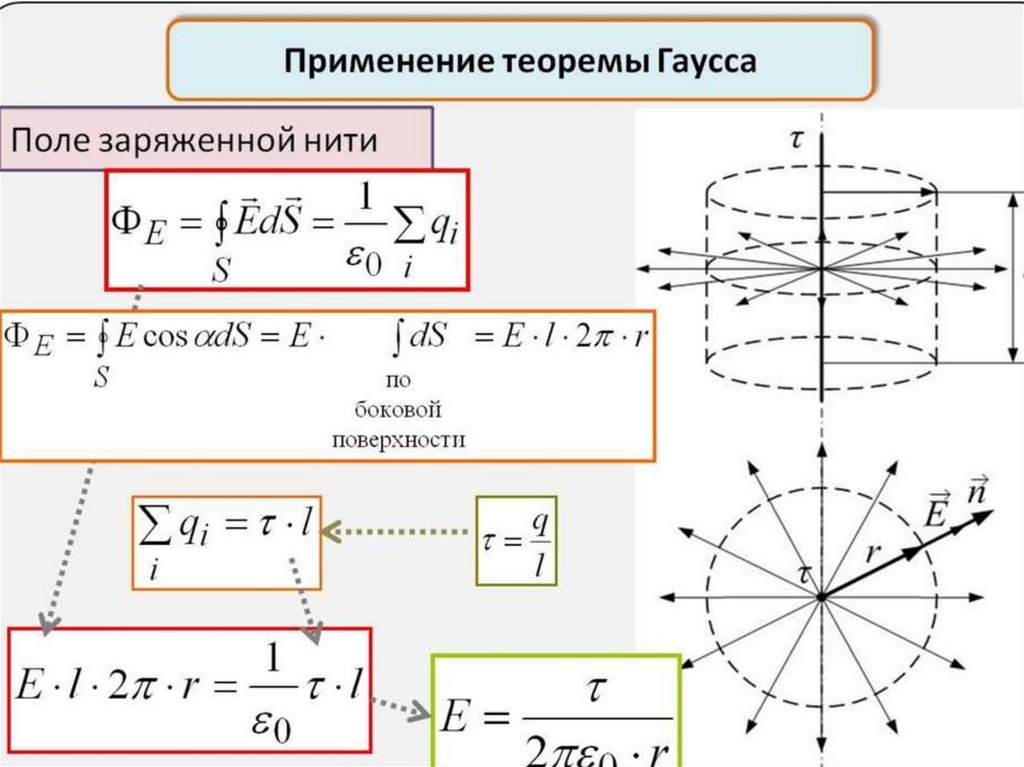
В Международной системе СИ за единицу
заряда принят кулон (Кл)-заряд,
проходящий за 1 с через поперечное сечение
проводника при силе тока в 1А
8

9.

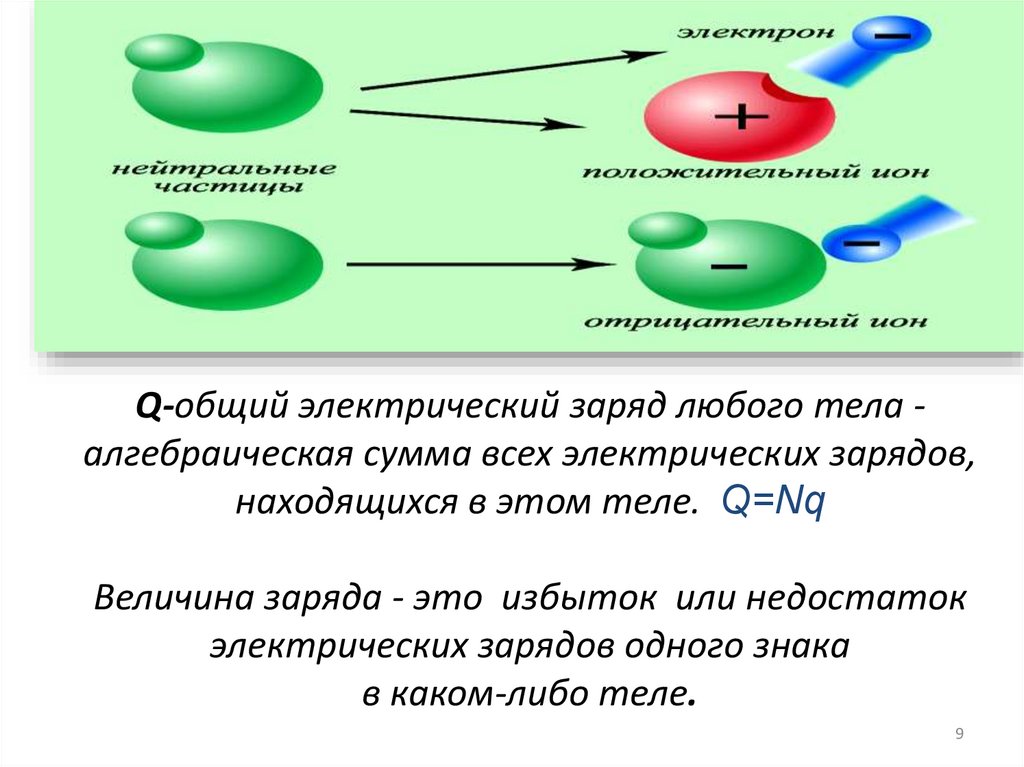
Q-общий электрический заряд любого тела алгебраическая сумма всех электрических зарядов,
находящихся в этом теле. Q=Nq
Величина заряда - это избыток или недостаток
электрических зарядов одного знака
в каком-либо теле.
9

10.

10

11.

Элементарный заряд – минимальный заряд, которым
обладают элементарные частицы ( q ).
- Электрон имеет наименьший отрицательный
электрический заряд, существующий в природе:
q = e = - 1,6 • 10 -19 Кл
- Протон имеет наименьший положительный
электрический заряд: q = +1,6 • 10 -19 Кл
Точечный заряд - заряд сосредоточенный на теле,
линейные размеры которого значительно меньше
расстояния до других заряженных тел.
Пробный заряд - небольшой по величине точечный
положительный заряд, используемый для обнаружения и
исследования электростатического поля, qо.
11

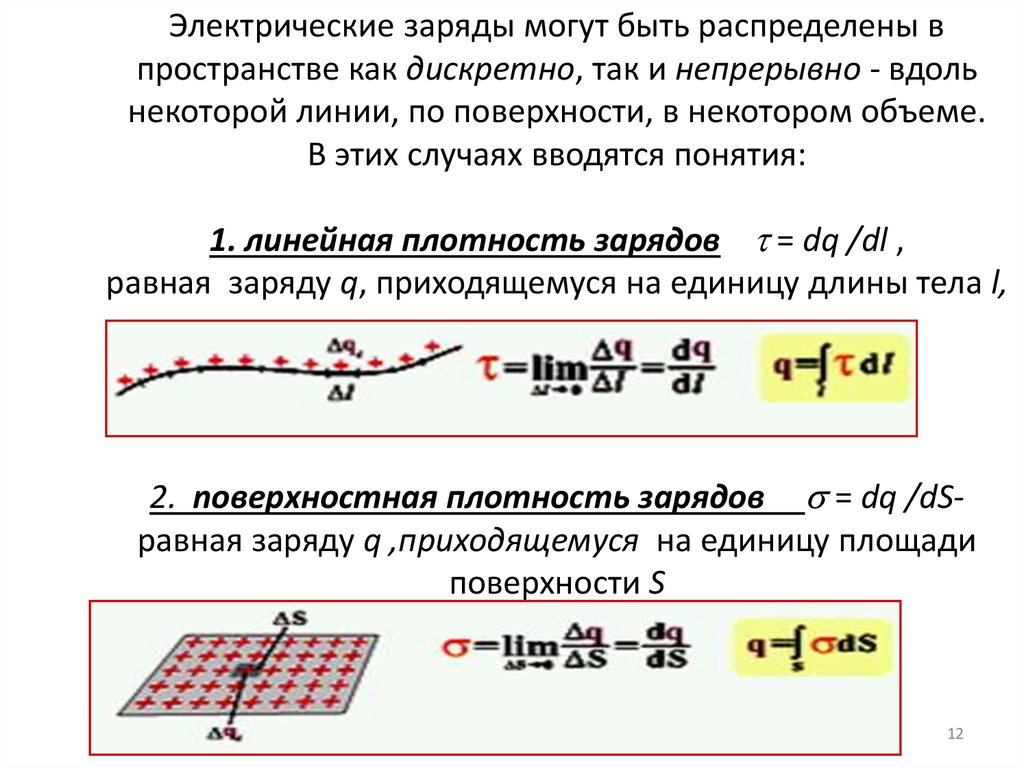
12. Электрические заряды могут быть распределены в пространстве как дискретно, так и непрерывно - вдоль некоторой линии, по

поверхности, в некотором объеме.
В этих случаях вводятся понятия:
1. линейная плотность зарядов = dq /dl ,
равная заряду q, приходящемуся на единицу длины тела l,
2. noверxнocтная плотность зарядов = dq /dSравная заряду q ,приходящемуся на единицу площади
поверхности S
12

13.

3. объемная плотность зарядов
= dq/dV ,
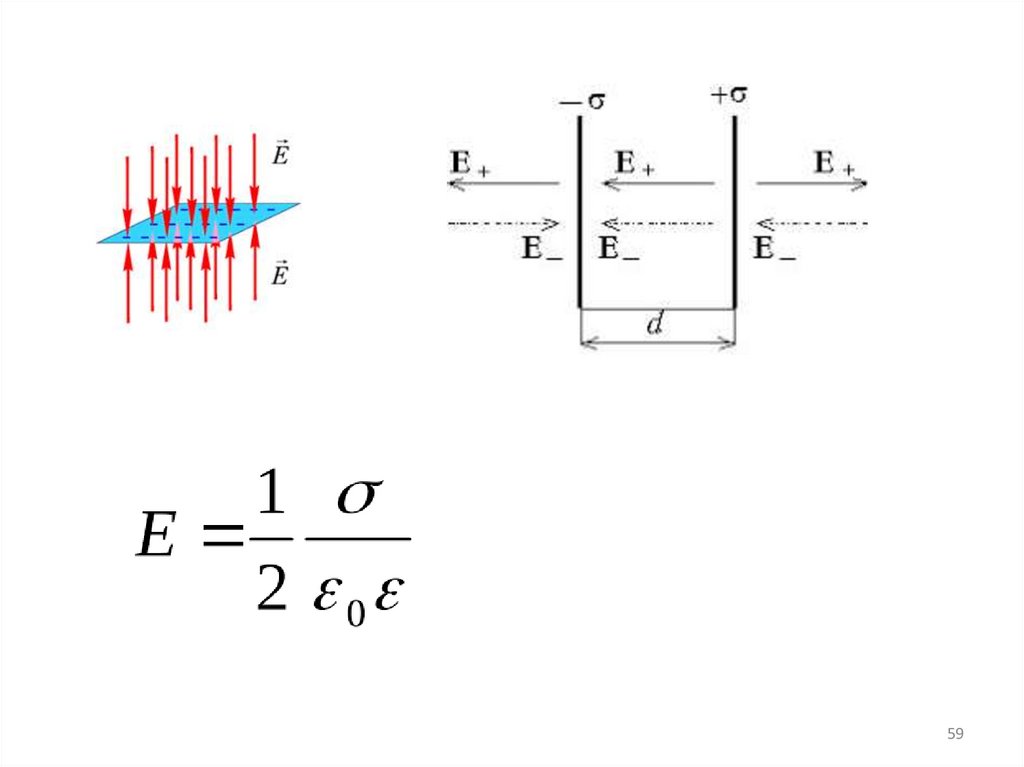
которая равна заряду q, приходящемуся на единицу
объема тела V.
13

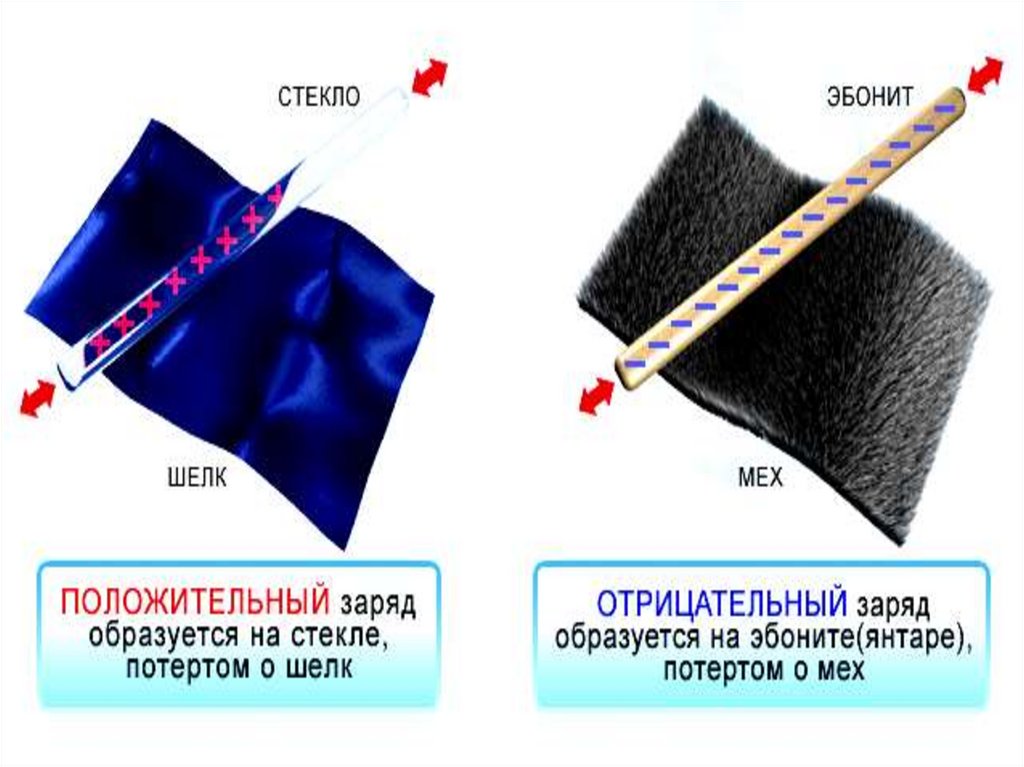
14. Свойства электрических зарядов

Электрический заряд
cуществует в двух видах:
Положительный
Отрицательный
1. Электрический заряд и н в а р и а н т е н (его величина не зависит
от системы отсчета, т. е. от того, движется он или покоится).
2. Электрический заряд д и с к р е т е н, т. е. заряд любого
тела составляет целое кратное элементарного электрического
заряда q. Q=Nq
3. Электрический заряд а д д и т и в е н (заряд любой системы
частиц (тел) равен сумме зарядов частиц (тел ), входящих в систему).
4. Электрический заряд замкнутой системы тел п о с т о я н е н.
5. Одноименные заряды отталкиваются , разноименные –
притягиваются
14

15. Закон сохранения электрического заряда

В замкнутой системе взаимодействующих тел
алгебраическая сумма электрических зарядов
(полный электрический заряд) остается неизменной
при всех взаимодействиях.
Заряды могут появляться и исчезать только парами. В
целом Вселенная нейтральна
15

16. Закон Кулона

Закон Кулона - основной закон
электростатики, выражающий
зависимость силы взаимодействия двух
неподвижных точечных зарядов в
вакууме от расстояния между ними.
Дает возможность
определить силу
(кулоновского)
взаимодействия между
неподвижными
заряженными телами.
Справедлив только для
точечных зарядов.
16

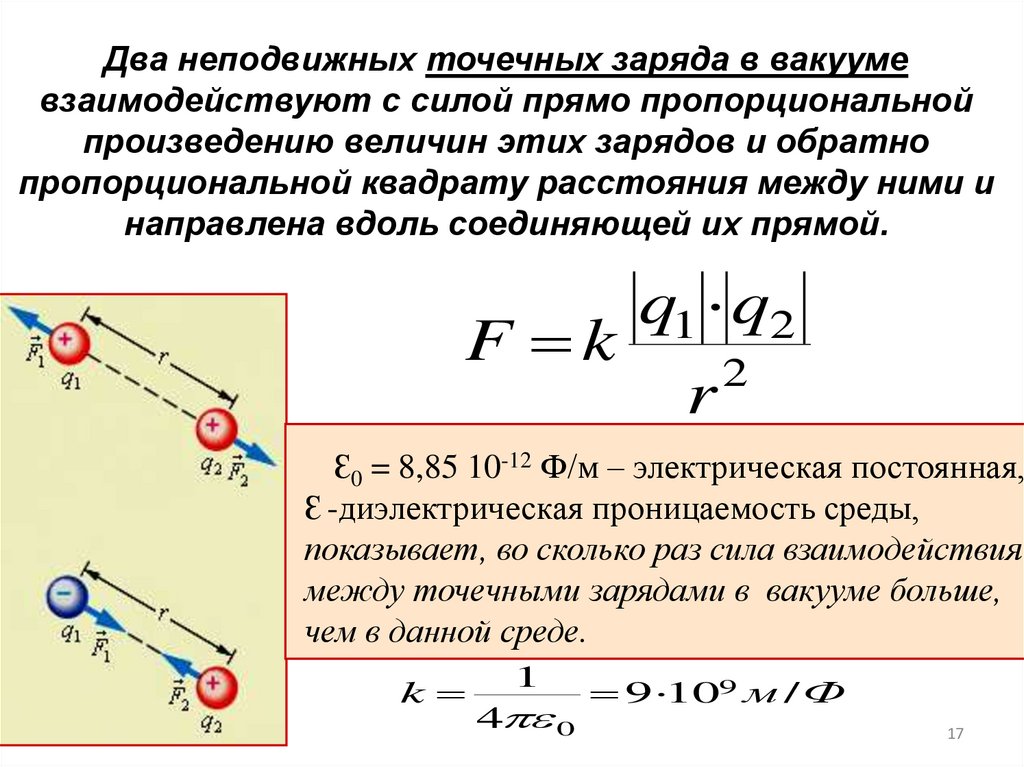
17.

Два неподвижных точечных заряда в вакууме
взаимодействуют с силой прямо пропорциональной
произведению величин этих зарядов и обратно
пропорциональной квадрату расстояния между ними и
направлена вдоль соединяющей их прямой.
q1 q2
F k
2
r
Ԑ0 = 8,85 10-12 Ф/м – электрическая постоянная,
Ԑ -диэлектрическая проницаемость среды,
показывает, во сколько раз сила взаимодействия
между точечными зарядами в вакууме больше,
чем в данной среде.
k
1
4 0
9 109 м / Ф
17

18.

Если электрические заряды поместить внутрь диэлектрика,
то сила электрического взаимодействия уменьшается в
соответствии с выражением:
В веществе
q1 q2
F k
2
r
ε─ диэлектрическая проницаемость
среды (безразмерная величина ),
показывающая, во сколько раз сила
взаимодействия в данной среде
меньше чем в вакууме).
Вещество
ε
Вода
81
Керосин
2
Масло
5
Эбонит
2,6
Слюда, стекло
7
18

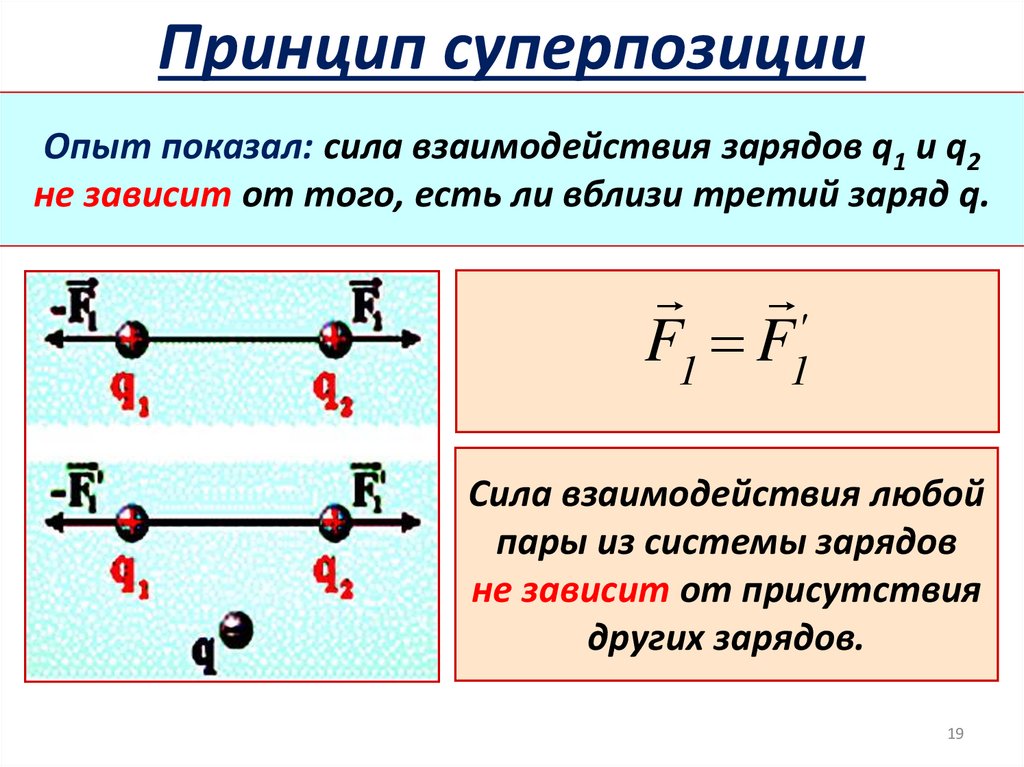
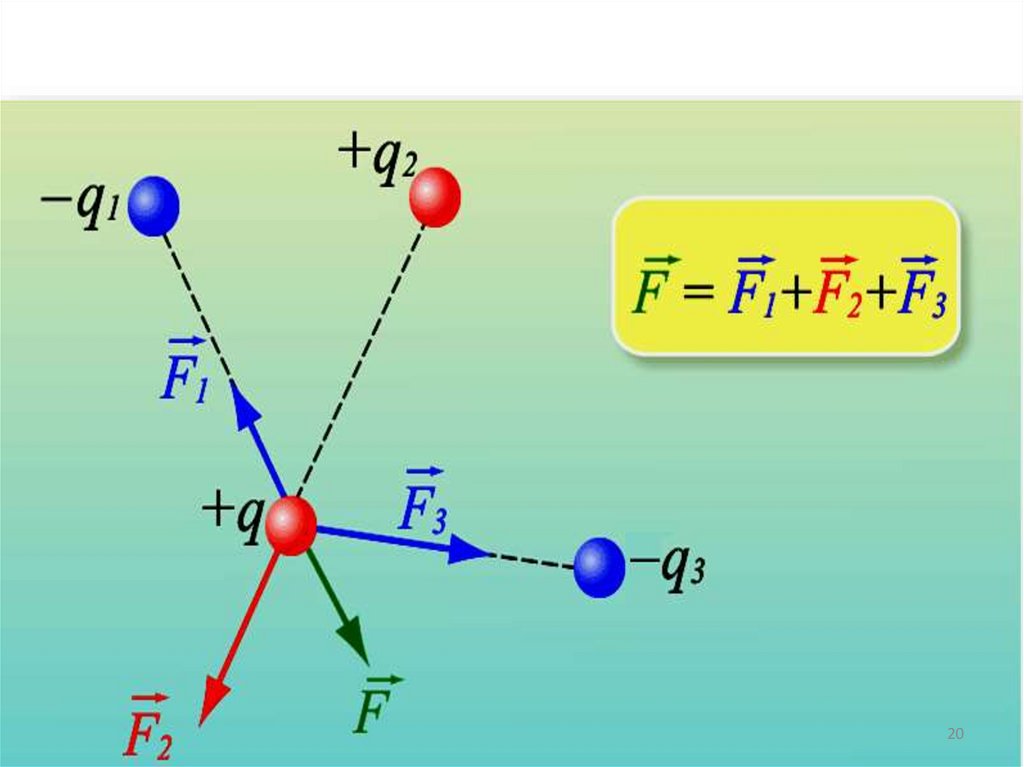
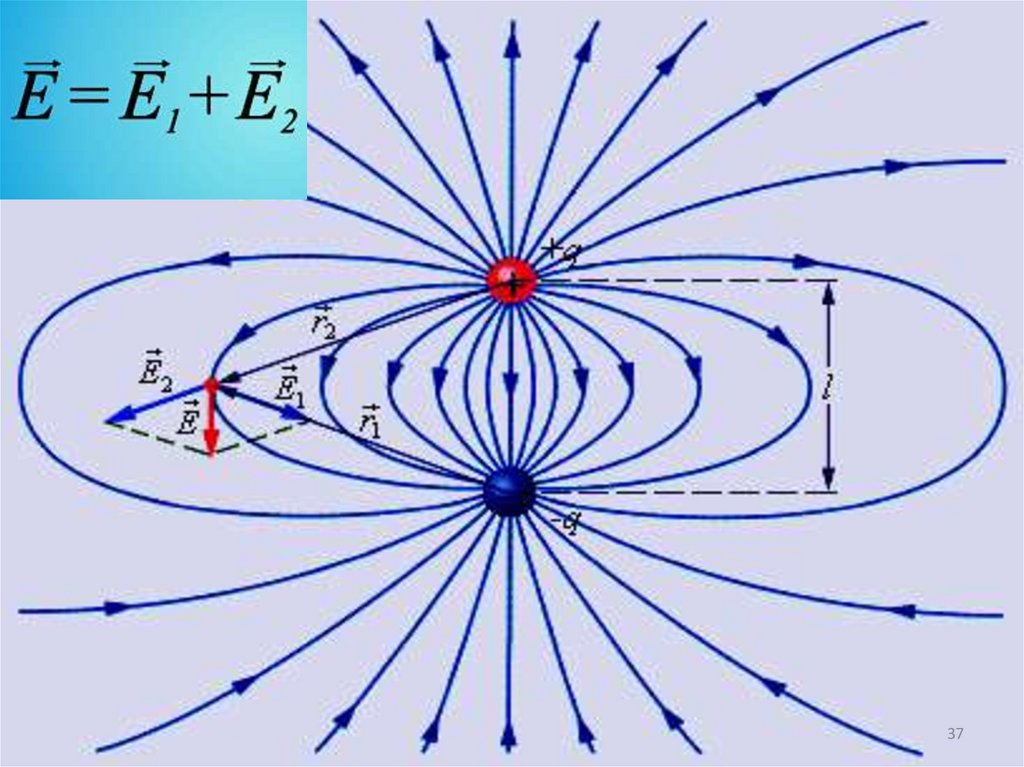
19. Принцип суперпозиции

Опыт показал: сила взаимодействия зарядов q1 и q2
не зависит от того, eсть ли вблизи третий заряд q.
F1 F1'
Сила взаимодействия любой
пары из системы зарядов
не зависит от присутствия
других зарядов.
19

20.

20

21.

Электрический заряд q вносит изменение
в окружающее пространство.
Вокруг любого заряда образуется и
распространяется электрическое поле.
21

22.

В настоящее время, исходят из представления, что
взаимодействия зарядов передаются с помощью особого
материального посредника, называемого электрическим полем.
Взаимодействие двух зарядов q1 и q2 можно объяснить так: в
пространстве вокруг заряда q1 существует особая форма материи
– электрическое поле, которое и действует непосредственно на
заряд q2. Действие электрического поля на помещенный в него
заряд является основным его свойством.
Далее речь пойдет об электрических полях, созданных
неподвижными
зарядами.
Такие
поля
называются
электростатическими. Для простоты изложения условимся в
дальнейшем под словом «поле», «электрическое поле» понимать
электростатическое поле, т.е. поле, созданное неподвижными
зарядами.
Для описания каждой точки электрического поля вводятся
две характеристики – напряженность электрического поля Е и
потенциал .
22

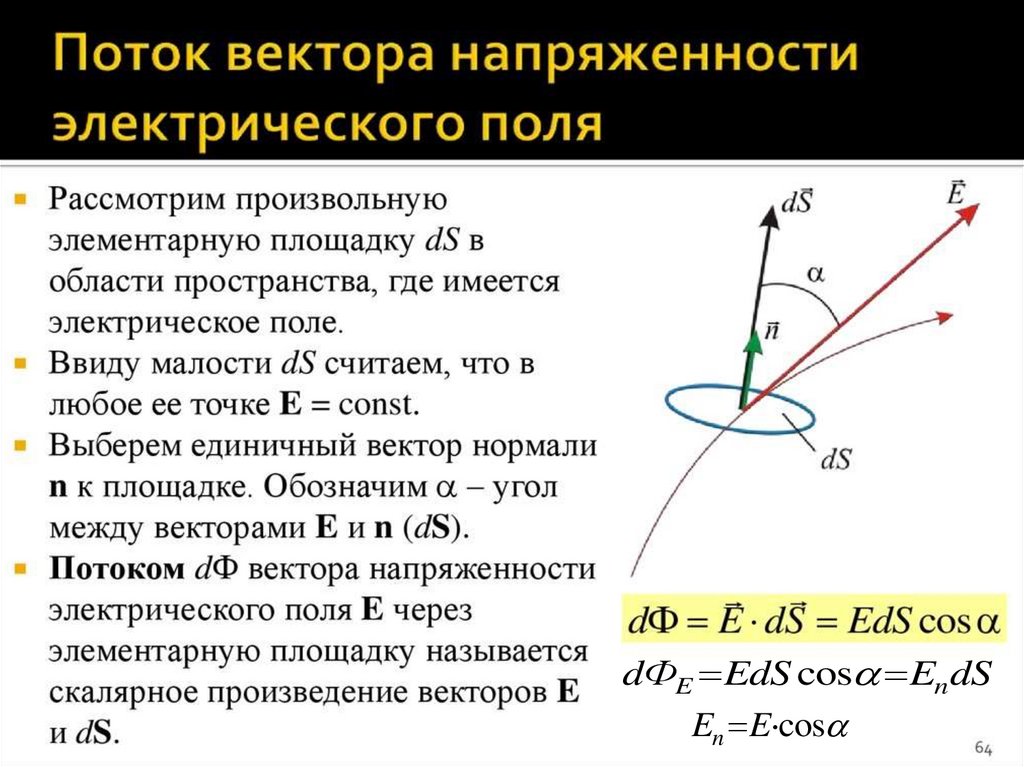
23. Основные характеристики электростатического поля 1. Напряженность электрического поля ( E ) – силовая характеристика 2.

Потенциал ( )
- энергетическая характеристика
23

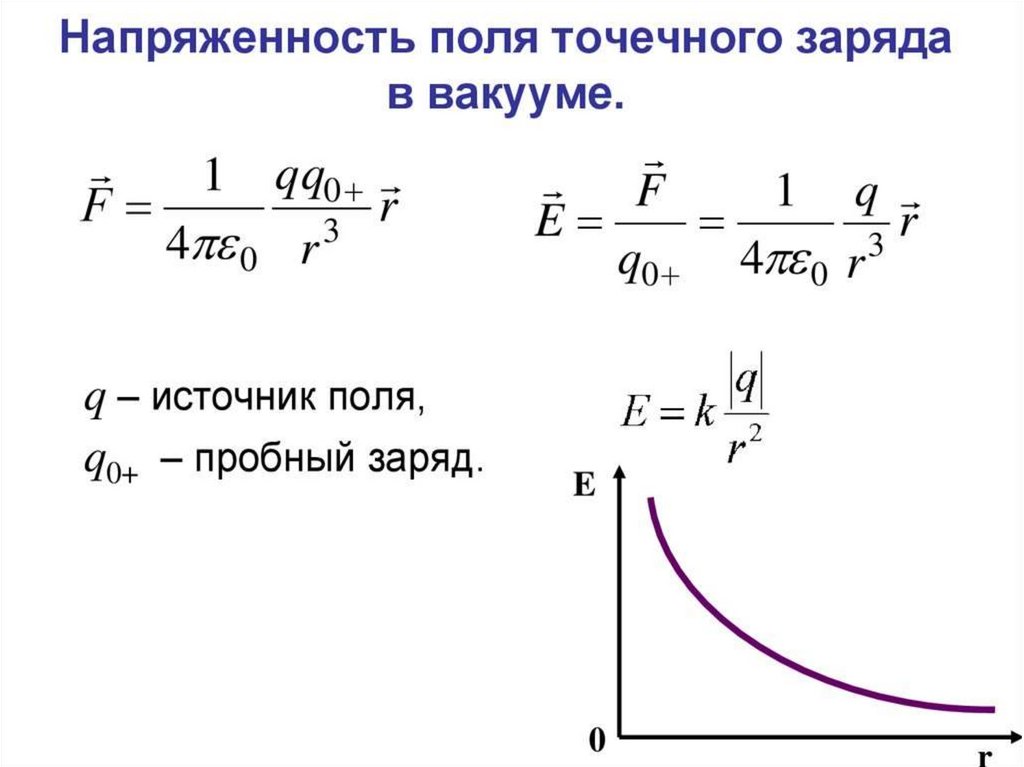
24. 1. Напряженность электростатического поля

Каждое заряженное тело создает в
окружающем пространстве электрическое
поле. Взаимодействие заряженных тел
осуществляется через электрические поля,
окружающие заряженные тела.
• Для количественного определения
электрического поля вводится силовая
характеристика – напряженность
электрического поля E
24

25.

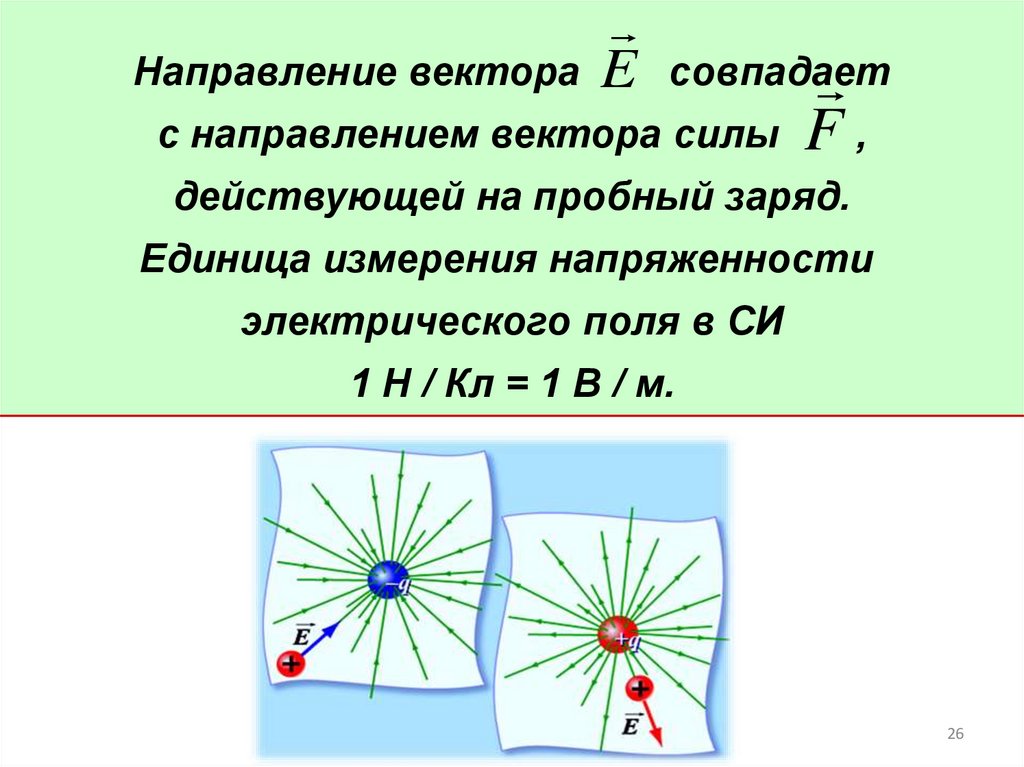
Напряженность электрического поля E :
- сила, с которой поле действует на единичный
положительный заряд ;
- совпадает по направлению с силой, действующей
на частицу с положительным зарядом.
25

26.

Направление вектора E совпадает
с направлением вектора силы F ,
действующей на пробный заряд.
Единица измерения напряженности
электрического поля в СИ
1 Н / Кл = 1 В / м.
26

27. Для характеристики электрического поля в различных средах наряду с вектором напряженности электрического поля вводится величина

Для характеристики электрического поля в
различных средах наряду с вектором
напряженности электрического поля E
вводится величина – электрическое
смещение (электрическая индукция) D ,
которая связана с Е соотношением
D = ε 0 εE
Здесь ε -электрическая проницаемость
вещества, характеризующая способность
вещества создавать электрическое поле под
действием внешнего электрического поля.
27

28.

29. Принцип суперпозиции

Если с помощью пробного заряда исследуется
электрическое
поле,
создаваемое
несколькими
заряженными телами, то результирующая сила
оказывается равной геометрической сумме сил,
действующих на пробный заряд со стороны каждого
заряженного тела в отдельности.
Следовательно, напряженность электрического поля,
создаваемого системой зарядов в данной точке
пространства,
равна
векторной
сумме
напряженностей электрических полей, создаваемых в
той же точке зарядами в отдельности:
Это свойство электрического поля означает, что поле
подчиняется принципу суперпозиции.

30.

30

31.

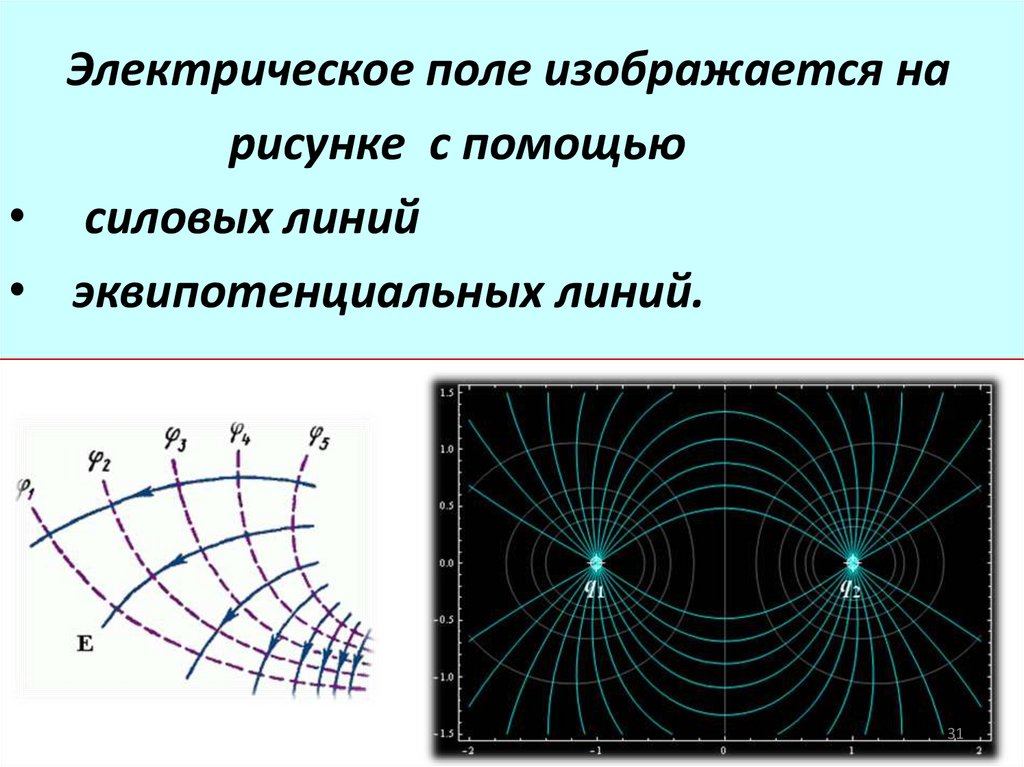
Электрическое поле изображается на
рисунке с помощью
• силовых линий
• эквипотенциальных линий.
31

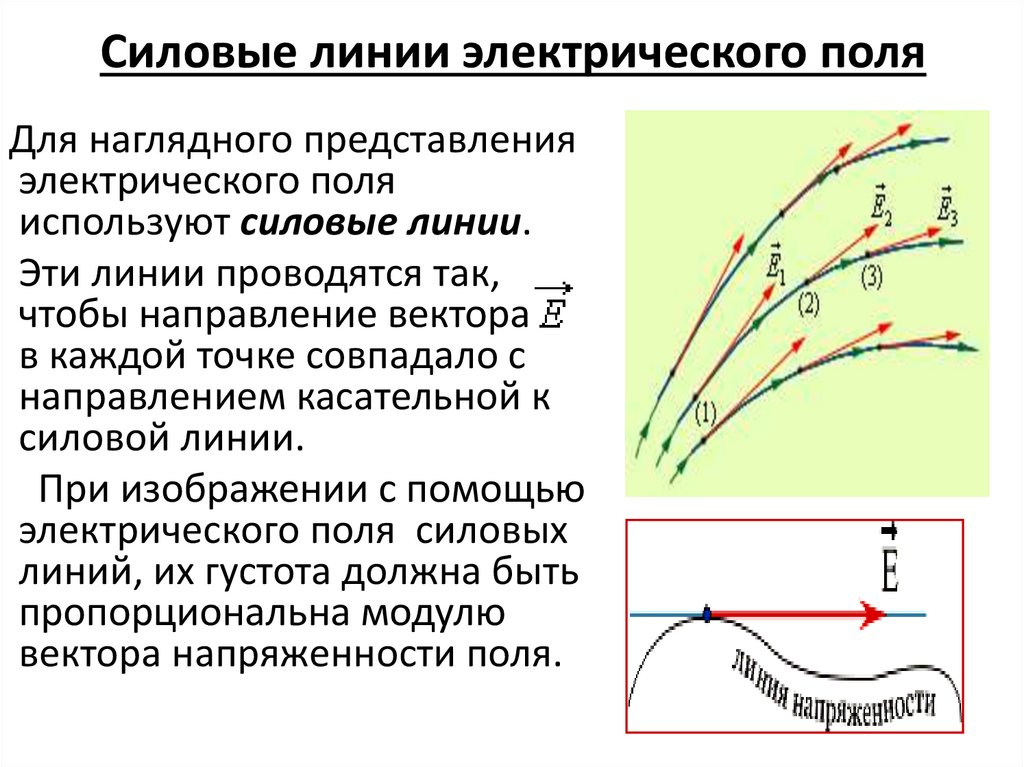
32. Силовые линии электрического поля

Для наглядного представления
электрического поля
используют силовые линии.
Эти линии проводятся так,
чтобы направление вектора
в каждой точке совпадало с
направлением касательной к
силовой линии.
При изображении с помощью
электрического поля силовых
линий, их густота должна быть
пропорциональна модулю
вектора напряженности поля.

33.

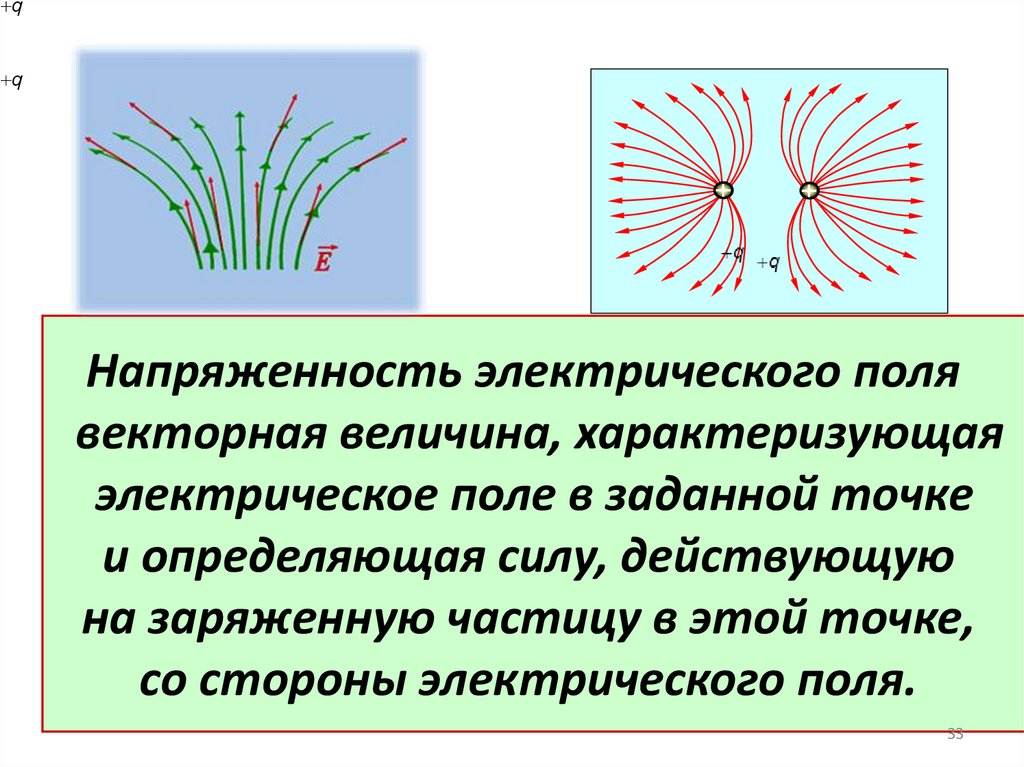
q
q
Напряженность электрического поля
векторная величина, характеризующая
электрическое поле в заданной точке
и определяющая силу, действующую
на заряженную частицу в этой точке,
со стороны электрического поля.
33

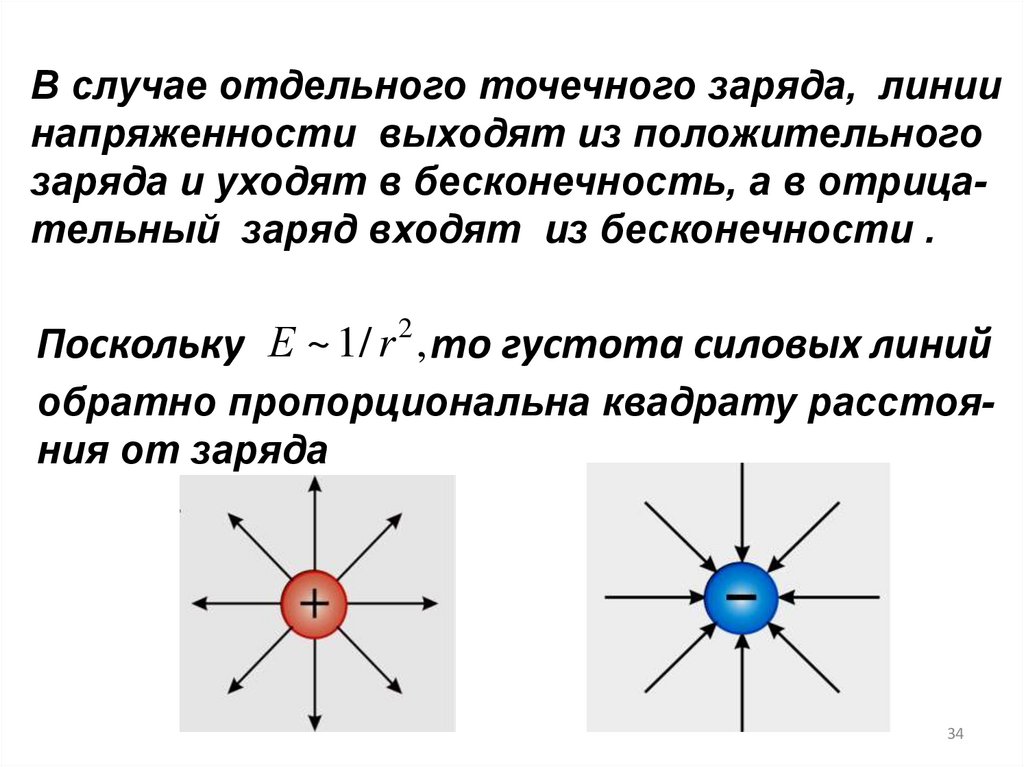
34.

В случае отдельного точечного заряда, линии
напряженности выходят из положительного
заряда и уходят в бесконечность, а в отрицательный заряд входят из бесконечности .
2
Е
~
1
/
r
, то густота силовых линий
Поскольку
обратно пропорциональна квадрату расстояния от заряда
34

35.

35

36.

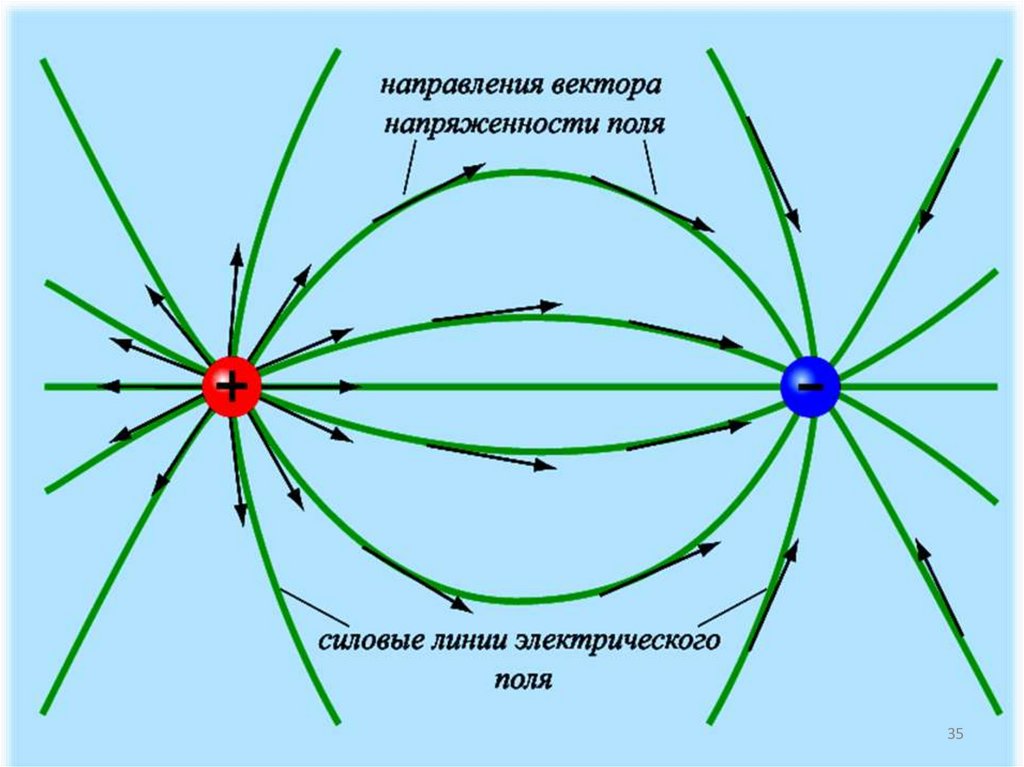
Свойства силовых линий
электрического поля:
1. Силовые поля начинаются на положительных
зарядах или в бесконечности и заканчиваются на
отрицательных зарядах или в бесконечности .
2. Силовые линии электрического поля нигде не
пересекаются.
3. Густота проведения силовых линий должна быть
такой, чтобы число силовых линий через площадку
1м2, расположенную перпендикулярно к каждой
силовой линии, было численно равно значению
модуля вектора напряженности в данной точке.
36

37.

37

38.

Однородным называется
электростатическое поле, во всех точках
которого напряженность одинакова по
величине и направлению.
Однородное электростатическое поле
изображается параллельными силовыми
линиями на равном расстоянии друг от друга.
38

39.

dФE EdS cos En dS
En E cos
39

40.

40

41.

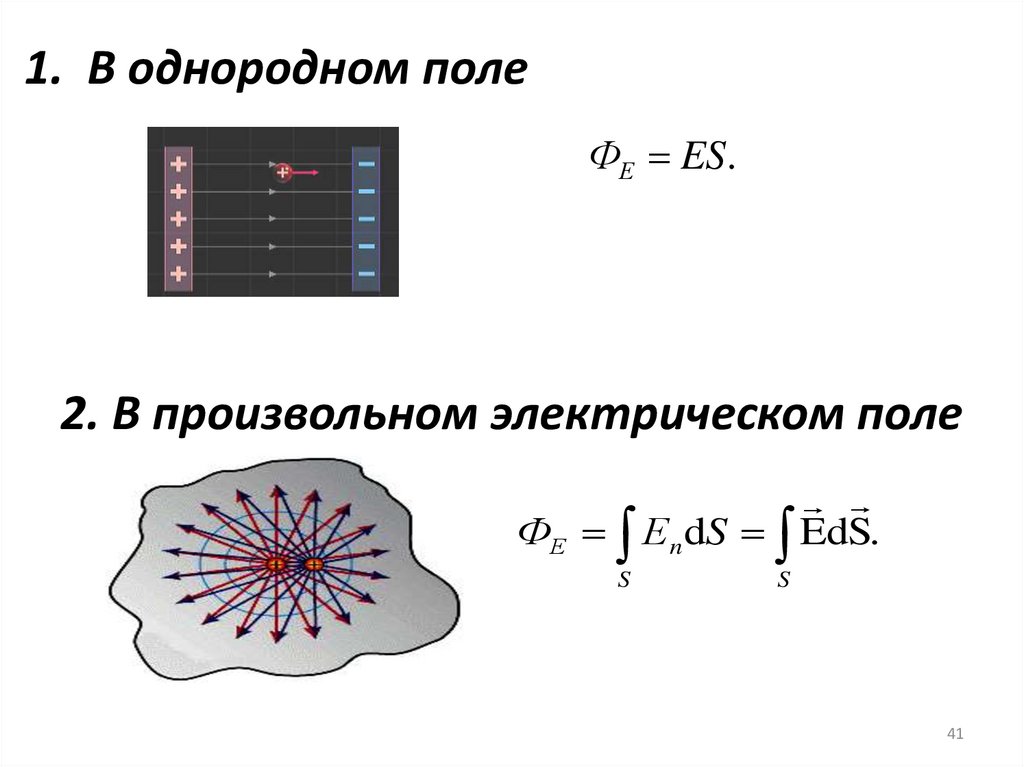
1. В однородном поле
ФЕ ES.
2. В произвольном электрическом поле
ФЕ Еn dS EdS.
S
S
41

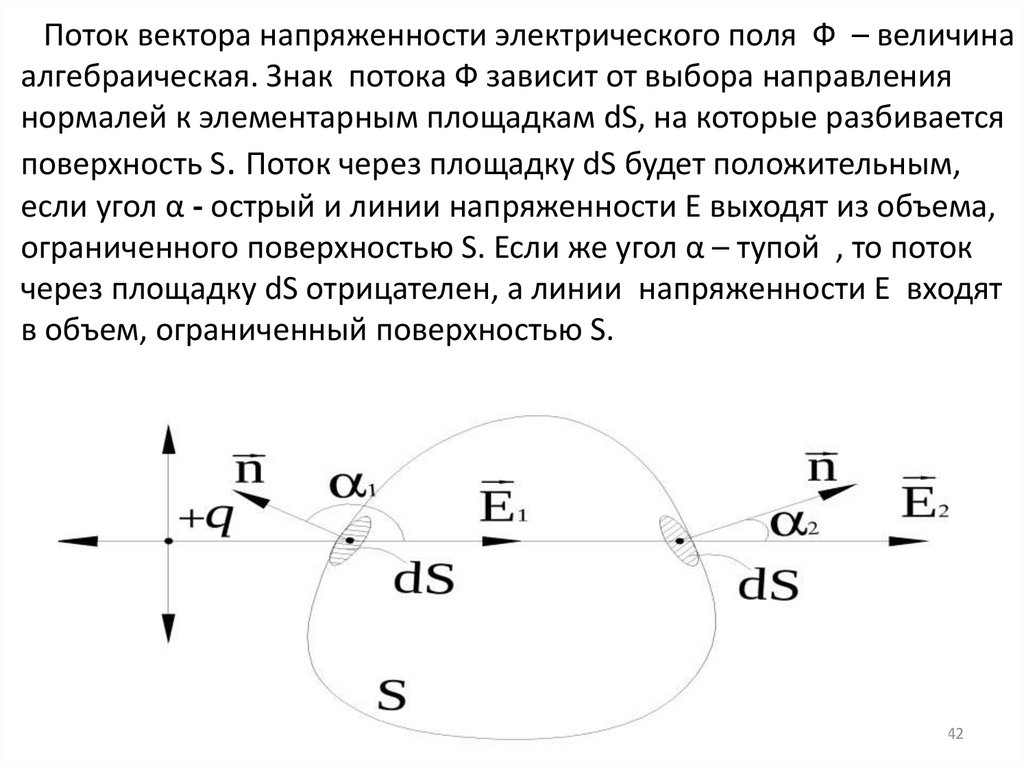
42. Поток вектора напряженности электрического поля Ф  – величина алгебраическая. Знак потока Ф зависит от выбора направления

Поток вектора напряженности электрического поля Ф – величина
алгебраическая. Знак потока Ф зависит от выбора направления
нормалей к элементарным площадкам dS, на которые разбивается
поверхность S. Поток через площадку dS будет положительным,
если угол α - острый и линии напряженности Е выходят из объема,
ограниченного поверхностью S. Если же угол α – тупой , то поток
через площадку dS отрицателен, а линии напряженности Е входят
в объем, ограниченный поверхностью S.
42

43.

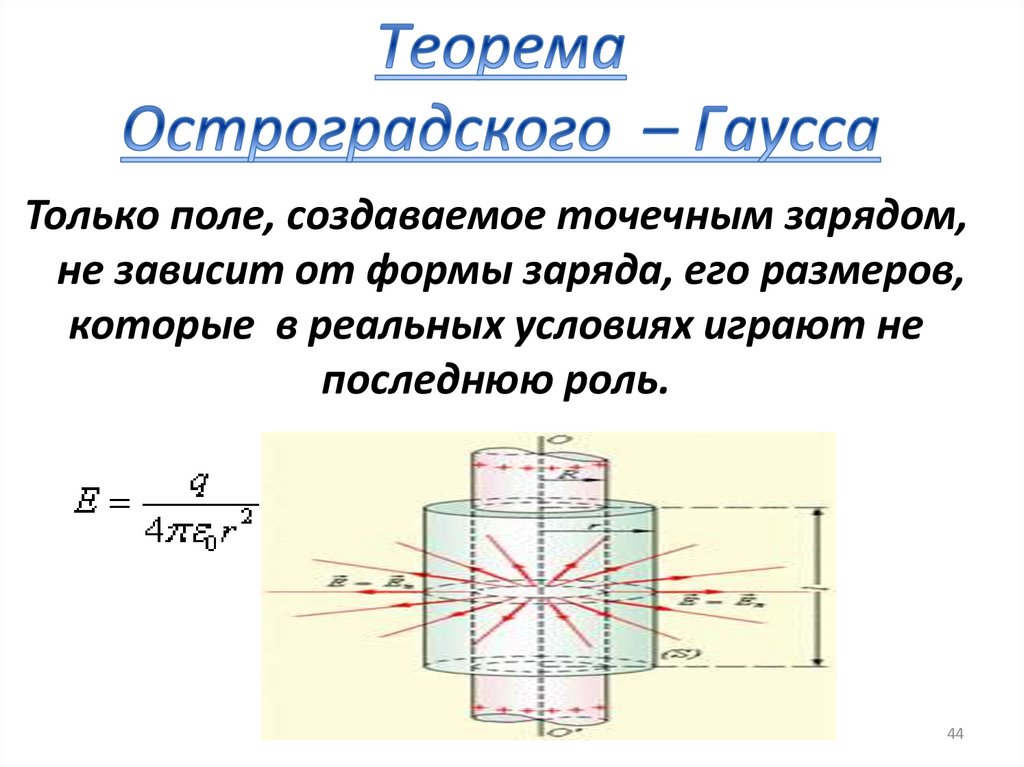
43

44.

Только поле, создаваемое точечным зарядом,
не зависит от формы заряда, его размеров,
которые в реальных условиях играют не
последнюю роль.
44

45. Т Теорема Гаусса устанавливает связь между потоком ФЕ вектора напряженности через произвольную замкнутую поверхность S и

•Теорема Гаусса устанавливает связь между потоком
Ф вектора напряженности через произвольную
Е
замкнутую поверхность S и суммарным
электрическим зарядом, находящимся в объеме,
ограниченном этой поверхностью.

46.

Поток вектора напряженности
электрического поля через произвольную
замкнутую поверхность равен
алгебраической сумме зарядов, охваченных
этой поверхностью
(ε0 =8,85*10-12 ф/м)
ФE En dS
S
1
0
qi
46

47. Если поле создано системой зарядов, то под q следует понимать алгебраическую сумму зарядов, охватываемых поверхностью S: В

Если поле создано системой зарядов, то
под q следует понимать алгебраическую сумму
зарядов, охватываемых поверхностью S:
В случае, когда заряды, охватываемые
поверхностью S, распределены непрерывно, то
q вычисляется как :
где , σ, ρ – соответственно линейная, поверхностная, объемная плотности зарядов
47

48. При использовании теоремы Остроградского – Гаусса для расчета электростатических полей нужно:

1. выбрать замкнутую поверхность, удобную для
данного случая и проходящую через
рассматриваемую точку;
2. вычислить ФЕ через эту замкнутую поверхность;
3. вычислить алгебраическую сумму зарядов внутри
выбранной замкнутой поверхности;
4. подставить полученные выражения в теорему и
вывести формулу, по которой можно рассчитать
напряженность электрического поля Е.
48

49.

Гауссова поверхность – это некая воображаемая
оболочка, в которую мы заключаем интересующую
нас область пространства и по которой интегрируем. Она может быть любой формы, но для удобства
вычисления , стоит выбрать такую, чтобы
1) электрическое поле было либо перпендикулярно
ей, либо параллельно.
2) гауссова поверхность должна повторять симметрию рассматриваемой системы.
49

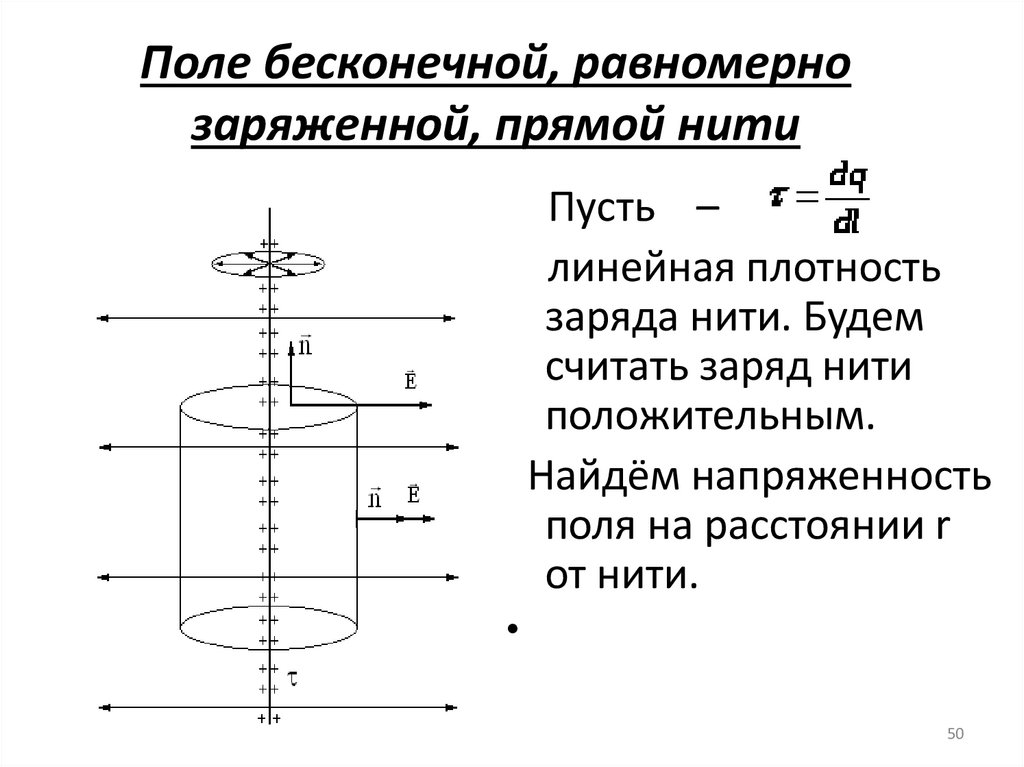
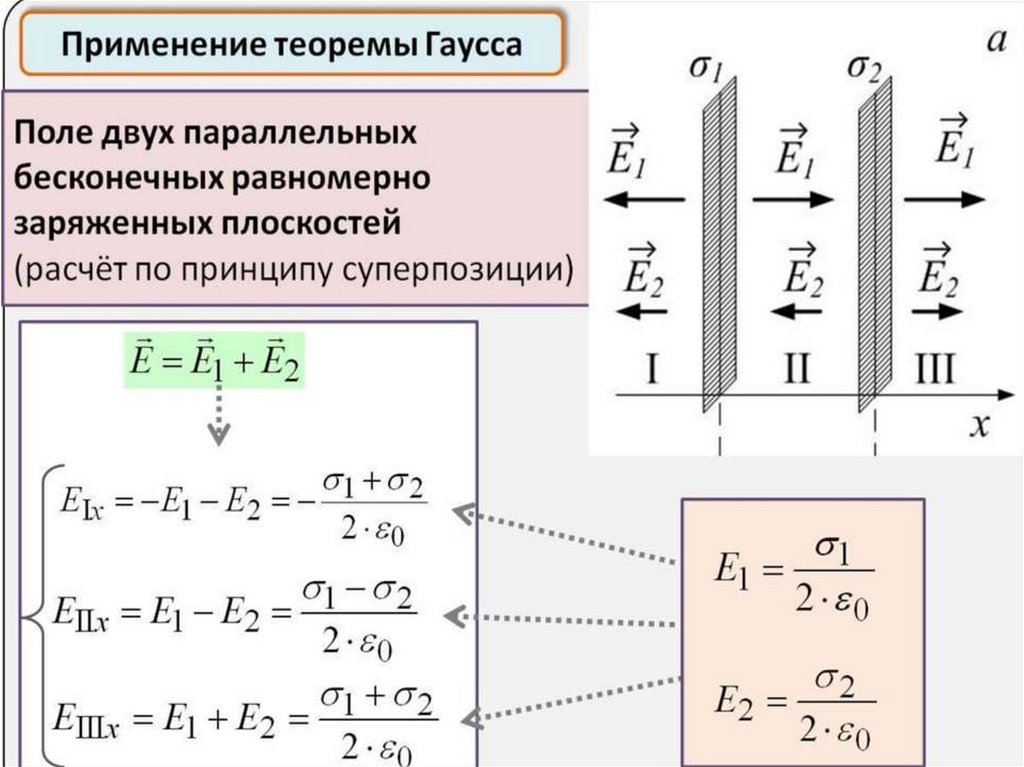
50. Поле бесконечной, равномерно заряженной, прямой нити

Пусть –
линейная плотность
заряда нити. Будем
считать заряд нити
положительным.
Найдём напряженность
поля на расстоянии r
от нити.
50

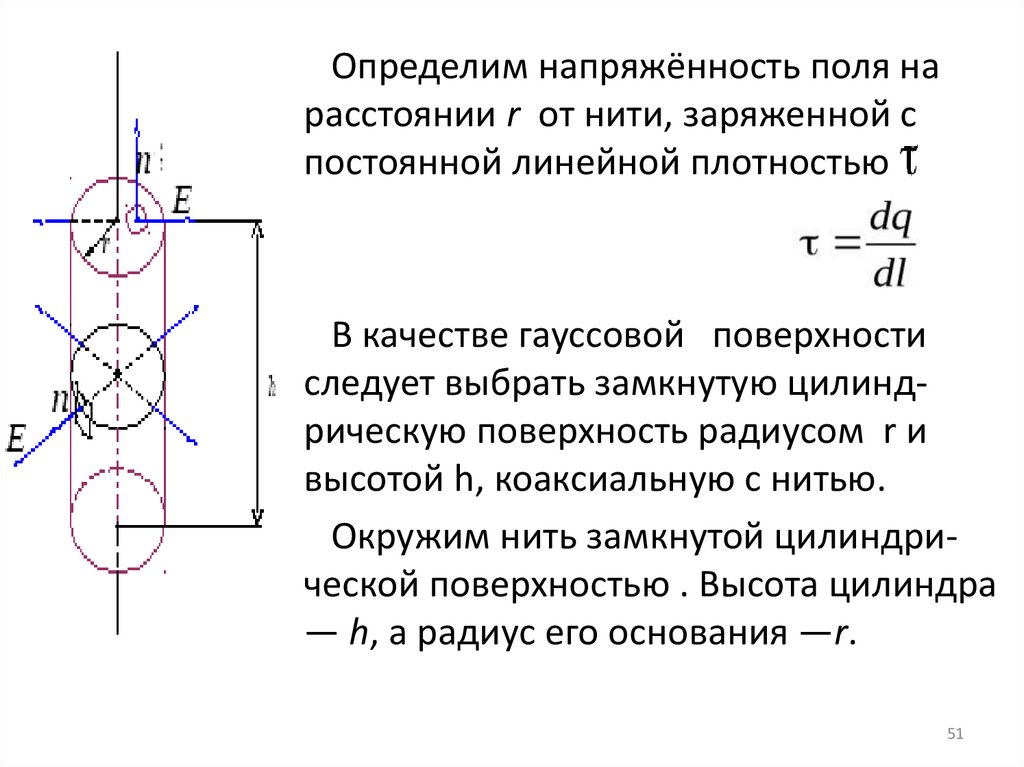
51.

Определим напряжённость поля на
расстоянии r от нити, заряженной с
постоянной линейной плотностью
В качестве гауссовой поверхности
следует выбрать замкнутую цилиндрическую поверхность радиусом r и
высотой h, коаксиальную с нитью.
Окружим нить замкнутой цилиндрической поверхностью . Высота цилиндра
— h, а радиус его основания —r.
51

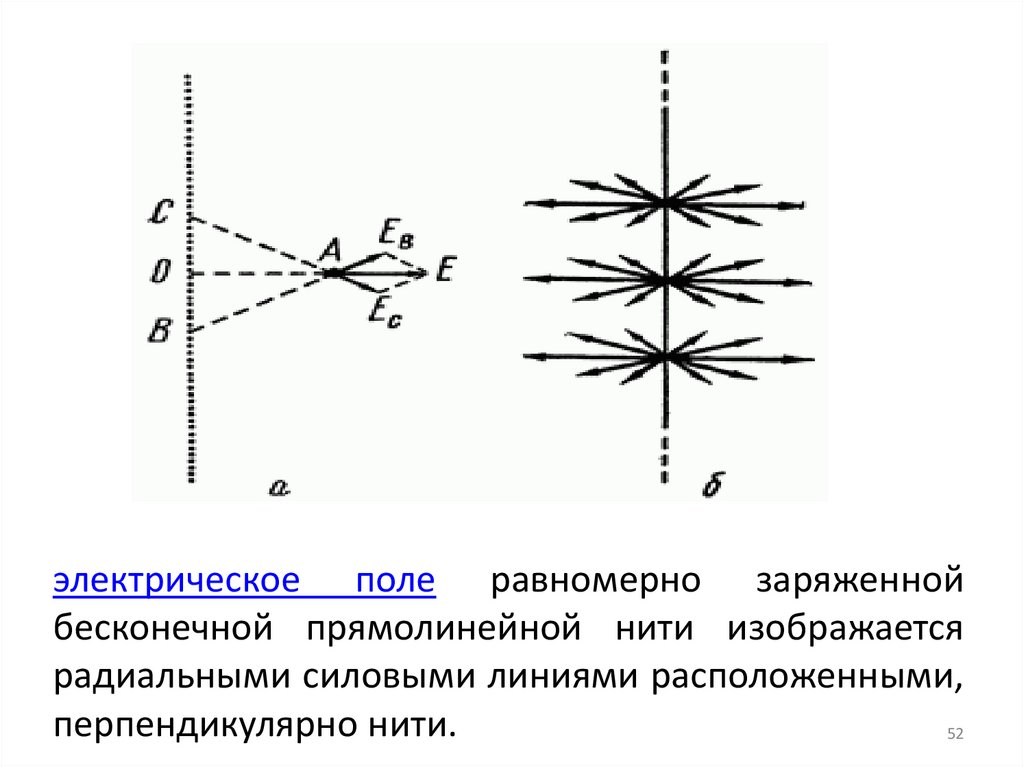
52.

электрическое поле равномерно заряженной
бесконечной прямолинейной нити изображается
радиальными силовыми линиями расположенными,
перпендикулярно нити.
52

53.

53

54.

Поле, созданное заряженной нитью, обладает
цилиндрической симметрией. В связи с этим векторы
напряжённости Е во всех точках боковой поверхности
цилиндра будут одинаковы по модулю и направлены
радиально
то есть перпендикулярно к
боковой поверхности цилиндра. На основаниях
цилиндра векторы, направленные по-прежнему
радиально, «скользят» по основанию, образуя прямой
угол с нормалью
.
Вычислим поток вектора
через поверхность
выбранного цилиндра. Полный поток через эту
замкнутую «гауссову» поверхность складывается из
потока через боковую поверхность цилиндра и через
два его основания.
54

55.

55

56.

Последние два интеграла равны нулю, так как
«скользящие» по основаниям цилиндра векторы не
пронизывают их и не создают никакого потока.
Формально эти два интеграла равны нулю, так как
между векторами и прямой угол 90 градусов, таким
образом cos 90 =0
Во всех точках боковой поверхности цилиндра cos 0 =1.
Поэтому поток через боковую поверхность цилиндра
равен
56

57.

Теперь воспользуемся теоремой Гаусса, отметив
предварительно, что «заряд, заключённый внутри
гауссовой поверхности» в данном случае
сосредоточен на отрезке нити h— на оси цилиндра:
Таким образом
Отсюда теперь легко получить знакомую нам
гиперболическую зависимость напряжённости поля
от расстояния до нити — r
57

58.

58

59.

59

60.

60

61.

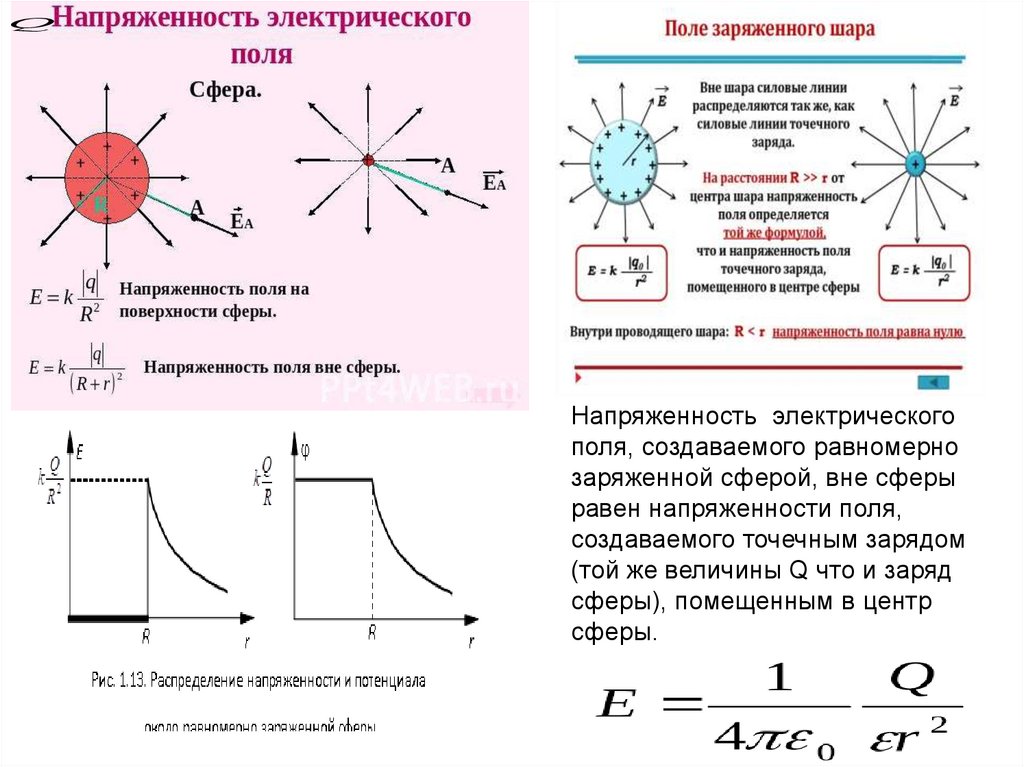
Q
Напряженность электрического
поля, создаваемого равномерно
заряженной сферой, вне сферы
равен напряженности поля,
создаваемого точечным зарядом
(той же величины Q что и заряд
сферы), помещенным в центр
сферы.

62.

Работа сил электрического поля
по перемещению заряда
На всякий заряд,
находящийся в
электрическом поле,
действует сила, и
поэтому при
движении заряда в
поле совершается
определенная
работа.
62

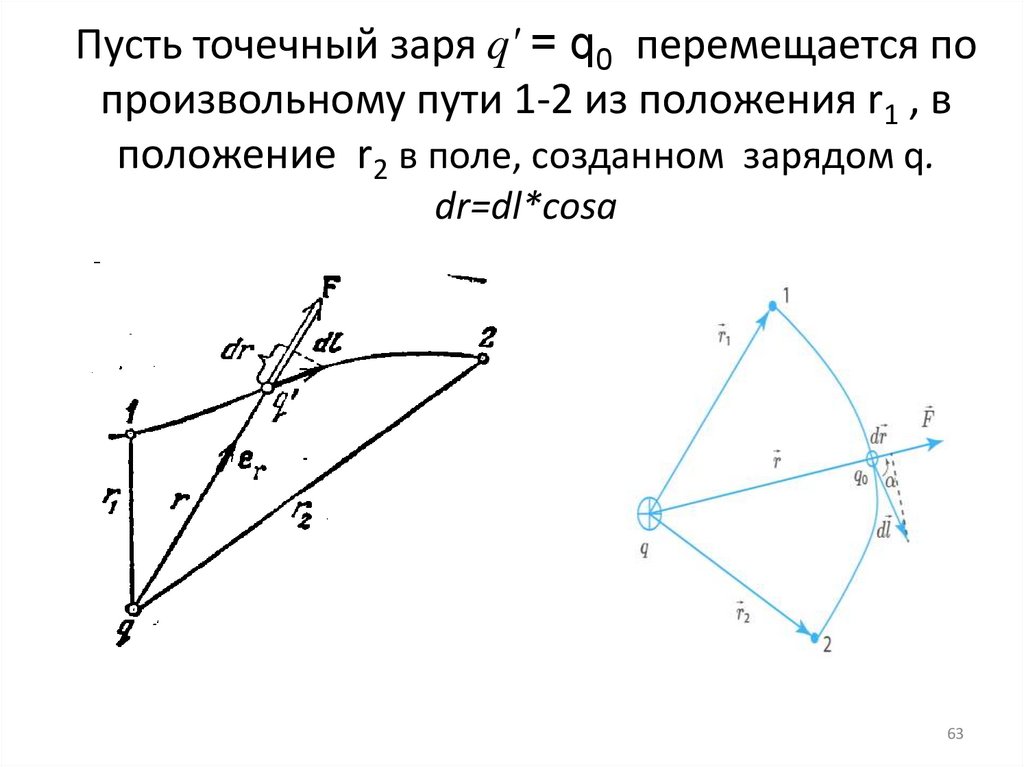
63. Пусть точечный заря q' = q0  перемещается по произвольному пути 1-2 из положения r1 , в положение  r2 в поле, созданном

Пусть точечный заря q' = q0 перемещается по
произвольному пути 1-2 из положения r1 , в
положение r2 в поле, созданном зарядом q.
dr=dl*cosɑ
63

64.

Элементарная работа, совершаемая силой F при
перемещении точечного электрического заряда q' = q0 из
точки 1 электрического поля в точку 2 на отрезке пути dℓ,
по определению, равна dA = Fdr= Fdℓcosα , где α - угол
между F и направлением движения. Подставим сюда
модуль силы F из закона Кулона
F=(q q' )/4πξ0r2
и, проинтегрировав выражение ,
Получим работу на участке 1-2:
64

65.

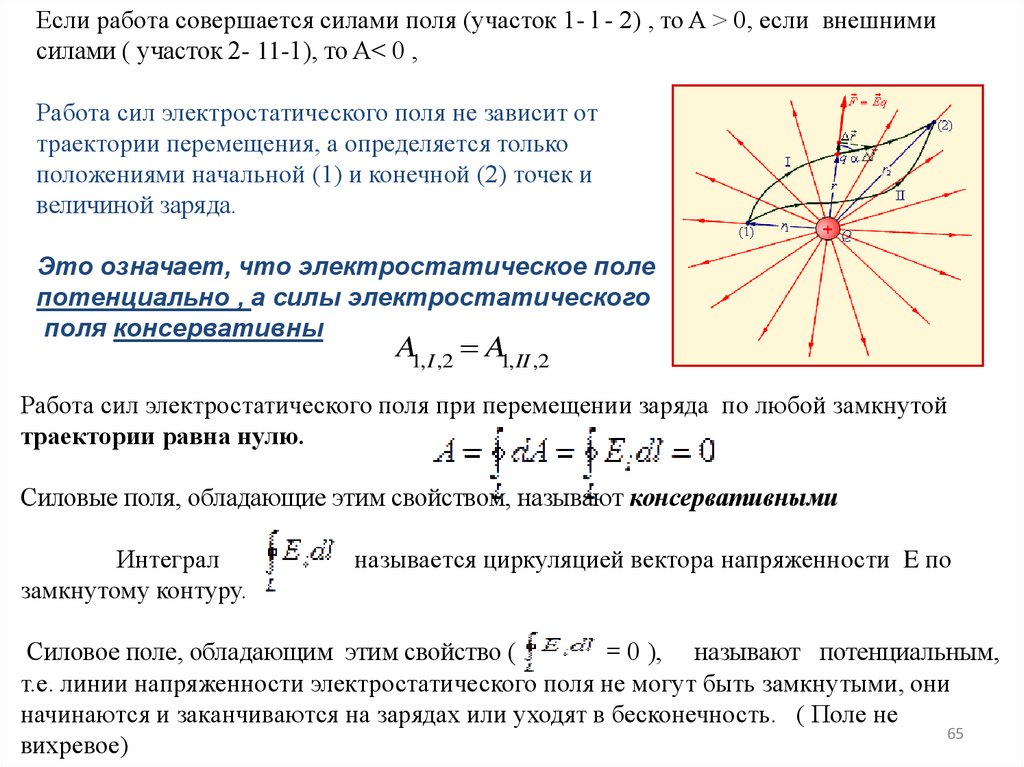
Если работа совершается силами поля (участок 1- l - 2) , то A > 0, если внешними
силами ( участок 2- 11-1), то A< 0 ,
Работа сил электростатического поля не зависит от
траектории перемещения, а определяется только
положениями начальной (1) и конечной (2) точек и
величиной заряда.
Это означает, что электростатическое поле
потенциально , а силы электростатического
поля консервативны
A1, I ,2 A1, II ,2
Работа сил электростатического поля при перемещении заряда по любой замкнутой
траектории равна нулю.
Силовые поля, обладающие этим свойством, называют консервативными
Интеграл
замкнутому контуру.
называется циркуляцией вектора напряженности E по
Силовое поле, обладающим этим свойство (
= 0 ), называют потенциальным,
т.е. линии напряженности электростатического поля не могут быть замкнутыми, они
начинаются и заканчиваются на зарядах или уходят в бесконечность. ( Поле не
65
вихревое)

66.

66

67. В теории физических полей существует общий принцип:

• если циркуляция вектора, служащего силовой
характеристикой поля, равна нулю, то такое
поле относится к классу потенциальных полей,
а если эта циркуляция не равна нулю, то такое
поле относится к классу вихревых полей.
• Таким образом, равенство нулю циркуляции
вектора напряженности электростатического
поля является признаком потенциальности
( консервативности) этого поля.
67

68.

• Электростатическое поле обладает важным свойством:
• Работа сил электростатического поля при перемещении
заряда из одной точки поля в другую не зависит от формы
траектории, а определяется только положением начальной
и конечной точек и величиной заряда.
Аналогичным свойством обладает и гравитационное поле, и в этом
нет ничего удивительного, так как гравитационные и
кулоновские силы описываются одинаковыми соотношениями.
Следствием независимости работы от формы траектории является
следующее утверждение:
• Работа сил электростатического поля при перемещении
заряда по любой замкнутой траектории равна нулю.
• Силовые поля, обладающие этим свойством,
называют потенциальными или консервативными.
68

69.

Свойство потенциальности электростатического поля
позволяет ввести понятие потенциальной энергии заряда в электрическом поле. В пространстве выбирается
некоторая точка (0), и потенциальная энергия заряда q,
помещенного в эту точку, принимается равной нулю.
Потенциальная энергия заряда q, помещенного в любую
точку (1) пространства, относительно фиксированной
точки (0) равна работе A1-0, которую совершит
электростатическое поле при перемещении заряда q из
точки (1) в точку (0): A1-0 = W1
Работа, совершаемая электростатическое полем при
перемещении точечного заряда q из точки (1) в точку (2),
равна разности значений потенциальной энергии в этих
точках и не зависит от пути перемещения заряда и от
выбора точки (0). A1-2 = -ΔWп =-(W2 - W1 ) = W1 - W2 69

70.

Работу сил электростатического поля можно
выразить через убыль потенциальной энергии –
разность двух функций состояний:
Это выражение для работы можно переписать в
виде:
, получаем
выражение для потенциальной энергии заряда
q' в поле заряда q:
Значение константы в выражения для W
выбирают таким образом, чтобы при удалении
заряда на бесконечность потенциальная энергия
обращалась в нуль.
70

71.

2. Потенциал электрического поля
Электростатический потенциа́л — скалярная энергетическая
характеристика электростатического поля, характеризующая
потенциальную энергию, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля
Потенциальная энергия заряда qпр в поле заряда q равна
Если поле создаётся системой n точечных зарядов q1, q2, …. qn, то
потенциальная энергия W зарядов qi , находящихся в этом поле,
равна сумме их потенциальных энергий Wi, создаваемых каждым из
зарядов в отдельности:
Исследуем с помощью пробного заряда (qпр)=q0 энергетическое
71
состояние электростатического поля.

72.

Потенциальная энергия W пробного заряда, внесённого в данную точку поля, зависит как от величины пробного заряда, так и
от свойств поля в этой точке.
Энергия же, отнесенная к единице пробного заряда W/qпр ,
зависит только от того, в какую точку помещён заряд. Следовательно, эта величина может служить характеристикой поля. Эта
величина называется потенциалом и является энергетической характеристикой электростатического поля.
Потенциал электростатического поля - скалярная физическая
величина, измеряемая отношением потенциальной энергии
пробного заряда в электростатическом поле к величине этого
заряда.
Она характеризует энергетическое состояние поля в данной
точке и равна потенциальной энергии, которой обладал бы
единичный, точечный, положительный заряд, помещённый в эту
точку. Поэтому потенциальная энергия точечного заряда q,
помещённого в точку поля с потенциалом φ равна
72
= Wп

73.

73

74. Принцип суперпозиции полей

Если поле создано несколькими зарядами, то
потенциал в любой точке поля равен
алгебраической сумме потенциалов,
создаваемых в этой точке каждым зарядом
в отдельности
(с учетом знаков потенциалов).
i
74

75.

Из механики известно, что если сила консервативна, то
работа этой силы равна убыли потенциальной энергии
тела, к которому эта сила приложена. Как показано выше,
электростатические силы консервативны, следовательно,
их работа равна убыли энергии перемещённого заряда.
A12 = - ∆Wпот =W1 –W2 , где
,
поэтому
Работа, совершаемая силами электростатического
поля при перемещении заряда, равна произведению
величины этого заряда на разность потенциалов в
начальной и конечной точках пути.
A12 = Wп1 – Wп2 = qφ1 – qφ2 = q(φ1 – φ2).
75

76.

76

77.

Как и потенциальная энергия, потенциал определяется
не однозначно, а с точностью до произвольной постоянной, зависящей от выбора нулевого уровня потенциала.
Нулевой уровень потенциала, (начало отчёта φ), может
быть выбран в бесконечности, на поверхности Земли и,
вообще говоря, где угодно. Это определяется удобством
расчетов.
• В Международной системе единиц (СИ) единицей
потенциала является вольт (В). 1 В = 1 Дж / 1 Кл.
• Работа в 1 Эв (внесистемная единица) - это работа,
совершаемая силами поля по перемещению заряда,
равного заряду электрона (q=- 1,6 • 10 -19 Кл), при
прохождении им разности потенциалов в 1 вольт
• ( φ = 1В ). 1Эв = 1,6 • 10 -19 Кл*1В= 1,6 • 10 -19 Дж
77

78. Таким образом: -- разность потенциалов – это работа электростати-ческих сил по перемещению единичного положитель-ного заряда из

Потенциал – величина алгебраическая, может быть
как положительным так и отрицательным
Таким образом:
-- разность потенциалов – это работа электростатических сил по перемещению единичного положительного заряда из одной точки в другую
-- потенциал – это работа электростатических
сил по перемещению единичного положительного заряда из данной точки в бесконечность
( где φ= 0 )

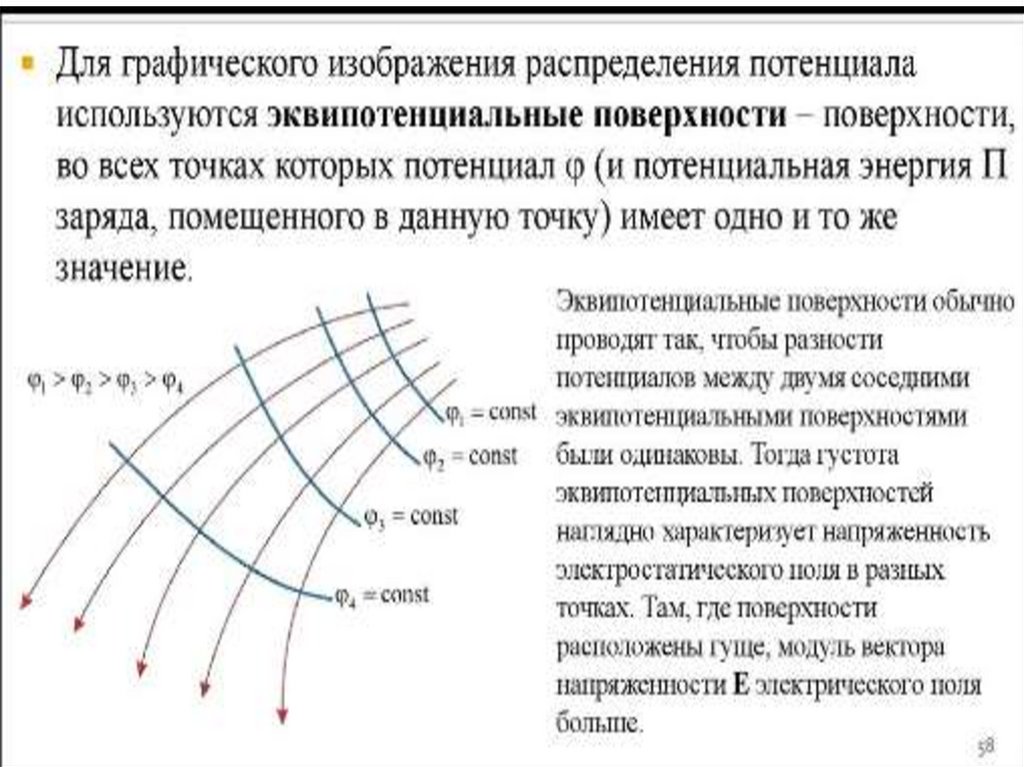
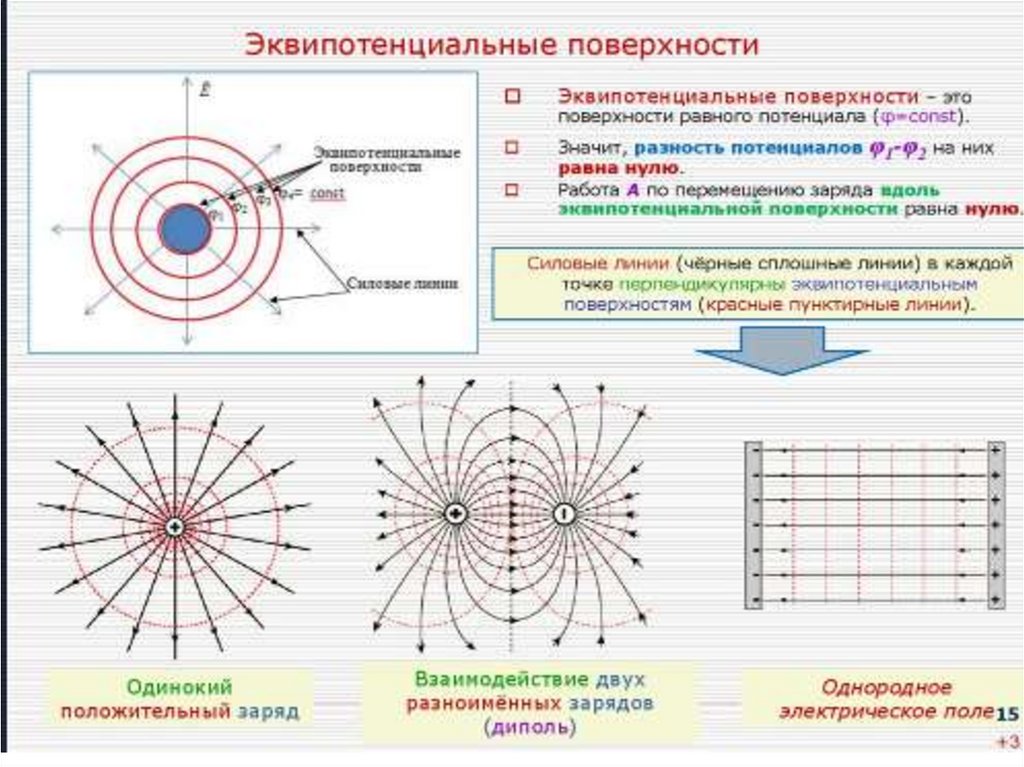
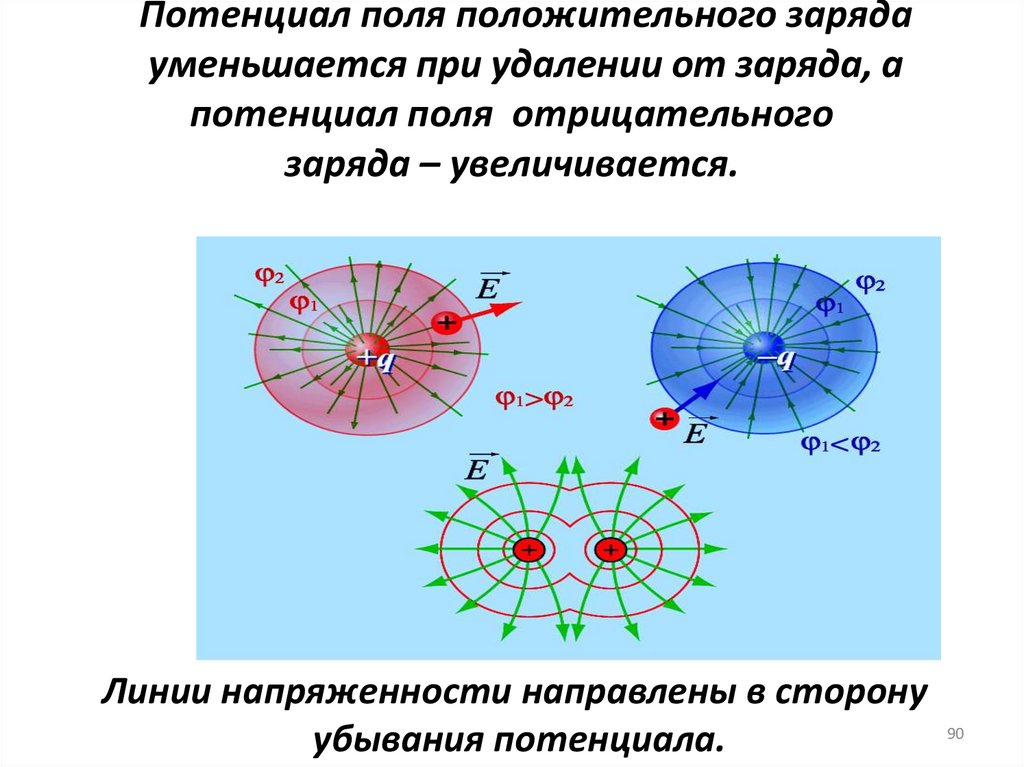
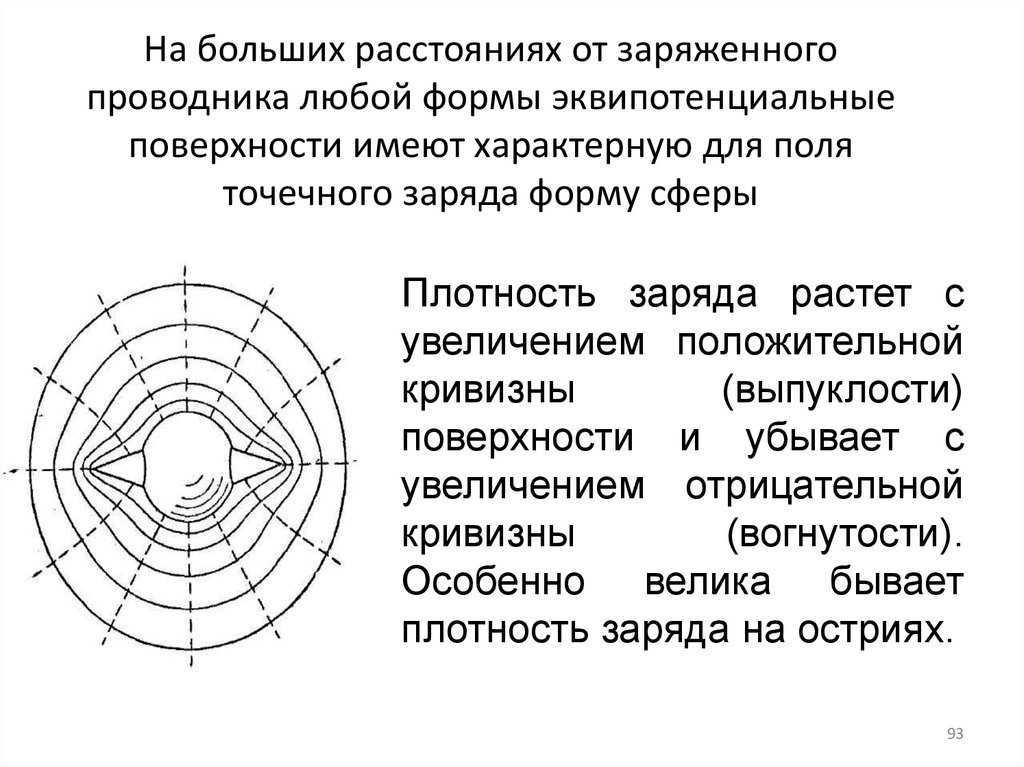
79. Эквипотенциальные поверхности

Потенциал φ поля точечного заряда q на
расстоянии r от него относительно бесконечно
удаленной точки вычисляется следующим
образом:
Для наглядного представления электрического
поля наряду с силовыми линиями используют
эквипотенциальные поверхности. Как следует
из названия, эквипотенциальная поверхность –
это такая поверхность, все точки которой имеют
одинаковый (равный) потенциал

80.

80

81.

81

82.

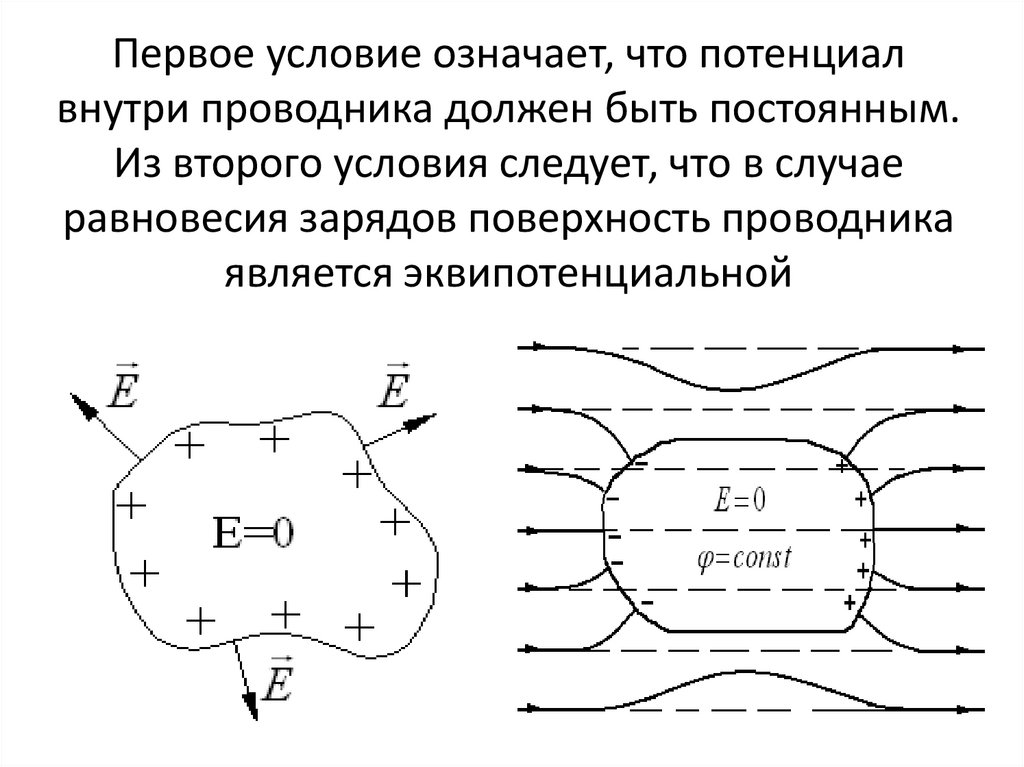
Свойства эквипотенциальных
поверхностей:
1. Линии напряженности электростатического поля
перпендикулярны эквипотенциальным поверхностям.
2.
Работа
по
перемещению
заряда
вдоль
эквипотенциальной поверхности равна нулю.
3. Эквипотенциальные поверхности не пересекаются ,
они замкнуты.
4. Эквипотенциальные поверхности строятся таким
образом, чтобы разность потенциалов между соседними
поверхностями
была
одинакова.
Густота
эквипотенциальных поверхностей пропорциональна
величине напряженности электростатического поля.
82

83. Работа электрического поля по перемещению электрического заряда вдоль эквипотенциальной поверхности равна A = q0(φ1 - φ2 ),

Работа электрического поля по перемещению
электрического заряда вдоль эквипотенциальной
поверхности равна A = q0(φ1 - φ2 ), т.к. поверхность
эквипотенциальная, то φ1 = φ2 , А=0
Тогда A= Eq0rcos α =0, следовательно cos α =0, где
угол α – угол между действующей электрической силой
F (F=Eq0) и перемещением( вдоль эквипотенциальной
поверхности).
Следовательно, линии напряженности электрического поля всегда нормальны к эквипотенциальным
поверхностям, т.к. если cos α =0, то α =90
83

84.

Эквипотенциальную поверхность можно провести
через любую точку поля. Следовательно, таких поверхностей может быть построено бесконечное множество.
Условились, однако, проводить их таким образом, чтобы
разность потенциалов для двух соседних эквипотенциальных поверхностей была бы всюду одна и та же. Тогда
по густоте эквипотенциальных поверхностей можно
судить о величине напряжённости электрического поля.
Чем гуще располагаются эквипотенциальные поверхности, тем быстрее изменяется потенциал при перемещении
вдоль нормали к эквипотенциальной поверхности.
Для однородного поля эквипотенциальные поверхности, очевидно, представляют собой систему равноотстоящих друг от друга плоскостей, перпендикулярных к
направлению вектора напряжённости электрического
84
поля Е.

85.

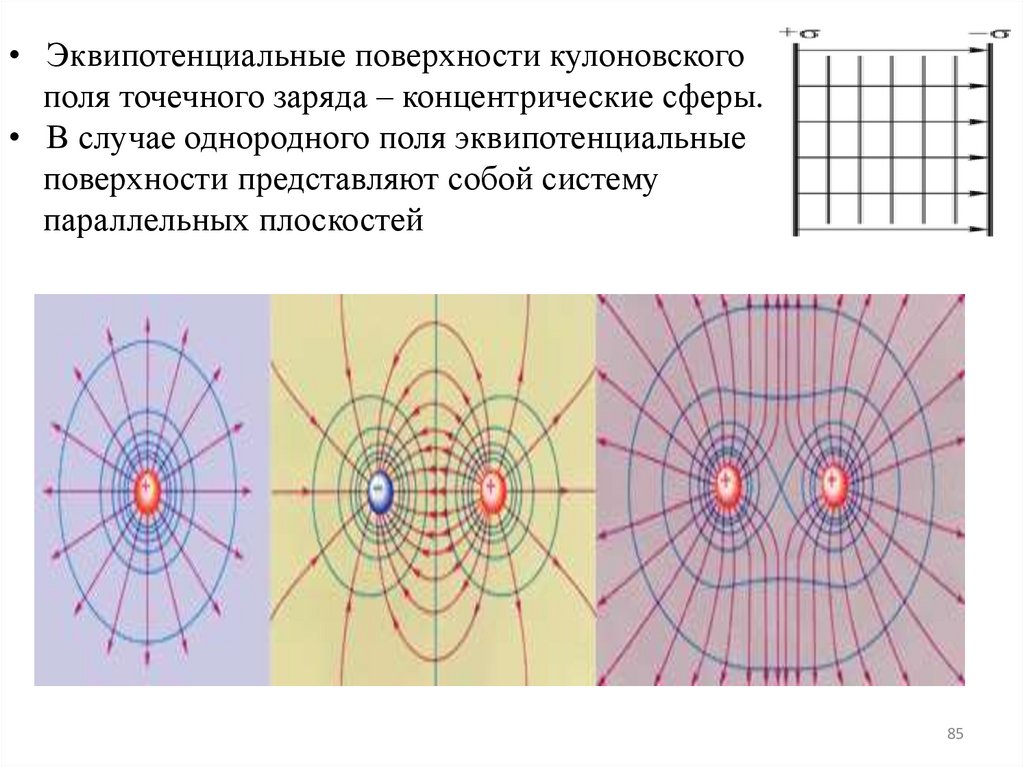
• Эквипотенциальные поверхности кулоновского
поля точечного заряда – концентрические сферы.
• В случае однородного поля эквипотенциальные
поверхности представляют собой систему
параллельных плоскостей
85

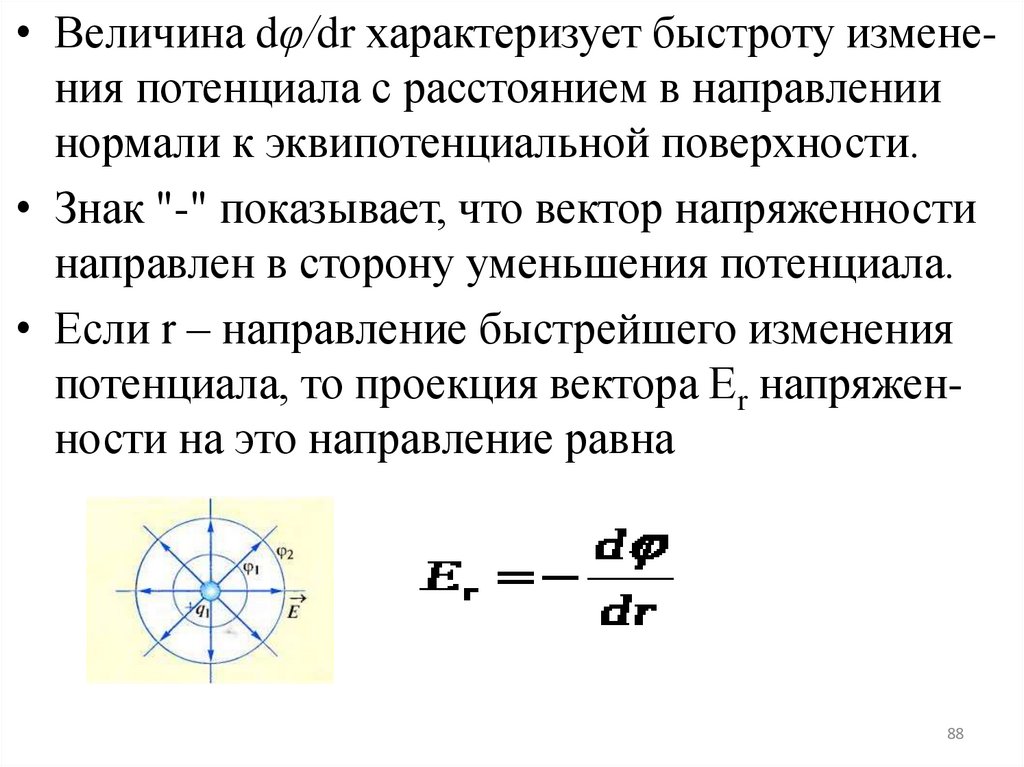
86. Связь между напряженностью поля и потенциалом

Электростатическое поле имеет две характеристики: силовую (напряжённость) и энергетическую (потенциал). Напряжённость и потенциал
– различные характеристики одной и той же
точки поля, следовательно, между ними должна
быть связь.
Рассмотрим в электростатическом поле две
бесконечно близкие
точки 1(а) и 2(б), где φ1 = φ,
φ2 = φ + dφ

87.

При перемещении заряда q из точки a эквипотенциальной поверхности (с потенциалом φ ) в точку b эквипотенциальной поверхности (с потенциалом(φ+dφ)) совершается работа dA = q(φ- (φ+ dφ ))= - qd