Динамика_5

1. Лекция 5

Теорема об изменении кинетического момента:
осевые моменты инерции тела; момент количества
движения (кинетический момент); теорема об
изменении момента количества движения точки,
кинетический момент вращающегося тела,
дифференциальное уравнение вращения твердого
тела .

2.

Осевые моменты инерции
При вращательном движении твердого тела мерой инерции
(сопротивления изменению движения) является момент
z
инерции относительно оси вращения.
1. Момент инерции материальной
h
точки относительно оси равен
m
произведению массы точки на
r
z
квадрат расстояния точки до оси:
O
y
I z mh m( x y )
2
2
2
h
x
x
y
2. Момент инерции твердого тела относительно оси равен
сумме произведений массы каждой точки на квадрат
расстояния этой точки до оси:
I z mk hk2 mk ( xk2 yk2 )
I z M 2z ρ - радиус инерции тела; М – масса тела

3.

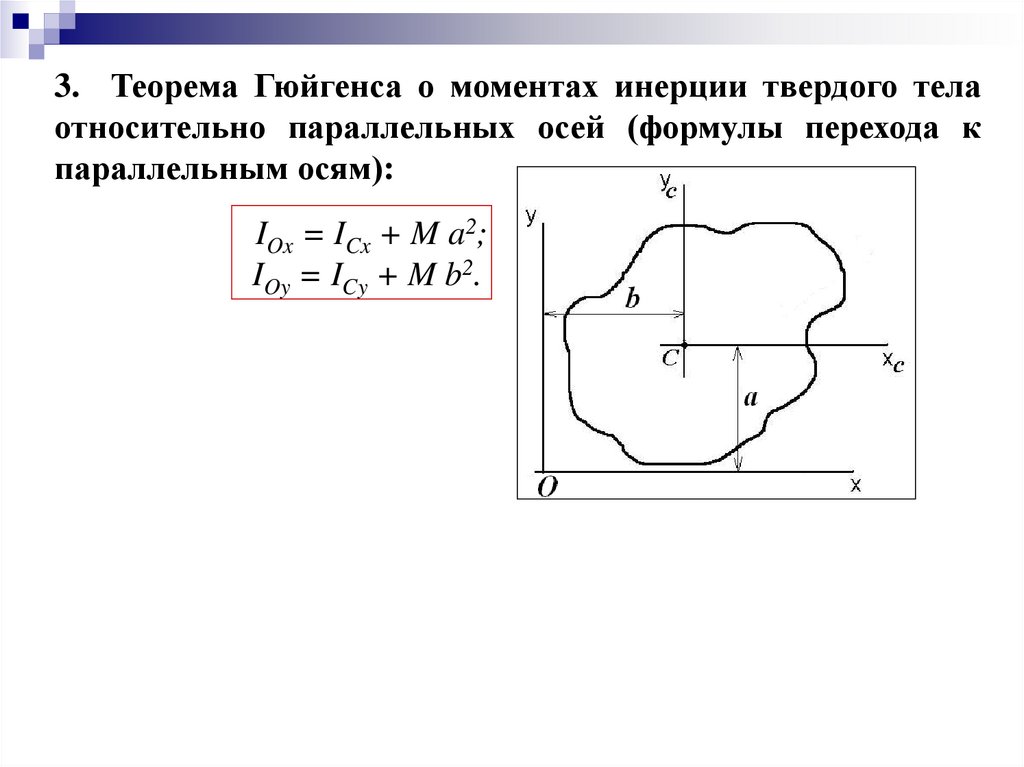
3. Теорема Гюйгенса о моментах инерции твердого тела
относительно параллельных осей (формулы перехода к
параллельным осям):
IOx = ICx + M a2;
IOy = ICy + M b2.

4.

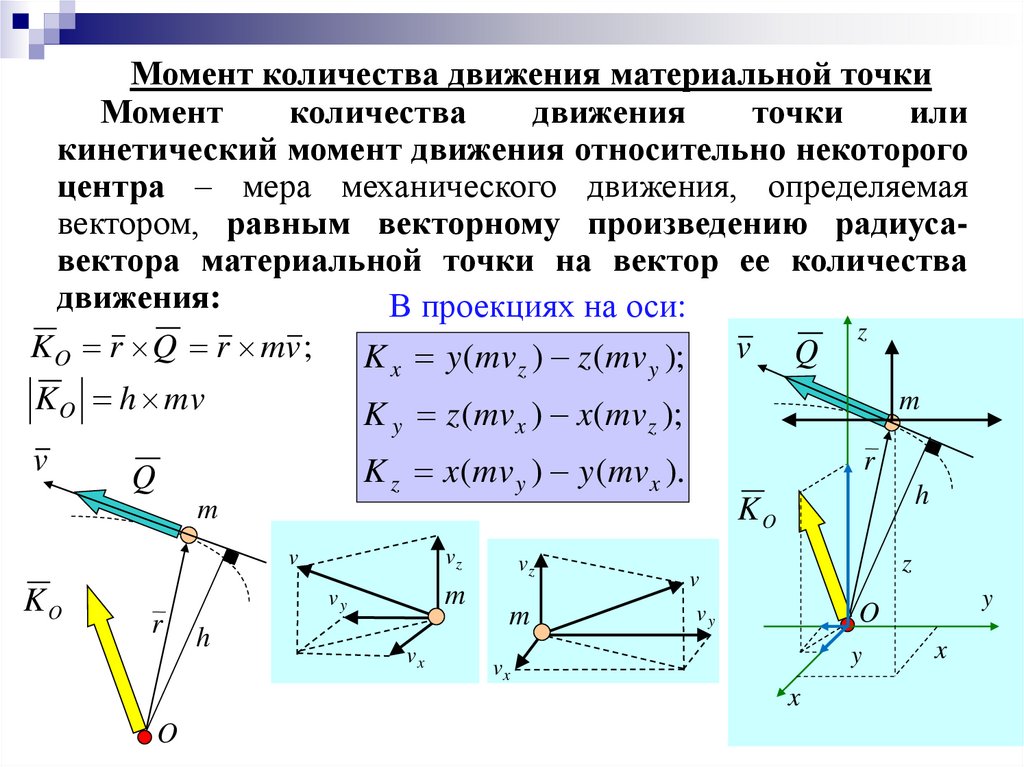
Момент количества движения материальной точки
Момент
количества
движения
точки
или
кинетический момент движения относительно некоторого
центра – мера механического движения, определяемая
вектором, равным векторному произведению радиусавектора материальной точки на вектор ее количества
движения:
В проекциях на оси:
z
K O r Q r mv ;
v
Q
K x y (mv z ) z (mv y );
K O h mv
m
K z (mv ) x(mv );
y
v
x
z
K z x(mv y ) y (mv x ).
Q
r
vz
v
KO
r
m
vy
h
h
KO
m
vx
vz
m
z
v
y
vx
x
O
y
O
vy
x

5.

Кинетический момент системы материальных
точек
относительно
некоторого
центра
–
геометрическая сумма моментов количеств движений
всех материальных точек относительно этого же центра:
KO
K r m v .
iO
i
i i
В проекциях на оси:
Kx
Kix ; K y Kiy ; K z Kiz .

6.

Теорема об изменении момента количества движения системы
Рассмотрим систему n материальных точек. Приложенные к
каждой точке силы разделим на внешние и внутренние и
заменим их на соответствующие равнодействующие Fke и Fki.
Запишем для каждой точки основное уравнение динамики:
Умножим векторно каждое из равенств
dvk
e
i
m
F
F
.
на радиус-вектор:
dvk
k
k
e
i k dt
rk mk
rk Fk rk Fk .
dt
Просуммируем уравнения r m dvk r F e r F i .
k
k
k
k
k
k
по всем точкам:
dt
d
После
(rk mk vk ) M Oe
M Oe
M Oi 0
преобразований
dt
dKO
получаем:
e
d
e
M
( rk mk vk ) M O
O
dt
dt
Производная вектора момента количества движения
системы относительно некоторого центра по времени равна
главному моменту внешних сил системы относительно этого
же центра. В проекциях на dK
dK y
dK
координатные оси:
x
dt
M xe ;
dt
M ye ;
z
dt
M ze .

7.

Следствия из теоремы об изменении момента
количества движения системы (законы сохранения):
1. Если в интервале времени [t1, t2] вектор главного момента
внешних сил системы относительно некоторого центра равен
нулю, MOe = 0, то вектор момента количества движения
системы относительно этого же центра постоянен, KO = const
– закон сохранения момента количества движения
системы.
2. Если в интервале времени [t1, t2] главный момент внешних
сил системы относительно оси X равен нулю, Mxe = 0, то
момент количества движения системы относительно оси X
постоянен, Kx = const.
Аналогичные утверждения справедливы для осей Y и Z.

8.

Кинетический момент вращающегося тела равен
произведению угловой скорости на момент инерции
z
относительно оси вращения.
ΔK zi hi Δmi vi hi Δmi z hi z hi2 Δmi ;
z
K z ΔK zi z h Δmi z I z .
vi
hi
Дифференциальное уравнение вращения
твердого тела относительно оси:
y
Δmi
Запишем теорему об изменении
x
кинетического момента твердого
тела,
вращающегося
вокруг dK z
e
M
z Мz
неподвижной оси:
dt
Кинетический момент вращающегося
K z z I z .
твердого тела равен:
Подставляем
кинетический d ( z I z )
d
d 2
M z Iz
I z 2 I z M z M вращ
момент в
dt
dt
dt
теорему:
2
i