первообразная

1. Первообразная

ПЕРВООБРАЗНАЯ
Преподаватель Бабакина Е.П.

2. Дифференцирование и интегрирование

ДИФФЕРЕНЦИРОВАНИЕ И
ИНТЕГРИРОВАНИЕ
Если проанализировать все математические действия, то большинству из них будет
соответствовать какое-то обратное:
сложение обратно вычитанию,
умножение — делению,
возведение в степень — извлечению арифметического корня.
С производной то же самое: мы можем продифференцировать функцию, а можем
произвести обратный процесс — интегрирование.
Дифференциация — операция взятия полной или частной производной функции.
Интегрирование — процесс поиска интеграла; восстановление функции по её
производной.

3.

Нахождение производной от функции обозначается знаком ′. Так, если
исходная функция — y, то её производная будет обозначаться y′.

4.

5. Правила дифференцирования

ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ

6.

7. Дифференциал

ДИФФЕРЕНЦИАЛ

8. Для понимания важности дифференциала в записи рассмотрим рисунок:

ДЛЯ ПОНИМАНИЯ ВАЖНОСТИ
ДИФФЕРЕНЦИАЛА В ЗАПИСИ
РАССМОТРИМ РИСУНОК:
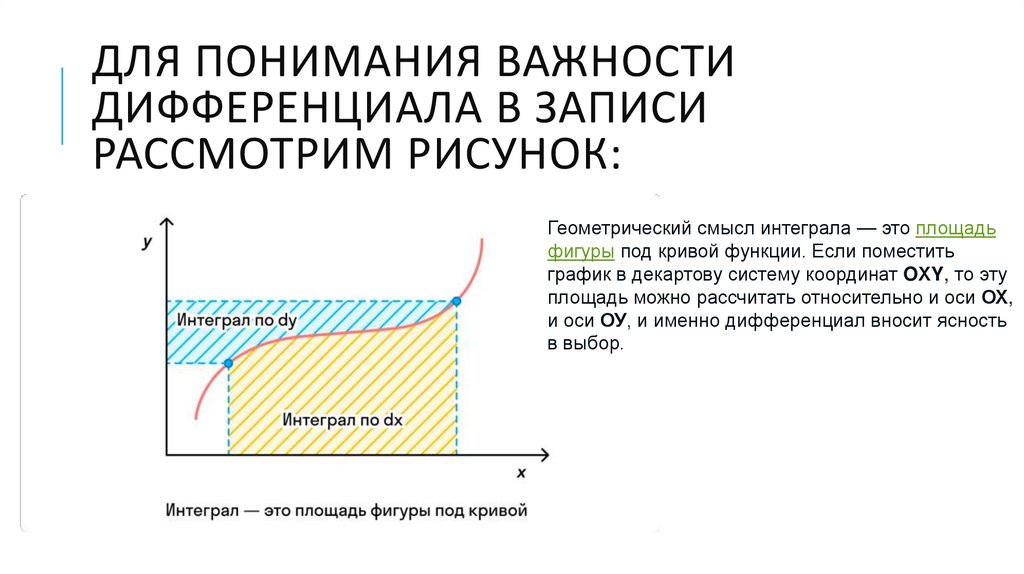
Геометрический смысл интеграла — это площадь
фигуры под кривой функции. Если поместить
график в декартову систему координат OХY, то эту
площадь можно рассчитать относительно и оси ОХ,
и оси ОУ, и именно дифференциал вносит ясность
в выбор.

9.

10. Константа

КОНСТАНТА

11. Правила нахождения первообразной

ПРАВИЛА НАХОЖДЕНИЯ
ПЕРВООБРАЗНОЙ
Нахождение первообразной функции технически связано с поиском неопределённого интеграла функции.
Неопределённый интеграл — это интеграл, для которого не задан промежуток интегрирования.

12.

Важный момент: если продифференцировать можно любую функцию, то найти
первообразную функции можно не всегда.
Об этом говорит достаточное условие интегрируемости: если на некотором
промежутке функция непрерывна, то она интегрируема на нём.

13.

14.

15.

Полезная информация о первообразной
Множество первообразных функции – это
неопределенный интеграл
Если F (x) – первообразная f(x), то множество
функций F (x) + C, где C – постоянная –
неопределенный интеграл
∫ f(x)dx = F (x) + C
Интегрирование применяли еще в античности
О том, что основы интегрирования применялись в
древности, говорит метод исчерпывания Евдокса в
4 в. до н.э. Но вместо интеграла использовалось
понятие квадратуры
Теория интегрирования сформулирована в 17 веке
Ньютон и Лейбниц сформировали понятие
интеграла и представили законченную
математическую теорию. На тот момент она была
еще «сырой» и окончательно сформировалась
только в 19-20 в.