Цифровой мир 2025 (Лебединская) final

1. Вероятностный прием MIMO-сигналов

15-ая школа-семинар «Инфокоммуникационные технологии в цифровом мире»
Вероятностный прием
MIMO-сигналов
Лебединская Анастасия Дмитриевна, СПбГЭТУ «ЛЭТИ»
Сергиенко Александр Борисович, СПбГЭТУ «ЛЭТИ»
2025

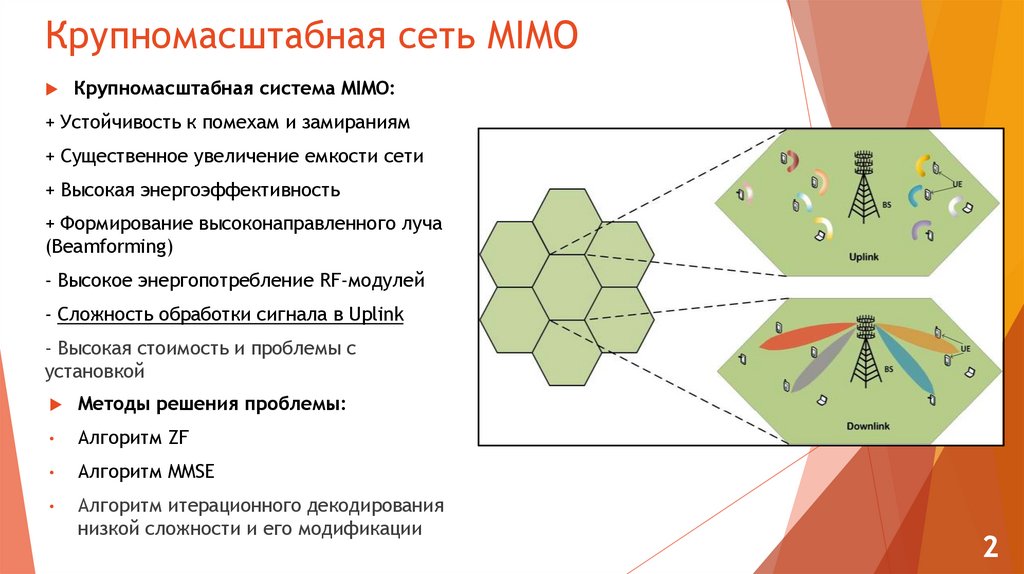
2. Крупномасштабная сеть MIMO

Крупномасштабная система MIMO:
+ Устойчивость к помехам и замираниям
+ Существенное увеличение емкости сети
+ Высокая энергоэффективность
+ Формирование высоконаправленного луча
(Beamforming)
- Высокое энергопотребление RF-модулей
- Сложность обработки сигнала в Uplink
- Высокая стоимость и проблемы с
установкой
Методы решения проблемы:
Алгоритм ZF
Алгоритм MMSE
Алгоритм итерационного декодирования
низкой сложности и его модификации
2

3. Алгоритм форсирования нуля (ZF)

В системе MIMO с N передающими и M приемными антеннами (где M ≥ N)
принятый сигнал можно записать как
y = Hs + n,
где H — матрица канала, s — передаваемый сигнал, n — аддитивный белый
гауссовский шум с дисперсией σ².
Ключевая идея ZF: найти такую обратную матрицу W к матрице канала H,
которая при умножении на принятый сигнал y устранит межпотоковые
помехи, оставив только полезный сигнал и усиленный шум.
Математически: Матрица обработки ZF вычисляется как псевдообратная
матрица Мура-Пенроуза: W = (HᴴH)⁻¹Hᴴ.
Оценка переданного сигнала: s’ = W * y = s + (HᴴH)⁻¹Hᴴn.
Процесс: Применяя W к y, мы «инвертируем» эффект канала. Идеальная
диагонализация (W * H = I) приводит к тому, что каждый оцененный поток
данных зависит только от своего переданного символа, но шумовая
составляющая n умножается на W.
3

4. Алгоритм минимизации среднеквадратической ошибки (MMSE)

В системе MIMO с N передающими и M приемными антеннами (где M ≥ N)
принятый сигнал можно записать как
y = Hs + n,
где H — матрица канала, s — передаваемый сигнал, n — аддитивный белый
гауссовский шум с дисперсией σ².
Ключевая идея MMSE: найти такую матрицу обработки W, которая минимизирует
математическое ожидание среднеквадратичной ошибки между оцененным
переданным сигналом s’ и истинным s.
Математически: Оптимальная матрица MMSE находится по формуле:
W = (HᴴH + σ²I)⁻¹Hᴴ
где σ² — мощность шума, I — единичная матрица. Оценка сигнала: s’ = W * y.
Интерпретация: Добавление слагаемого σ²I перед обращением действует
как регуляризация, которое стабилизирует обращение матрицы, предотвращая
"взрыв" коэффициентов при плохой обусловленности H (когда подканалы сильно
коррелированы).
4

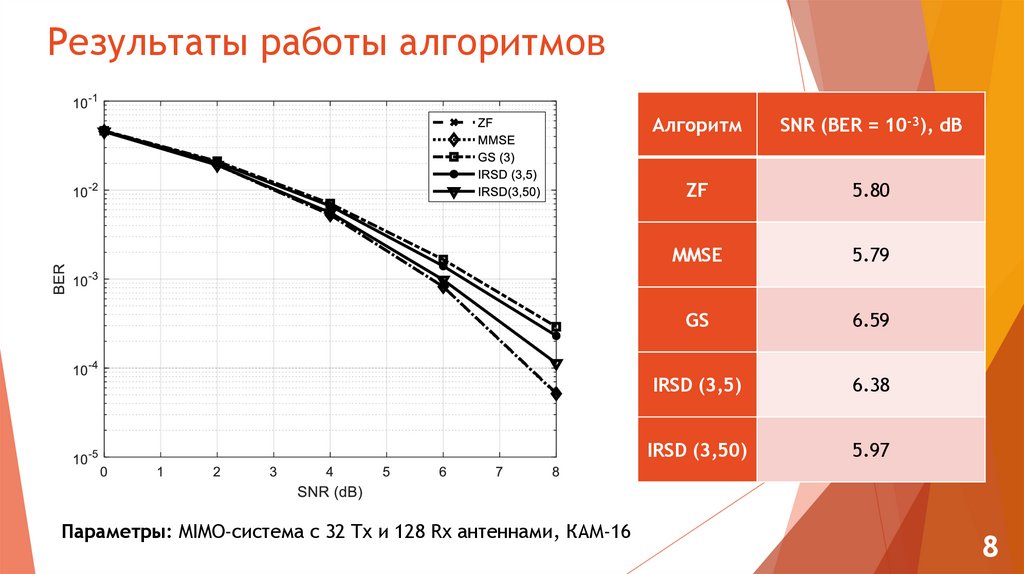
5. Алгоритм итерационного декодирования низкой сложности

Шаги алгоритма Гаусса-Зейделя (GS):
1.
Формирование эквивалентной линейной системы:
A = HᵀH ∈ ℝ(m×m) (ZF фильтр)
b = Hᵀc ∈ ℝm
2.
Система уравнений: A·s = b, где s ∈