Similar presentations:
9ffa9fc7fdff4cc29e66645c4571af70
1.
Некоторые свойствапрямоугольных треугольников.
Свойство медианы
прямоугольного треугольника.
2.
ПОВТОРИМ!• Остроугольный треугольник – треугольник, у которого все углы острые.
• Тупоугольный треугольник – треугольник, у которого два угла острые, а
третий – тупой.
• Прямоугольный треугольник – треугольник, у которого два угла острые,
а один – прямой, т.е. равный 90°.
3.
Элемент ы прямоугольного треугольника• Сторона прямоугольного треугольника,
лежащая
напротив
прямого
угла,
называется гипотенузой, а две другие
стороны – катетами.
• Обратите внимание, на рисунке изображён
АВС с прямым углом С, в прямоугольном
треугольнике гипотенуза всегда является
самой большой стороной.
4.
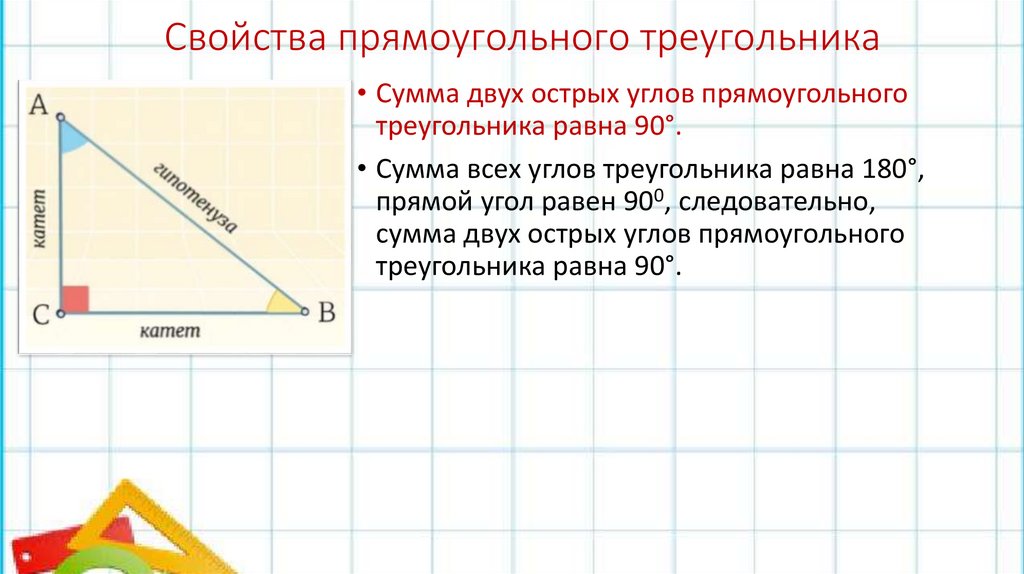
Свойства прямоугольного треугольника• Сумма двух острых углов прямоугольного
треугольника равна 90°.
• Сумма всех углов треугольника равна 180°,
прямой угол равен 900, следовательно,
сумма двух острых углов прямоугольного
треугольника равна 90°.
5.
Свойства прямоугольного треугольника• Катет прямоугольного треугольника, лежащий
напротив угла 300, равен половине гипотенузы.
• Рассмотрим прямоугольный АВС, в котором ∠А –
прямой, ∠В = 30° и, значит, ∠С = 60°.
• Докажем, что АC = ½ BC
• Достроим к АВС равный ему ABD так, как у нас
показано на рисунке. Получим ВСD, в котором ∠В
= ∠D = 60°, поэтому DC = BC (по признаку
равнобедренного треугольника). Но АС = ½
DC. Следовательно, АС = ½BC, что и требовалось
доказать.
6.
Свойства прямоугольного треугольника• Если катет прямоугольного треугольника
равен половине гипотенузы, то угол,
лежащий против этого катета, равен 30°.
• Рассмотрим прямоугольный АВС, у
которого катет АС равен половине
гипотенузы ВС. Докажем, что ∠АВС = 30°.
• Достроим к АВС равный ему ABD так,
как у нас показано на рисунке. Получим
равносторонний
BCD.
Углы
равностороннего треугольника равны
друг другу (т.к. сумма углов треугольника
равна 180°, а в равностороннем
треугольнике
все
углы
равны,
следовательно, 180° : 3= 60° – каждый
угол равностороннего треугольника). В
частности, ∠DВС = 60°. Но ∠DВС= 2∠АВС.
Следовательно, ∠АВС = 30°, что и
требовалось доказать.
7.
Свойства прямоугольного треугольникаВ прямоугольном треугольнике медиана, проведённая из вершины
прямого угла к гипотенузе, равна половине гипотенузы.
8.
Задача 1Установите соответствие между градусными мерами так, чтобы они
составляли пары острых углов для одного прямоугольного треугольника.
9.
Задача 2Чему равен второй острый угол в
прямоугольном треугольнике, если первый
равен 39°?
Дано: АВС – прямоугольный, С = 90 ,
А=39
Найти: В
Решение
В = 90 - А= 90 - 39 = 51
Ответ: 51
10.
Задача 3Вставьте пропущенные элементы таблицы. Укажите, существуют ли такие
пары катет и гипотенуза, если указанный катет лежит напротив угла 30°.
Катет
Гипотенуза
Да / Нет
70
129
Нет
61
122
Да
13
27
49
98
Нет
Да
11.
Задача 4В треугольнике ABC ∠C = 90°, АВ =
36 см, СВ = 18 см. Чему равен В?
Дано: АВС – прямоугольный,
С = 90 , АВ = 36 см, СВ = 18 см.
Найти: ∠В
Решение
Так как АВ = 36 см, СВ = 18 см, то
А = 30 .
Тогда ∠В = 90 -∠A = 90 - 30 = 60
Ответ: 60
12.
Задача 513.
Задача 6В прямоугольном АFС угол между биссектрисой СК и
высотой СН, проведёнными из вершины прямого угла С,
равен 15°. Сторона АF = 48 см. Найдите сторону АС, если
известно, что точка К лежит между F и Н.
Дано: АFС – прямоугольный, С = 90 , НСК = 15 , СН –
высота, СК – биссектриса, АF = 48 см.
Найти: АС
Решение
1. Из НСК: НСК = 15 , СН – высота, значит, СНК = 90 .
СКН = 180 - 90 - 15 = 75 .
2. Так как СК – биссектриса, то АСК = КСF = 90 :2 = 45
3. СКF = 180 - СКA = 180 -75 = 105 - как смежные
4. Из FСК: СFК = 180 - СКF - KСF = 180 - 105 - 45 = 30 .
АС = АF:2 = 48:2 = 24 (см)
Ответ: 24 см
14.
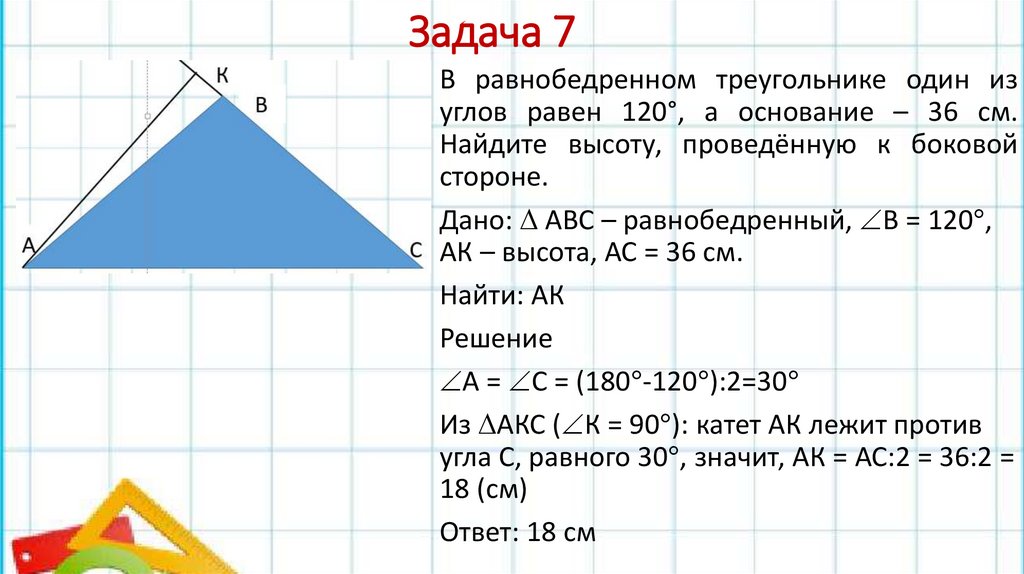
Задача 7В равнобедренном треугольнике один из
углов равен 120°, а основание – 36 см.
Найдите высоту, проведённую к боковой
стороне.
Дано: АВС – равнобедренный, В = 120 ,
АК – высота, АС = 36 см.
Найти: АК
Решение
А = С = (180 -120 ):2=30
Из АКС ( К = 90 ): катет АК лежит против
угла С, равного 30 , значит, АК = АС:2 = 36:2 =
18 (см)
Ответ: 18 см
15.
Задача 8Выберите правильный ответ
Дан треугольник АВС, ∠С = 90°, СН – высота, ∠А = 57°.
Найдите ∠1, ∠2, ∠3.













 mathematics
mathematics








