5_Инвестиционный_анализ,_Лекция_ppsx (2)

1. Инвестиционный анализ

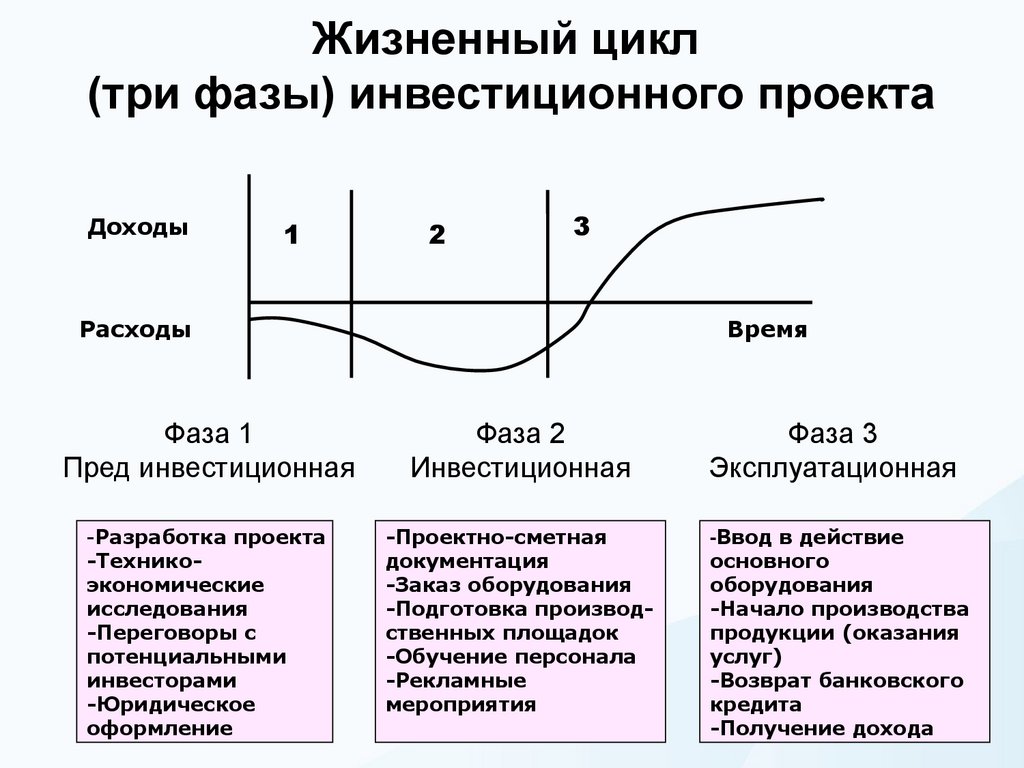
1

2. Жизненный цикл (три фазы) инвестиционного проекта

Доходы
1
2
3
Расходы
Время
Фаза 1
Пред инвестиционная
Фаза 2
Инвестиционная
Фаза 3
Эксплуатационная
-Разработка проекта
-Проектно-сметная
документация
-Заказ оборудования
-Подготовка производственных площадок
-Обучение персонала
-Рекламные
мероприятия
-Ввод в действие
основного
оборудования
-Начало производства
продукции (оказания
услуг)
-Возврат банковского
кредита
-Получение дохода 2
-Техникоэкономические
исследования
-Переговоры с
потенциальными
инвесторами
-Юридическое
оформление

3. Показатели эффективности проектов

• NPV (Net Present Value ) - чистая приведенная (текущая,
дисконтированная, современная) стоимость
• IRR (Internal Rate of Return) - внутренняя норма доходности
• ROI (Return on investment) – рентабельность инвестиций
Срок окупаемости:
• PP (Pay-back Period ) - простой срок окупаемости (без
дисконтирования);
• DPP (Discounted Pay-back Period) - дисконтированный срок
окупаемости.
3

4. Эффективность инвестиционного проекта

• Принятие инвестиционных решений по финансированию развития
бизнес-проектов основываются на оценки эффективности
предполагаемых капиталовложений.
• В основе такой оценки лежат:
- для одного бизнес-проекта - расчет и сравнение объема
предполагаемых инвестиций и будущих доходов (денежных
поступлений);
- для различных бизнес-проектов - сравнение эффективности
инвестиций.
• При этом в качестве альтернативы вложений средств в
инвестиционные проекты выступают:
- финансовые вложения в другие производственные объекты;
- помещение финансовых средств в банк под проценты или
обращение их в ценные бумаги.

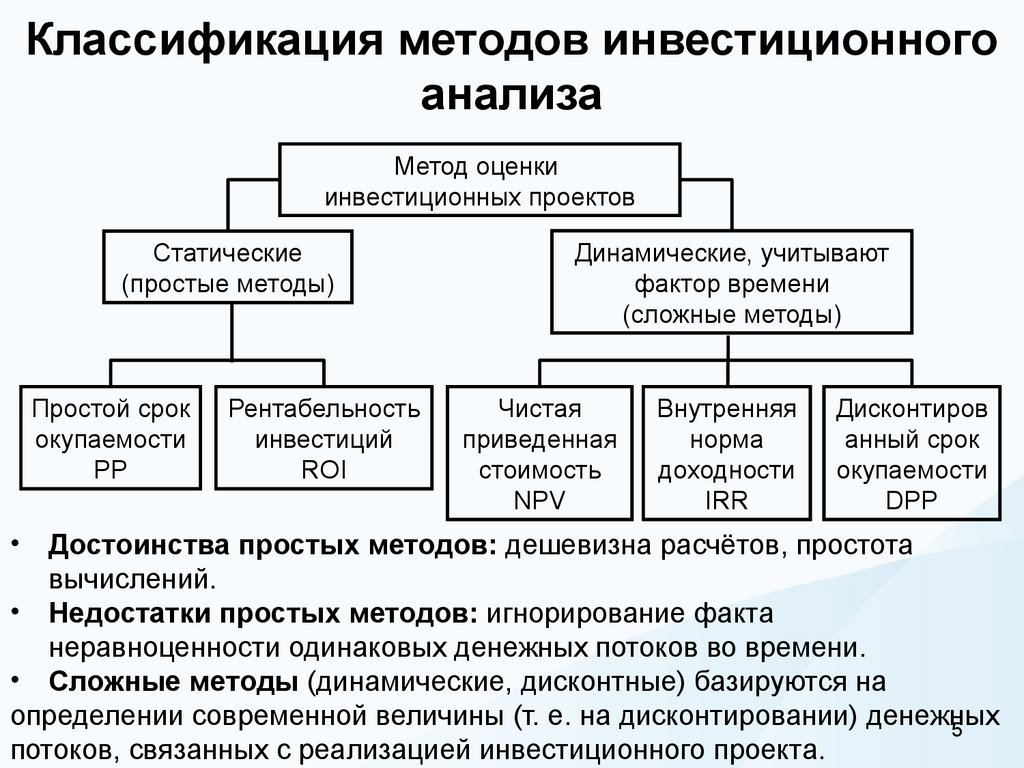
5. Классификация методов инвестиционного анализа

Метод оценки
инвестиционных проектов
Статические
(простые методы)
Простой срок
окупаемости
PP
Рентабельность
инвестиций
ROI
Динамические, учитывают
фактор времени
(сложные методы)
Чистая
приведенная
стоимость
NPV
Внутренняя
норма
доходности
IRR
Дисконтиров
анный срок
окупаемости
DPP
• Достоинства простых методов: дешевизна расчётов, простота
вычислений.
• Недостатки простых методов: игнорирование факта
неравноценности одинаковых денежных потоков во времени.
• Сложные методы (динамические, дисконтные) базируются на
определении современной величины (т. е. на дисконтировании) денежных
5
потоков, связанных с реализацией инвестиционного проекта.

6. Простой срок окупаемости инвестиционного проекта (РР)

Срок окупаемости — это количество лет, в течение которых инвестиция
в проект возвратится инвестору в виде чистого дохода.
Алгоритм расчета простого срока окупаемости (РР) зависит от
равномерности распределения планируемых доходов. Здесь
возможны два варианта:
1-й вариант — доход распределяется по годам равномерно. В этом
случае срок окупаемости рассчитывается делением единовременных
затрат на величину годового дохода:
где:
• PP – Простой срок окупаемости инвестиций
• I0 – Инвестиции
• CFt – Денежный поток

7. Простой срок окупаемости инвестиционного проекта (РР)

• 2-й вариант предусматривает, что доход от инвестиции по годам
распределяется неравномерно. В этом случае простой срок
окупаемости рассчитывается прямым подсчетом числа лeт, в
течение которых инвестиция будет погашена кумулятивным
доходом:
где:
PP – Простой срок окупаемости инвестиций
I0
– Инвестиции
CFt – Денежный поток
n
- число лeт, в течение которых инвестиция будет
погашена

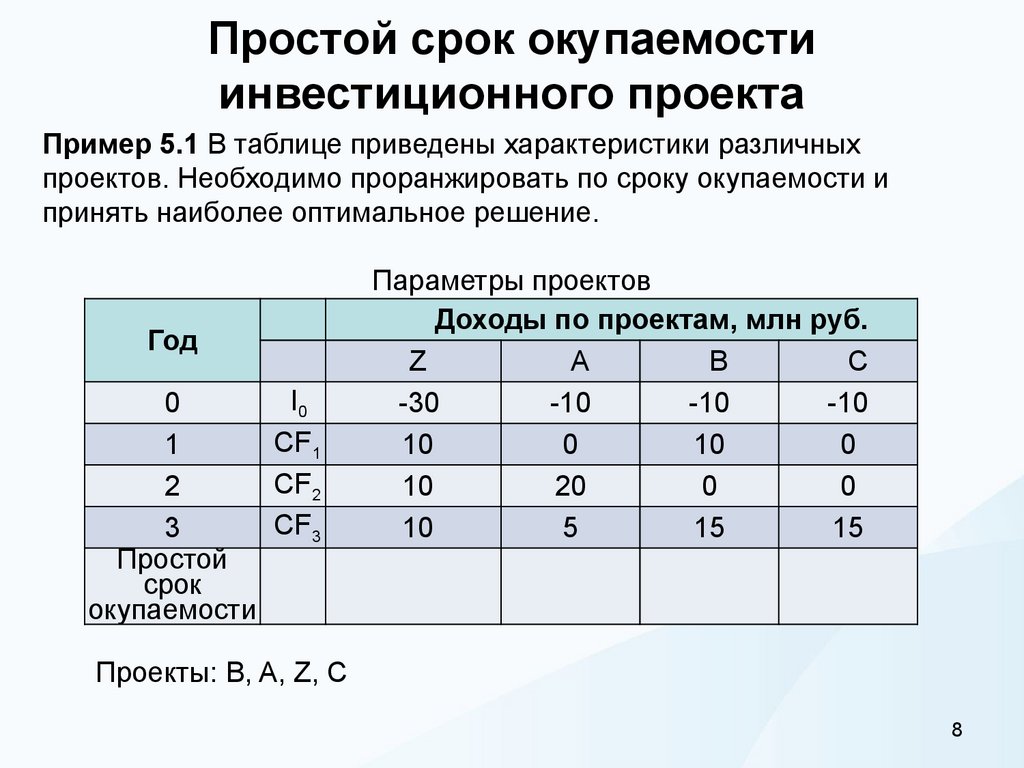
8. Простой срок окупаемости инвестиционного проекта

Пример 5.1 В таблице приведены характеристики различных
проектов. Необходимо проранжировать по сроку окупаемости и
принять наиболее оптимальное решение.
Год
I0
0
CF1
1
CF2
2
CF3
3
Простой
срок
окупаемости
Параметры проектов
Доходы по проектам, млн руб.
Z
А
В
С
-30
-10
-10
-10
10
0
10
0
10
20
0
0
10
5
15
15
Проекты: B, A, Z, C
8

9. 1) Концепция денежного потока

• Концепция денежного потока означает, что любую финансовую
операцию можно представить как некоторый денежный поток (cash
flow), т. е. множество распределенных во времени выплат (оттоков)
и поступлений (притоков).
• В качест­ве элемента денежного потока могут выступать денежные
поступле­ния, доход, расход, прибыль, платеж и др.
• В подавляющем большинст­ве случаев речь идет об ожидаемых
денежных потоках.
9

10. Классификация денежного потока

• Положительный денежный поток – все поступления (приход)
денежных средств.
• Отрицательный денежный поток – все выплаты (расход).
• Чистый денежный поток – это сумма положительного и
отрицательного денежного потока.
10

11. 2) Концепция временной ценности

• Концепция временной ценности состоит в том, что денежная
едини­ца, имеющаяся сегодня, и денежная единица, ожидаемая к
получению через какое-то время, неравноценны.
• Неравноценность определя­ется действием трех основных причин:
1) инфляцией,
2) риском неполуче­ния ожидаемой суммы и
3) оборачиваемостью.
1) В силу инфляции происходит обесценение денег, т. е. денежная
единица, получаемая позднее, имеет меньшую по­купательную
способность.
2) В экономике практически не бы­вает безрисковых ситуаций,
всегда существует вероятность того, что по каким-либо причинам
ожидаемая к получению сумма не будет получена.
3) По сравнению с денежной суммой, которая, возмож­но, будет
получена в будущем, та же самая сумма, имеющаяся в нали­чии в
данный момент времени, может быть немедленно пущена в обо­рот и
тем самым принесет дополнительный доход.

12. Временная ценность денежных ресурсов

• Денежные ресурсы, участвующие в типовой финансовой опера­ции,
имеют временную ценность, смысл которой следующий: одна
денежная единица, имеющаяся в распо­ряжении инвестора в
данный момент времени, более предпочтитель­на, чем та же
самая денежная единица, но ожидаемая к получению в
будущем.
• В основе финансовых вычислений лежат простейшие задачи,
связанные с начислением процентов и с потоками денежных
средств.
12

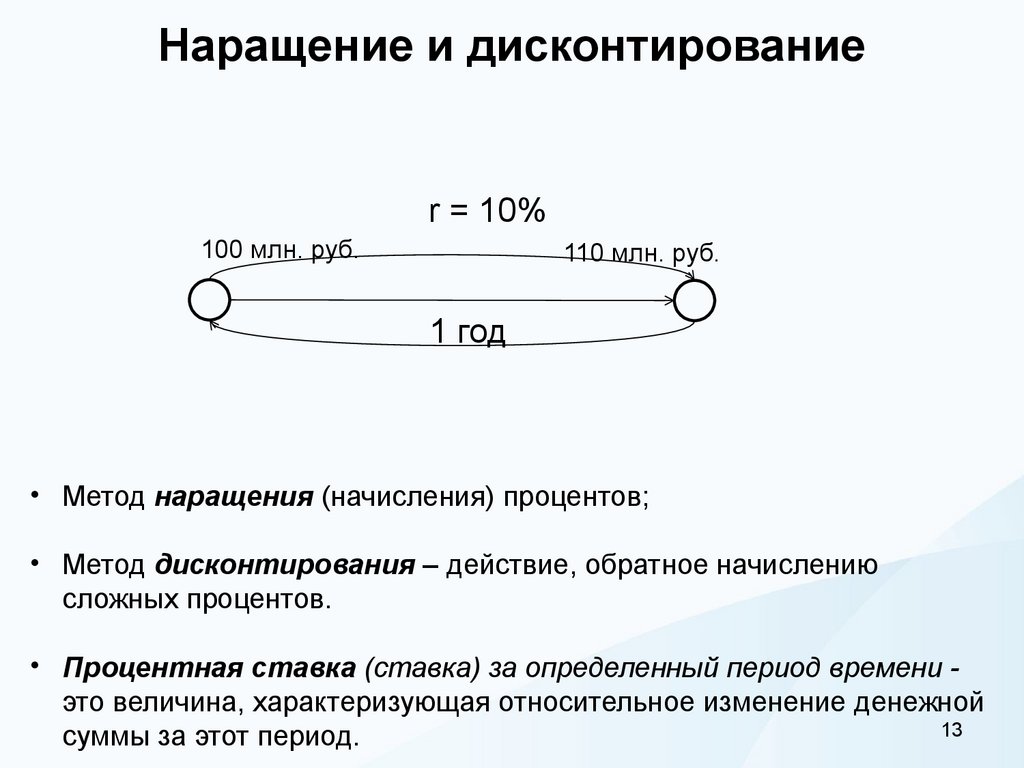
13. Наращение и дисконтирование

r = 10%
100 млн. руб.
110 млн. руб.
1 год
• Метод наращения (начисления) процентов;
• Метод дисконтирования – действие, обратное начислению
сложных процентов.
• Процентная ставка (ставка) за определенный период времени это величина, характеризующая относительное изменение денежной
13
суммы за этот период.

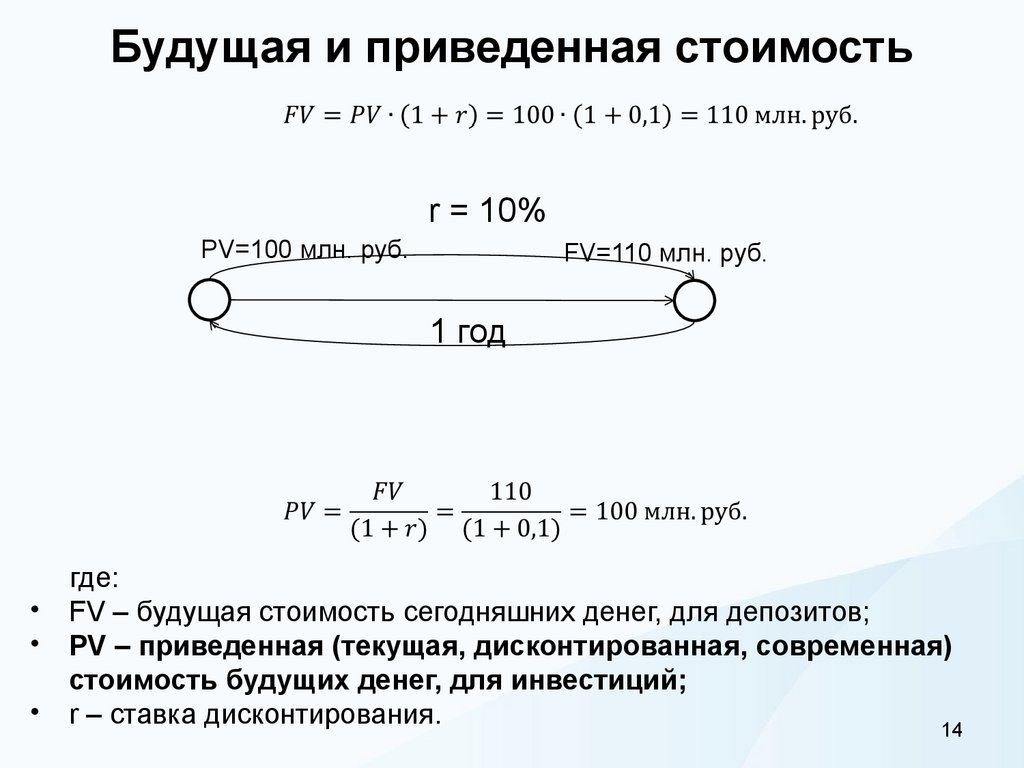
14. Будущая и приведенная стоимость

r = 10%
PV=100 млн. руб.
FV=110 млн. руб.
1 год
где:
• FV – будущая стоимость сегодняшних денег, для депозитов;
• PV – приведенная (текущая, дисконтированная, современная)
стоимость будущих денег, для инвестиций;
• r – ставка дисконтирования.
14

15. Наращение

• В зависимости от того, какая из указанных сумм дана и какую
нужно найти, выделяют два направления финансовых расчетов:
наращение и дисконтирование.
• Наращение — определение величины итоговой стоимости по
заданной текущей стоимости.
• Коэффициент наращения - отношение итоговой стоимости FV к
текущей стоимости PV.
• Коэффициент наращения характеризует темп роста денежных
средств за опре­деленный период.
15

16. Схемы начисления процентов

Известны две основные схемы начисления процентов:
• Схема простых процентов предполагает неизменность базы, с
которой проис­ходит начисление.
• Схема сложных процентов предполагает их капита­лизацию, т. е.
база, с которой происходит начисление, постоянно воз­растает на
величину начисленных ранее процентов.
• Очевидно, что более частое начисление сложных процентов
обеспечивает более быс­трый рост наращиваемой суммы.
16

17. Дисконтирование

• Дисконтирование — определение текущей стоимости по
ожидаемой сумме в будущем.
• Термин дисконтирование используется также для определения
значения любой стоимостной величины на более ранний момент
времени.
• Коэффициент дисконтирования - отношение текущей стоимости
(PV) к ожидаемой сумме в будущем (FV).
• Коэффициент дисконтирования характеризует уровень снижения
денежных средств при переходе от конца к началу финансовой
операции.
17

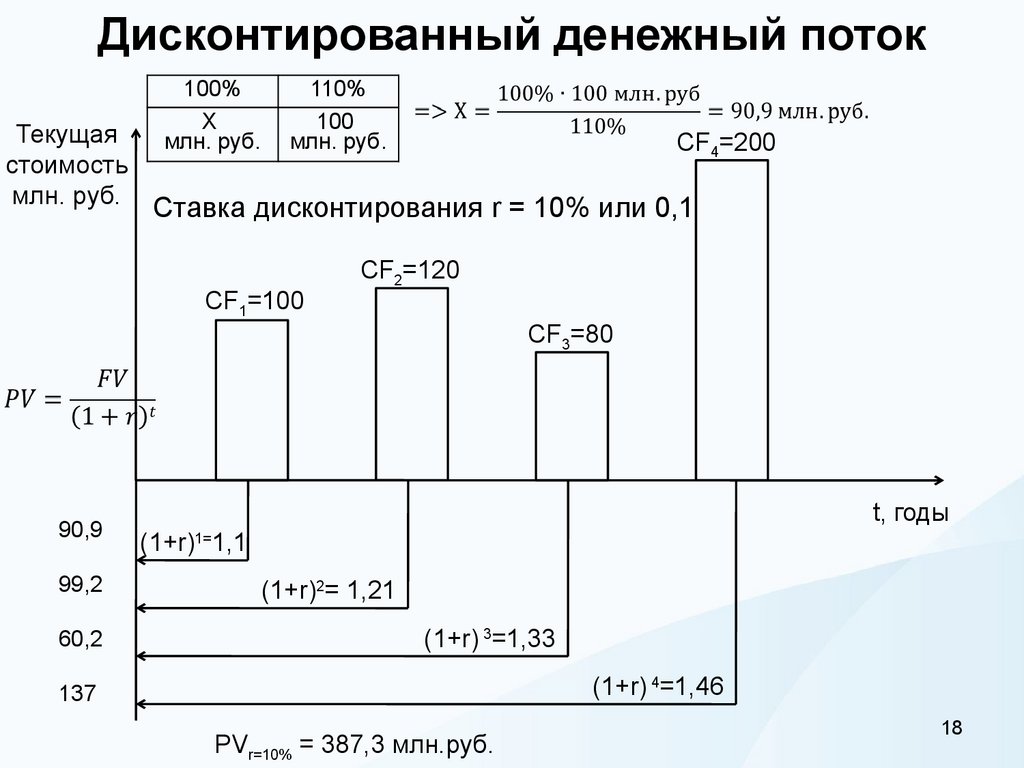
18. Дисконтированный денежный поток

Текущая
стоимость
млн. руб.
100%
Х
млн. руб.
110%
100
млн. руб.
CF4=200
Ставка дисконтирования r = 10% или 0,1
CF1=100
CF2=120
CF3=80
90,9
99,2
60,2
t, годы
(1+r)1=1,1
(1+r)2= 1,21
(1+r) 3=1,33
(1+r) 4=1,46
137
PVr=10% = 387,3 млн.руб.
18

19.

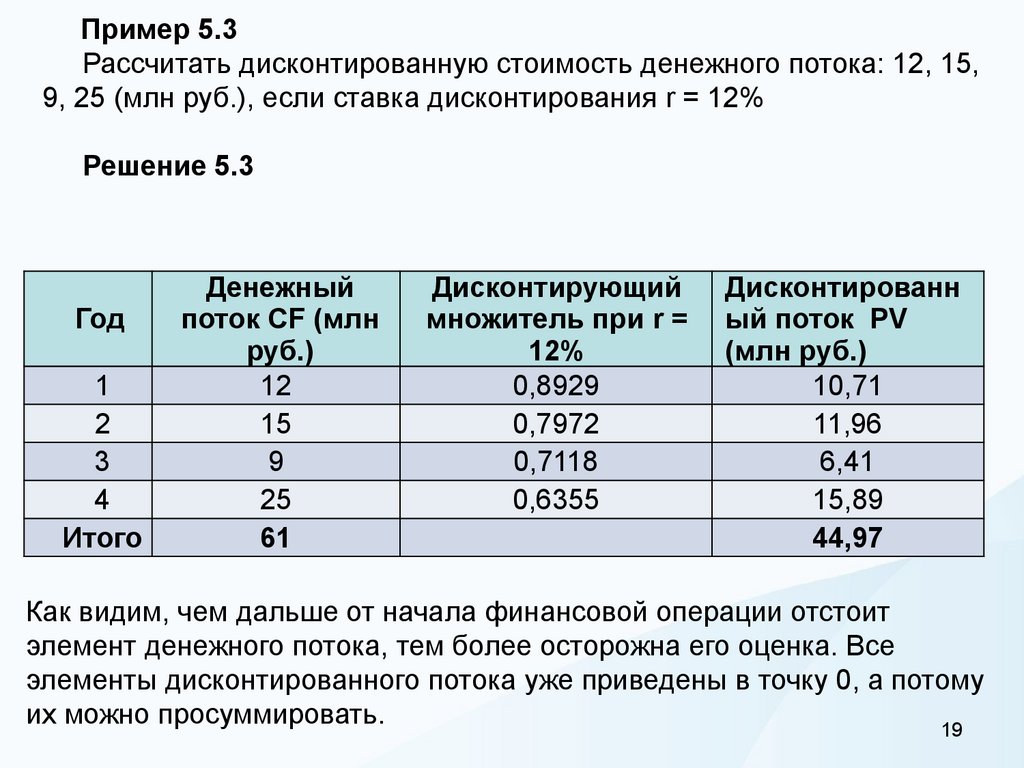
Пример 5.3
Рассчитать дисконтированную стоимость денежного потока: 12, 15,
9, 25 (млн руб.), если ставка дисконтирования r = 12%
Решение 5.3
Год
1
2
3
4
Итого
Денежный
поток CF (млн
руб.)
12
15
9
25
61
Дисконтирующий
множитель при r =
12%
0,8929
0,7972
0,7118
0,6355
Дисконтированн
ый поток PV
(млн руб.)
10,71
11,96
6,41
15,89
44,97
Как видим, чем дальше от начала финансовой операции отстоит
элемент денежного потока, тем более осторожна его оценка. Все
элементы дисконтированного потока уже приведены в точку 0, а потому
их можно просуммировать.
19

20. Метод чистой приведенной стоимости

• Основная идея чистой приведенной стоимости заключается в том,
чтобы найти разницу между инвестиционными затратами и
будущими доходами бизнес-проекта, выраженную в
скорректированной во времени (как правило, к началу реализации)
денежной величине.
• При заданной норме дисконта можно определить современную
величину всех оттоков и притоков денежных средств в течение
экономической жизни бизнес-проекта, а также сопоставить их друг с
другом. Результатом такого сопоставления будет положительная или
отрицательная величина (чистый приток или чистый отток денежных
средств), которая показывает, удовлетворяет или нет проект принятой
норме дисконта.
CF
-100 000
8 000 8 000 8 000 8 000 8 000 8 000 8 000 50 000, r=10%
1
2
3
4
5
6
7
8 годы
20

21. Чистая приведенная стоимость NPV

21

22. Чистая приведенная стоимость NPV

• При NPV > 0 проект возместит первоначальные затраты I0, обеспечит
получение прибыли согласно заданному дисконту r, а также ее
некоторый резерв, равный NPV.
• При NPV < 0 проект убыточен.
• При NPV = 0 проект только окупает произведенные затраты, но не
приносит дохода.
Общее правило NPV: если NPV > 0, то проект принимается, иначе
его следует отклонить.
22

23.

Пример 5.4
В целях увеличения объема продаж компания собирается вложить
средства в создание цеха деревообработки.
Совокупные расходы составят 100 000 тыс. руб.
Ожидается, что создание такой системы обеспечит получение, на
протяжении первых пяти лет чистых доходов в размере:
27 000,
31 000,
35 000,
39 000 и
44 000 тыс. руб. соответственно.
Принятая норма дисконта равна 8%.
Необходимо определить экономическою эффективность
предлагаемого проекта.
23

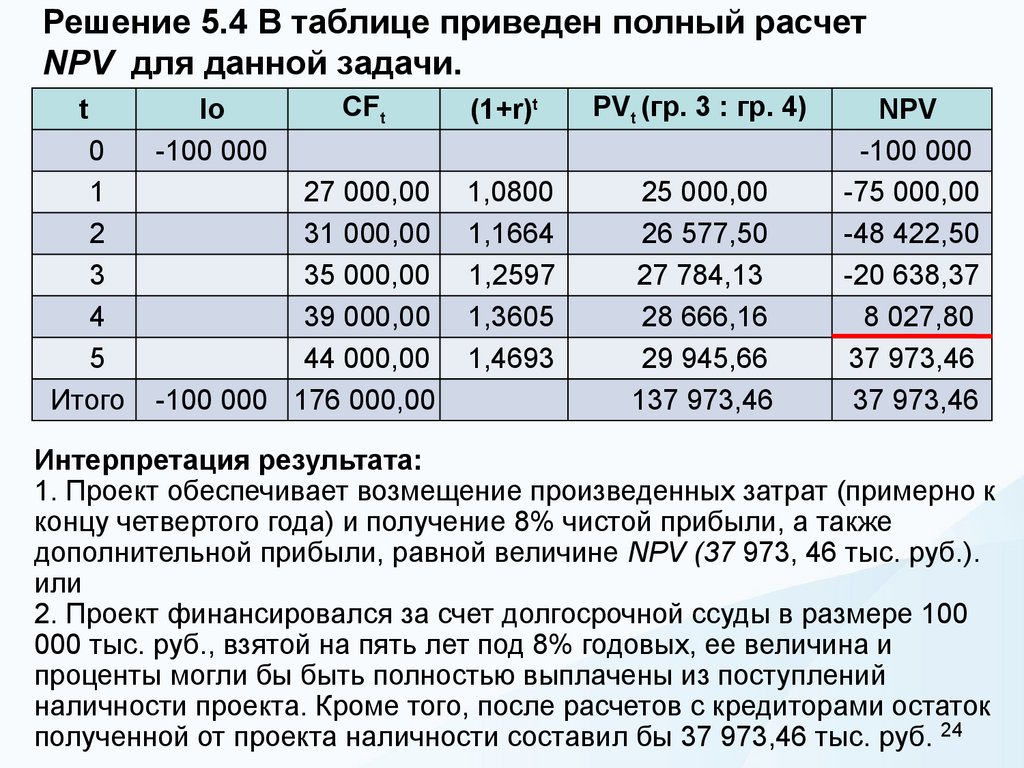
24. Решение 5.4 В таблице приведен полный расчет NPV для данной задачи.

t
0
1
2
3
4
5
Итого
Iо
-100 000
CFt
27 000,00
31 000,00
35 000,00
39 000,00
44 000,00
-100 000 176 000,00
(1+r)t
PVt (гр. 3 : гр. 4)
1,0800
1,1664
1,2597
1,3605
1,4693
25 000,00
26 577,50
27 784,13
28 666,16
29 945,66
137 973,46
NPV
-100 000
-75 000,00
-48 422,50
-20 638,37
8 027,80
37 973,46
37 973,46
Интерпретация результата:
1. Проект обеспечивает возмещение произведенных затрат (примерно к
концу четвертого года) и получение 8% чистой прибыли, а также
дополнительной прибыли, равной величине NPV (37 973, 46 тыс. руб.).
или
2. Проект финансировался за счет долгосрочной ссуды в размере 100
000 тыс. руб., взятой на пять лет под 8% годовых, ее величина и
проценты могли бы быть полностью выплачены из поступлений
наличности проекта. Кроме того, после расчетов с кредиторами остаток
полученной от проекта наличности составил бы 37 973,46 тыс. руб. 24

25. Чистая приведенная стоимость NPV

где:
• CF - денежные потоки в году t
• r - ставка дисконтирования
• t - порядковый номер года
• n - число лет до завершения проекта
• Критерий приемлемости инвестиций: NPV>0, т.е.
реализация проекта ведет к росту стоимости компании
Проблемы, возникающие при расчете NPV:
• моделирование денежных потоков;
• выбор ставки дисконтирования.
25

26.

Решение для Примера 5.5
Годы
0
1
2
3
4
Итого
Проект А
CF0 = -80
CF1 = 0
CF2 = 30
CF3 = 50
CF4 = 50
50
Проект В
CF0 = -50
CF1 = -10
CF2 = 60
CF3 = 30
CF4 = 10
40
К реализации принимается проект В
26

27. Ставка дисконтирования в условиях инфляции

p=r+i
• p - номинальная ставка дисконт-я в условиях инфляции
• r - реальная ставка дисконтирования
• i – темп инфляции
Пример 5.7 Рассматривается экономическая целесообразность
реализации проекта при следующих условиях: величина инвестиций — 5
000 тыс. руб.; период реализации про­екта — 3 года; доходы по годам (в
тыс. руб.): 2000, 2000, 2500; текущая ставка дисконтирования (без учета
инфляции) - 9,5%; среднегодовой темп инфляции — 5%.
Год
Денежный поток
0
-5 000
1
2000
2
2000
3
2500
27

28. Внутренняя норма доходности (IRR)

• Под внутренней нормой доходности понимают процентную ставку
(IRR), при которой NPV = 0.
• Внутренняя норма доходности определяется решением уравнения:
• Это уравнение решается относительно IRR каким-либо
итерационным методом.
28

29.

• В общем случае, чем выше величина IRR, тем больше
эффективность инвестиций.
• Величина IRR сравнивается с заданной ставкой дисконта r, при
этом:
- если IRR > r, проект обеспечивает положительную NPV и
доходность, равную (IRR — r).
- если IRR < r, затраты превышают доходы, и проект будет
убыточным.
• Общее правило IRR: если IRR > r, то проект принимается, иначе его
следует отклонить.
29

30.

Алгоритм определения IRR методом подбора можно представить
в следующем виде:
• выбирают произвольные ставки дисконтирования и рассчитывают
NPV;
• при одном значении ставок NPV отрицателен, при другом –
положителен;
• значения ставок и NPV включают в следующую формулу:
где:
r1 — дисконтная ставка, при которой NPV положителен;
r2 — дисконтная ставка, при которой NPV отрицателен;
NPV1 — величина положительного NPV;
NPV2 — величина отрицательного NPV.
30

31.

Пример 5.8 Требуется определить значение показателя IRR для
инвестиционного проекта, рассчитанного на четыре года, требующего
инвестиций в размере 15 млн руб. и имеющего предполагаемые
денежные поступления в размере 4,5 млн, 5,6 млн, 6,7 млн и 8,9 млн
руб.
31

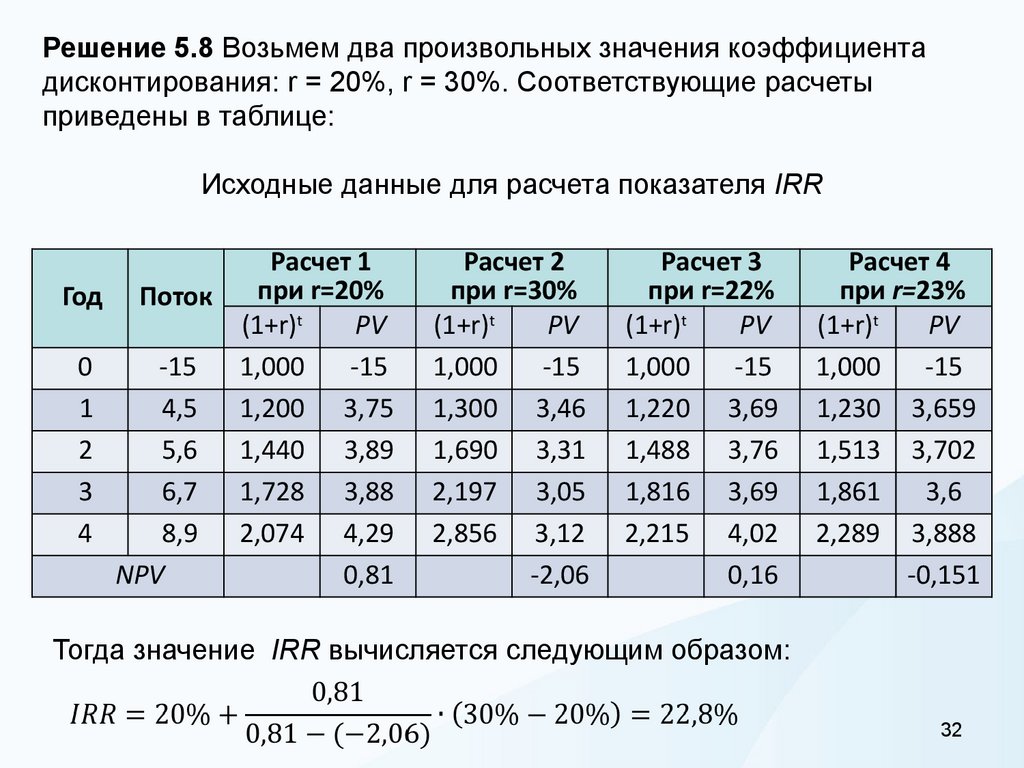
32.

Решение 5.8 Возьмем два произвольных значения коэффициента
дисконтирования: r = 20%, r = 30%. Соответствующие расчеты
приведены в таблице:
Исходные данные для расчета показателя IRR
Расчет 1
при r=20%
Год Поток
(1+r)t
PV
0
-15
1,000
-15
1
4,5 1,200 3,75
2
5,6 1,440 3,89
3
6,7 1,728 3,88
4
8,9 2,074 4,29
NPV
0,81
Расчет 2
при r=30%
(1+r)t
PV
1,000
-15
1,300 3,46
1,690 3,31
2,197 3,05
2,856 3,12
-2,06
Расчет 3
при r=22%
(1+r)t
PV
1,000
-15
1,220 3,69
1,488 3,76
1,816 3,69
2,215 4,02
0,16
Расчет 4
при r=23%
(1+r)t
PV
1,000
-15
1,230 3,659
1,513 3,702
1,861
3,6
2,289 3,888
-0,151
Тогда значение IRR вычисляется следующим образом:
32

33.

• Можно уточнить полученное значение. Допустим, что путем
нескольких итераций мы определили ближайшие целые значения
коэффициента дисконтирования при которых NPV меняет знак:
• При r = 22% NPV = +0,16; при r = 23% NPV = -0,15.
• Тогда уточненное значение IRR будет равно:
• Истинное значение показателя IRR равно 22,5%, т. е. метод
последовательных итераций обеспечивает весьма высокую точность.
33

34. Срок окупаемости, простой (РР)

• PP (Pay-back Period ) - простой срок окупаемости - это число лет, в
течение которых совокупные денежные потоки, генерируемые
проектом, покрывают инвестиционные затраты.
• Срок окупаемости при равномерном поступлении денежных
средств рассчитывается по формуле:
где:
• I0
• CF
- первоначальные инвестиции;
- годичная сумма поступлений от реализации проекта.
34

35.

• Период (срок) окупаемости (payback period, PB) — минимальный
временной интервал (измеряемый в месяцах или годах) от начала
осуществления проекта (от начала инвестиционной стадии, от
момента t=0) до окончания срока, за который инвестиционные
затраты покрываются порождаемыми ими денежными
поступлениями.
• Пример
Инвестиции по
Операционные денежные потоки
годам
по проекту (OCF)
20
40
10 30
50
90
90
90
100
Инвестиционная стадия проекта = 3 года (в начальный момент инвестируем
20, потом на конец каждого года фиксируются инвестиции в 40, 10 и 30
денежных единиц).
Суммарные инвестиции равны 100.
В четвертый год проект не окупится: 50<100. В пятый год проект окупится.
Если денежные потоки приходят в конце года, то срок окупаемости = 5 лет.
Если денежные потоки поступают равномерно по кварталам (приходят в
конце квартала), то каждый квартал придет поток в 22,5.
По окончании 4 года не окупившаяся сумма равна 50. За 2 квартала нужная

36. Срок окупаемости, простой (РР)

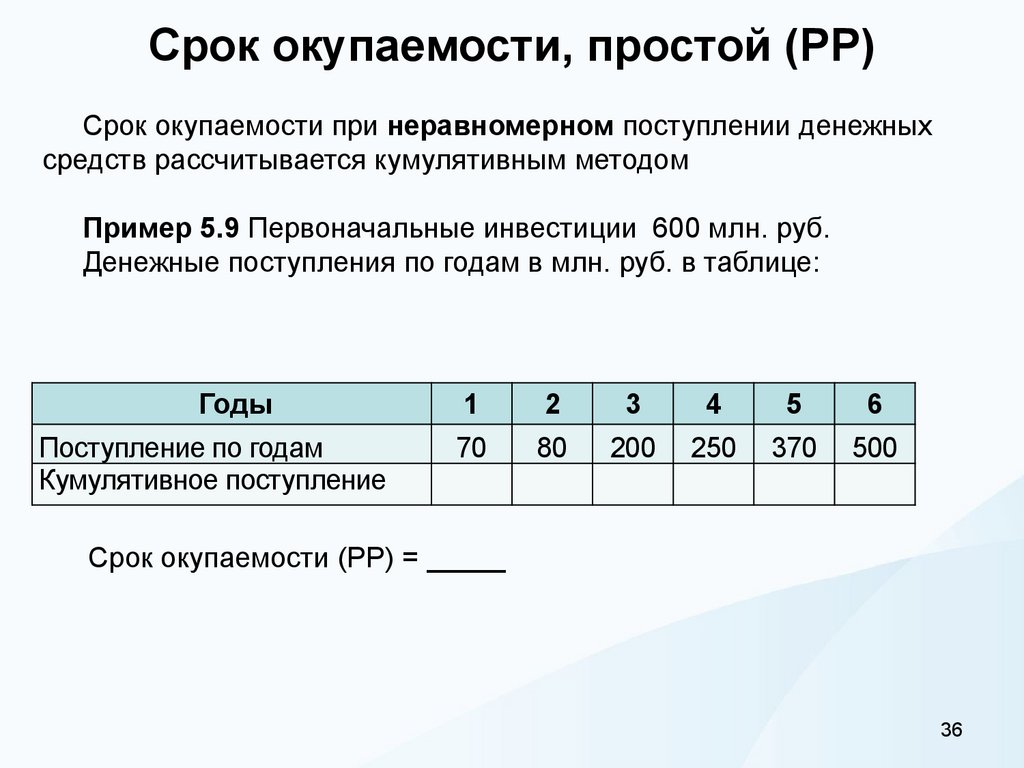
Срок окупаемости при неравномерном поступлении денежных
средств рассчитывается кумулятивным методом
Пример 5.9 Первоначальные инвестиции 600 млн. руб.
Денежные поступления по годам в млн. руб. в таблице:
Годы
Поступление по годам
Кумулятивное поступление
1
2
3
4
5
6
70
80
200
250
370
500
Срок окупаемости (РР) = _____
36

37. Срок окупаемости, дисконтированный (DPP)

• Дисконтированный срок окупаемости (Discounted Payback Period,
DPP) – период возврата денежных средств инвестированных в
проект за счет чистого денежного потока создаваемого этими
инвестициями, приведенных по фактору времени
(дисконтированных) к настоящему моменту.
где:
DPP – дисконтированный срок окупаемости инвестиций;
IC (Invest Capital) – первоначальные инвестиционные затраты в
проекте;
CF (Cash Flow) – денежный поток, создаваемый инвестицией;
r
– ставка дисконтирования;
n
– срок реализации проекта.

38. Срок окупаемости, дисконтированный (DPP)

Дисконтированный срок окупаемости (Discounted Pay-Back Period,
DPP) — это срок, требуемый для возврата вложенных инвестиций в
проект за счёт чистого денежного потока создаваемого этими
инвестициями с учётом ставки дисконтирования.
Дисконтированный срок окупаемости (DPP) рассчитывается прямым
подсчетом числа лeт, в течение которых инвестиция будет погашена
кумулятивным дисконтированным доходом:
где:
DPP – дисконтированный срок окупаемости инвестиций;
IC (Invest Capital) – первоначальные инвестиционные затраты в
проекте;
DCFt – дисконтированный денежный поток;
n
– число лeт, в течение которых первоначальные инвестиции
38
будут погашены.

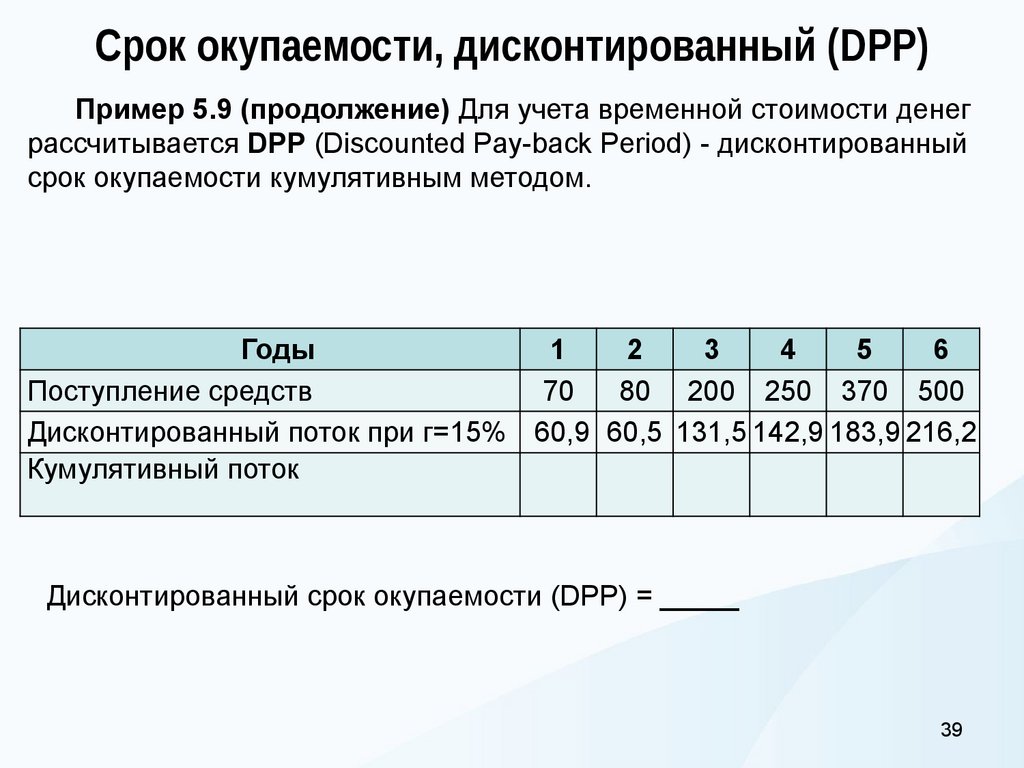
39. Срок окупаемости, дисконтированный (DPP)

Пример 5.9 (продолжение) Для учета временной стоимости денег
рассчитывается DPP (Discounted Pay-back Period) - дисконтированный
срок окупаемости кумулятивным методом.
Годы
1
2
3
4
5
6
Поступление средств
70
80 200 250 370 500
Дисконтированный поток при г=15% 60,9 60,5 131,5 142,9 183,9 216,2
Кумулятивный поток
Дисконтированный срок окупаемости (DPP) = _____
39

40. Индекс прибыльности инвестиций (PI)

40