Similar presentations:
20 Лекция 20 перех процесс цепи 1 порядка
1. 13 лекция
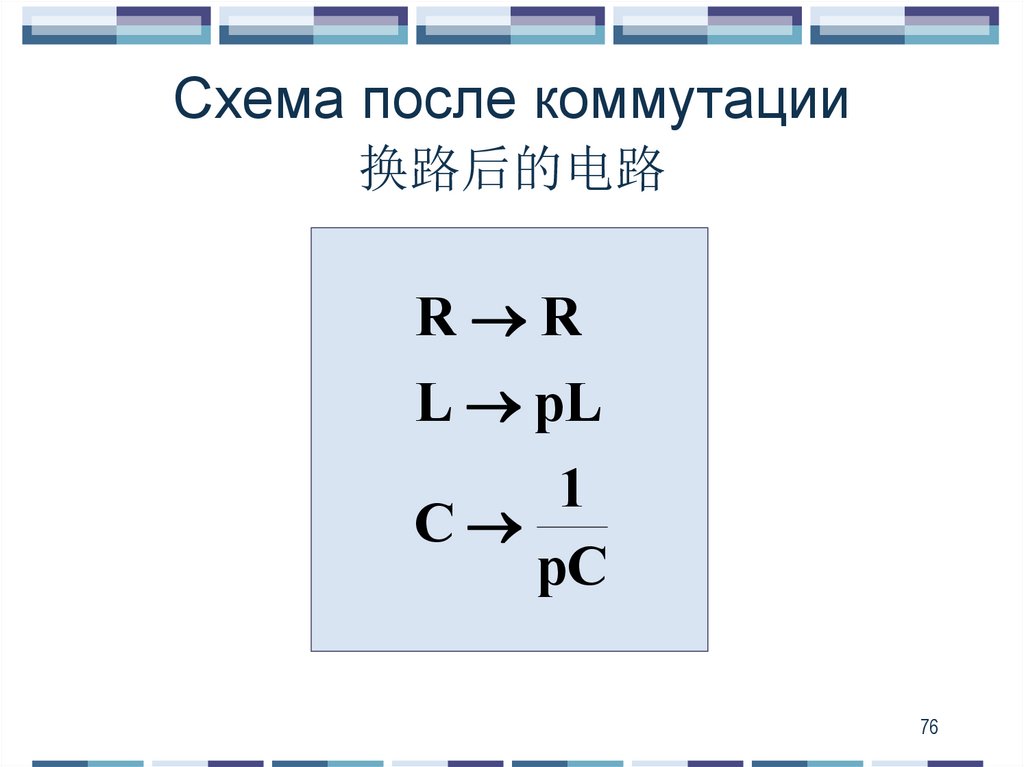
2. Классический метод расчета переходных процессов 过渡过程的经典计算方法
23.
Классический методоснован на решении линейного
дифференциального уравнения
переходного процесса
经典法以求解过渡过程的线性微
分方程为基础
3
4.
Такое уравнениесоставляется при помощи
законов Кирхгофа
для цепи после
коммутации
这方程是在基尔霍夫定律的基础
上建立的(对于换路后的电路)
4
5. Линейная цепь первого порядка 一阶(线性)电路
56.
Содержитпосле коммутации
L или С
换路后含有L或C
6
7. Характеризуется линейным дифференциальным уравнением 1-го порядка 一阶线性常微分方程
df (t )a1
a 0f ( t ) F ( t )
dt
7
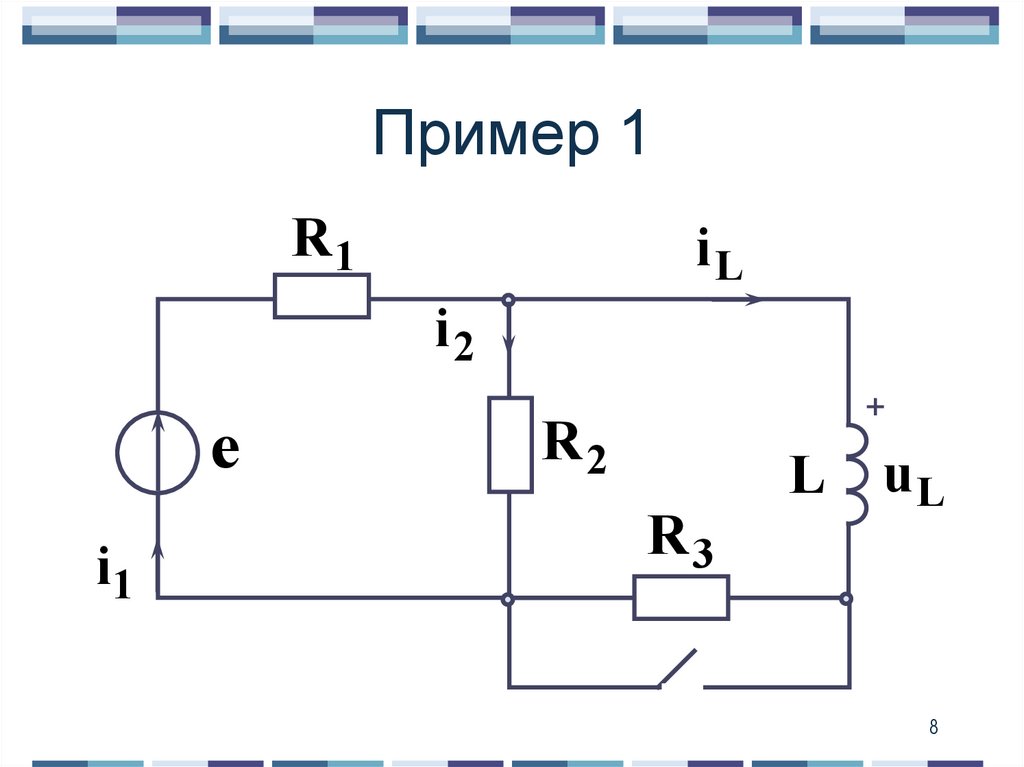
8. Пример 1
R1iL
i2
е
i1
+
R2
R3
L uL
8
9. Дано(已知):
е 100 ВL 1 Гн
R1 100 Ом
R 2 25 Ом
R 3 100 Ом
Определить:
i1 ( t ) ?
9
10. Для схемы после коммутации 对于换路之后的电路:
(1)i 1 i 2 i L
e R 1i1 u L ( 2)
0 R i u ( 3 )
2 2
L
di L
Причём并且 u L L
dt
10
11. Из 2 уравнения 由方程2:
1iL
(e R 1i1 )dt
L
( 4)
11
12. Из 3 и 4 уравнений 由方程3和4:
L di L e R1i1i2
R 2 dt
R2
( 5)
12
13. Из уравнений 1, 4, 5: 由方程1,4,5:
Из уравнений 1, 4, 5:由方程1,4,5
e R1i1 1
i1
(e R1i1 ) dt
R2
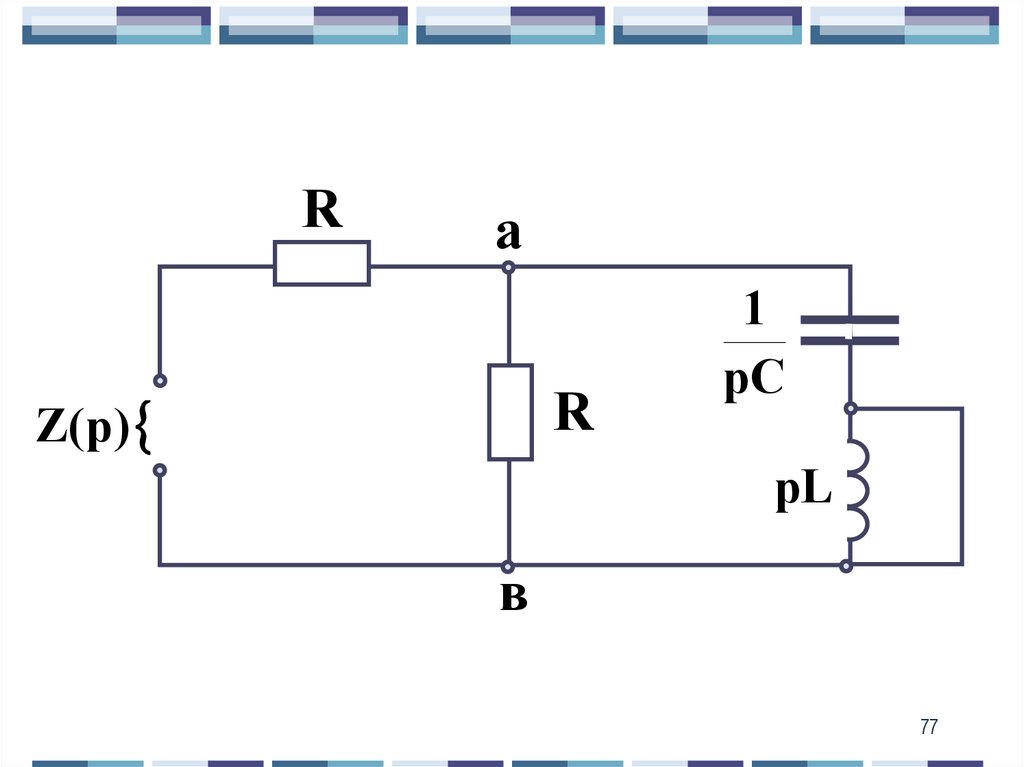
L
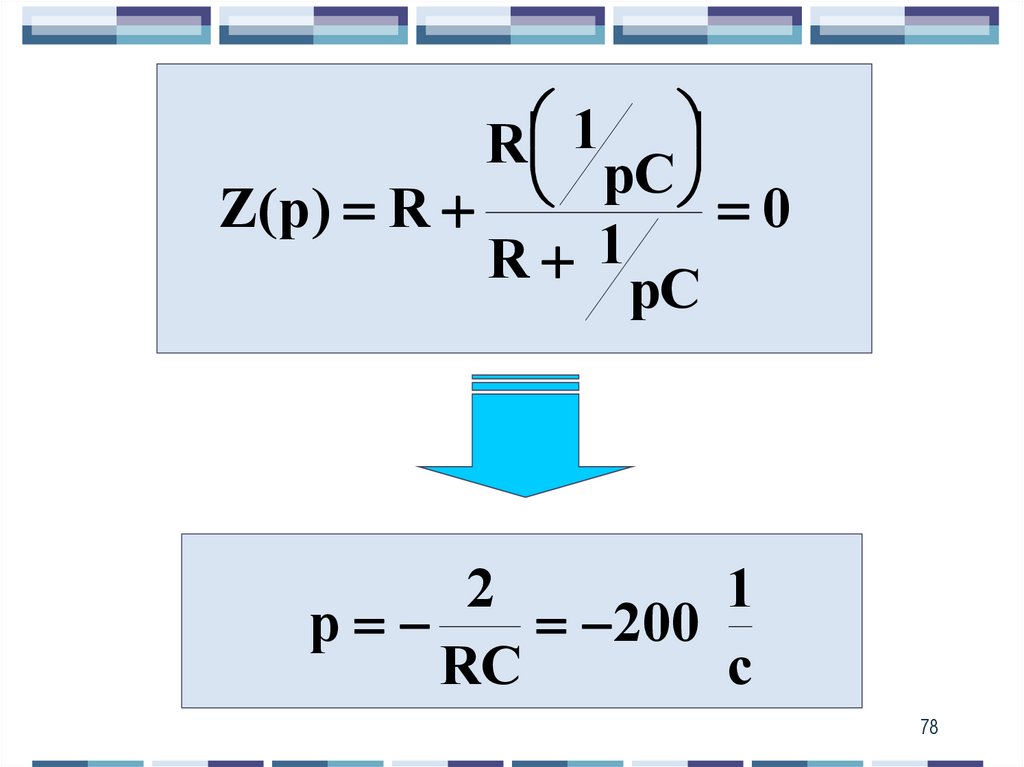
(6)
13
14. Дифференцируем 6 уравнение 对方程6求微分:
di 11 de R1 di 1 e R1
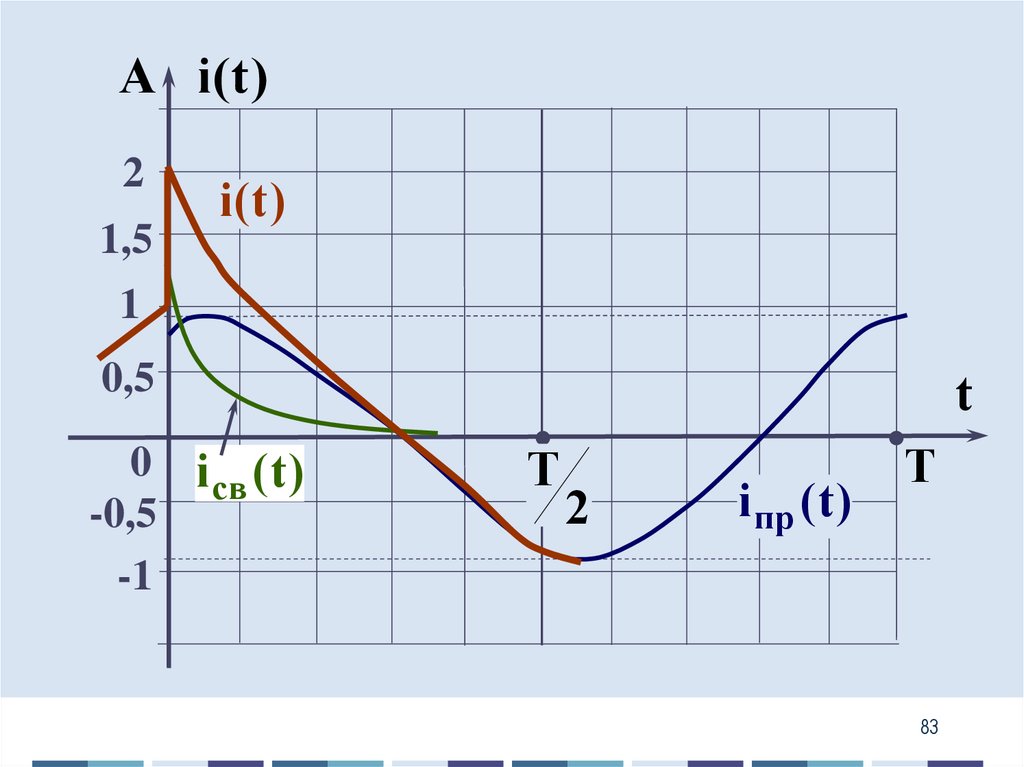
i1 (7)
dt R 2 dt R 2 dt L L
14
15. Преобразуем уравнение 7 移项化简方程7:
R1 di 1L de
L(1
)
R1i1 e
(8)
R 2 dt
R 2 dt
15
16. Таким образом 用这种方法
R1а1 L(1
) 5 Гн
R2
а0 R1 100 Ом
0
L de
F( t ) e
100 B
R 2 dt
16
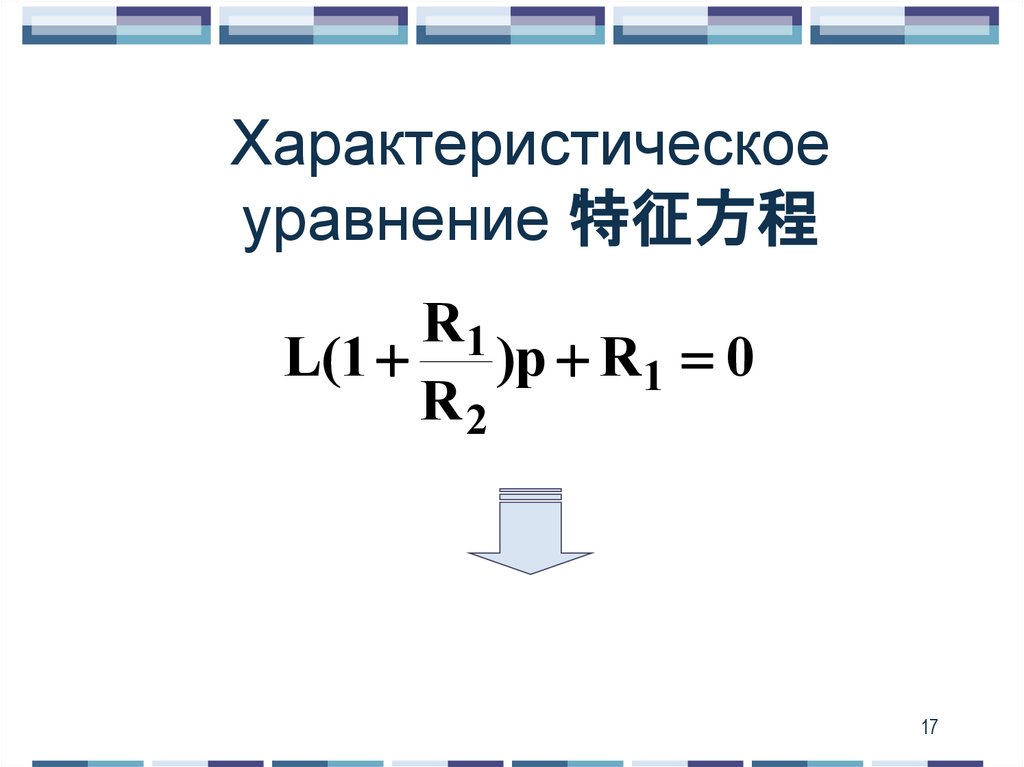
17. Характеристическое уравнение 特征方程
R1L(1
)p R1 0
R2
17
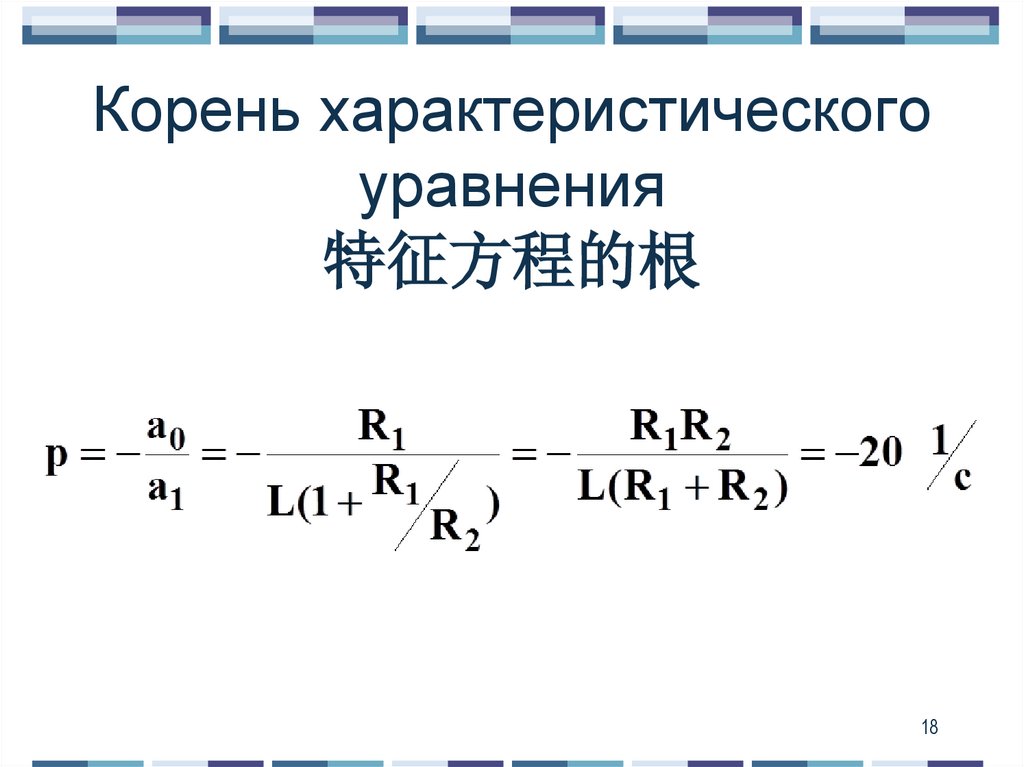
18. Корень характеристического уравнения 特征方程的根
1819. Корень p 特征方程的根 можно найти при помощи Z(p) – сопротивления относительно любой ветви после коммутации
1920. Рисуем схему в которой заменяем 画出电路图,在该电路中做以上替换 Размыкаем цепь в любом месте и определяем Z(p)=…..=0 在任何地方断开电路并且定义Z(p)=…..=0
Рисуем схему в которойзаменяем 1
R R, L pL, C
pC
E R Е 0, J R J
画出电路图 在该电路中做以上替换
Размыкаем цепь
в любом месте и определяем
Z(p)=…..=0
在任何地方断开电路并且定义Z(p)=…..=0
20
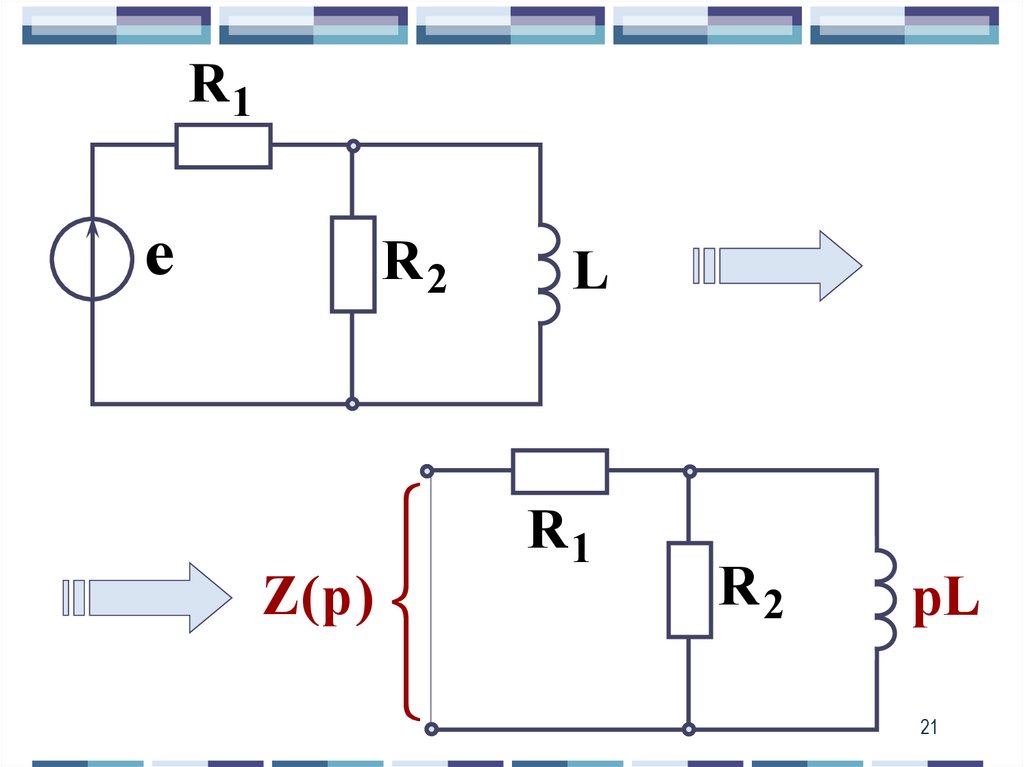
21.
R1е
R2
L
Z(p )
R1
R2
рL
21
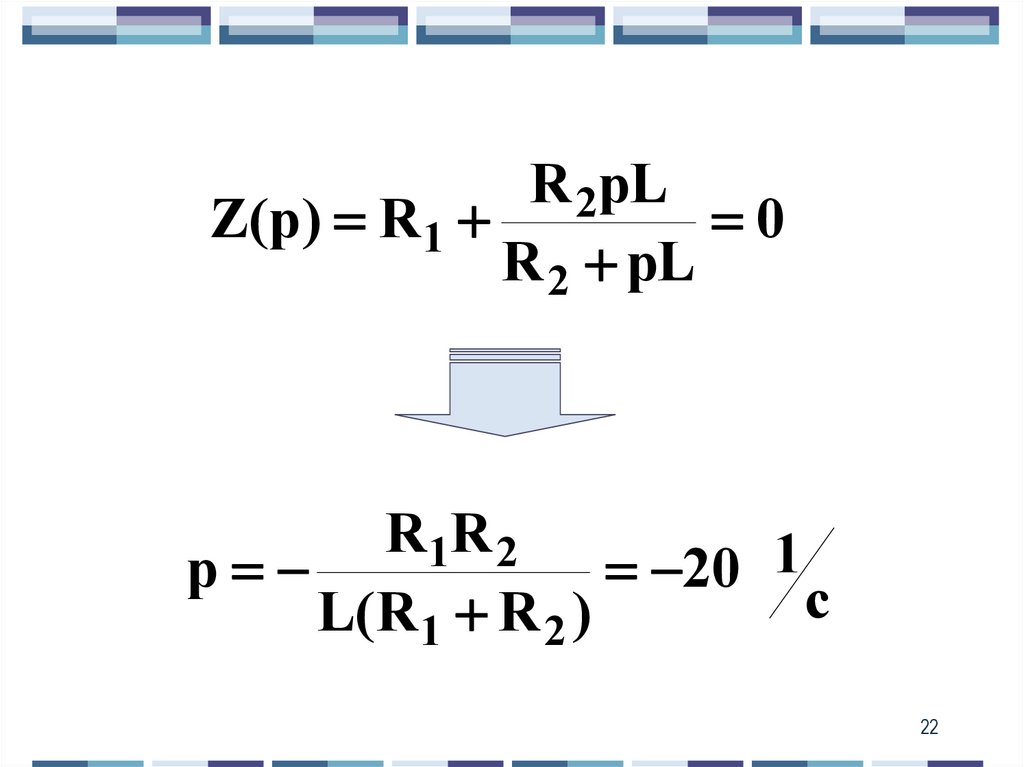
22.
R 2pLZ(p ) R1
0
R 2 pL
R 1R 2
p
20 1
c
L( R1 R 2 )
22
23. Решение уравнения 8:
i1 (t) i пр1 (t) i св1 (t)i пр1 (t) Ae
pt
23
24. - принужденная составляющая 强制分量
i пр1 (t) - принужденнаясоставляющая 强制分量
i св1 (t) Ae - свободная
pt
составляющая
自由分量
А - постоянная
интегрирования 积分常数
24
25. Т.к.
F(t ) 100 B const ,то
i пр (t ) I пр const
1
1
25
26. Подставим в уравнение 8 将 带入方程8:
IПодставим пр1 в уравнение 8
将 I пр 带入方程8:
1
0
R1 dI пр1
L de
L(1
)
R1I пр1 e
R 2 dt
R 2 dt
0
т.е.
е
I пр1
1 A
R1
26
27. (强制分量)можно найти расчетом схемы при
I пр (强制分量)можно найти1
расчетом схемы при
t
27
28. В цепи постоянного тока (在直流电路中 )заменяем
L R L 0, C R C28
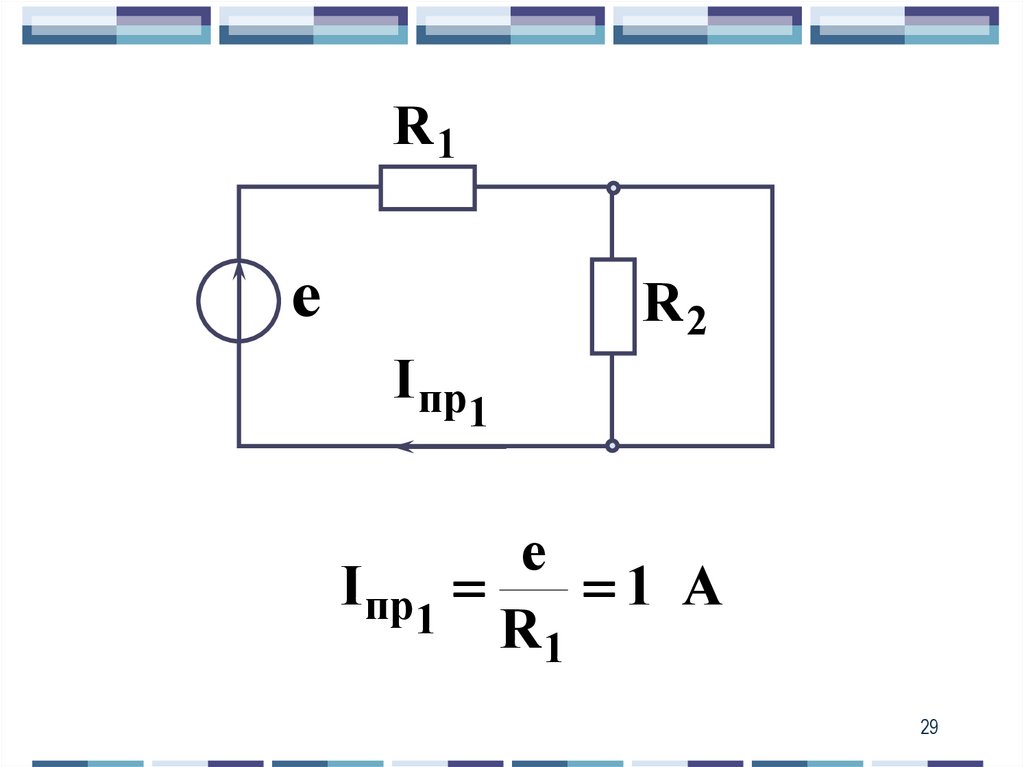
29.
R1е
R2
I пр
1
е
I пр
1 A
1 R
1
29
30. Постоянная интегрирования 积分常数
А i1 (0) i пр (0) i1 (0 ) I пр1
1
30
31. Для расчета А определяются начальные условия 初始条件
3132.
Различают:а) независимые начальные
условия (нну) 独立初始条件
i L (0) i L (0 ) i L (0 )
и
u C (0) u C (0 ) u C (0 )
32
33. нну (独立初始条件) определяются из расчёта схемы до коммутации в момент времени
t 033
34.
б) зависимые начальныеусловия (зну) 相关初始条件
iС (0 ), uL (0 )
и другие величины
34
35. зну (相关初始条件) определяются из расчета схемы после коммутации в момент времени
t 035
36. Для расчета зну рисуем схему в которой заменяем L на источник тока 将电感L替换成电流源
J i L (0)C заменяем на источник ЭДС
将电容C替换成电压源
E u C (0)
36
37. Для примера 1 получим: 对于例子1我们可以得到:
Для примера 1 получим:对于例子1我们可以得到
37
38.
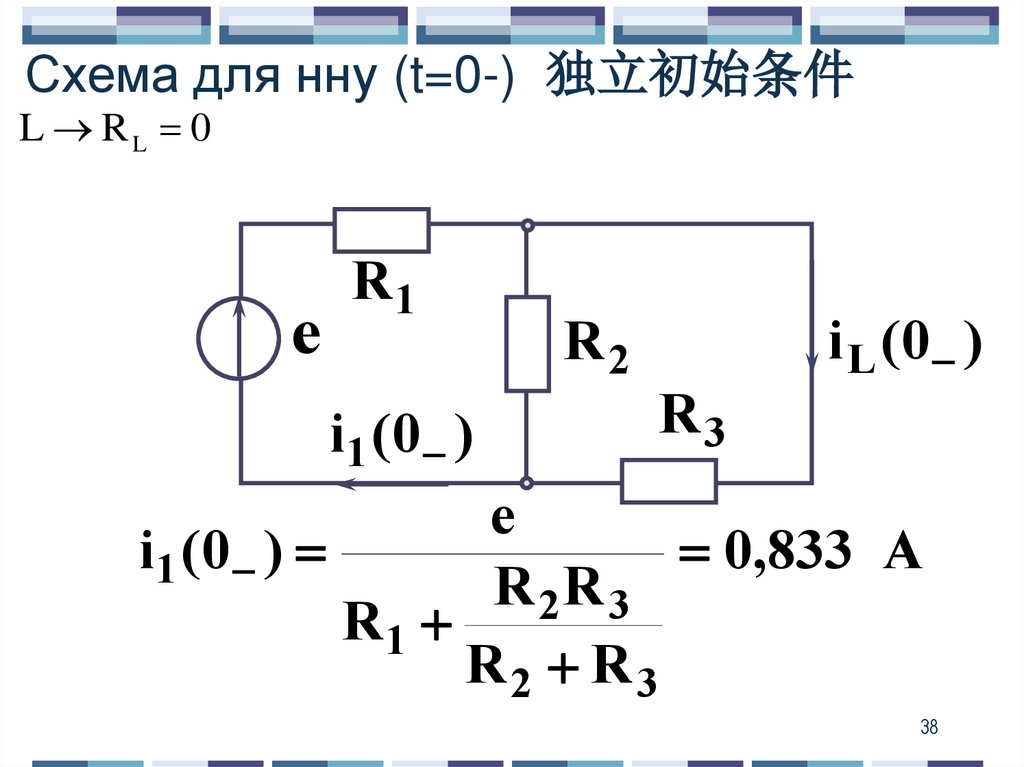
Схема для нну (t=0-) 独立初始条件L RL 0
е
R1
i1 (0 )
R2
R3
i L (0 )
е
i1 (0 )
0,833 A
R 2R 3
R1
R2 R3
38
39.
По правилу разброса тока в параллельных ветвях:R2
i L (0 ) i1 (0 )
0,167 A
R2 R3
- нну 独立初始条件
39
40.
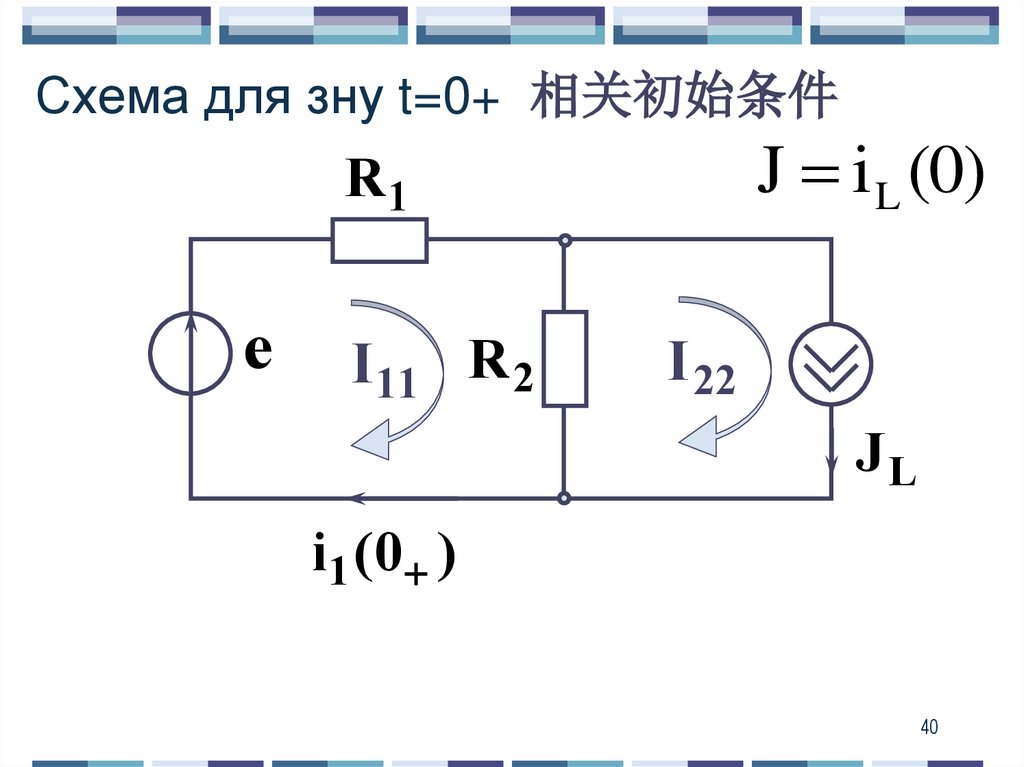
Схема для зну t=0+ 相关初始条件J i L (0)
R1
е
I11 R 2
I 22
JL
i1 (0 )
40
41.
J L i L (0 ) i L (0 ) 0,167 AI 22 J L
I11 ( R1 R 2 ) I 22 R 2 e
41
42.
e JLR 2i1 (0 ) I11
0,833 A
R1 R 2
- зну 相关初始条件
Постоянная интегрирования
积分常数:
А i1 (0 ) I пр1 0,167 А
42
43.
Ответ:t
20t
i1 (t ) 1 0,167e
1 0,167e
где
A
1
1
p
0,05 c
20
- постоянная времени
时间常数
43
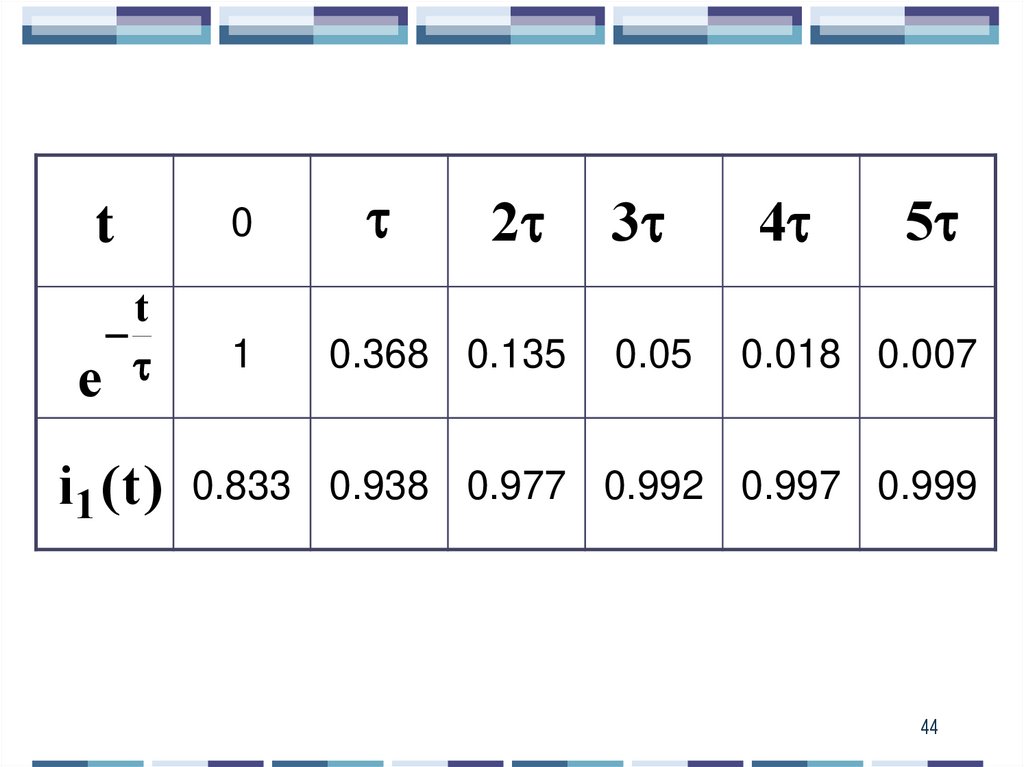
44.
t0
t
е
1
5
2
3
4
0.368 0.135
0.05
0.018 0.007
i1 ( t ) 0.833 0.938 0.977 0.992 0.997 0.999
44
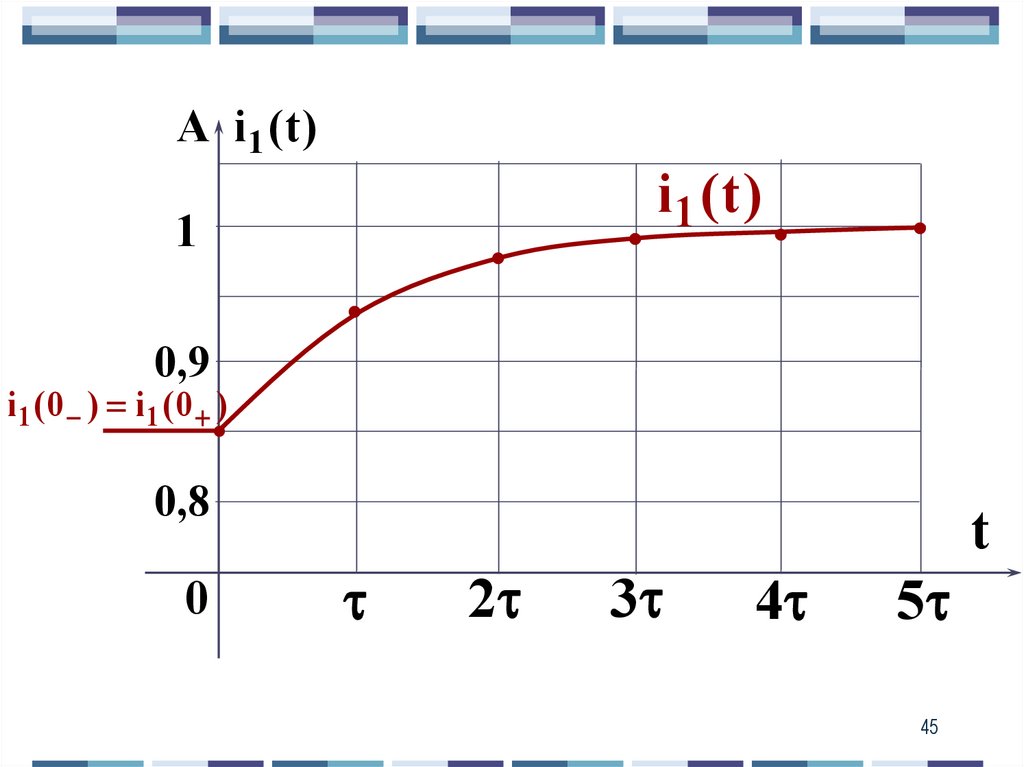
45.
А i1 (t )i1 (t )
1
0,9
i1 (0 ) i1 (0 )
0,8
0
2
3
t
4
5
45
46. Длительность переходного процесса 过渡过程持续时间 равна tП = 5
4647. Порядок расчёта классическим методом цепи 1 порядка 用经典法求解一阶电路的步骤
4748. Определяем ННУ 独立初始条件 при :
1. Определяем ННУ独立初始条件
при t 0 :
i L (0 )
или
uC (0 )
48
49. 2. Определяем ЗНУ 相关初始条件 при :
2. Определяем ЗНУ相关初始条件
при t 0 :
u L (0 ), i C (0 )
и другие напряжения и
токи
49
50. 3. Определяем принужденные составляющие при t=∞ 当t=∞时,确定强迫分量
3. Определяемпринужденные
составляющие
при t=∞
当t=∞时 确定强迫分量
50
51. Определяется корень 特征方程的根 p по
4. Определяется корень特征方程的根 p
по
Z(p) ... 0
51
52. 5. Определяем постоянную интегрирования 积分常数 А или В при :
5. Определяем постояннуюинтегрирования 积分常数
А или В при t 0 :
А i(0 ) i пр (0)
В u(0 ) uпр (0)
52
53. 6. Записываем ответ
i(t ) i пр (t ) Aept
u(t ) uпр (t ) Ве
pt
53
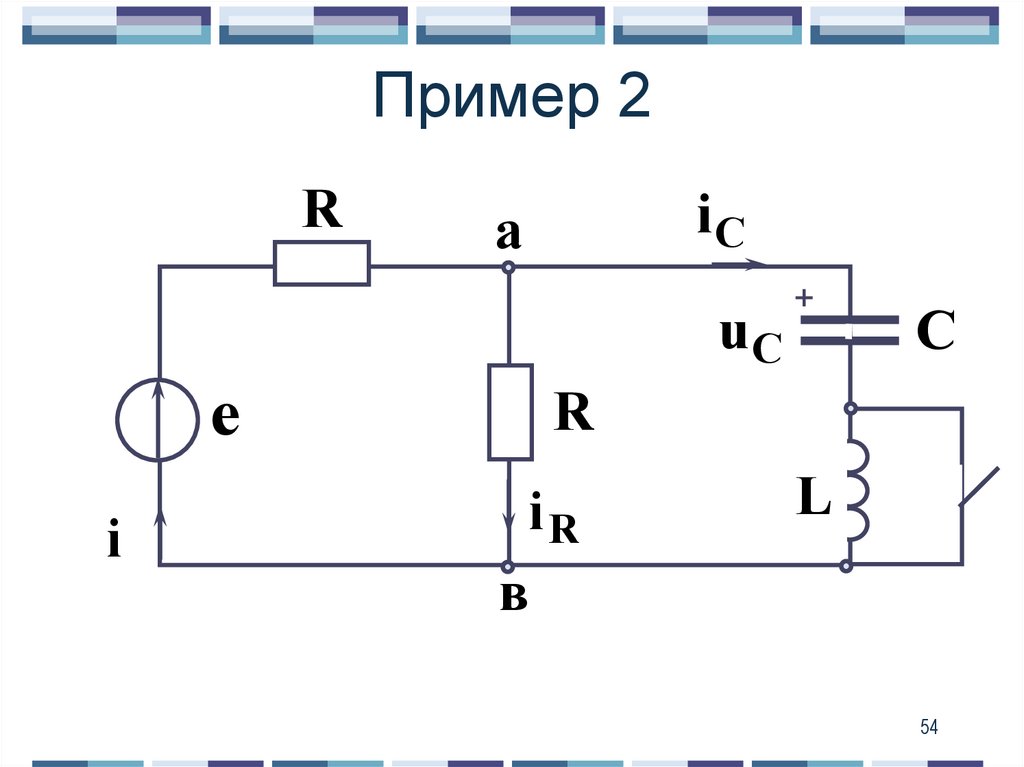
54. Пример 2
RiС
а
uC
е
i
+
С
R
iR
в
L
54
55. Дано已知:
е 100 2 sin(100t 45 ), BR 100 Ом
L 1 Гн
С 100 мкФ
55
56. Определить:
i( t ) ?56
57. 1. Определяем нну 独立初始条件:
i L (0 ) ?uC (0 ) ?
57
58. Расчет схемы до коммутации ведем символическим методом 使用符号法求解换路之前的电路
5859.
X L L 100 Ом1
ХС
100 Ом
С
Е 100е
j45
B
59
60. Т.к.
(Д)Zав jXL jXC 0
то
E
(Д)
(Д)
j45
I С I L 1e
A
(Д)
j45
U C ( jXC )I C 100e
B
I
(Д)
R
60
61. В результате 最终:
В результате 最终(Д)
iL
( Д)
uC
2 sin(100t 45 ), A
2 100 sin(100t 45 ), B
61
62. Тогда
( Д)i L ( 0 ) i L ( 0)
2 sin 45 1 A
( Д)
u C ( 0 ) u C ( 0)
2 100 sin( 45 ) 100 B
62
63. Причем 并且
i( 0 ) i L ( 0 ) 1 A63
64. 2. Определим зну 相关初始条件:
i( 0 ) ?64
65. Схема после коммутации в момент: 换路后的瞬间
t 065
66.
J L i L (0 ) i L (0 ) 1 AEC uC (0 ) uC (0 ) 100 В
е(0) 2 100 sin 45 100 B
66
67.
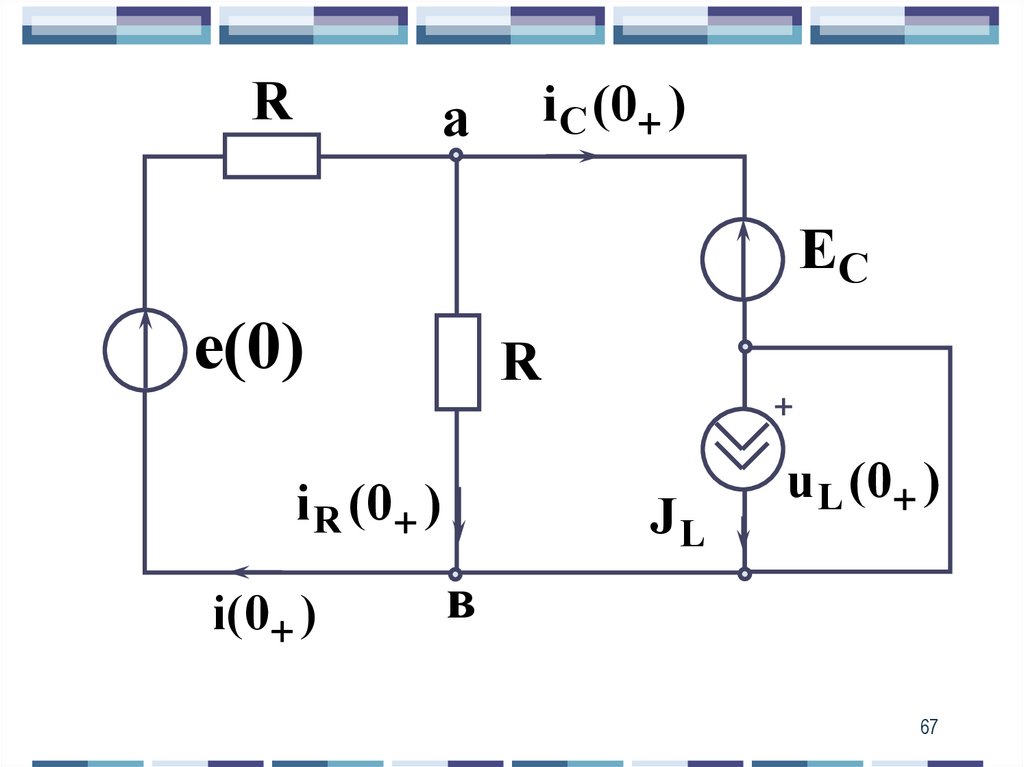
Ri С (0 )
а
EC
е(0)
R
i R (0 )
i( 0 )
+
JL
u L (0 )
в
67
68. Т.к. то
Т.к.u L (0 ) 0,
то
e(0) EC R i(0 )
68
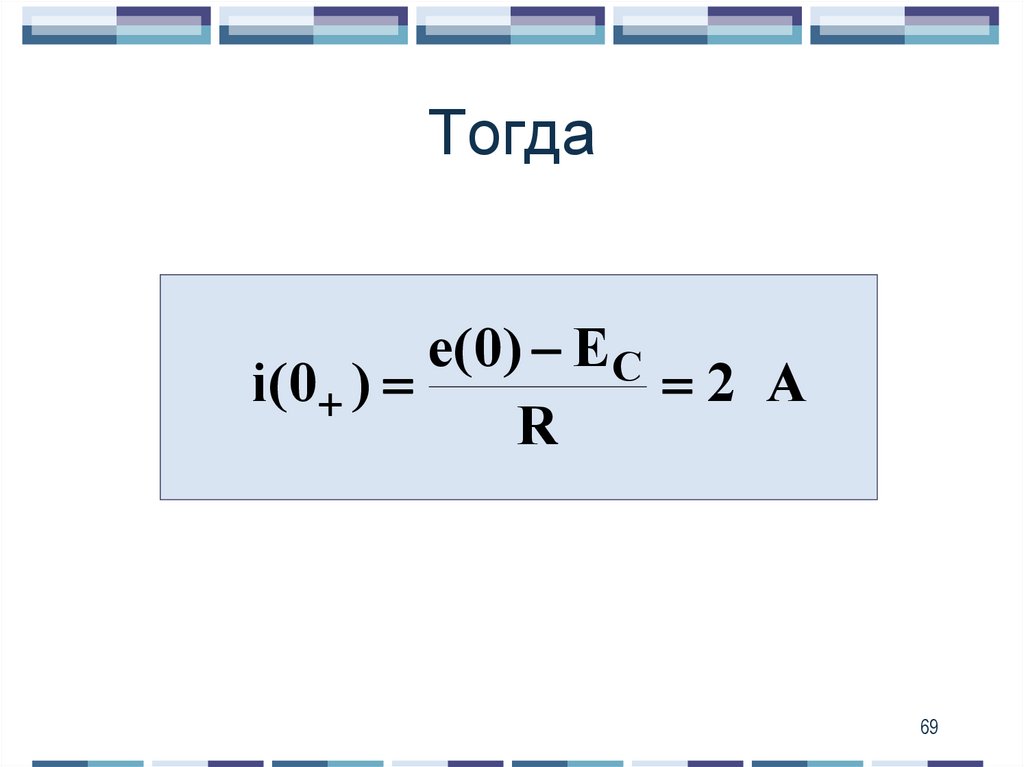
69. Тогда
e(0) ECi( 0 )
2 A
R
69
70. 3. Определим принужденную составляющую 强迫分量:
i пр (t ) ?70
71. Расчет принужденной составляющей ведём символическим методом 使用符号法求解强迫分量
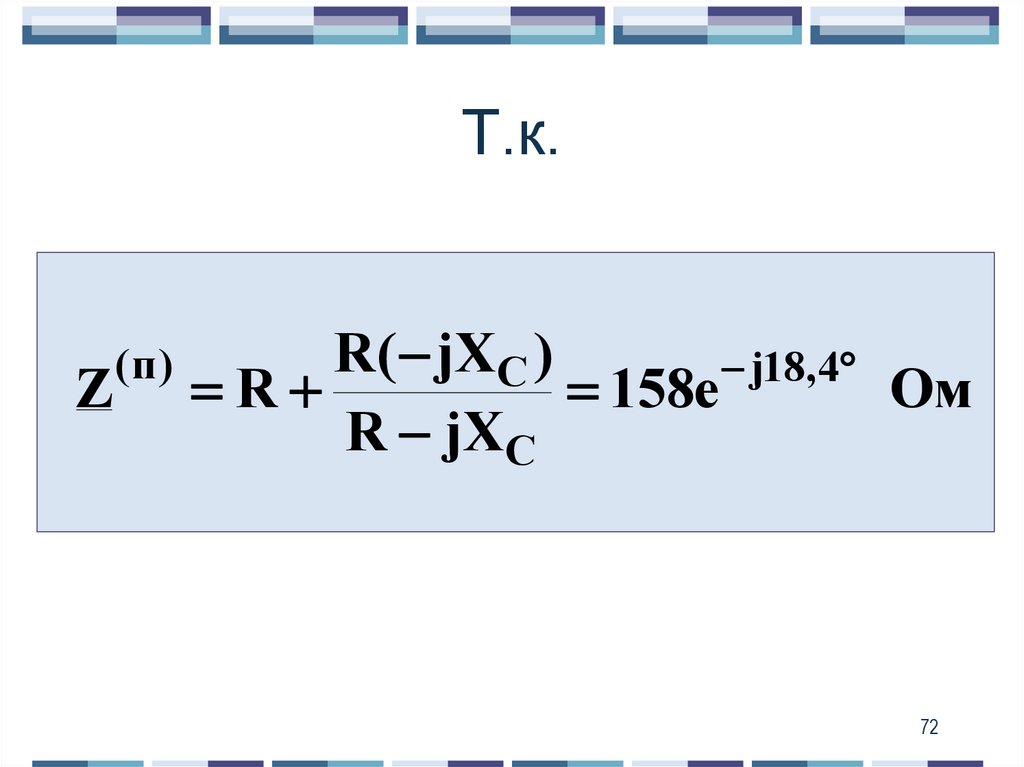
7172. Т.к.
Z(п)
R( jXC )
j18,4
R
158e
Ом
R jXC
72
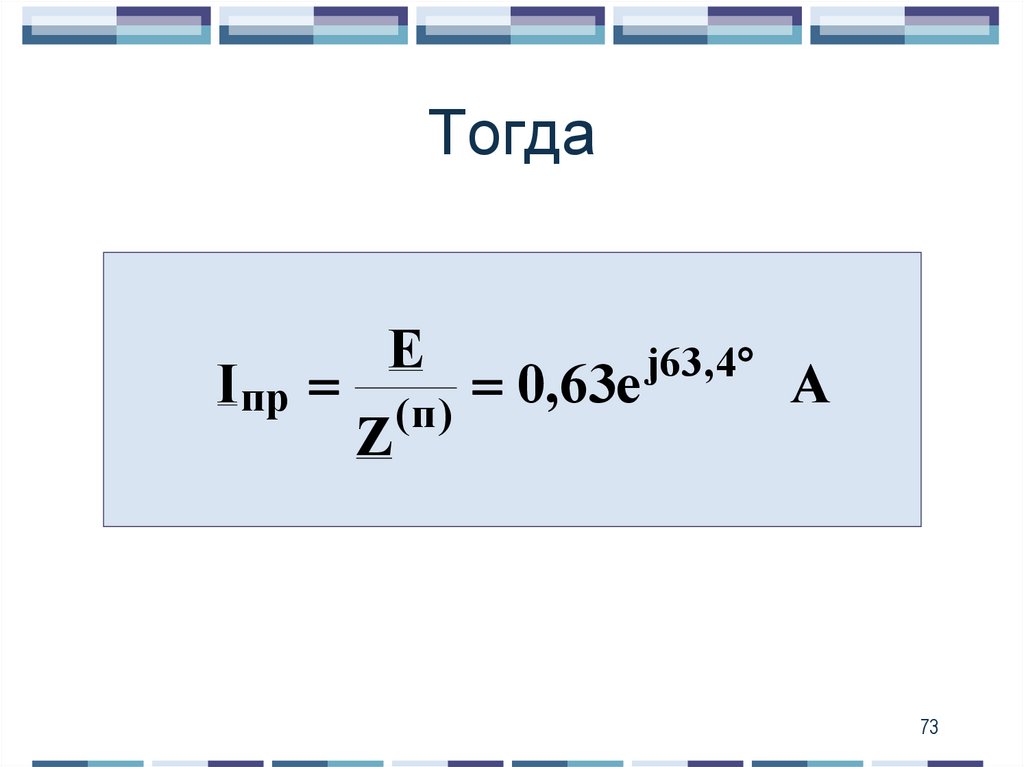
73. Тогда
I прЕ
Z
0
,
63
е
(п)
j63,4
A
73
74. В результате причем
В результатеi пр (t ) 2 0,63 sin(100t 63,4 ) A
причем
i пр (0) 2 0,63 sin 63,4 0,794 A
74
75. 4. Определяем корень характеристического уравнения 特征方程的根:
р ?75
76. Схема после коммутации 换路后的电路
R RL pL
1
C
pC
76
77.
Rа
R
Z(p )
1
рС
рL
в
77
78.
R 1pC
Z( p ) R
0
R 1
pC
2
1
p
200
RC
c
78
79. 5. Находим постоянную интегрирования 求出积分常数:
A i(0 ) i пр (0) 2 0,794 1,206 А79
80. 6. Ответ:
i(t ) i пр (t ) i св (t ) i пр (t ) Aept
80
81. Или
i(t ) 2 0,63 sin(100t 63,4 )1,206е
200t
A
81
82. Причем
13
5 10 (с)
р
2
t п 5 2,5 10 (c)
2
2
Т
6,28 10 (с)
82
83.
А i( t )2
1,5
i( t )
1
0,5
0 i (t )
св
-0,5
-1
t
Т
2
i пр ( t )
Т
83
































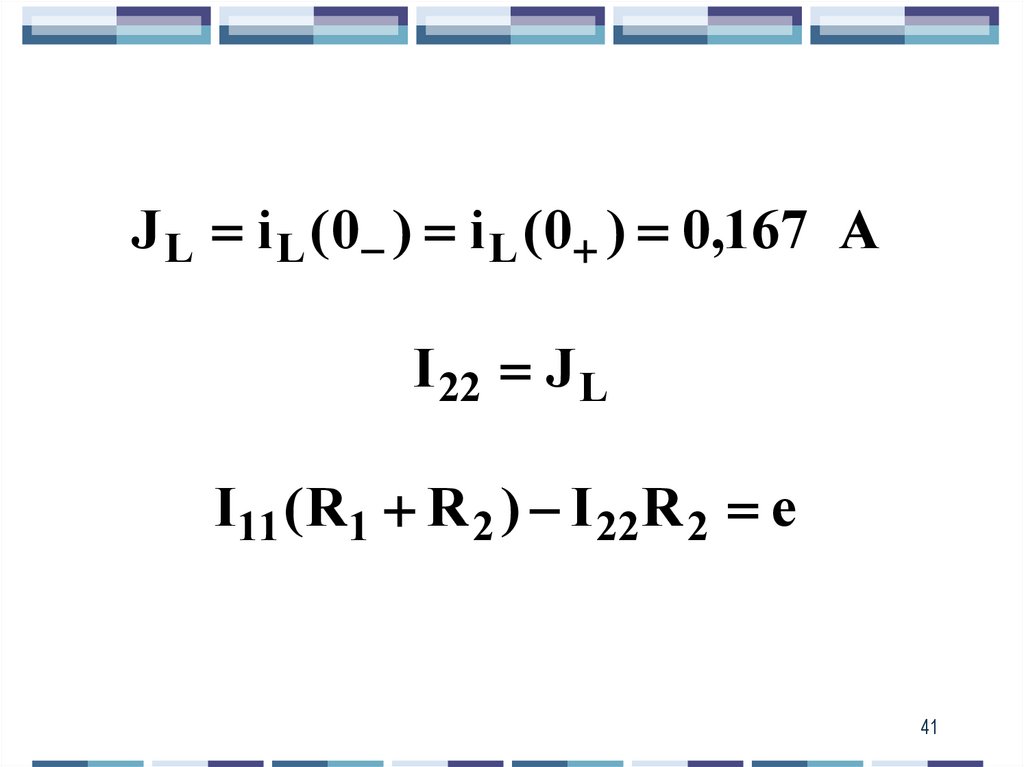































 industry
industry








