Презентация Своя Игра по теме теория вероятности

1.

2.

Задача каждой команды набрать как
можно большее количество баллов.
Для этого необходимо правильно
ответить на вопросы
отборочных
туров и в финальной игре не только
правильно ответить, но и сделать
большую ставку на свой ответ. Подсчёт
набранных баллов ведёт счётная
комиссия и отображает результаты на
табло.

3.

В отборочных турах каждый вопрос имеет
свою стоимость, на обдумывание дается
одна минута, отвечает та команда, которая
быстрее поднимет руку. Если команда
ответила верно баллы прибавляются, если
неверно баллы отнимаются.
Если команда ответила правильно, то она
выбирает следующий вопрос, если неверно
право выбора вопроса переходит к другой
команде.

4.

На вопрос – аукцион право ответа
имеет та команда, которая назначит
большую сумму, если на счету игроков
сумма,
меньшая
чем
стоимость
вопроса, то они могут предложить
только номинал (стоимость вопроса).
На вопрос кот в мешке отвечает та
команда, которой отдает это право
команда, выбравшая вопрос.

5.

«Своя игра»

6. 1 раунд

7.

Математические
термины
10
20
30
40
50
Формулы теории
вероятности
10
20
30
40
50
Крылатые фразы
10
20
30
40
50
Задачи о выборе
объектов из набора
10
20
30
40
50
Задачи о пересечении
независимых событий
10
20
30
40
50
Задачи о
противоположном
событии
10
20
30
40
50

8. Математические термины 10

Случайным называется событие……..

9. Математические термины 10

Случайным называют событие,
которое может произойти или не
произойти во время испытания

10. Математические термины 20

Вероятностью события А называется ……

11. 20

Вероятностью события А
называется отношение числа
благоприятных для этого
события исходов к общему числу
равновозможных исходов

12. термины 30

События А и В называют
Противоположными……

13. термины 30

События А и В называются
противоположными друг другу ,если
любой исход благоприятен ровно для
одного из них

14. термины 40

События А и В называют …….,если
отсутствуют исходы ,
Благоприятствующие одновременно
как событию А, так и событию В

15. Термины 40

несовместными.

16. Математические термины 50

Пусть событие С означает ,что
произошло как событие А ,так и событие
В. Тогда С называют…………………

17. термины 50

Пересечением событий Аи В

18. формулы теории вероятности 10

Классическое
определение
вероятности

19. формулы 10

20. Формулы 20

Оценка вероятности

21. формулы 20

22. формулы 30

Если события несовместны,то
Вероятность их суммы……?

23. Формулы 30

24. Формулы 40

Чему равна вероятность двух
независимых событий?

25. формулы 40

26. Формулы 50

Какие формулы применяют ,если
события А и В –зависимые
,совместные

27. Формулы 50

28. Крылатые фразы 10

29. Крылатые фразы 10

Крылатые фразы
М. Ломоносов
10

30. Крылатые фразы 20

31.

Крылатые фразы
К . Гаус
20

32. Крылатые фразы 30

33. Крылатые фразы 30

Крылатые фразы
А.С. Пушкин
30

34. Крылатые фразы 40

35. Крылатые фразы 40

Крылатые фразы
Л. Эйлер
40

36. Крылатые фразы 50

37. Крылатые фразы 50

Крылатые фразы
Б. Паскаль
,
50

38. Задачи о выборе объектов из набора 10

На клавиатуре телефона 10 цифр ,от 0
до 9 . Какова вероятность того ,что
случайно нажатая цифра будет четной
и больше 5?

39. Задачи о выборе объектов из набора 10

Ответ: 0,2

40. Задачи о выборе объектов из набора 20

Перед началом первого тура чемпионата по
теннису участников разбивают на
игровые пары случайным образом с
помощью жребия . Всего в чемпионате
участвуют 16 теннисистов ,среди
которых 7 участников из России, в том
числе Максим Зайцев. Найдите
вероятность того, что в первом туре
Максим Зайцев будет играть с каким-либо
теннисистом из России

41. Задачи о выборе объектов из набора 20

Задачи о выборе объектов из набора
Ответ: 0,4
20

42. Задачи о выборе объектов из набора 30

Футбольную секцию посещают 33 человека,
среди них два брата – Антон и Дмитрий.
Посещающих секцию случайным образом
делят на три команды по 11 человек в
каждой. Найдите вероятность того , что
Антон и Дмитрий окажутся в одной
команде
?

43. Задачи о выборе объектов из набора 30

44. Задачи о выборе объектов из набора 40

Андрей, Борис, Вадим и Гриша заселяются в
гостиницу в два двухместных номера.
Администратор
гостиницы
случайным
образом распределяет их по номерам. Найдите
вероятность того , что Антон и Борис
окажутся в одной команде .

45. Задачи о выборе объектов из набора 40

46. Задачи о выборе объектов из набора 50

Механические
часы
с
двенадцатичасовым циферблатом в
какой то момент сломались и
перестали
ходить.
Найдите
вероятность того , что часовая
стрелка
застыла
,
достигнув
отметки 11 ,но не дойдя до отметки
2 часа

47. Задачи о выборе объектов из набора 50

Задачи о выборе объектов из набора
Условно циферблат можно разделить на 12
секторов, располагающихся
между отметками соседних чисел . Исходом
будем считать остановка
стрелки в указанном секторе . Указанному
событию благоприятствует
три исхода
Ответ : 0,25
50

48. Задачи о пересечении независимых событий 10

В магазине три продавца ,каждый из них занят с
клиентом с вероятностью 0,4. Найдите
вероятность того, что в случайный момент
времени все три продавца заняты (считайте ,что
клиенты заходят независимо друг от друга )

49. Задачи о пересечении независимых событий 10

0,4*0,4*0,4=0,064
Ответ : 0,064

50. Задачи о пересечении независимых событий 20

В магазине стоят два платежных
автомата . Каждый из них может быть
неисправен
с
вероятностью
0,1
независимо от другого автомата.
Найдите вероятность того, что хотя
бы один автомат исправен.

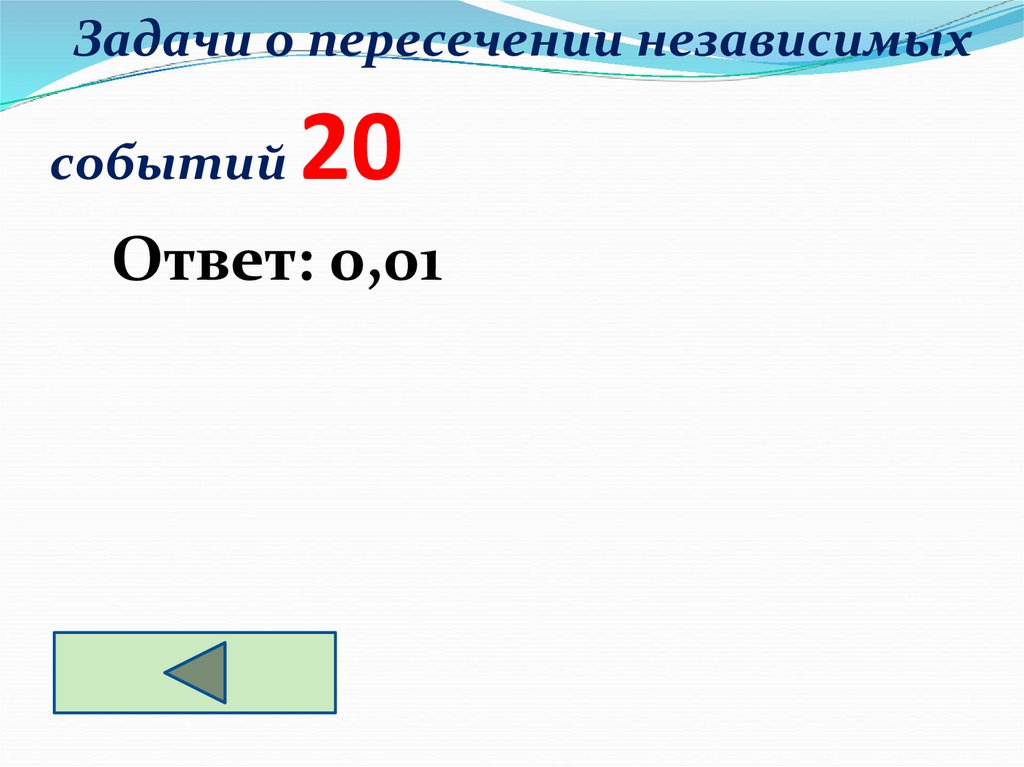
51. Задачи о пересечении независимых событий 20

Ответ: 0,01

52. Задачи о пересечении независимых событий 30

Если гроссмейстер А, играет белыми , то он выигрывает у
гроссмейстера Н , в вероятностью 0,45. если А играет
черными ,то он выигрывает у Н с вероятностью 0,4.
А и Н играют две шахматные партии ,причем во второй
партии меняют цвет фигур . Найдите вероятность
того, что А выиграет оба раза

53. Задачи о пересечении независимых событий 30

Р(А)=0,18

54. Задачи о пересечении независимых событий 40

В классе 16 мальчиков и 9 девочек . Для
подготовки
классной
комнаты
к
занятиям выбирают двух дежурных.
Какова вероятность ,что дежурить
будут две девочки .

55. Задачи о пересечении независимых событий 40

56. Задачи о пересечении независимых событий 50

В урне 9 белых и 7 чёрных шаров.
Из урны вынимаются сразу два шара.
Найти вероятность того, что эти
шары будут разных цветов.

57. Задачи о пересечении независимых событий 50

Событие может появиться в двух
несовместных вариантах: бч и чб. По
теремам сложения и умножения
вероятностей

58. Задачи о противоположном событии 10

При изготовлении подшипников диаметром 55мм
вероятность того ,что диаметр будет отличаться от
заданного не более ,чем на 0,01 мм ,равна 0,925.
Найдите вероятность того ,что случайно
выбранный подшипник будет иметь диаметр
меньше ,чем 54,99 мм,или больше чем 55,01 мм.

59. Задачи о противоположном событии 10

0,075

60. Задачи о противоположном событии 20

В магазине стоят два платежных
автомата.
Оба
могут
быть
неисправны с вероятностью 0,0025.
Найдите вероятность того, что хотя
бы один автомат исправен.

61. Задачи о противоположном событии 20

62. Задачи о противоположном событии 30

В корзине лежат 100 пронумерованных шариков.
Какова вероятность, что не вынут шарик под
номером 6?

63. Задачи о противоположном событии 30

0,99

64. Задачи о противоположном событии 40

В ящике лежат 12 монет,
причем 4 из них фальшивые.
Берут наугад 5 монет. Какова
вероятность,
что
среди
отобранных есть хотя бы одна
фальшивая.

65.

Задачи о противоположном событии
40
Ответ :0.929 События А= {среди отобранных есть хотя бы одна
фальшивая} и событие В = {среди отобранных нет фальшивых
противоположны}. Вычислим только одну вероятность P(В). Общее
количество способов которыми можно извлечь 5 монет из 12 можно
подсчитать легко. Далее считаем
количество способов извлечь 5 нефальшивые (настоящих)
монет из 8 настоящих
Таким образом P(В) = 56/792 = 0,071. и отнимаем от 1

66. Задачи о противоположном событии 50

По отзывам покупателей составлена оценка надежности
двух интернет магазинов .Вероятность того что товар
доставят из магазина А равна 0,85. Вероятность того ,что
товар доставят из магазина В равна 0,96 .найти
вероятность того, что ни один магазин не привезет
заказанный товар в срок .

67. Задачи о противоположном событии 50

Ответ:0,006

68.

69. Финал.

Что
понимают
под
статистической
вероятностью события?
Сформулируйте
закон
больших чисел.

70. Финал.

Если в одинаковых (примерно одинаковых)
условиях проведено достаточно много испытаний,
то за статистическую вероятность события
принимают
относительную
частоту
данного
события либо близкое число.
При статистическом определении в качестве вероятности события
принимается его относительная частота. Таким образом,
статистическая вероятность появления события A в испытаниях
есть отношение числа испытаний, в которых событие A
произошло, к общему числу испытаний.
Закон Бернули: с вероятностью, сколь угодно близкой к единице,
можно утверждать, что при достаточно большом числе
опытов частота появления события А как угодно мало
отличается от его вероятности.

71. Подведение итогов.

72.

рефлексия
Сегодня я узнал --------- Меня удивило -------------- Я задумался ---------------- У меня возник вопрос ---- Я хотел бы ------------------ У меня возникло желание ------------------.