Элементы теории вероятностей

1. Элементы теории вероятностей Пономаренко Н.П.

Презентация
на тему
ЭЛЕМЕНТЫ ТЕОРИИ
ВЕРОЯТНОСТЕЙ
ПОНОМАРЕНКО Н.П.

2. Из истории теории вероятностей

ИЗ ИСТОРИИ ТЕОРИИ ВЕРОЯТНОСТЕЙ

3. ИСПЫТАНИЕ – опыт, эксперимент СОБЫТИЕ – результат испытания: А; В; С; А1; А2… СОВМЕСТНЫЕ СОБЫТИЯ – могут произойти одновременно НЕСОВМЕСТНЫ

ИСПЫТАНИЕ – опыт, эксперимент
СОБЫТИЕ – результат испытания: А; В; С; А1; А2…
СОВМЕСТНЫЕ СОБЫТИЯ – могут произойти одновременно
НЕСОВМЕСТНЫЕ СОБЫТИЯ – не могут произойти
одновременно
ПРОТИВОПОЛОЖНЫЕ СОБЫТИЯ – несовместные, одно из
которых произойдет обязательно:
А - событие, противоположное к А
ДОСТОВЕРНОЕ СОБЫТИЕ Ω – произойдет обязательно
НЕВОЗМОЖНОЕ СОБЫТИЕ – не может произойти

4. Пространство элементарных событий, - совокупность несовместных, равновероятных событий, одно из которых произойдет обязательно

Испытание 1: подбрасывание монеты:
- два элементарных события
ГЕРБ
ЦИФРА
Г
Г
Ц
Ц
Г
Ц
Г
Ц
Испытание 2: подбрасывание двух монет:
- четыре элементарных события
Испытание 3: подбрасывание игральной кости:
- шесть элементарных событий 1 2 3 4 5
Испытание 4: три выстрела в мишень:
- восемь элементарных событий
☻
☻
☻
☻
☻
☻
☻
☻
☻
6
☻
☻
☻

5. ПРОИЗВЕДЕНИЕМ СОБЫТИЙ АВ называется событие, состоящее в том, что оба события А и В происходят СУММОЙ СОБЫТИЙ А + В называется событие, сост

ПРОИЗВЕДЕНИЕМ СОБЫТИЙ АВ называется событие,
состоящее в том, что оба события А и В происходят
СУММОЙ СОБЫТИЙ А + В называется событие, состоящее в
том, что происходит по крайней мере одно из событий А или В
ЗАКОНЫ МОРГАНА:
А В А В - событие, противоположное тому, что произошло
по крайней мере одно из событий, состоит в том, что ни одно из
событий не произошло
АВ А В
- событие. противоположное тому, что произошли
оба события, состоит в том, что по крайней мере одно из событий
не произошло

6. ВОПРОСЫ: Испытание: 5 выстрелов в мишень События: А: « 5 раз попал» В: « по крайней мере один раз попал» Сформулировать события, противоположн

ВОПРОСЫ:
Испытание: 5 выстрелов в мишень
События:
А: « 5 раз попал»
В: « по крайней мере один раз попал»
Сформулировать события, противоположные к А и В
--------------------------------------------------------------------------------------------------------------ВОПРОСЫ:
1) Чему равно произведение несовместных событий?
2) Чему равны произведение и сумма противоположных событий?
3) Чему равны А·А и А + А ?
4) Как записать сумму двух совместных событий в виде суммы трех
несовместных?
-----------------------------------------------------------------------------------------------Аi - событие произошло, Аi - событие не произошло
Сформулируйте смысл формул:
1) А1 А2 А3
2) А1 А2 А3
3) А1 А2 А3
4) А1 А2 А3 А1 А2 А3 А1 А2 А3
5) А1 А2 А3
6) А1 А2 А3

7. Классическое определение вероятности

Событие А БЛАГОПРИЯТСТВУЕТ событию В, если
появление события А влечет появление события В.
т
ВЕРОЯТНОСТЬ события А: Р А п , где m – число
элементарных событий, благоприятствующих событию А, а n –
общее число элементарных событий
-------------------------------------------------------------------------------------
ВОПРОСЫ:
1) Чему равна вероятность достоверного события Р
2) Чему равна вероятность невозможного события Р
3) Какие числовые значения может принимать вероятность любого
события Р (А) ?
--------------------------------------------------------------------------------------------------ЗАДАЧА
В магазин поступило 30 холодильников, 5 из которых имеют заводской
дефект. Случайным образом выбирается один холодильник. Найти
вероятность события А: « холодильник без дефекта»?

8. Задача о четырех котятах ( Мартин Гарднер «А ну-ка догадайся»)

9. Задача о шарах

В урне содержатся 3 белых, 2 желтых и 5 красных шаров.
Испытание: достаем наудачу шар из урны
Найти вероятности событий:
А1: « Белый шар»;
А2: « Желтый шар»;
А3: « Красный шар»;
А4: «Зеленый шар»;
А5: «Красный или желтый шар»;
А6: « Белый, желтый или красный шар»

10. Шахматная задача

ШАХМАТНАЯ ЗАДАЧА
На шахматную доску ставят случайным образом две ладьи, - белую и черную.
Найти вероятность того, что они не побьют друг друга
------------------------------------------------------------------------
На шахматной доске стоит черный слон.
Случайным образом на нее ставят белого слона.
Найти вероятность того,
что они не побьют друг друга.
------------------------------------------------------------------------------------
На шахматной доске стоит черный ферзь.
Случайным образом на нее ставят белого
ферзя. Найти вероятность того, что они не
побьют друг друга.

11. Статистическое определение вероятности

Р А
т
п
Абсолютная частота события А:
где m - количество
появлений события А в n испытаниях
ВЕРОЯТНОСТЬ события А, это число, около которого
группируются значения Р А
при увеличении числа
испытаний

12. Вероятность суммы и произведения событий

Теорема 1:
Для несовместных событий: Р (А + В) = Р (А) + Р (В)
Следствие:
Для противоположного события: Р А 1 Р А
-------------------------------------------------------------------------------------------------------------
Теорема 2:
Для независимых событий: Р (АВ) = Р(А)· Р(В)
-------------------------------------------------------------------------------------------------------------
Теорема 3:
В общем случае:
Р А В 1 Р А В
Следствие: Р А1 Аn 1 P A1 An
то есть вероятность события «произошло по крайней мере одно из событий»
вычисляется по формуле «единица минус вероятность события « ни одно из
событий не произошло»

13. Задача о стрелках

Три стрелка независимо друг относительно друга стреляют в мишень с
вероятностями попадания 0,8; 0,9 и 0,6 соответственно. Найти
вероятности событий:
Е1: « все попали»
Е2: « попал только 2-й»
Е3: « никто не попал»
Е4: « кто-то один не попал»
Е5: « по крайней мере один попал»
Е6: « по крайней мере один промахнулся»
Обозначить Аi событие « i - стрелок попал»

14.

15. № 1 Задача о случайных ответах Требуется ответить на три вопроса теста, каждый из которых содержит 5 вариантов ответа. Найти вероятность сл

№ 1 Задача о случайных ответах
Требуется ответить на три вопроса теста, каждый из которых содержит 5
вариантов ответа. Найти вероятность случайно угадать все три ответа
№2

16.

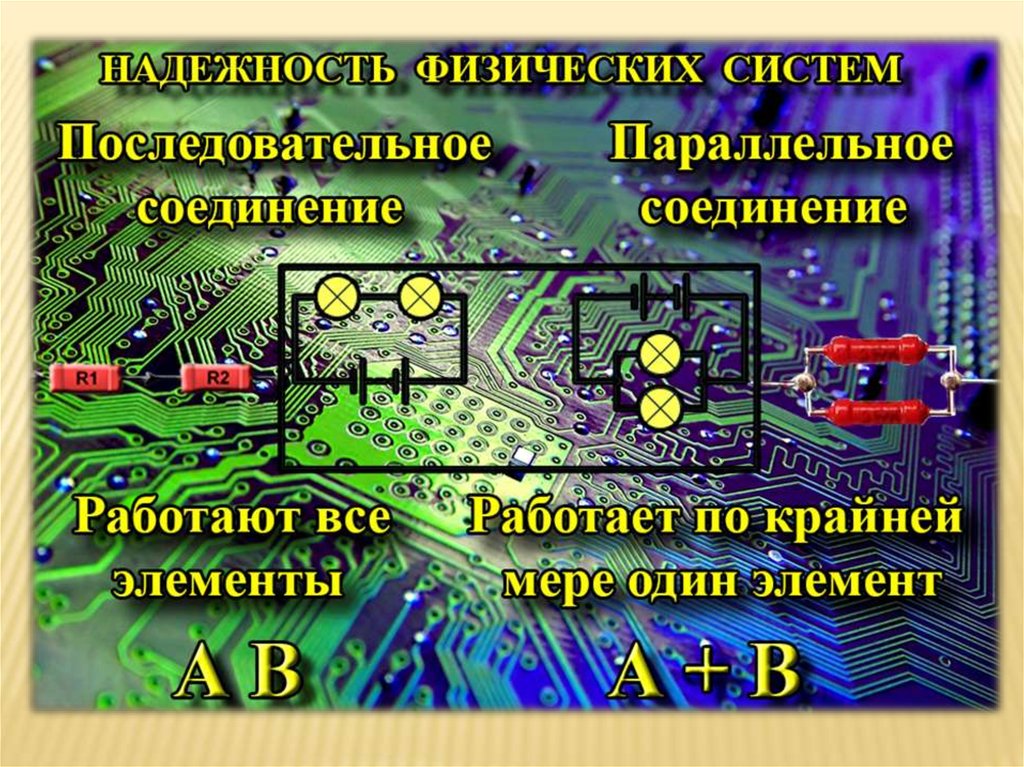
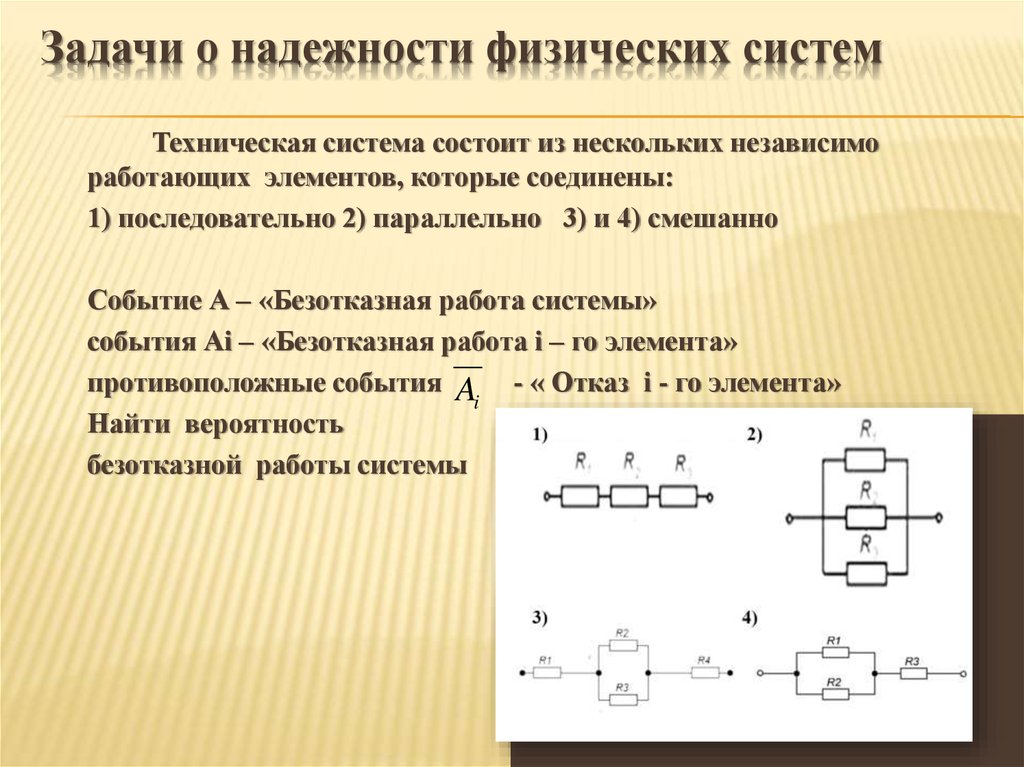
17. Задачи о надежности физических систем

Техническая система состоит из нескольких независимо
работающих элементов, которые соединены:
1) последовательно 2) параллельно 3) и 4) смешанно
Событие А – «Безотказная работа системы»
события Аi – «Безотказная работа i – го элемента»
противоположные события A - « Отказ i - го элемента»
i
Найти вероятность
безотказной работы системы

18. Задача 1 Найти вероятность безотказной работы всех систем, если вероятности безотказной работы всех элементов равны 0,9 ------------------------------------

Задача 1
Найти вероятность безотказной работы всех систем, если
вероятности безотказной работы всех элементов равны 0,9
Р Аi 0,9;
P Ai 0,1;
i 1; 2; 3
------------------------------------------------------------
Задача 2
Найти вероятность безотказной работы
всех систем, если вероятности безотказной
работы всех элементов равны 0,9; 0,8; 0,7
и 0,6 соответственно
Р А1 0,9;
Р А2 0,8;
Р А1 0,1;
Р А2 0,2;
Р А3 0,7;
Р А3 0,3;
Р А4 0,6
Р А4 0,4

19. Задача 1 Техническое устройство содержит два независимо работающих элемента, вероятности отказа которых равны 0,05 и 0, 08 соответственно. Най

Задача 1
Техническое устройство содержит два независимо работающих
элемента, вероятности отказа которых равны 0,05 и 0, 08 соответственно.
Найдите:
1) вероятность нормальной работы устройства ( оба элемента работают)
2) вероятность отказа устройства, для чего достаточно отказа по крайней
мере одного элемента
--------------------------------------------------------------
Задача 2
Вероятность безотказной работы блока, входящего в некоторую
систему в течение заданного времени, равна 0,8. Для повышения
надежности системы устанавливается такой же резервный блок.
Найдите вероятность безотказной работы системы с резервным блоком в
течение заданного времени

20. Задача Техническое устройство состоит из трех независимо работающих элементов. Событие Аi – « i -й элемент исправен» i = 1;2;3 Дано: Р(А1) = 0,6; Р(А2

Задача
Техническое устройство состоит из трех независимо работающих
элементов. Событие Аi – « i -й элемент исправен» i = 1;2;3
Дано: Р(А1) = 0,6; Р(А2) = 0,7; Р(А3) = 0,9
Запишите формулы и
найдите вероятности:
Е1: « все три элемента неисправны»
Е2: « исправен только третий элемент»
Е3: « все три элемента исправны»
Е4: « исправен только один элемент»
Е5: « по крайней мере один элемент исправен»
Е6: « по крайней мере один элемент неисправен»

21. На базе теории вероятностей появилась МАТЕМАТИЧЕСКАЯ СТАТИСТИКА, которую применяют при обработке больших массивов информации и получени

На базе теории вероятностей появилась МАТЕМАТИЧЕСКАЯ
СТАТИСТИКА, которую применяют при обработке больших массивов
информации и получении практически значимых выводов на основании
этого.

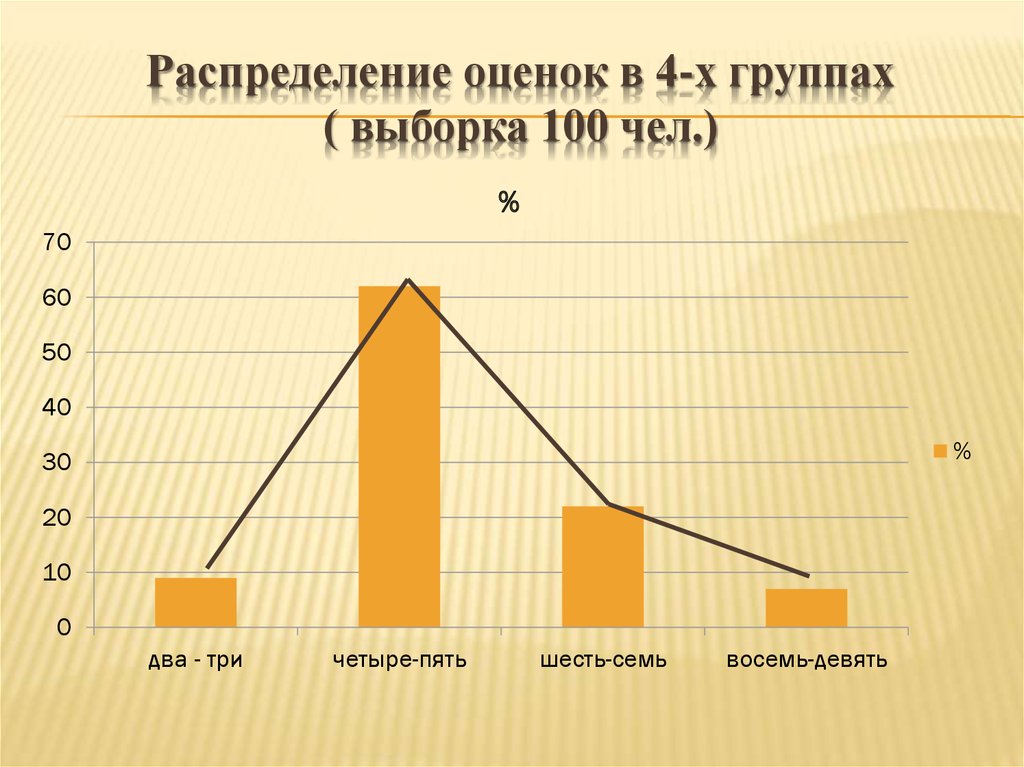
22. Распределение оценок в 4-х группах ( выборка 100 чел.)

%
70
60
50
40
%
30
20
10
0
два - три
четыре-пять
шесть-семь
восемь-девять

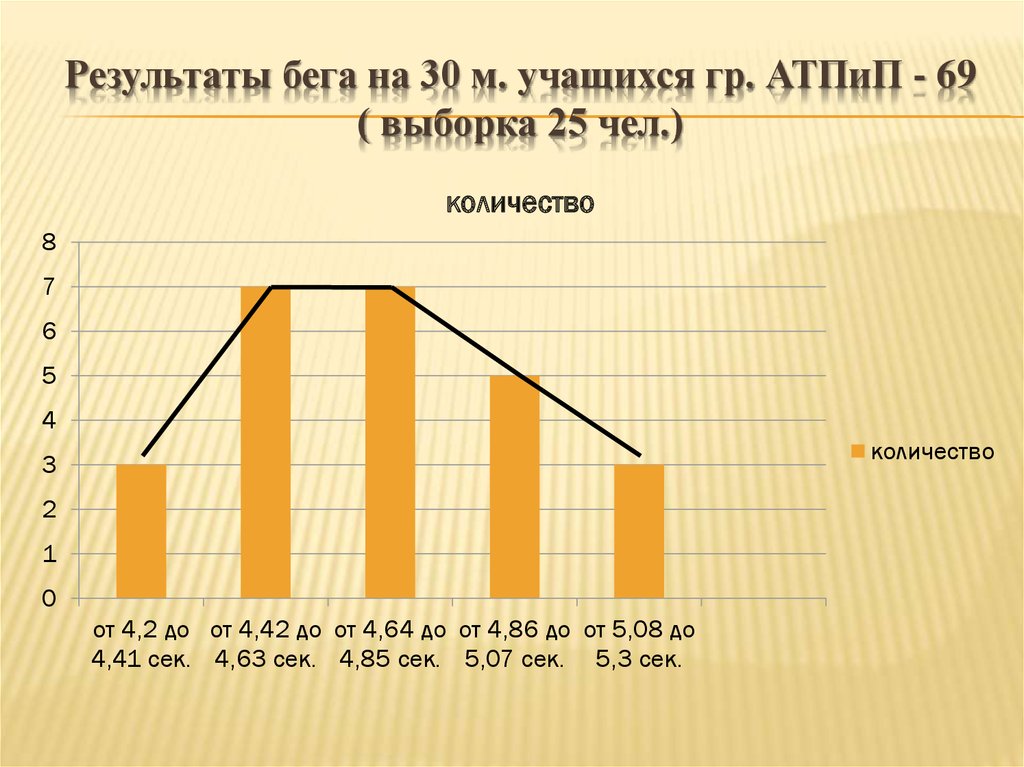
23. Результаты бега на 30 м. учащихся гр. АТПиП - 69 ( выборка 25 чел.)

количество
8
7
6
5
4
количество
3
2
1
0
от 4,2 до от 4,42 до от 4,64 до от 4,86 до от 5,08 до
4,41 сек. 4,63 сек. 4,85 сек. 5,07 сек. 5,3 сек.

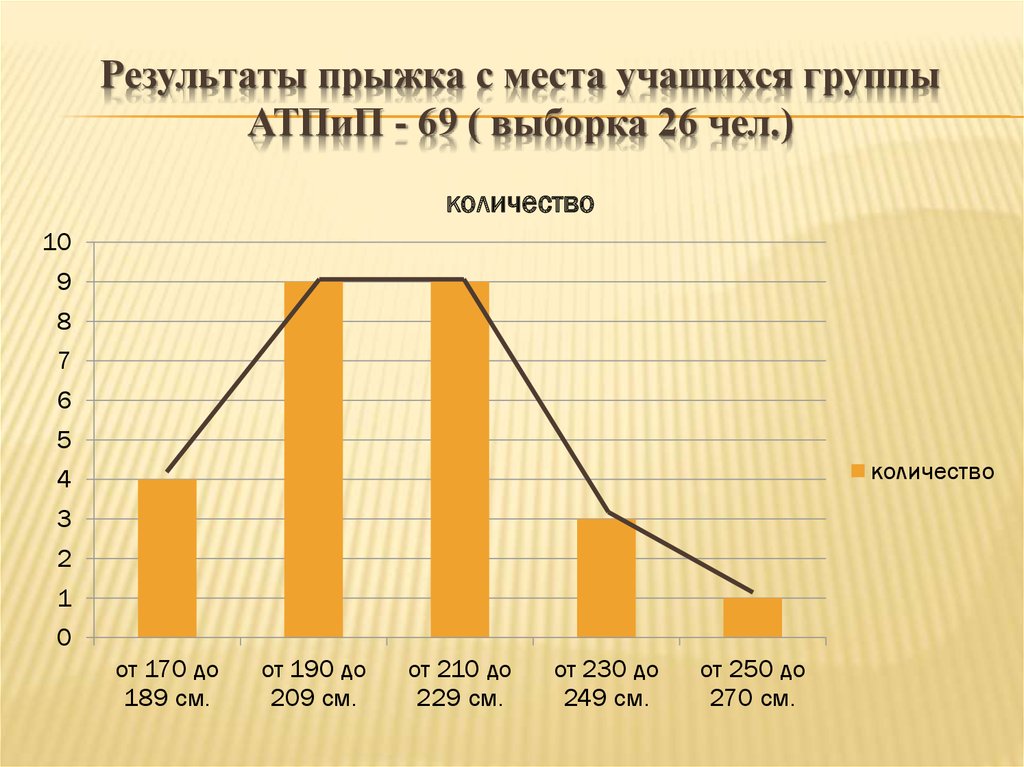
24. Результаты прыжка с места учащихся группы АТПиП - 69 ( выборка 26 чел.)

количество
10
9
8
7
6
5
количество
4
3
2
1
0
от 170 до
189 см.
от 190 до
209 см.
от 210 до
229 см.
от 230 до
249 см.
от 250 до
270 см.