Similar presentations:
IMAD (1)
1. Интеллектуальные методы анализа данных
2. Data Mining
Data Mining – это процесс обнаружения в сырых данных ранее неизвестных,нетривиальных, практически полезных знаний, необходимых для принятия
решений в различных сферах человеческой деятельности.
Особенности:
Данные могут быть неточными, неполными, противоречивыми, и при
этом иметь гигантские объемы.
Алгоритмы анализа данных могут обладать «элементам интеллекта»,
в частности, способностью обучаться по прецедентам, делать общие
выводы на основе частных наблюдений.
Процессы переработки сырых данных в информацию, а информации
в знания уже не могут быть выполнены вручную.
Задачи:
прикладной статистики
машинного обучения
информационного поиска
и т.д.
3. Классификация и кластеризация
Кластеризация — это разделение множества входных векторов на группы(кластеры) по степени «схожести» друг с другом. Внутри каждой группы
должны оказаться «похожие» объекты, а объекты разных групп должны
быть как можно более различны. Число кластеров и правило, в соответствии
с которым объекты разбиваются на классы, изначально не задано и
определяется в процессе работы алгоритма.
Главное отличие классификации от кластеризации состоит в том, что число
классов и решающее правило отнесения объектов к классам заранее
известны.
Цели кластеризации:
Понимание данных – разбиение выборки на группы схожих объектов
позволяет упростить дальнейшую обработку данных и принятия решений,
применяя к каждому кластеру свой метод анализа (стратегия «разделяй и
властвуй»).
Сжатие данных – можно сократить выборку, оставив по одному
наиболее типичному представителю от каждого кластера.
Обнаружение новизны – выделяются нетипичные объекты, которые не
удаётся присоединить ни к одному из кластеров.
4. Этапы кластеризации
1. Отбор выборки объектов для кластеризации.2. Определение множества переменных, по которым
будут оцениваться объекты в выборке. При
необходимости – нормализация значений переменных.
3. Вычисление значений меры сходства между объектами.
4. Применение метода кластерного анализа для создания
групп сходных объектов (кластеров).
5. Представление результатов анализа.
После получения и анализа результатов возможна корректировка
выбранной метрики и метода кластеризации до получения
оптимального результата.
5. Методы кластеризации
Вероятностный подход: K-средних (K-means), K-medians, EM-алгоритм,Алгоритмы семейства FOREL, Дискриминантный анализ, …
Подходы на основе систем искусственного интеллекта: Метод нечеткой
кластеризации C-средних (C-means), Нейронная сеть Кохонена, Генетический
алгоритм, …
Логический подход: Построение
помощью дерева решений.
дендрограммы
с
Теоретико-графовый подход: Графовые алгоритмы кластеризации.
Иерархический подход: Предполагается наличие вложенных групп.
Алгоритмы в свою очередь подразделяются на агломеративные
(объединительные) и дивизивные (разделяющие).
Другие методы: Статистические алгоритмы кластеризации, Ансамбль
кластеризаторов, Алгоритмы семейства KRAB, Алгоритм, основанный на
методе просеивания, DBSCAN и др.
6. Формальная постановка задачи кластеризации
Пусть — множество объектов, — множество номеров (имён, меток)кластеров. Задана функция расстояния между объектами
. Имеется
конечная обучающая выборка объектов
. Требуется
разбить
выборку
на
непересекающиеся
подмножества,
называемые кластерами, так, чтобы каждый кластер состоял из объектов,
близких по метрике , а объекты разных кластеров существенно
отличались. При этом каждому объекту
приписывается номер
кластера .
Алгоритм кластеризации — это функция
, которая любому
объекту
ставит в соответствие номер кластера
.
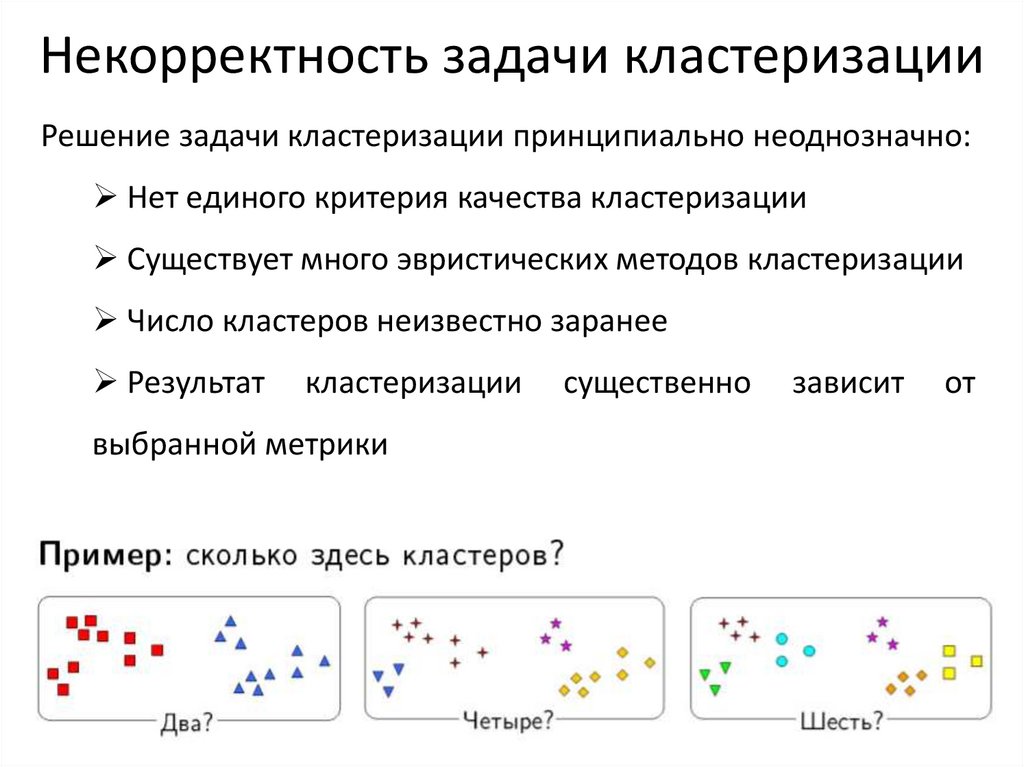
7. Некорректность задачи кластеризации
Решение задачи кластеризации принципиально неоднозначно:Нет единого критерия качества кластеризации
Существует много эвристических методов кластеризации
Число кластеров неизвестно заранее
Результат
кластеризации
выбранной метрики
существенно
зависит
от
8. Расстояние между объектами
Метрика – это функция, которая каждой паре векторов ставитв соответствие неотрицательное число, называемое
расстоянием.
Для количественной шкалы:
n
D x, w
xi wi
2
– Евклидово расстояние
i 1
n
D x, w xi wi
i 1
D x, w x, w
– Мера Манхэттена
(расстояние городских кварталов)
– Скалярное произведение
9. Расстояние между объектами
Для шкалы наименований (категорий):1 n
0 | xi wi
D x, w di , где di
n i 1
1 | xi wi
Для смешанных признаков (когда имеется
категориальных признаков и n−L количественных):
n
2 min xi , wi
L
1
D x, w di n L 1 i nL 1
n
n i 1
xi wi
l L 1
l L 1
L
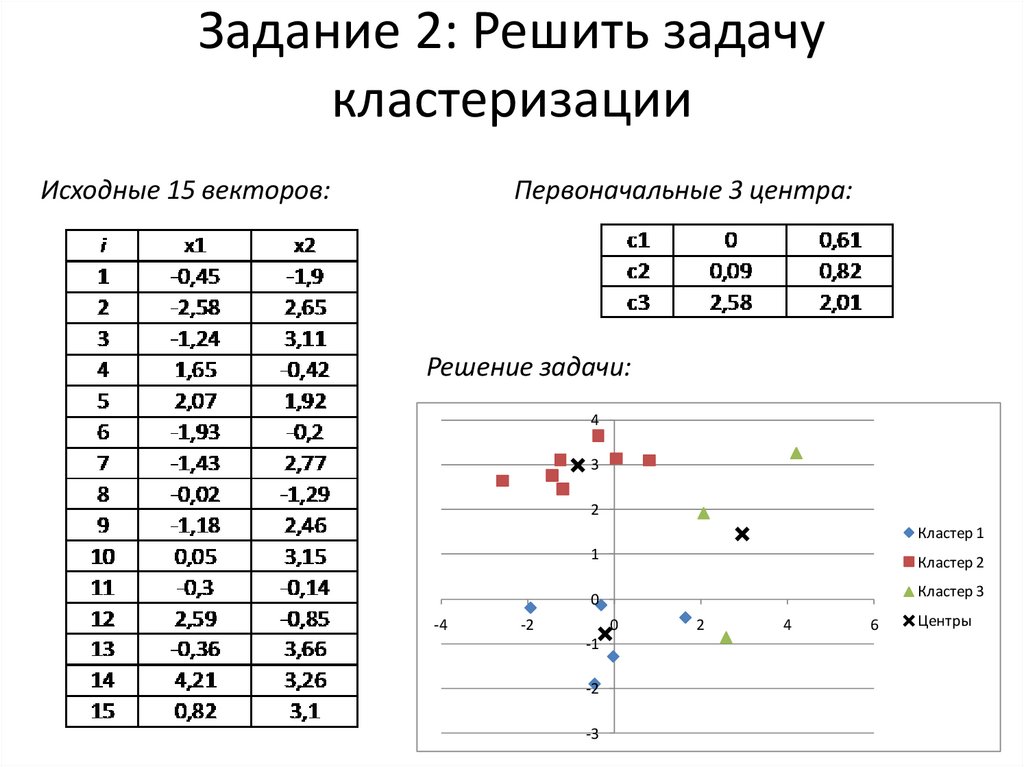
10. Задание 1: вычислить расстояния между объектами
1. Найти расстояния Евклида, Манхэттена, скалярное для парывекторов x1 и y1:
x1 = (6, 2, 2, 3, 1, 3, 3, 5, 6)
y1 = (6, 8, 7, 3, 6, 7, 2, 7, 1)
2. Найти расстояние в шкале наименований для пары векторов x2
и y2:
x2 = (b, b, a, b, a, b, a, a, b, c)
y2 = (c, c d, b, a, c, c, b, d, d)
3. Найти расстояние в смешанной шкале для пары векторов x3 и
y3:
x3 = (a, b, d, a, a, 3, 1, 4, 6, 7)
y3 = (b, d, d, a, d, 1, 6, 5, 3, 6)
11. Нормализация данных
В процессе нормализации все значения приводятся кнекоторому диапазону, например, [-1, -1] или [0, 1].
~
x q , q 1, p
– исходные данные
q
min
~
x
x
i
i
xiq max
xi ximin
– безразмерные данные
xiq
q
xi
n
i 1
q 2
xi
– нормализованные данные
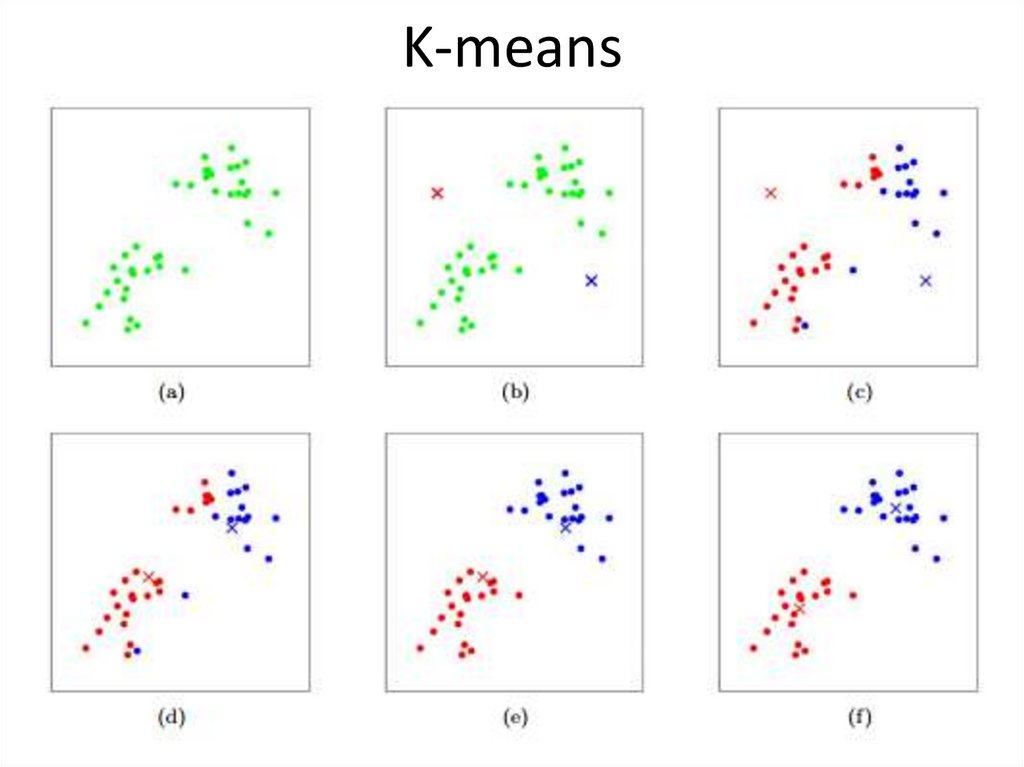
12. K-means
Разбивает множество элементов векторного пространства на заранее известноечисло кластеров K. Алгоритм стремится минимизировать среднеквадратичное
отклонение на точках каждого кластера. На каждой итерации перевычисляется центр
масс для каждого кластера, полученного на предыдущем шаге, затем векторы
разбиваются на кластеры вновь в соответствии с тем, какой из новых центров
оказался ближе по выбранной метрике. Алгоритм завершается, когда на какой-то
итерации не происходит изменения кластеров.
1. Пусть заданы центры кластеров: c ci , i 1, n; k 1, K
k
k
2. Для каждого кластера из элементов обучающей выборки определяется
множество ближайших объектов:
J k j | min D x j , c k , j 1, p
k
3. После чего, происходит уточнение центров кластеров по следующей
формуле:
1
k
j
c (t )
J
k
x , t 1,2,3,...
j J k
4. Итерации останавливаются, когда не происходит дальнейшего изменения
кластеров, т.е. выполняется условие:
ck (t ) ck (t 1)
13. K-means
14. Недостатки метода K-means
необходимо заранее знать количество кластеров.алгоритм очень чувствителен к выбору начальных центров
кластеров. Классический вариант подразумевает случайный
выбор кластеров, что очень часто являлось источником
погрешности.
не справляется с задачей, когда объект принадлежит к
разным кластерам в равной степени или не принадлежит ни
одному.
15. Метод нечеткой самоорганизации C-means
Вместо однозначного ответа на вопрос, к какому кластеруотносится объект, метод С-means определяет с какой степенью
объект принадлежит к тому или иному кластеру.






















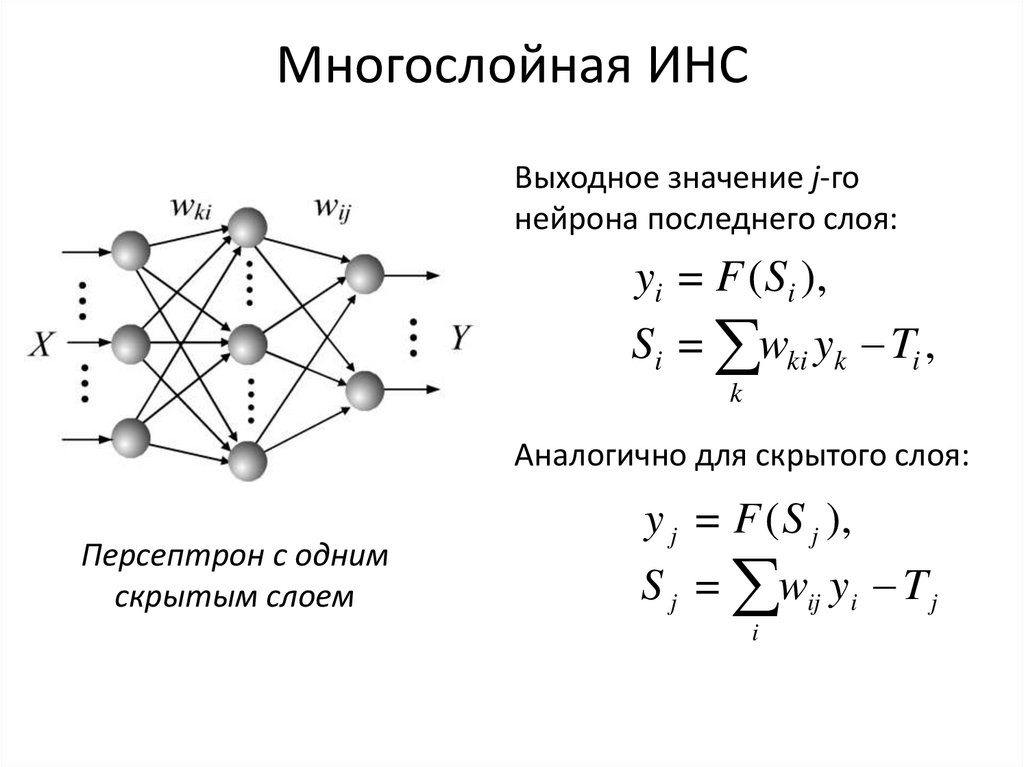

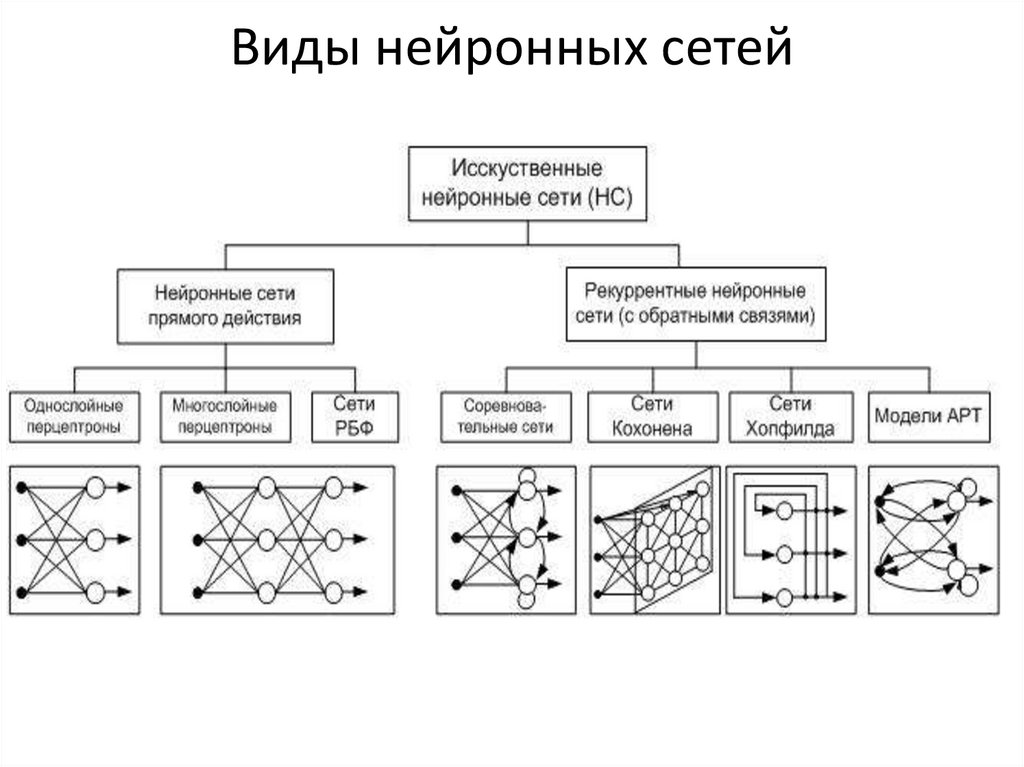


 informatics
informatics








