3.97M

Нахождение аналогов

1.

Нахождение аналогов
Профессор Кузнецов Анатолий Дмитриевич
Доцент Восканян Карина Левановна
Доцент Сероухова Ольга Станиславовна
Учебная дисциплина
«Текущее прогнозирование»
2019

Нахождение двух аналогичных отрезков внутри
заданного временного ряда — это один из возможных методов его
исследования, которое возможно прежде всего тогда, когда в
рассматриваемом временном процессе, описываемом временным
рядом, существуют аналогии между реализациями процесса в
разные отрезки времени.

3.

При использовании метода аналогий известные в прошлом
приемы и методы привлекаются для анализа исходных ситуаций,
встречающихся в настоящее время.
Метод аналогов: поиск в обучающей выборке объектов –
аналогов
заданному
объекту
на
основе
использования
количественных или качественных характеристики их «близости».
Иными словами метод аналогов заключается в поиске в
предыстории временного ряда заданной длины n среди всех
векторов размерности l, составленных из всех возможных наборов
отрезков этого временного ряда (fi, fi+1, . . . , fi+l−1), одного или
нескольких векторов, наиболее «похожих» на последний в
рассматриваемой выборке вектор (fn−l+1, fn−l+2, . . . , fn).
При этом мера сходства («похожести», «адекватности»)
определяется с помощью задания соответствующей метрики.

4.

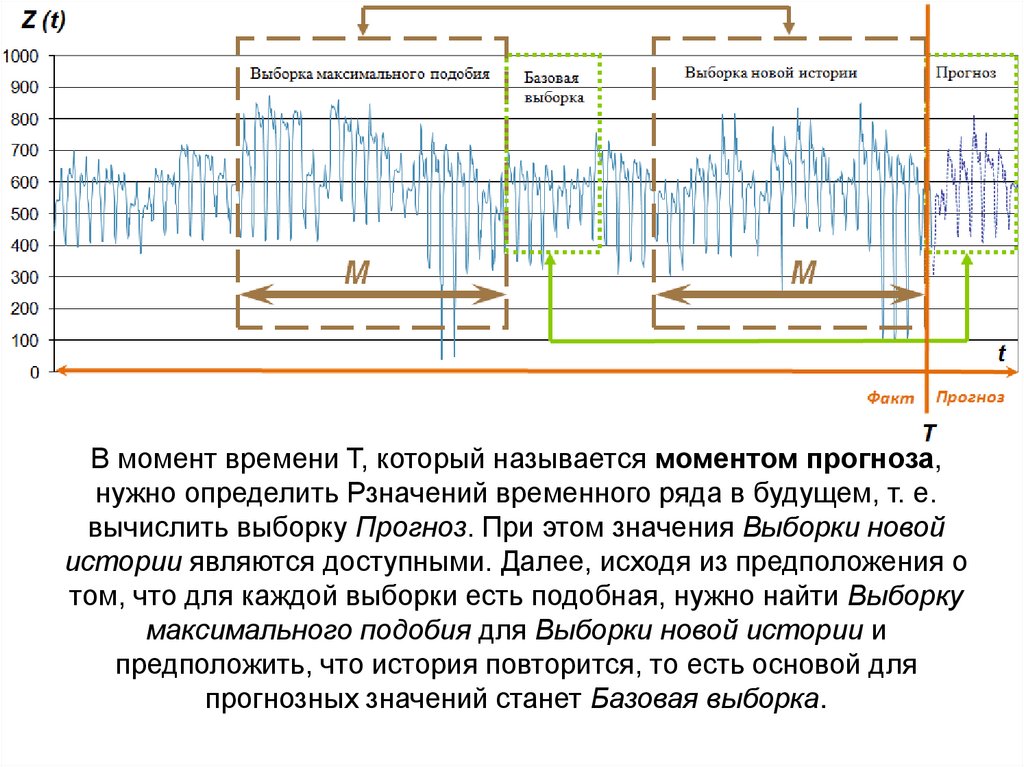
В момент времени T, который называется моментом прогноза,
нужно определить Pзначений временного ряда в будущем, т. е.
вычислить выборку Прогноз. При этом значения Выборки новой
истории являются доступными. Далее, исходя из предположения о
том, что для каждой выборки есть подобная, нужно найти Выборку
максимального подобия для Выборки новой истории и
предположить, что история повторится, то есть основой для
прогнозных значений станет Базовая выборка.

5.

Тестируемаяв выборка n1-1
1
n1
n2
Время
1)
Δ=n2-n1+1
1
2)
2
Эталонный
отрезок
Δ=n2-n1+2
3)
3
Δ=n2-n1+3
Тестируемые отрезки
(черные),
Длина отрезка
временного ряда,
для которого
ищется аналог
аналог (синий),
ТП (коричневый)
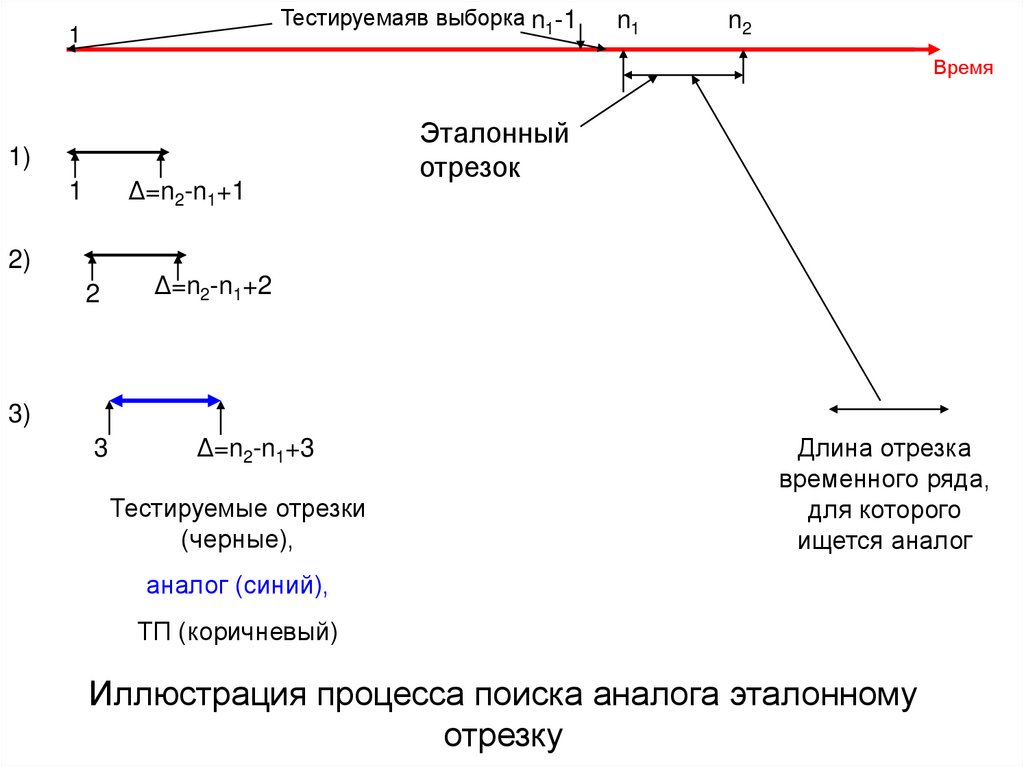
Иллюстрация процесса поиска аналога эталонному
отрезку

6.

То есть при использовании метода аналогов необходимо
подобрать из всех заданной продолжительности отрезков прошлых
значений временного ряда близкие к эталонному отрезку.

7.

Практические эксперименты показали, что успешность
процесса поиска аналогаэффективность прогноза зависит главным
образом от следующих основных факторов:
- длины используемой предыстории - «памяти» ряда;
- выбора критерия оценки близости аналогов к искомому эталону;
- того, имеются ли в истории ряда похожие случаи.

8.

Метрики

9.

Для определения меры сходства двух объектов временного
ряда (метрики) наиболее широкое распространение получили
меры расстояния.
Наиболее привычной мерой расстояния представляется
геометрическое расстояние между двумя точками на плоскости.
Если известны декартовы координаты этих точек: (x1,y1) и (x2,y2), то
геометрическое расстояние равно:
L ( x1 x2 ) 2 ( y1 y 2 ) 2
Однако понятие взаимного расстояния (взаимной меры
сходства) можно обобщить не только на такие объекты как
совокупность точек в пространстве. При таком обобщении в
качестве меры расстояния между объектами служат метрики,
которые позволяют количественно описать степень сходства
объектов самой разной природы.

10.

Выбор метрики, определяющей меру сходства двух
объектов временного ряда, полностью лежит на
исследователе, поскольку результаты кластеризации
могут существенно отличаться при использовании
разных метрик.
Поэтому для достижения наилучшего результата
необходимо экспериментировать с выбором мер
расстояний (метрик), а также менять алгоритм (метод
кластеризации).
Никакого единого решения не существует!

11.

Меры сходства двух отрезков временного ряда одинаковой
длины (метрики) можно подразделить на четыре вида:
- коэффициенты корреляции;
- меры расстояния;
- коэффициенты ассоциативности;
- вероятностные коэффициенты сходства.
Наиболее широкое распространение получили меры
расстояния и коэффициенты корреляции, поэтому в данной работе
рассматриваются именно они.
Если два отрезка временного ряда идентичны, то все
соответствующие значения в этих отрезках принимают одинаковые
значения. В этом случае расстояние между ними равно нулю, а
коэффициент корреляции равен 1.

12.

Рассмотрим наиболее известные методы оценки расстояния
между отрезками временного ряда (метрики), заданными векторами
x и y, и методику их применения при реализации метода аналогов.
При рассмотрении метрик будем считать, что оценивается
близость
двух отрезков временного ряда, заданных векторами
(аналог) и y (эталон):
x1
x2
...
xn
y1
y2
...
yn
x

13.

1. Стандартная Евклидова метрика:
Ev (x, y ) (x y ) (x y )
Т
или
Е ( x, y, n )
n
2
x
y
i i
(1)
i 1
где х и у – значения временного ряда, исследуемого на
принадлежность к аналогу отрезка и контрольного отрезка-эталона
соответственно;
n – длина векторов х и у – аналога и эталона.
Тот отрезок х, для которого значение сумма квадратических
отклонений окажется минимальным, принимается за аналог
контрольному отрезку временного ряда у.

14.

2. Квадрат Евклидова расстояния, когда возведение
в
квадрат стандартного Евклидова расстояния придает большие веса
более отдаленным друг от друга значениям:
Ev (x, y ) (x y ) (x y )
Т
n
или
Е (x, y, n ) xi yi 2
i 1
(2)

15.

3. Манхеттенское расстояние, или «расстояние городских
кварталов» (city-block) определяется следующим образом:
n
м ( x , y , n ) xi y i
i 1
(3)
Манхэттенское расстояние позволяет уменьшать влияние
отдельных больших выбросов.

16.

4. Относительное расстояние, при котором метрика
определяется
относительной разностью совпадения двух
векторов (двух отрезков временного ряда):
1 n xi y i
( x, y , n )
q i 1 xi y i
(4)

17.

5. Расстояние Чебышева:
ch (x, y, n) max ( xi yi ), i 1... n
(5)

18.

6.
Коэффициент
корреляции,
определяющий
степень
взаимного влияния двух отрезков временного ряда:
n
(x x) ( y y)
i
r ( x, y, n )
i
i 1
n
2
(
x
x
)
i
i 1
n
2
(
y
y
)
i
i 1
(6)

19.

Следующие метрики содержат эмпирические параметры,
позволяющие придать их использованию более универсальный
подход к определению степени близости векторов, однако
задание таких параметров является не тривиальной задачей.
7. Степенное расстояние, где r и p — параметры, определяемые
пользователем:
n
c ( x , y , n, p, r ) ( xi y i )
p
1/ r
(7)
i 1
Данная метрика позволяет прогрессивно увеличить или
уменьшить вес, относящийся к размерности, для которой
соответствующие значения сильно отличаются. Параметр p
ответственен за постепенное взвешивание разностей по
отдельным координатам, параметр r - за прогрессивное
взвешивание больших расстояний между объектами. Если оба
параметра: r и p, равны двум, то это расстояние совпадает с
расстоянием Евклида.

20.

8. Метрика Минковского:
p
M ( x , y , n, p ) xi y i
i 1
n
1/ p
(8)

21.

В рассмотренных ранее схемах сравнения отрезков временного
ряда предполагалась равноценность элементов отрезков с точки
зрения определения их близости и, тем самым, их равноценность
для последующего прогностического отрезка. В этом случае
алгоритмы сравнения упрощаются.
Однако такое уравнивание не учитывает уменьшение ценности в
нем элементов, содержащихся в эталонном отрезке, по мере
удаления от его «правого» края, т. е. по мере удаления от
последнего (до начала текущего прогноза) имеющегося во
временном ряду элемента.
Частично этот недостаток устраняется при использовании
следующей метрики, предполагающей введение весовых
коэффициентов для элементов, сравниваемых между собой
векторов.

22.

9. Диагонально взвешенная Евклидова метрика:
EvW (x, y ) (x y ) Λ (x y )
Т
(9)
где матрица Λ = diag(λ).
Для диагональной матрицы последнее соотношение можно
записать в следующем виде:
Е W ( x, y, n, ii )
n
2
xi y i
i 1
ii
(10)

23.

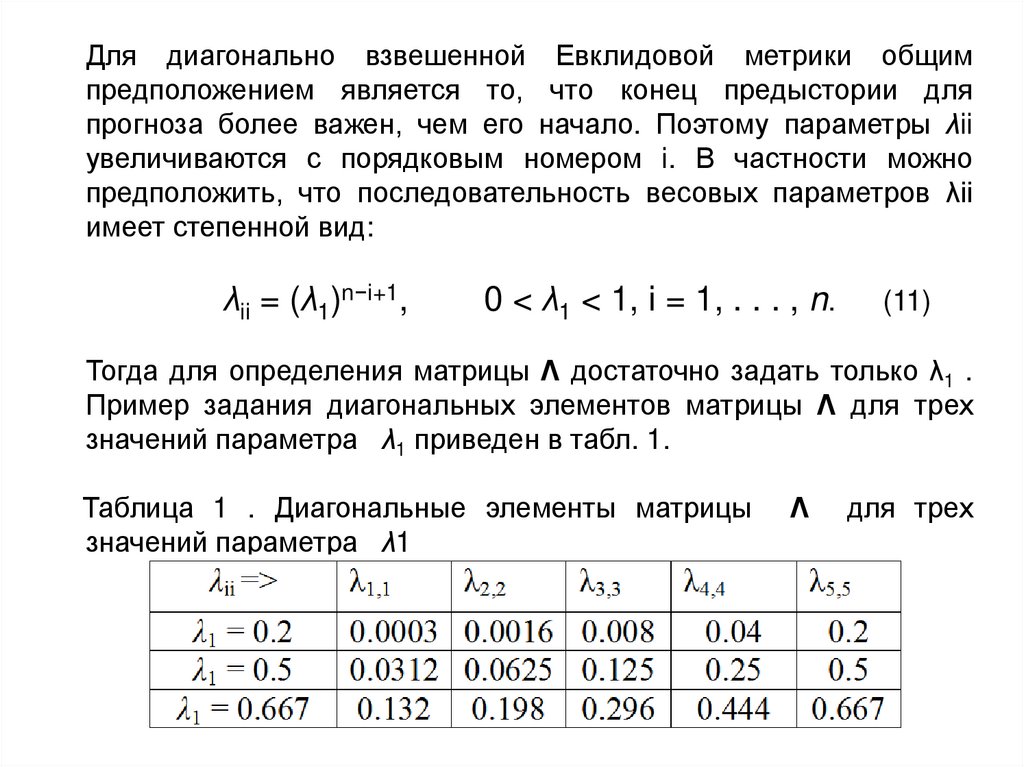
Для диагонально взвешенной Евклидовой метрики общим
предположением является то, что конец предыстории для
прогноза более важен, чем его начало. Поэтому параметры λii
увеличиваются с порядковым номером i. В частности можно
предположить, что последовательность весовых параметров λii
имеет степенной вид:
λii = (λ1)n−i+1,
0 < λ1 < 1, i = 1, . . . , n.
(11)
Тогда для определения матрицы Λ достаточно задать только λ1 .
Пример задания диагональных элементов матрицы Λ для трех
значений параметра λ1 приведен в табл. 1.
Таблица 1 . Диагональные элементы матрицы
значений параметра λ1
Λ
для трех

24.

Рассмотренный вариант задания диагональных элементов
матрицы Λ не связан со свойствами имеющейся выборки
временного ряда и подразумевает эвристический подбор этих
параметров.
Следовательно, такой подход к определению метрики
оставляет неопределенность в задании параметров матрицы Λ.
Эту
неопределенность
в
реализации
расчетов
с
использованием диагонально взвешенной Евклидовой метрики
можно преодолеть, определив оптимальное значение параметра
λ1 на основе проведения серии численных экспериментов на
имеющемся архиве экспериментальных данных.

25.

10. Расстояние
следующий вид:
Махаланобиса,
формула
( x, y ) ( x y ) Σ
Т
где
1
которого
(x y )
имеет
(12)
Σ - общая внутригрупповая дисперсионно-ковариационная
матрица.
В отличие от метрик Минковского и Евклидовой, эта метрика
связана с корреляциями переменных, задаваемых с помощью
матрицы дисперсий-ковариаций.

26.

2. Стандартная Евклидова метрика:
Е ( x, y, n )
n
2
x
y
i i
i 1
6. Диагонально взвешенная Евклидова метрика:
Е W ( x, y, n, ii )
n
2
x
y
i
i
i 1
λii = λ11n−i+1,
ii
0 < λii < 1, i = 1, . . . , n.
n
м ( x , y , n ) xi y i
1. Манхэттенское расстояние:
i 1
n
p
M и ( x , y , n, p ) x i y i
i 1
3. Метрика Минковского порядка p: ρМи
4. Относительное расстояние между двумя векторами: ρо
1 n xi y i
o ( x, y , n )
n i 1 xi y i
5. Коэффициент корреляции
n
r ( x, y , n )
( x x ) ( y y)
i
i 1
i
n
n
( x x ) ( y y)
2
i
i 1
i
i 1
2
1/ p

27.

Программа
«Аналоги2019.xls»

28.

Входными параметрами программы «Аналоги2019.xls»
являются:
1. Номер колонки, в которой на Листе 1 содержится исследуемый
временной ряд: nk.
2. Общая длина иследуемого временного ряда: nn.
3. Число искомых аналогов: na.
4. Начальный номер отрезка, для которого будет искаться аналог :
n1.
5.Конечный номер отрезка, для которого будет искаться аналог : n2.
6.Начальное значение матрицы в диагонально взвешенной метрики
λ1 : lamd.
7.Порядок метрики Минковского – параметр p: pmin.

29.

Информация об используемых метриках на Листах 1 - 5

30.

Информация об используемых метриках на Листах 1 - 5

31.

Программа позволяет после ввода всех входных параметров
произвести нахождение 4 «оптимальных» отрезков временного ряда
(одного оптимального с лучшим значением метрики) и трех
дополнительных «квазиоптимальных» (по мере ухудшения значений
метрики) внутри представленного временного ряда.
Методика последовательного нахождения каждого из трех
«квазиоптимальных» отрезков для данной метрики заключается в том,
что уже ранее найденные отрезки принудительно исключаются из
рассмотрения как оптимальные.

32.

Результаты расчетов сгруппированы на Лист2 – Лист5 и Листе8
по следующей схеме (для na = 4):
1. На Лист2 – значения оптимального отрезка x1, найденного по 6
метрикам для его нахождения.
2. На Лист3 – то же, что и Лист 2, но для первого квазиоптимального
аналога, найденного по 6 метрикам для его нахождения: x2*.
3. На Лист4 – то же, что и Лист 2, но для второго квазиоптимального
аналога, найденного по 6 метрикам для его нахождения: x3*.
4. На Лист5 – то же, что и Лист 2, но для третьего
квазиоптимального аналога, найденного по 6 метрикам для его
нахождения: x4*.

33.

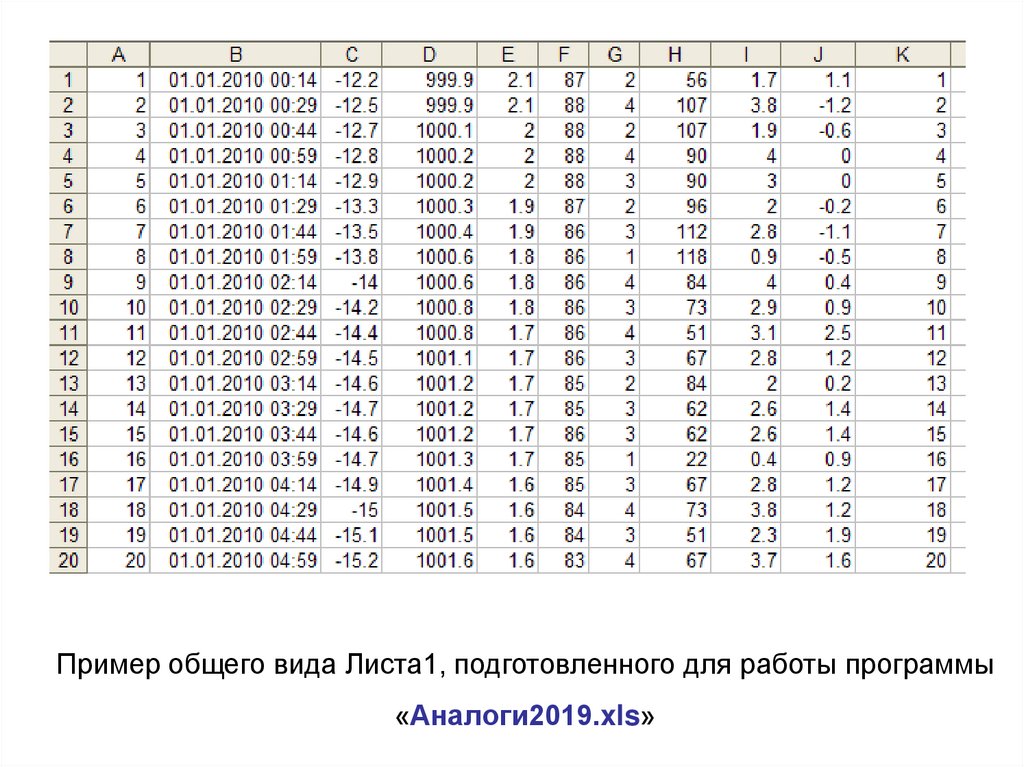
На следующем слайде представлен фрагмент исходных
для проведения расчетов данных на Листе 1, полученных с
помощью АМС с дискретностью 15 мин, которые в дальнейшем
использовался для иллюстрации работы программы «Поиск
всех аналогов.xls»: колонка «С» - температура воздуха, 0С.

34.

Пример общего вида Листа1, подготовленного для работы программы
«Аналоги2019.xls»

35.

После работы программы «Аналоги2019.xls» на Листе2
приводятся данные как для оптимальных отрезков, найденных с
использованием 6 метрик, так и результаты прогноза, полученного с
использованием 7 подходов к его построению.
Всего таких фрагментов на Листе2 шесть, соответствующих
шести методикам нахождения оптимального отрезка и построения
прогноза:
1. Манхэттенское расстояние
2. Евклидова метрика
3. Минковского метрика.
4. Минимум суммы относительной абсолютной разности двух
отрезков.
5. Максимум коэффициента корреляции двух отрезков.
6. Диагонально взвешенная Евклидова метрика.

36.

На следующем слайде в качестве примера для
метрики №1 (Манхеттенское расстояние) представлен общий
вид одного из шести имеющихся на Листе2 фрагментов
представления результатов расчетов.

37.

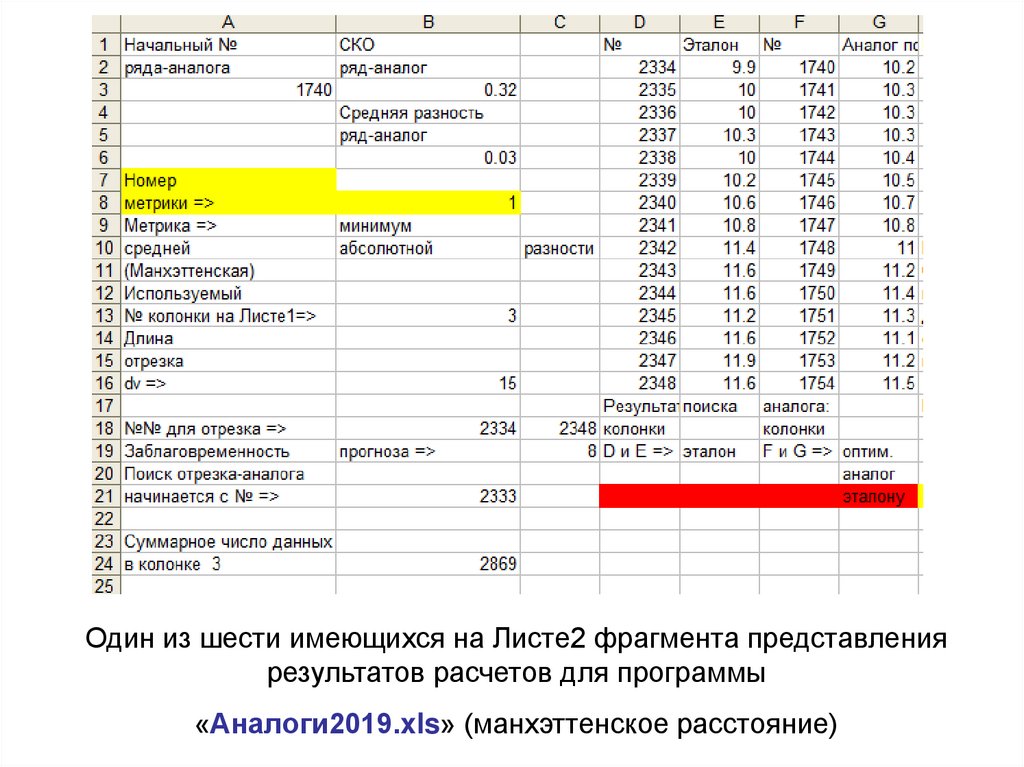
Один из шести имеющихся на Листе2 фрагмента представления
результатов расчетов для программы
«Аналоги2019.xls» (манхэттенское расстояние)

38.

Фрагменты Листа2,
на котором представлена информация о
результатах нахождения оптимальных (с
точки зрения используемой метрики)
отрезков временного ряда, являющимися
наиболее «близким» эталонному отрезку

39.

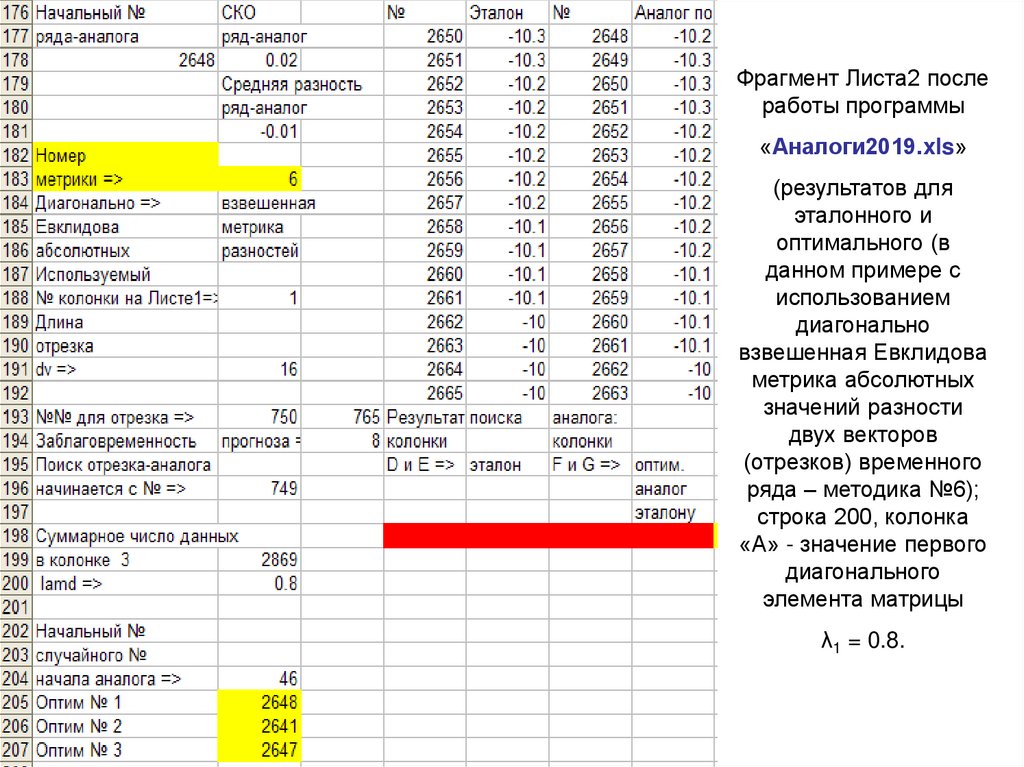
Фрагмент Листа2 после
работы программы
«Аналоги2019.xls»
(результатов для
эталонного и
оптимального (в
данном примере с
использованием
диагонально
взвешенная Евклидова
метрика абсолютных
значений разности
двух векторов
(отрезков) временного
ряда – методика №6);
строка 200, колонка
«А» - значение первого
диагонального
элемента матрицы
λ1 = 0.8.

40.

На следующем слайде приведен фрагмент Листа2, где
представлена следующая информация:
- начальном элементе оптимального аналога;
- статхарактеристики близости эталонного ряда и рядааналога;
- номер используемой метрики;
- номер колонки на Листе1, с которого считывалась
информация о временном ряде;
- длина эталонного отрезка (в единицах дискретности
временного ряда).

41.

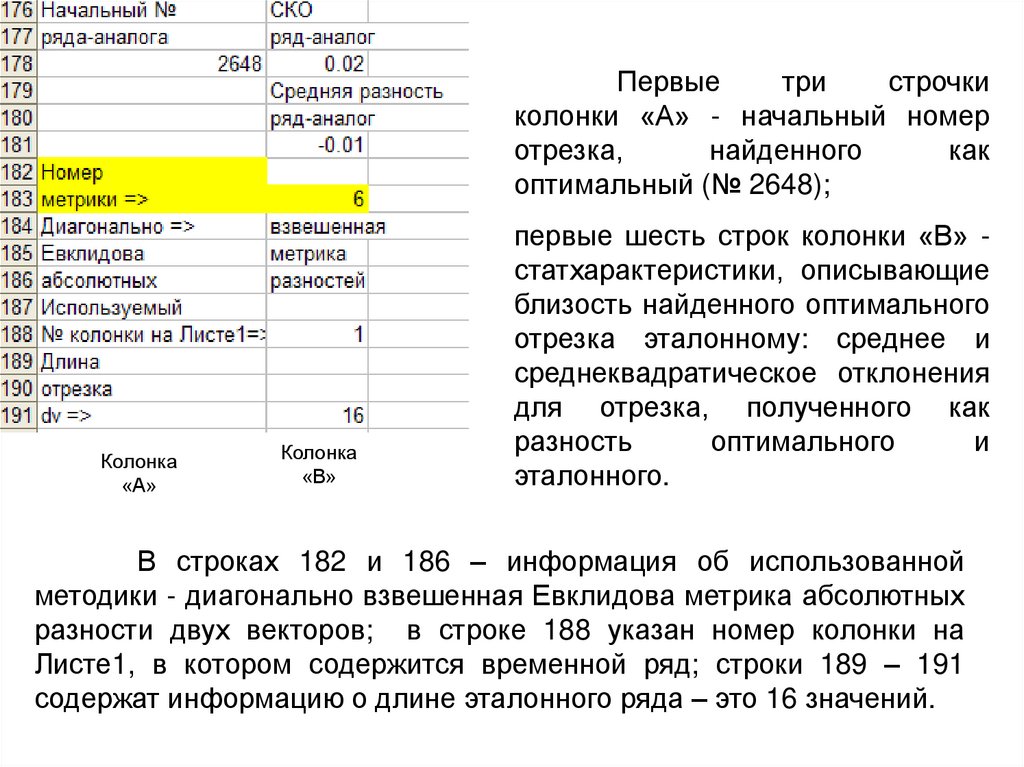
Первые
три
строчки
колонки «А» - начальный номер
отрезка,
найденного
как
оптимальный (№ 2648);
Колонка
«А»
Колонка
«В»
первые шесть строк колонки «В» статхарактеристики, описывающие
близость найденного оптимального
отрезка эталонному: среднее и
среднеквадратическое отклонения
для отрезка, полученного как
разность
оптимального
и
эталонного.
В строках 182 и 186 – информация об использованной
методики - диагонально взвешенная Евклидова метрика абсолютных
разности двух векторов; в строке 188 указан номер колонки на
Листе1, в котором содержится временной ряд; строки 189 – 191
содержат информацию о длине эталонного ряда – это 16 значений.

42.

На
указаны:
следующем слайде показан фрагмент Листа2, где
информация о положении эталонного отрезка (№№
начала и конца),
- суммарное число данных в используемой колонке на
Листе1;
- значение λ1 в диагонально взвешенной Евклидовой
метрике;
- начальные номера оптимального и двух квазиоптимальных
отрезков-аналогов.

43.

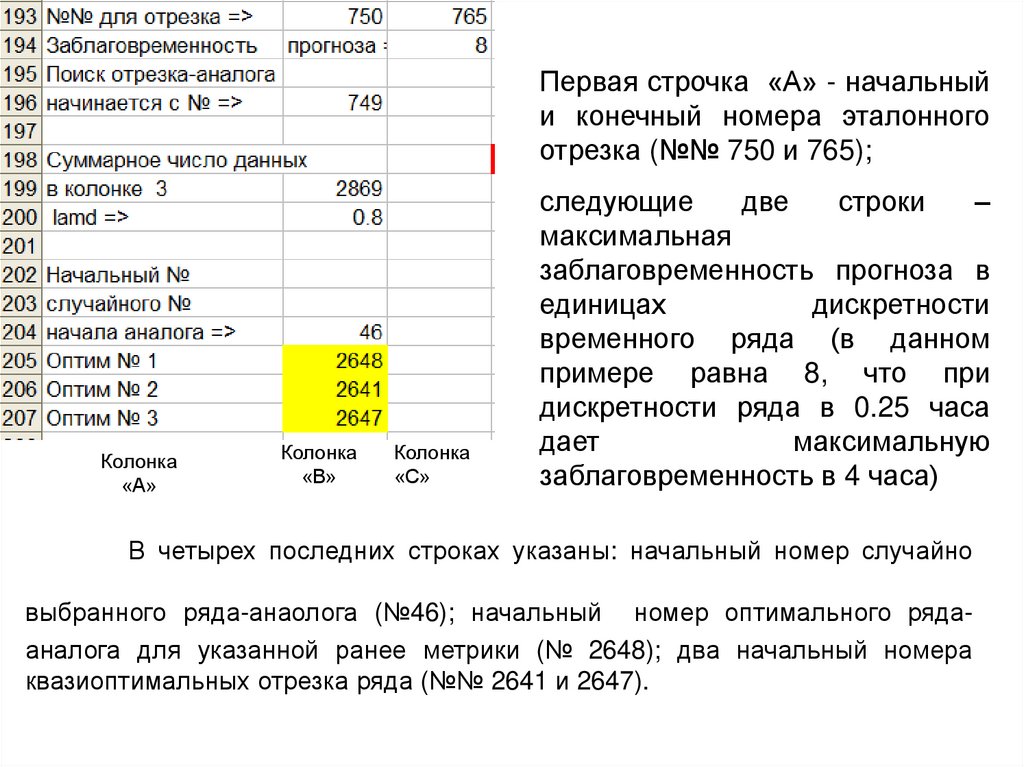
Первая строчка «А» - начальный
и конечный номера эталонного
отрезка (№№ 750 и 765);
Колонка
«А»
Колонка
«В»
Колонка
«С»
следующие
две
строки
–
максимальная
заблаговременность прогноза в
единицах
дискретности
временного ряда (в данном
примере равна 8, что при
дискретности ряда в 0.25 часа
дает
максимальную
заблаговременность в 4 часа)
В четырех последних строках указаны: начальный номер случайно
выбранного ряда-анаолога (№46); начальный номер оптимального рядааналога для указанной ранее метрики (№ 2648); два начальный номера
квазиоптимальных отрезка ряда (№№ 2641 и 2647).

44.

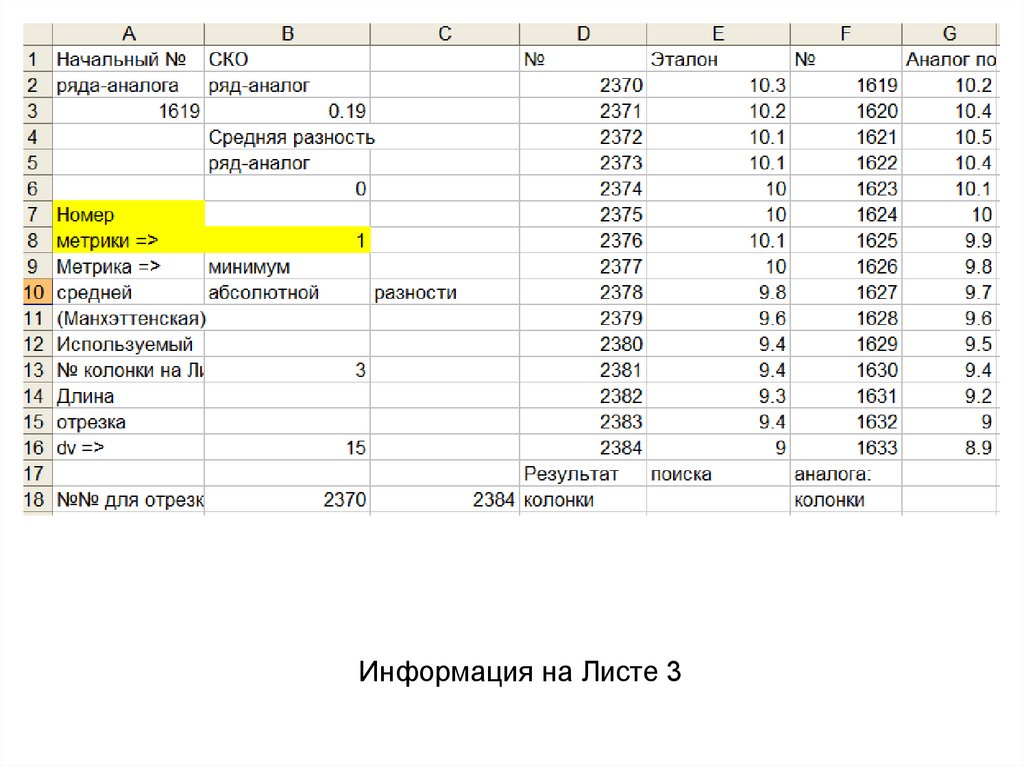
Информация на Листе 3

45.

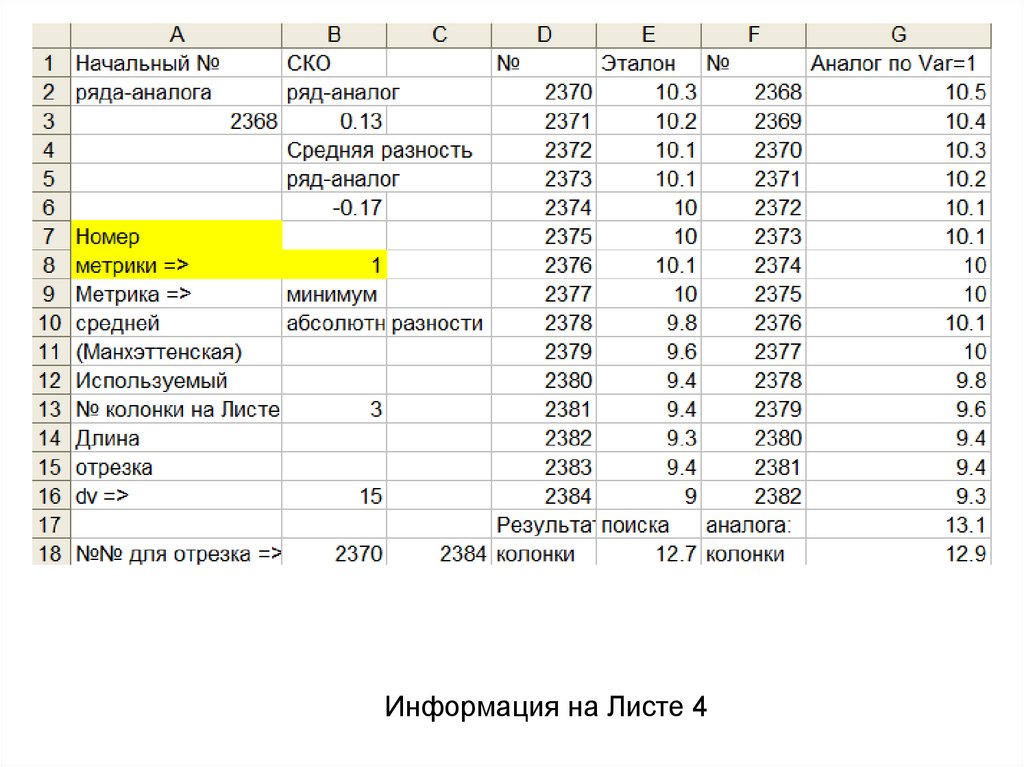
Информация на Листе 4

46.

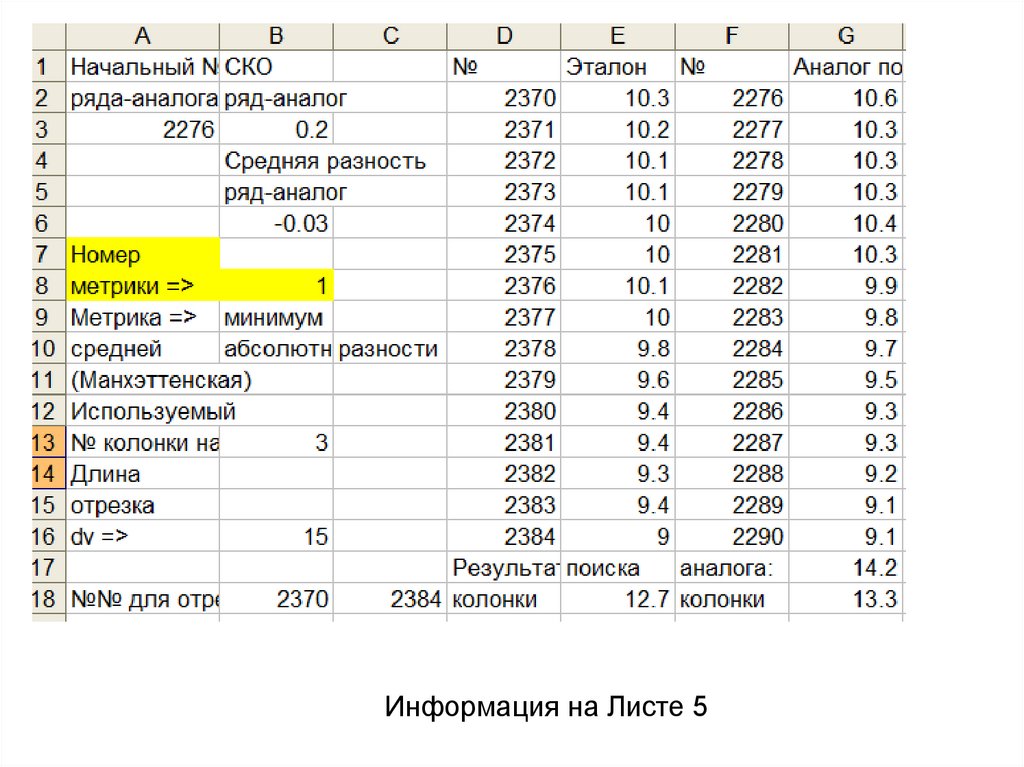
Информация на Листе 5

47.

Проверка работы
различных метрик

48.

Для проверки реализации каждой из 6 используемых метрик
была проведена серия
численный экспериментов. В этих
экспериментах один из фрагментов временного ряда в его начале
заменялся на фрагмент, в точности равным эталону.
После этого проверялось, сможет ли каждый из 6 алгоритмов
его найти.
На следующем слайде показано, как формировался такой
тестовый файл данных.

49.

а)
б)
Фрагмент эталонного (контрольного) участка (№№ с 200 по
220) (а) и его точная копия (№№ с 20 по 40) (б)

50.

а)
б)
в)
Результат определения оптимального отрезка с метриками 1
(а), 2 (б) и 3 (в).

51.

а)
б)
Результат определения оптимального отрезка с
метриками 4 (а) и 5 (в).

52.

Примеры реализации метода
аналогов – среднесуточная
температура СПб

53.

Долее в качестве примера рассмотрены возможности
поиска аналогов во временном ряде среднесуточной
температуры воздуха в СПб.
Использовались данные с 01.02. 1881 по 31.12.1995,
всего 41030 значений.

54.

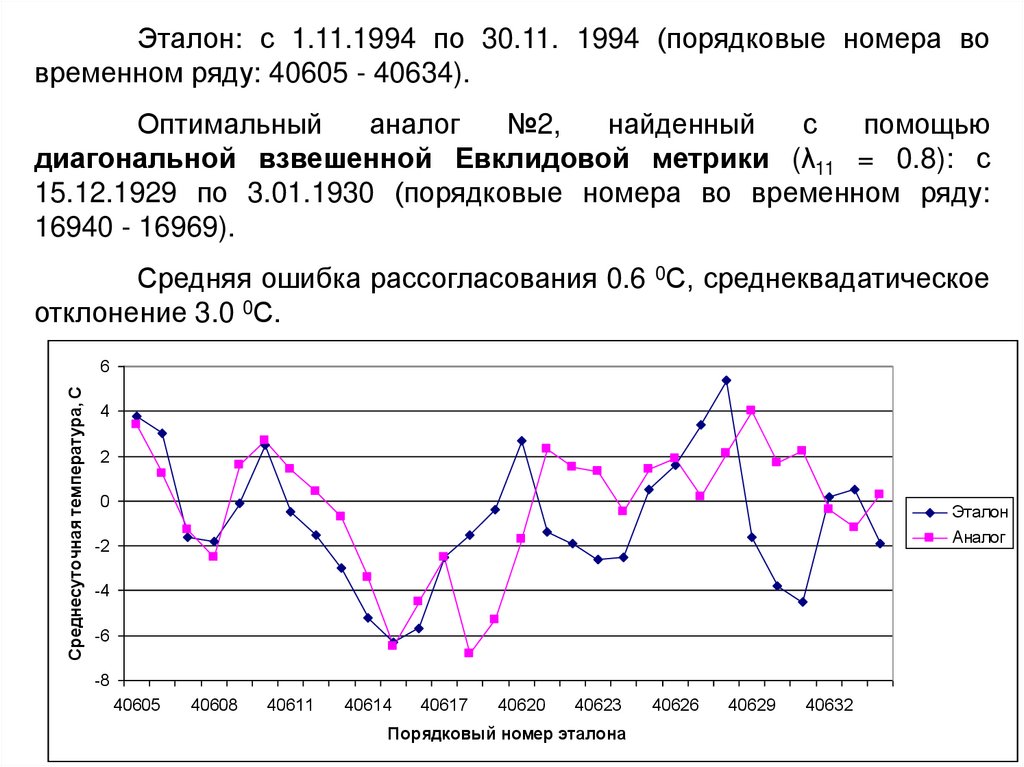
Эталон: с 1.11.1994 по 30.11. 1994 (порядковые номера во
временном ряду: 40605 - 40634).
Оптимальный
аналог
№2,
найденный
с
помощью
диагональной взвешенной Евклидовой метрики (λ11 = 0.8): с
15.12.1929 по 3.01.1930 (порядковые номера во временном ряду:
16940 - 16969).
Средняя ошибка рассогласования 0.6 0С, среднеквадатическое
отклонение 3.0 0С.
Среднесуточная температура, С
6
4
2
0
Эталон
Аналог
-2
-4
-6
-8
40605
40608
40611
40614
40617
40620
40623
Порядковый номер эталона
40626
40629
40632

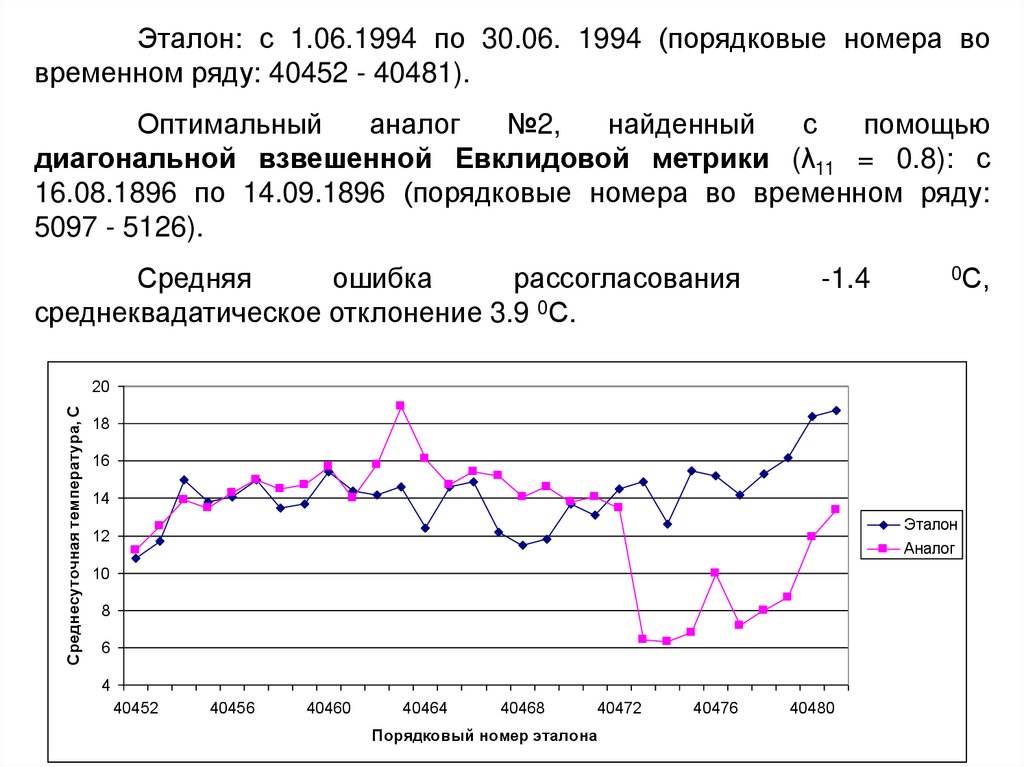
55.

Эталон: с 1.06.1994 по 30.06. 1994 (порядковые номера во
временном ряду: 40452 - 40481).
Оптимальный
аналог
№2,
найденный
с
помощью
диагональной взвешенной Евклидовой метрики (λ11 = 0.8): с
16.08.1896 по 14.09.1896 (порядковые номера во временном ряду:
5097 - 5126).
Средняя
ошибка
рассогласования
среднеквадатическое отклонение 3.9 0С.
-1.4
0С,
Среднесуточная температура, С
20
18
16
14
Эталон
12
Аналог
10
8
6
4
40452
40456
40460
40464
40468
40472
Порядковый номер эталона
40476
40480

56.

Порядок выполнения
лабораторной работы

57.

1. Открыть файл «Аналоги2019.xls», ознакомиться с
формой представления информации на Листах 1-5 и Листе 8.
2. Удалить всю имеющуюся информацию на указанных в
п.1 Листах.
3. Записать на Лист1 выбранный для исследования
временной ряд, запомнить номер колонки с данными и общее
количество членов ряда (параметры nk и nn программы).
4. Запустить выполнение макросов и в диалоговом
режиме
ввести
все
запрашиваемые
параметры
(см.
рекомендации на следующих слайдах).
Расчеты
выполняются
для
трех
вариантов,
последовательно увеличивая длины эталонного отрезка.

58.

Входными параметрами программы «Аналоги2019.xls»
являются:
Номер колонки, в которой на Листе 1 содержится исследуемый
временной ряд: nk.
Общая длина исследуемого временного ряда: nn.
Число искомых аналогов: na (всегда равно 4 и с клавиатуры не
вводится).
Начальный номер отрезка, для которого будет искаться аналог :
n1.
Конечный номер отрезка, для которого будет искаться аналог :
n2.
Начальное значение матрицы в диагонально взвешенной
метрики λ1 : lamd.
Порядок метрики Минковского – параметр p: pmin.

59.

Рекомендации по заданию параметров.
В качестве начального значения матрицы в диагонально
взвешенной метрики λ1 : (параметр lamd) можно ввести
значение 0.8.
Порядок метрики Минковского – параметр p: (параметр
pmin) можно задать равным 1.5.
Число искомых аналогов: (параметр na) всегда равен 4 и не
вводится с клавиатуры.

60.

Поскольку процесс поиска аналогов всегда начинается с
начального номера эталонного отрезка и продолжается до
начала временного ряда (рассматриваются только те значения
временного ряда, которые предшествовали эталону), то номера
n1 и n2 выбираются в конце записанного на Листе ряда.
Например, если общая длина временного ряда равна 2000,
то для варианта №1 можно взять n1= 1900 и n2= 1920, для
варианта №2 можно взять n1= 1880 и n2= 1920, для варианта
№1 можно взять n1= 1850 и n2= 1920.
После выбора значений n1 и n2 для трех вариантов расчета
необходимо
построить
график
используемого
отрезка
временного ряда: для приведенного примера это отрезок 1850 –
1920.

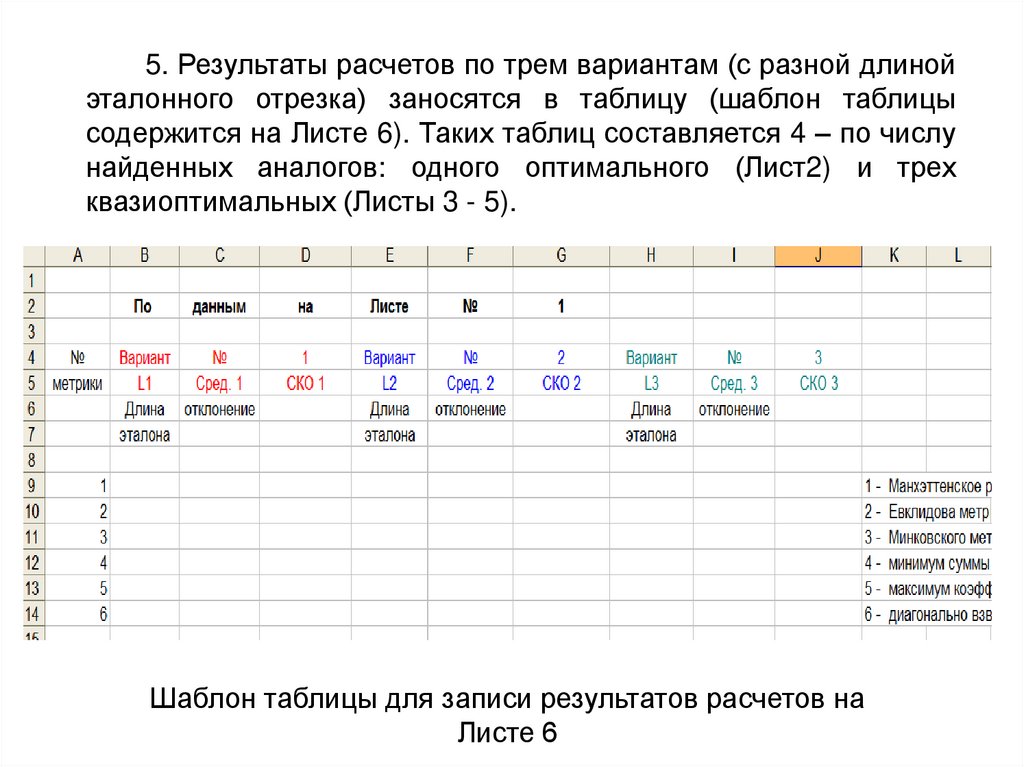
61.

5. Результаты расчетов по трем вариантам (с разной длиной
эталонного отрезка) заносятся в таблицу (шаблон таблицы
содержится на Листе 6). Таких таблиц составляется 4 – по числу
найденных аналогов: одного оптимального (Лист2) и трех
квазиоптимальных (Листы 3 - 5).
Шаблон таблицы для записи результатов расчетов на
Листе 6

62.

6. Проанализировать данные четырех таблиц на предмет
определения:
минимального среднего значения отклонения аналога от
эталона (номер метрики, длина эталона, средняя ошибка);
максимального среднего значения отклонения аналога от
эталона (номер метрики, длина эталона, средняя ошибка);
минимального среднеквадратического отклонения (СКО)
аналога от эталона (номер метрики, длина эталона, СКО);
максимального среднеквадратического отклонения (СКО)
аналога от эталона (номер метрики, длина эталона, СКО);
какая из использованных метрик в среднем для всех
рассмотренных вариантов дает наилучшие и наихудшие
результаты;
какая в среднем зависимость точности совпадения аналога
и эталона от длины эталона.

63.

7. Построить и проанализировать графики:
- по данным на Листе 2 построить график эталона и 6
аналогов (для 6 вариантов метрик) для варианта №1;
- по данным на Листе 2 построить график эталона и 6
аналогов (для 6 вариантов метрик) для варианта №2;
- по данным на Листе 2 построить график эталона и 6
аналогов (для 6 вариантов метрик) для варианта №3;
- по данным на Листе 2 построить график эталона и 6
аналогов (для 6 вариантов метрик) для варианта №1;
- для определенной при выполнении п.6 наилучшей в
среднем метрики (для всех рассмотренных вариантов) по данным
на Листах 2 – 5 построить график эталона и всех найденных
аналогов для варианта №2.

64.

Список цитируемой литературы.
https://cyberleninka.ru/article/n/prognoz-vremennyh-ryadov-sprimeneniem-metoda-analogov
Экспертно-статистическое прогнозирование временных рядов по
методу аналогов, Беляков, Алексей Геннадьевич
Научная библиотека диссертаций и авторефератов disserCat
http://www.dissercat.com/content/ekspertno-statisticheskoeprognozirovanie-vremennykh-ryadov-po-metoduanalogov#ixzz5Opw1qcnS

65.

1. Sankoff D., Kruskal J. Time warps, string edits, and macromolecules: the
theory and practice of sequence comparison. Ontario: Addison Wesley Publ.
Company, 1983. 382 p.
2. Berndt D. J., Clifford J. Using dynamic time warping to find patterns in time
series // KDD workshop on knowledge discovery in databases. 1994. P. 359–
370.
3. Oates T., Firoiu L., Cohen P. R. Clustering time series with hidden Markov
models and dynamic time warping // Proc. of the IJCAI-99 workshop on
neural, symbolic and reinforcement learning methods for sequence learning.
1999. P. 17–21. Вестник СПбГУ. Прикладная математика. Информатика...
2017. Т. 13. Вып. 1 59
4. Maharaj E. A. A significance test for classifying arma models // Journal of
Statistical Computation and Simulation. 1996. Vol. 54, N 4. P. 305–331.
5. Corduas M., Piccolo D. Time series clustering and classification by the
autoregressive metric // Computational Statistics & Data Analysis. 2008. Vol.
52, N 4. P. 1860–1872.

66.

6. Fu T. C. A Review on time series data mining // Engineering Applications of
Artificial Intelligence. 2011. Vol. 24, N 1. P. 164–181.
7. Montero P. M., Vilar J. A. Time series clustering utilities. Feb. 2015. URL: https://
cran.r-project.org/web/packages/TSclust/TSclust.pdf (дата обращения:
01.11.2016).
8. Fan J., Zhang W. Generalised likelihood ratio tests for spectral density //
Biometrika. 2004. Vol. 91, N 1. P. 195–209.
9. Cilibrasi R., Vit`anyi P. M. Clustering by compression // IEEE Transactions on
Information Theory. 2005. Vol. 51, N 4. P. 1523–1545.
10. Alcock R. J., Manolopoulos Y. Time-series similarity queries employing a
feature-based approach // 7th Hellenic Conference on Informatics. 1999. P. 27–29.
11. Сивоголовко Е. В. Методы оценки качества четкой кластеризации //
Компьютерные инструменты в образовании. 2011. №4. С. 14–31.
12. Montero P., Vilar J. TSclust: An R package for time series clustering // Journal
of Statistical Software. 2015. N 62.1. P. 1–43.

67.

Преподаватель дает Вам только «удочку» что, где и когда Вы «поймаете» на нее
будет зависеть только от Вас!

68.

Какие будут вопросы?

69.

Приложение. Модель прогнозирования временных рядов
по выборке максимального подобия
https://habr.com/post/267035/
http://www.mbureau.ru/articles/dissertaciya-model-prognozirovaniyavremennyh-ryadov-glava-2#p_2.2
ИРИНА ЧУЧУЕВА, 13.5.2012
Диссертация «Модель прогнозирования временных рядов по
выборке максимального подобия».

70.

Диссертация «Модель прогнозирования временных рядов по выборке максимального
подобия».
Глава 2. Модели экстраполяции временных рядов по выборке максимального подобия
Глава 1. Постановка задачи и обзор моделей прогнозирования временных рядов
Глава 2. Модели экстраполяции временных рядов по выборке максимального подобия
Глава 3. Метод прогнозирования на модели экстраполяции по выборке максимального
подобия
Глава 4. Программная реализация и оценка эффективности модели экстраполяции по
выборке максимального подобия
Список литературы
Простейший пример реализации в MATLAB рассмотренной ниже модели прогнозирования
временных рядов с подробными комментариями выложен по ссылке Модель
прогнозирования временных рядов по выборке максимального подобия: пояснение и
пример.
Глава 2. Модели экстраполяции временных рядов по выборке максимального подобия
2.1. Модель без учета внешних факторов
2.1.1. Выборки временного ряда
2.1.2. Аппроксимация выборки
2.1.3. Подобие выборок
2.1.4. Описание модели экстраполяции
2.2. Модель с учетом внешних факторов
2.2.1. Выборки временных рядов
2.2.2. Аппроксимация выборки
2.2.3. Подобие выборок
2.2.4. Описание модели
2.3. Варианты моделей по выборке максимального подобия
2.4. Выводы

71.

В модели по выборке максимального подобия предполагается,
что если история повторяется, то для каждой выборки,
предшествующей прогнозу, есть подобная выборка, содержащаяся в
фактических значениях этого же временного ряда. Формально это
называется гипотеза подобия

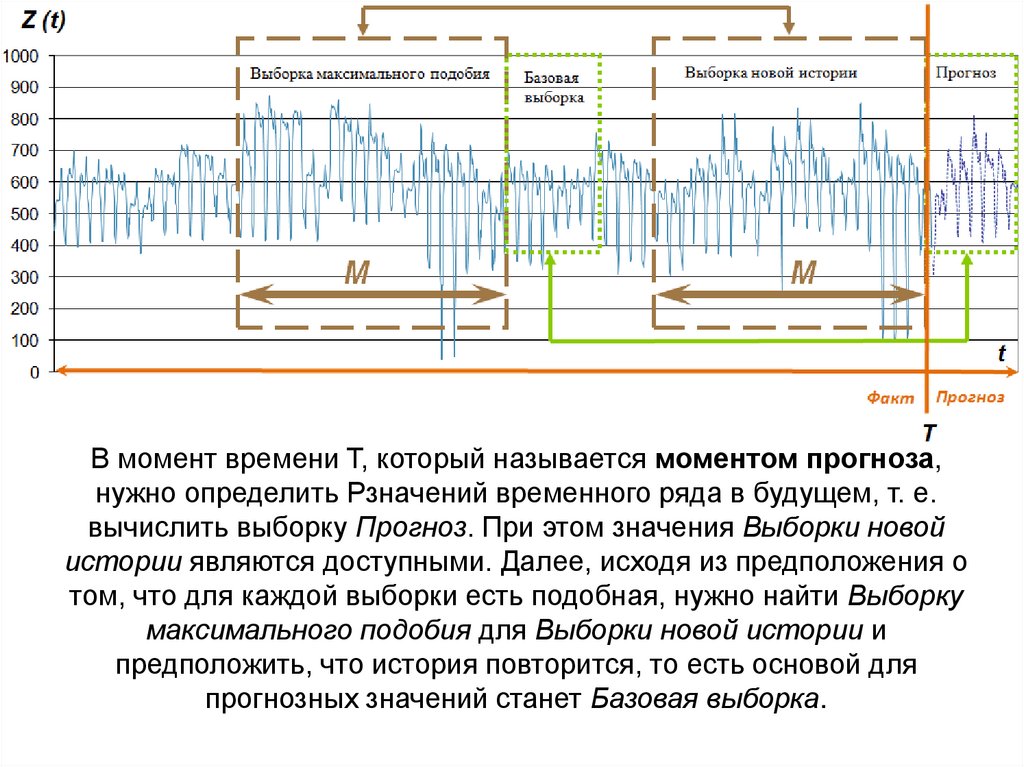
72.

73.

Метод максимума коэффициента корреляции
В своей диссертации я предлагаю самый простой вариант
определения подобия — вычисление значения линейной
корреляции. Берем одну выборку длины M, берем другую выборку
длины M, считаем значение корреляции, которое и будет отражать
подобие двух выборок.
Искать Выборку максимального подобия проще всего методом
перебора среди всех возможных выборок. Для временных рядов
до 100 000 значений такого сорта перебор занимает несколько
секунд при реализации на персональном компьютере средней
мощности.

74.

Корректировка связи элементов эталонной и оптимальной
выборок
Самым простым вариантом корректировки связи элементов
эталонной (вектор y) и оптимальной (вектор x) выборок
является предположением о наличии линейной их связи:
y i a1 xi a0 i
i = 1, 2, … , k;
где k - количество элементов временного ряда, содержащихся в
эталонном или оптимальном его отрезках.
Численные значения коэффициентов a1 и a0 после
определения оптимального отрезка можно вычислить, например, с
использованием метода наименьших квадратов, минимизирую
значение функции двух переменных S(a1, a0):
k
k
S ( a1 , a0 ) ( y j y j ) ( a1 xi a0 y j ) 2
j 1
2
j 1

75.

Если уравнение (1) отражает зависимость элементов двух
выборок x и y при помощи коэффициентов a1 и a0, то на основании
предположения о подобии и прогностическая выборка (значения
временного ряда, стоящие по времени после последнего значения
этой выборки) так же может быть скорректирована аналогичным
образом с использованием уже найденных коэффициентов:
(3)
y l k a1 xl k a0
где k - количество элементов временного ряда, содержащихся в
эталонном или оптимальном его отрезках; i = 1, 2, … , p; максимальная
p – заблаговременность прогноза в единицах дискрентности
временного ряда.

76.

Название модели на английском звучит как extrapolation (или
forecast) model on the most similar pattern, сокращенно EMMSP.
Самое важное свойство предложенной модели — ее простота
и наглядность.

77.

Приложение. Распознавание образов.

78.

В целом, можно выделить три метода распознавания
образов.
Метод перебора. В этом случае производится сравнение
с базой данных, где для каждого вида объектов представлены
всевозможные его модификации.
Второй подход - производится более глубокий анализ
характеристик образа.
Третий
метод
использование
искусственных
нейронных сетей (ИНС). Этот метод требует либо большого
количества примеров задачи распознавания при обучении, либо
специальной структуры нейронной сети, учитывающей
специфику данной задачи. Тем не менее, его отличает более
высокая эффективность и производительность.

79.

Измерения, используемые для классификации образов,
называются признаками.
Признак – это некоторое количественное измерение
объекта произвольной природы.
Совокупность признаков, относящихся к одному образу,
называется вектором признаков.
Вектора признаков принимают значения в пространстве
признаков.
В рамках задачи распознавания считается, что каждому
образу ставится в соответствие единственное значение вектора
признаков и наоборот: каждому значению вектора признаков
соответствует единственный образ.

80.

Классификатором или решающим правилом называется
правило отнесения образа к одному из классов на основании его
вектора признаков.
Задача генерации признаков – это выбор тех признаков,
которые с достаточной полнотой (в разумных пределах) описывают
образ.
Задача селекции признаков – отбор наиболее информативных
признаков для классификации.
Задача построения классификатора – выбор решающего
правила, по которому на основании вектора признаков
осуществляется отнесение объекта к тому или иному классу.
Задача количественной оценки системы (выбранные
признаки + классификатор) с точки зрения правильности или
ошибочности классификации.

81.

Принцип сравнения с эталоном - один из первых
подходов, возникших при построении технических систем
распознавания.
По физической природе характеристик-признаков образов
системы
распознавания подразделяются на простые и сложные.
Сложные
системы
распознавания
одноуровневыми и многоуровневыми.
могут
быть
В одноуровневых системах распознавание осуществляется
на основе одного словаря признаков одним алгоритмом
распознавания.
В многоуровневых системах результаты распознавания,
полученные на одном этапе, используются в качестве исходных
данных на следующем.

82.

Другой вариант задания весов - вычисление веса Wi, с
которыми каждый из векторов ki учитывается при построении
прогноза: они зависят от расстояния до предыстории y по формуле:
(k , y ) 2
i
Wi 1
( k k 1 , y )
2
где ρ(ki, y) — расстояние до i-го ближайшего соседа. Для нормировки
весов Wi, вычислим их общую сумму и поделим каждый из весов на
нее:
Wi
wi t
W j
j 1
Прогноз:
.
t
x n 1 wi k i
i 1

83.

В АКМ используется следующий вид прогноза:
где
Веса предлагается брать адаптированными:

84.

Реализовано два варианта использованием трех
прогностических отрезков для каждого из 6 критериев.
Каждый прогностический отрезок строился для
каждого критерия как суперпозиция (осреднение) трех
последовательно найденных оптимальных аналогов.
- как простое среднее трех последовательно
найденных прогностических отрезков: оптимального и
двух квазиоптимальных;
- как среднее взвешенное трех последовательно
найденных прогностических отрезков: оптимального и
двух квазиоптимальных с убывающими весами:
w1 = 0.5 (для оптимального);
w2 = 0.3 (для первого квазиоптимального);
w3 = 0.2 (для второго квазиоптимального).

85.

Таким образом в программе «Поиск всех
аналогов.xls» адаптивной композиции моделей
прогноз реализуется по двум следующим алгоритмам:
1. Прогностический отрезок – простое среднее трех
последовательно найденных прогностических отрезков:
оптимального и двух квазиоптимальных.
2. Прогностический отрезок – среднее взвешенное двух
последовательно найденных прогностических отрезков:
оптимального и двух квазиоптимальных с убывающими
весами:
w1 = 0.5; w2 = 0.3; w3 = 0.2.
.

English Русский Rules