Презентация по математике _Комбинаторные задачи_

1. Комбинаторные задачи

2. Комбинаторные задачи

Цель работы: изучить основные понятия комбинаторики и
способы решения некоторых комбинаторных задач
План работы:
Что такое комбинаторика
Примеры комбинаторных задач

3. Что такое комбинаторика

Комбинаторика - ветвь математики, изучающая комбинации и
перестановки предметов, возникла в 17 веке. Комбинаторику как
самостоятельный раздел математики первым стал рассматривать немецкий
философ и математик Г.Лейбниц в своей работе «Об искусстве
комбинаторики», опубликованной в 1666 году. Он же впервые ввел термин
«комбинаторика».
Сейчас комбинаторика находит применение во многих областях науки
и жизни людей. Занимается выбором объектов и расположением их в том
или ином порядке. Комбинаторные методы используются для решения
задач по составлению транспортных расписаний.

4. Методы решения комбинаторных задач

- решение методом перебора;
- решение с помощью дерева возможных вариантов;
- решение с помощью комбинаторного правила умножения;
- решение с помощью таблиц.

5. Перебор возможных вариантов

1. Какие двухзначные числа можно составить из цифр: 2, 5, 7?
Ответ: 22, 25, 27, 52, 55, 57, 72, 75, 77.
2. В финальном забеге на 100 метров участвуют Иванов, Громов и Орлов. Назовите
все возможные варианты распределения призовых мест.
В. 1: 1) Иванов 2) Громов 3) Орлов;
В. 2: 1) Иванов 2) Орлов 3) Громов;
В. 3: 1) Громов 2) Иванов 3) Орлов;
В. 4: 1) Громов 2) Орлов 3) Иванов;
В. 5: 1) Орлов 2) Громов 3) Иванов;
В. 6: 1) Орлов 2) Иванов 3) Громов.
Ответ: 6 вариантов распределения.

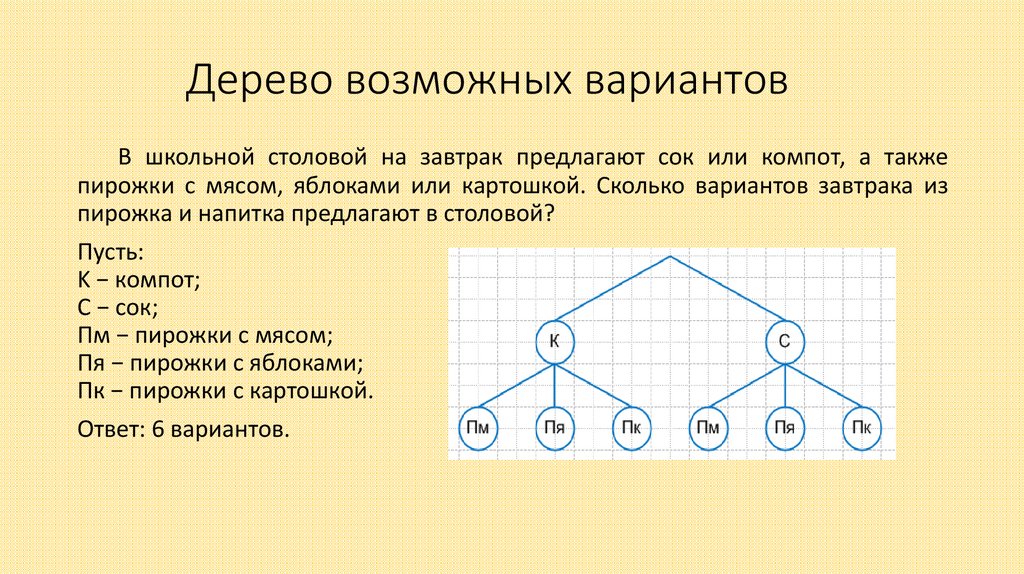
6. Дерево возможных вариантов

В школьной столовой на завтрак предлагают сок или компот, а также
пирожки с мясом, яблоками или картошкой. Сколько вариантов завтрака из
пирожка и напитка предлагают в столовой?
Пусть:
K − компот;
С − сок;
Пм − пирожки с мясом;
Пя − пирожки с яблоками;
Пк − пирожки с картошкой.
Ответ: 6 вариантов.

7. Решение с помощью комбинаторного правила умножения

Шесть учеников сдают зачет по математике. Сколькими способами их
можно расположить в списке?
Первым в списке может оказаться любой из 6 учеников, вторым в списке
может быть любой из оставшихся 5 учеников, третьим - любой из оставшихся 4
учеников, четвертым - любой из оставшихся 3 учеников, пятым - любой из
оставшихся 2 учеников, шестым - последний 1 ученик.
Решение: : 6 х 5 х 4 х 3 х 2 х 1 = 720.
Ответ: 720 способами.

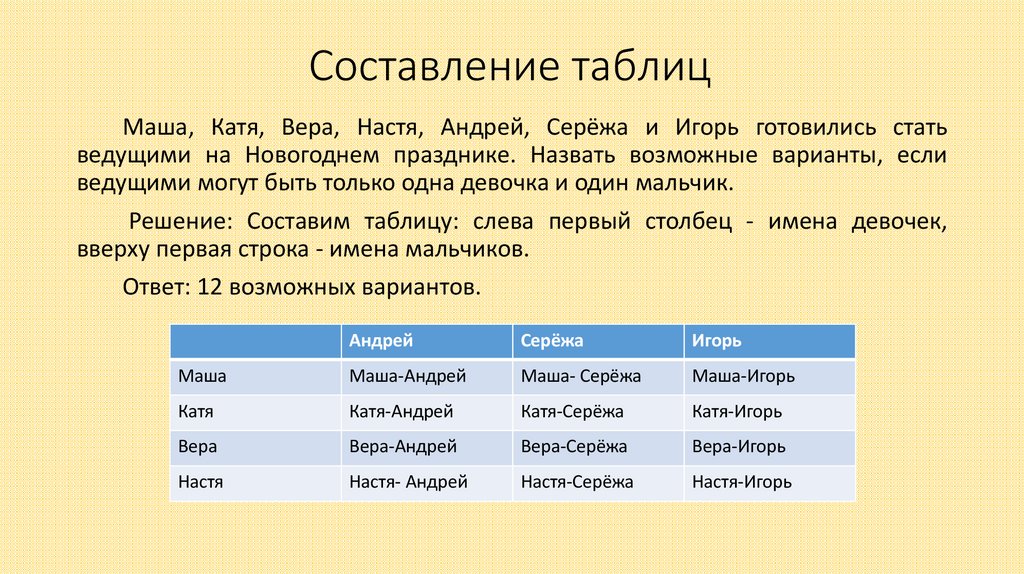
8. Составление таблиц

Маша, Катя, Вера, Настя, Андрей, Серёжа и Игорь готовились стать
ведущими на Новогоднем празднике. Назвать возможные варианты, если
ведущими могут быть только одна девочка и один мальчик.
Решение: Составим таблицу: слева первый столбец - имена девочек,
вверху первая строка - имена мальчиков.
Ответ: 12 возможных вариантов.
Андрей
Серёжа
Игорь
Маша
Маша-Андрей
Маша- Серёжа
Маша-Игорь
Катя
Катя-Андрей
Катя-Серёжа
Катя-Игорь
Вера
Вера-Андрей
Вера-Серёжа
Вера-Игорь
Настя
Настя- Андрей
Настя-Серёжа
Настя-Игорь

9. Спасибо за внимание!