Similar presentations:
История комбинаторики. Способы решения комбинаторных задач
1.
Каждыйучастник берет фишки:
Точилка - столько, сколько взяли
Игрушка – в два раза больше
Ручка – в 4 раза больше
2.
3.
4. История комбинаторики. Способы решения комбинаторных задач.
5. Цель работы
Изучение методов комбинаторики и ихприменение при решении занимательных
задач, головоломок и математических
фокусов.
6. Задачи
Ознакомиться с теоретическим материаломпо данной проблеме.
Отработать полученные теоретические
знания при решении задач.
Изучить наиболее интересные и
увлекательные фокусы и занимательные
задачи, основанные на методах
комбинаторики
7.
История комбинаторики освещаетразвитие комбинаторики. Начав с
анализа головоломок и азартных игр,
комбинаторика оказалась
исключительно полезной для решения
практических задач почти во всех
разделах математики. Кроме того
комбинаторные методы оказались
полезными в статистике, генетике,
лингвистике и многих других науках.
8.
Комбинаторные задачивозникали и в связи с
такими играми, как шашки,
шахматы, домино, карты,
кости и т.д. (Например,
задача о расстановке
восьми ферзей на
шахматной доске так, чтобы
ни один из них не оказался
под боем, об обходе всех
полей доски шахматным
конем и т.д.
9. Комбинаторные мотивы можно заметить в символике китайской «Книге Перемен» (V век до н.э.) Историки отмечают также комбинаторные
проблемы в руководствах по игре в Го идругих играх.
Большой интерес математиков многих стран с древних времен неизменно вызывали
магические квадраты- это квадратные таблицы из целых чисел, в которых сумма во
всех столбцах, строках и двух главных диагоналях равна одному и тому же числу.
10.
Термин "комбинаторика" былвведён в математический обиход
знаменитым Лейбницем.
Готфрид Вильгельм Лейбниц
(1.07.1646 - 14.11.1716) - всемирно
известный немецкий учёный,
занимался философией,
математикой, физикой,
организовал Берлинскую
академию наук и стал её первым
президентом.
11.
В XVIII веке к решениюкомбинаторных задач
обращались выдающиеся
математики. Так, Леонард
Эйлер рассматривал
задачи о разбиении чисел,
о паросочетаниях, о
циклических расстановках,
о построении магических и
латинских квадратов.
12. «ОСОБАЯ ПРИМЕТА» КОМБИНАТОРНЫХ ЗАДАЧ
«Особая примета» комбинаторных задач— вопрос, который всегда можно
сформулировать так, чтобы он
начинался словами: «Сколькими
способами...».
13.
Способырешения комбинаторных
задач:
Перебор возможных вариантов
Дерево возможных вариантов
Составление таблиц
Правило умножения
В пятом классе для решения
комбинаторных задач мы
используем метод перебора
14. Перебор возможных вариантов
Задача .В финальном забеге на 100 м участвуют Иванов, Громов и Орлов.
Назовите возможные варианты распределения призовых мест.
Ответ:
Вариант1: 1) Иванов, 2) Громов, 3) Орлов.
Вариант2: 1) Иванов, 2) Орлов, 3) Громов.
Вариант3: 1) Орлов, 2) Иванов, 3) Громов.
Вариант4: 1) Орлов, 2) Громов, 3) Иванов.
Вариант5: 1) Громов, 2) Орлов, 3) Иванов.
Вариант6: 1) Громов, 2) Иванов, 3) Орлов.
Задача 3.
В кружок бального танца записались Петя, Коля, Витя, Олег, Таня, Оля,
Наташа, Света. Какие танцевальные пары девочки и мальчика могут
образоваться?
Ответ:
1) Таня - Петя, 2) Таня - Коля, 3) Таня - Витя, 4) Таня - Олег, 5) Оля - Петя,
6) Оля - Коля, 7) Оля - Витя, 8) Оля - Олег, 9) Наташа - Петя, 10) Наташа Коля, 11) Наташа - Витя, 12) Наташа - Олег, 13) Света - Петя, 14) Света Коля, 15) Света - Витя, 16) Света - Олег.
15.
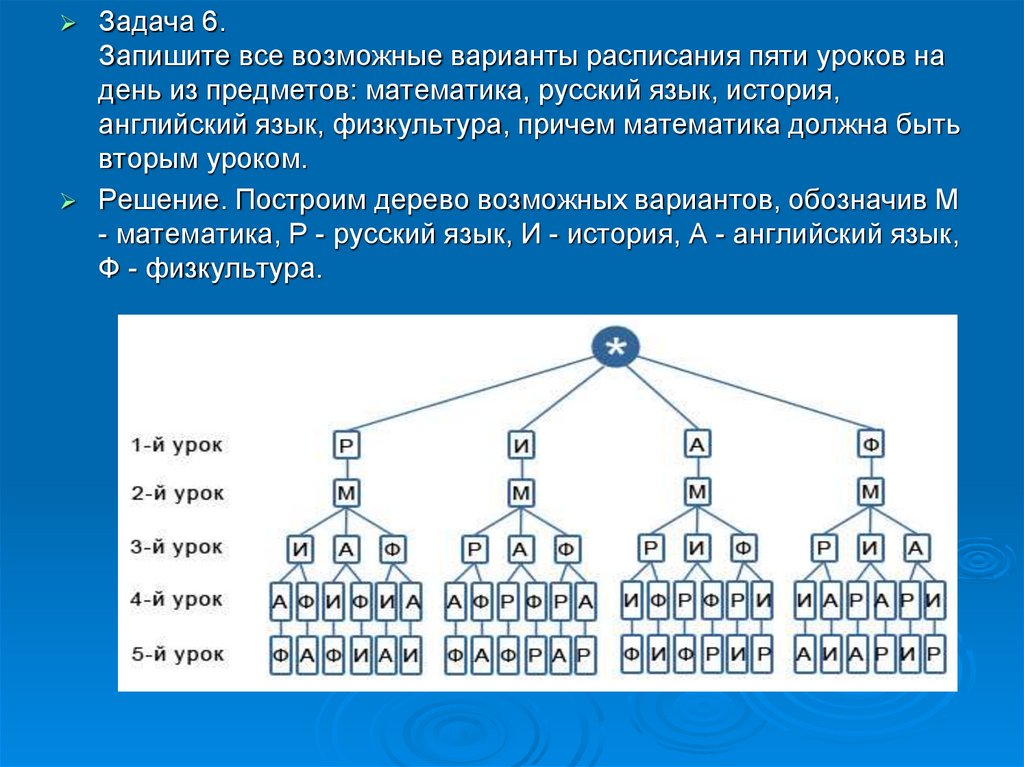
Задача 6.Запишите все возможные варианты расписания пяти уроков на
день из предметов: математика, русский язык, история,
английский язык, физкультура, причем математика должна быть
вторым уроком.
Решение. Построим дерево возможных вариантов, обозначив М
- математика, Р - русский язык, И - история, А - английский язык,
Ф - физкультура.
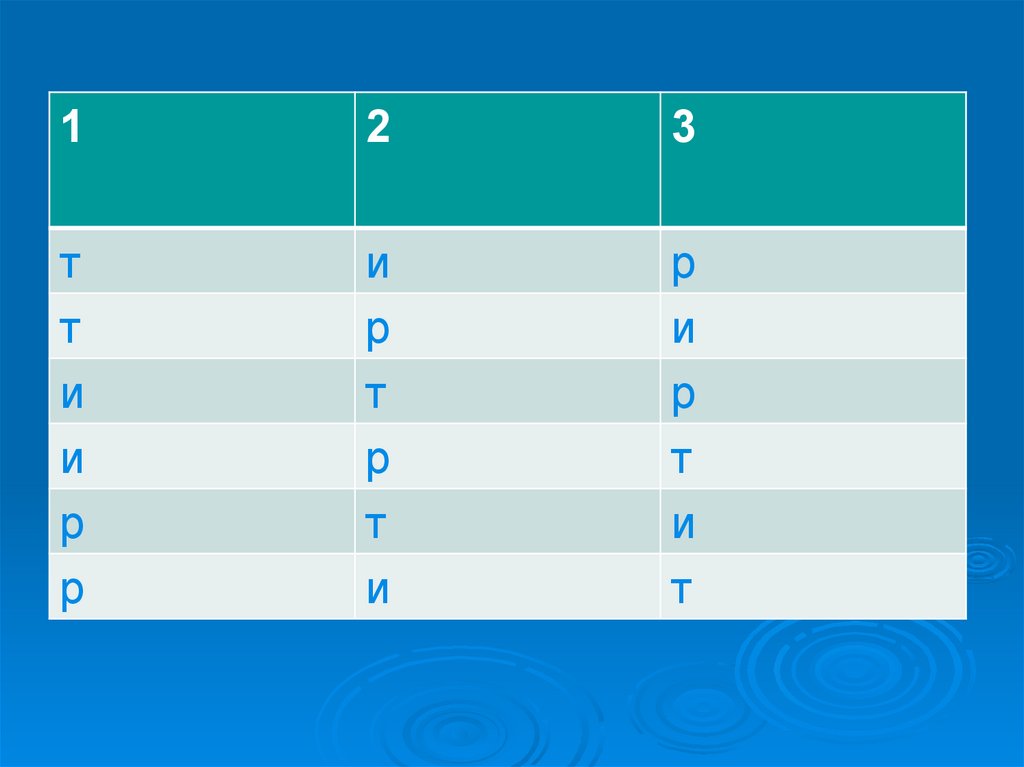
16.
12
3
т
т
и
и
р
р
и
р
т
р
т
и
р
и
р
т
и
т
17.
Комбин.Число взятых орехов
Итого Остаток
тир
1+1=2
2+4=6
3+12=15
23
1
три
1+1=2
2+8=10
3+6=9
21
3
итр
1+2=3
2+2=4
3+12=15
22
2
ирт
1+2=3
2+8=10
3+3=6
19
5
рти
1+4=5
2+2=4
3+6=9
18
6
рит
1+4=5
2+4=6
3+3=6
17
7
18.
Номер парыРасположение
1
Обе карты в 1 ряду
2
Обе карты во 2 ряду
3
Обе карты в 3 ряду
4
Обе карты в 4 ряду
5
Одна в 1 ряду и одна во 2 ряду
6
Одна в 1 ряду и одна в 3 ряду
7
Одна в 1 ряду и одна в 4 ряду
8
Одна во 2 ряду и одна во 3 ряду
9
Одна во 2 ряду и одна в 3 ряду
10
Одна в 3 ряду и одна в 4 ряду
19.
НАУКАУМЕЕТ
МНОГО
ГИТИК
20.
Учебныезаведения – составление
расписаний
Азартные игры – подсчет частоты
выигрышей
Экономика – анализ вариантов куплипродажи акций
Сфера питания- составление меню
Биология – расшировка кода ДНК
Военное дело – расположение
подразделений и т.д.
21. Выводы:
. Изучение комбинаторики представляет огромныйинтерес для учащихся всех возрастов.
2. Существует множество способов решения
комбинаторных задач, каждый из которых
применяется для решения определенного типа
задач.
3. С помощью методов комбинаторики можно решать
и создавать новые занимательные математические
задачи и фокусы.
3. Комбинаторика - один из разделов математики,
который имеет самое широкое практическое
применение во всех отраслях производства и жизни
человека.



















 informatics
informatics