Комбинаторные алгоритмы перестановки повторениями

1.

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
ИНСТИТУТ МАТЕМАТИКИ И ИНФОРМАЦИОННЫХ СИСТЕМ
КУРСОВАЯ
РАБОТА
К О М Б И Н А Т О Р Н Ы Е
А Л Г О Р И Т М Ы
П Е Р Е С Т А Н О В К И
П О В Т О Р Е Н И Я М И
В Ы П О Л Н И Л
С Т У Д Е Н Т
Р У К О В О Д И Т Е Л Ь
Г Р У П П Ы
К . Т. Н . ,
С
П М И Б - 2 3
Д О Ц Е Н Т
К А Ф Е Д Р Ы
П М И
К .
А .
П О П О В А
И .
А .
П У Ш К А Р Е В

2.

ВВЕДЕНИЕ
Ц Е Л И И З А Д АЧ И
Комбинаторика влияет на множество областей, включая информатику и теорию
алгоритмов.
Основное направление работы — генерация перестановок с повторениями,
полезное для задач размещения однотипных элементов.
Мы рассмотрим основы комбинаторики и перестановок, теоретические аспекты
комбинаторных алгоритмов генерации перестановок с повторениями.
Также мы разработаем алгоритм генерации перестановок с повторениями на языке
программирования С++.

3.

О С Н О В Ы К О М Б И Н АТО Р И К И
Комбинаторика — раздел математики, изучающий комбинаторные
структуры и методы для работы с ними.
Важными элементами комбинаторики являются перестановки, сочетания,
размещения.
Комбинаторика применяется в различных областях, включая теорию
алгоритмов.

4.

П Е Р Е С Т А Н О В К И И И Х З Н АЧ Е Н И Е
Перестановка — упорядоченное множество элементов.
Для множества {1, 2, 3} существует 3! = 6 различных перестановок:
{1, 2, 3}, {1, 3, 2}, {2, 1, 3}, {2, 3, 1}, {3, 1, 2}, {3, 2, 1}
Перестановки играют важную роль в задачах, таких как распределение объектов.
Существуют также перестановки с повторениями, которые моделируют ситуации с
однотипными объектами.
В слове "МАМА" 6 перестановок с повторениями: "МАМА", "АММА", "АМАМ" и др.

5.

К О М Б И Н АТО Р Н Ы Е А Л ГО Р И Т М Ы
Комбинаторные алгоритмы используются для решения задач, связанных с
распределением элементов в различных порядках.
В комбинаторике широко используются и являются ключевыми понятиями
при вычислении числа перестановок факториал
n! = n * (n-1) * (n-2) * … * 2 * 1
и биномиальный коэффициент

6.

Р Е К У Р С И В Н Ы Й М Е ТО Д Г Е Н Е РА Ц И И
П Е Р Е СТА Н О ВО К С П О ВТО Р Е Н И Я М И
Входные данные:
n – количество элементов
k – длина перестановок с повторениями
Результат:
все k-последовательности множеств {1, 2, …, n}

7.

Пусть n = 5, найти 3-перестановки
FIND(n, 2) вернет 2-перестановки:
3-перестановки:
11 12 13 14 15
111 112 113 114 115
211 212 213 214 215
21 22 23 24 25
121 122 123 124 125
221 222 223 224 225
31 32 33 34 35
131 132 133 134 135
231 232 233 234 235
41 42 43 44 45
141 142 143 144 145
241 242 243 244 245
51 52 53 54 55
151 152 153 154 155
251 252 253 254 255
проделав то же самое с 3, 4, 5 получим все 3-перестановки

8.

Р Е А Л И З А Ц И Я Р Е К У РС И В Н О ГО
А Л ГО Р И Т М А П Е Р Е СТА Н О ВО К С
П О ВТО Р Е Н И Я М И
Ввод множества элементов и длину перестановок в теле программы.
Множество {1, 2, 3} и 3 перестановки:

9.

П Р И М Е Р Ы З А Д АЧ
Найти все возможные комбинации из 2-х шахматных фигур (ладья, слон, ферзь),
учитывая, что одна и та же фигура может быть выбрана несколько раз.

10.

Найти все возможные комбинации из трех букв слова "ABCD", учитывая,
что буквы могут повторяться.

11.

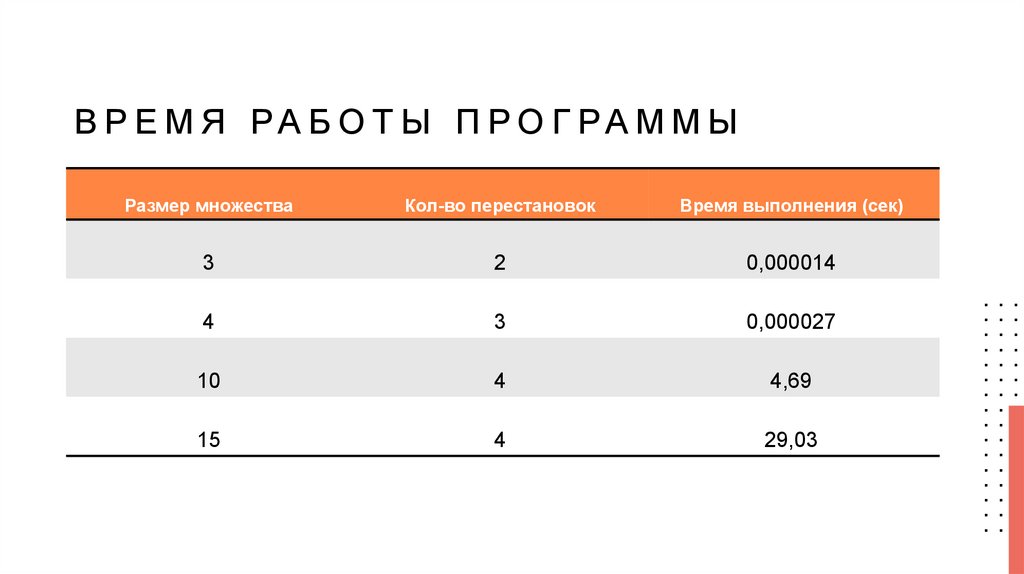
В Р Е М Я РА Б О Т Ы П Р О Г РА М М Ы
Размер множества
Кол-во перестановок
Время выполнения (сек)
3
2
0,000014
4
3
0,000027
10
4
4,69
15
4
29,03

12.

ЗАКЛЮЧЕНИЕ
Изучены основы комбинаторики и перестановок с повторениями.
Разработана программа на C++, генерирующая перестановки с
повторениями.
Эксперименты подтвердили корректную и эффективную работу
программы.
Результаты работы имеют важное значение для различных областей и
решения задач с перестановками с повторениями.

13.

С П И С О К Л И Т Е РАТ У Р Ы
Knuth, Donald E. "The "The Art of Computer Programming, Volume 4, Fascicle 2:
Generating All Tuples and Permutations." Addison-Wesley Professional, 2005.
Grimaldi, Ralph P. "Discrete and Combinatorial Mathematics: An Applied Introduction."
Addison-Wesley, 2017.