Тема 2.1 Шифрование методами перестановки

1. Симметричные криптосистемы

1
Тема 2
Симметричные
криптосистемы
Часть 1
Шифрование методами
перестановки

2.

Содержание
1. Простая перестановка
2. Одиночная перестановка по ключу
3. Двойная перестановка
4. Магический квадрат
5. Шифр Кардано
6. Шифр Ришелье
2

3.

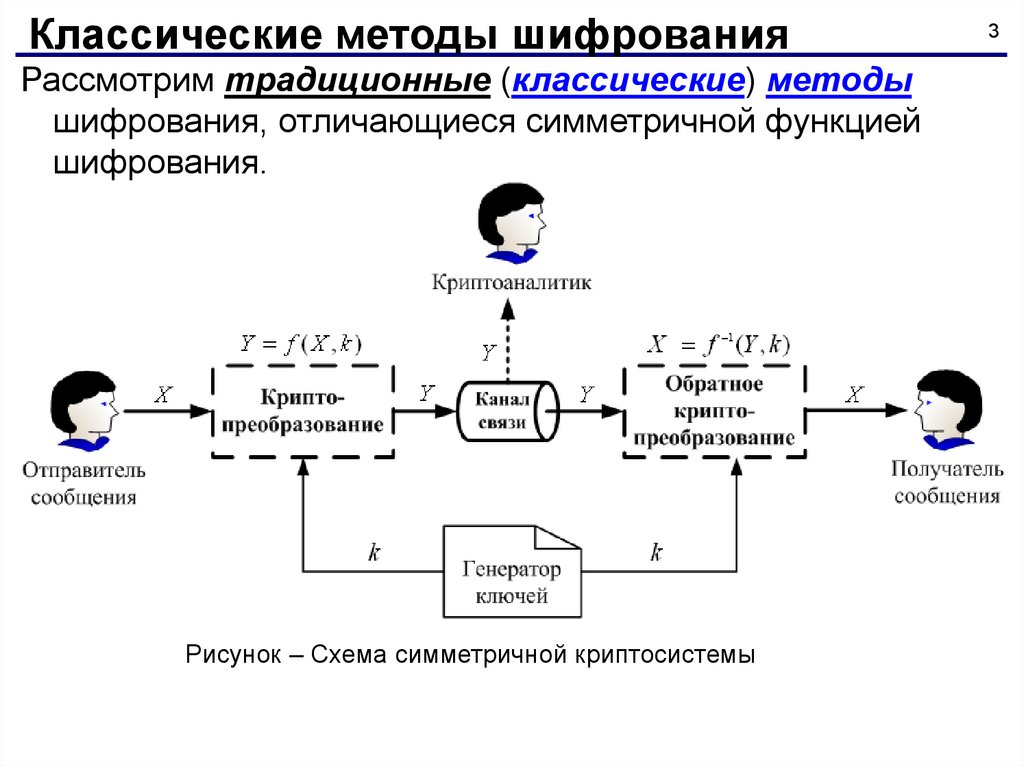
Классические методы шифрования
Рассмотрим традиционные (классические) методы
шифрования, отличающиеся симметричной функцией
шифрования.
Рисунок – Схема симметричной криптосистемы
3

4.

Классические методы шифрования
Все традиционные криптографические системы можно
подразделить на:
1. Шифры перестановки:
1.1. Шифр перестановки “скитала” (цилиндр + намотанная кожа).
1.2. Шифрующие таблицы (запись символов алфавита в матрицу).
1.3. Применение магических квадратов.
2. Шифры простой замены:
2.1. Полибианский квадрат.
2.2. Система шифрования Цезаря.
2.3. Аффинная система подстановок Цезаря.
2.4. Система Цезаря с ключевым словом.
2.5. Шифрующие таблицы Трисемуса.
2.6. Биграммный шифр Плейфера.
2.7. Криптосистема Хилла.
2.8. Система омофонов.
4

5.

Классические методы шифрования
3. Шифры сложной замены:
3.1. Шифр Гронсфельда.
3.2. Система шифрования Вижинера.
3.3. Шифр “двойной квадрат” Уитстона.
3.4. Одноразовая система шифрования.
3.5. Шифрование методом Вернама.
3.6. Роторные машины.
4. Шифрование методом гаммирования.
5. Шифрование, основанное на аналитических преобразованиях
шифруемых данных.
5

6.

Классические методы шифрования
6
Современные симметричные одноключевые
криптоалгоритмы базируются на принципах, изложенных в
работе К.Шеннона «Теория связи в секретных системах»
(1949), где он обобщил накопленный до него опыт
разработки шифров.
Оказалось, что даже в сложных шифрах в качестве
составных компонентов можно выделить
шифры простой и сложной замены,
шифры перестановки,
а также некоторые их модификации и комбинации.
Следует отметить, что комбинации шифров
перестановок и шифров замены образуют все
многообразие применяемых на практике симметричных
шифров.

7.

Классические методы шифрования
Рассмотрим примеры шифров каждой группы в
хронологическом порядке, что позволит понять суть этих
методов на простых и наглядных примерах из истории
развития криптографии.
7

8.

8
1. Шифрующие таблицы

9.

Идея шифров перестановки
Шифры типа перестановки применялись еще с античных
времен, и особенно активно в эпоху Возрождения (конец
XIV столетия) .
Идея шифра перестановки состоит в том, что
при зашифровании буква ai открытого текста
переходит не в фиксированный знак алфавита,
а в другую букву того же открытого текста, скажем aj ,
в результате чего буквы располагаются на новых
местах, т.е. переставляются.
В разработанных шифрах перестановки эпохи Возрождения
применяются шифрующие таблицы, которые, в сущности,
также задают правила перестановки букв в исходном
сообщении.
9

10.

Ключ
10
В качестве ключа в шифрующих таблицах используются:
размер таблицы,
слово или фраза,
задающие
перестановку,
особенности структуры таблицы.

11.

Простая перестановка
11
Одним из самых примитивных табличных шифров
перестановки является простая перестановка.
Для нее ключом служит размер таблицы.
Открытое сообщение записывается в таблицу
посимвольно в ячейки таблицы по столбцам.
После заполнения таблицы текстом сообщения по
столбцам для формирования шифротекста считывают
содержимое таблицы по строкам.
Естественно, отправитель и получатель сообщения
должны заранее условиться об общем ключе в виде
размера таблицы.
При расшифровывании действия выполняют в
обратном порядке.

12.

Простая перестановка
12
Для заполнения пустых клеток (если объём текста
меньше ёмкости таблицы) можно использовать любые
символы.
Если текст не помещается в таблицу целиком, его
разбивают на блоки длиной, равной количеству ячеек
таблицы, добавляя при необходимости нужное
количество символов.
Поскольку количество вариантов различных ключей
относительно невелико, стойкость такого алгоритма
шифрования невысока.

13.

Простая перестановка
13
Пример.
Сообщение
ПОЛОЦКИЙ ГОСУДАРСТВЕННЫЙ
АГРАРНО-ЭКОНОМИЧЕСКИЙ КОЛЛЕДЖ
записывается в таблицу посимвольно в ячейки таблицы по
столбцам.
Результат заполнения таблицы из 5 строк и 10 столбцов показан
ниже.
П
О
Л
О
Ц
К
И
Й
Г
О
У
Д
А
Р
С
Т
В
Е
Н
Н
Ы
Й
А
Г
Р
А К И
Р О Ч
Н Н Е
О О С
Э М К
И Л
Й Е
К Д
О Ж
Л

14.

Простая перестановка
П
О
Л
О
Ц
К
И
Й
Г
О
У
Д
А
Р
С
Т
В
Е
Н
Н
Ы
Й
А
Г
Р
14
А К И
Р О Ч
Н Н Е
О О С
Э М К
И Л
Й Е
К Д
О Ж
Л
Далее для формирования шифротекста считывают содержимое
таблицы по строкам.
Если шифротекст записывать группами по пять букв, получается
такое шифрованное сообщение:
ПКУТЫ АКИИЛ ОИДВЙ РОЧЙЕ ЛЙАЕА ННЕКД ОГРНГ ООСОЖ
ЦОСНР ЭМКЛ
Объединение букв шифротекста в 5-буквенные группы не входит в ключ
шифра и осуществляется для удобства записи не смыслового текста.

15.

Одиночная перестановка по ключу
15
Несколько большей стойкостью к раскрытию обладает метод
шифрования, называемый одиночной перестановкой
по ключу.
Этот метод отличается от предыдущего тем, что после
заполнения таблицы её столбцы переставляются в
порядке, задаваемом
ключевым словом, фразой или набором чисел;
его длина совпадает с длиной строки таблицы.
После перестановки столбцов таблицы для
формирования шифротекста считывают содержимое
таблицы по строкам.

16.

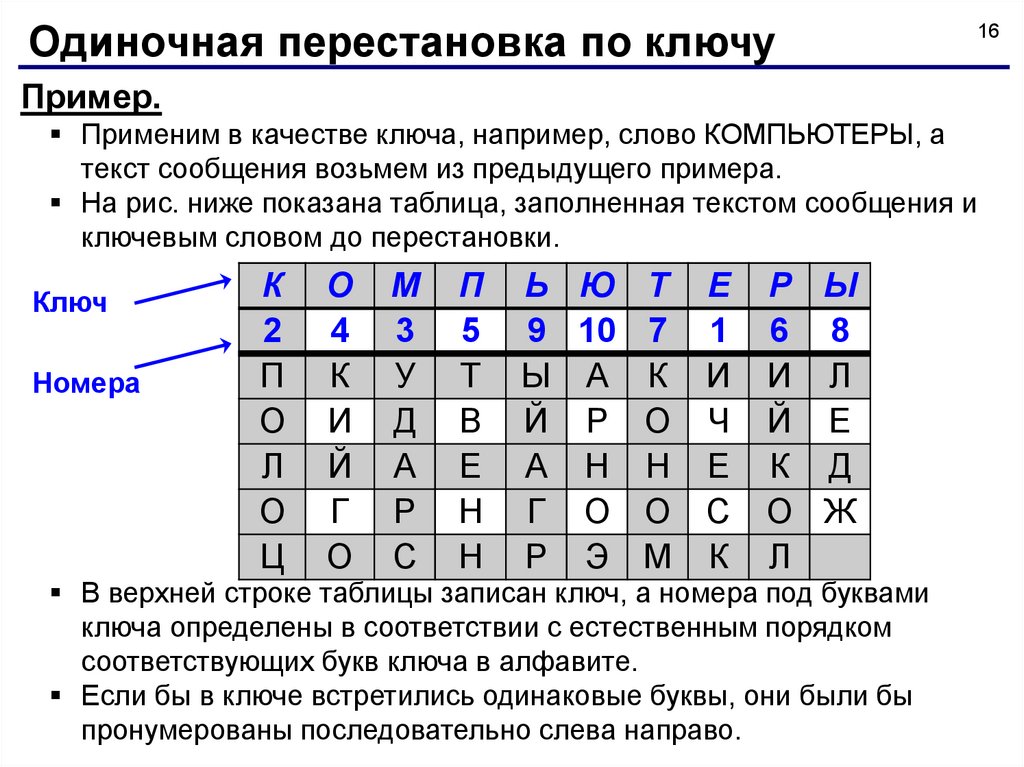
Одиночная перестановка по ключу
16
Пример.
Применим в качестве ключа, например, слово КОМПЬЮТЕРЫ, а
текст сообщения возьмем из предыдущего примера.
На рис. ниже показана таблица, заполненная текстом сообщения и
ключевым словом до перестановки.
Ключ
Номера
К
2
П
О
Л
О
Ц
О
4
К
И
Й
Г
О
М
3
У
Д
А
Р
С
П
5
Т
В
Е
Н
Н
Ь
9
Ы
Й
А
Г
Р
Ю
10
А
Р
Н
О
Э
Т Е
7 1
К И
О Ч
Н Е
О С
М К
Р Ы
6 8
И Л
Й Е
К Д
О Ж
Л
В верхней строке таблицы записан ключ, а номера под буквами
ключа определены в соответствии с естественным порядком
соответствующих букв ключа в алфавите.
Если бы в ключе встретились одинаковые буквы, они были бы
пронумерованы последовательно слева направо.

17.

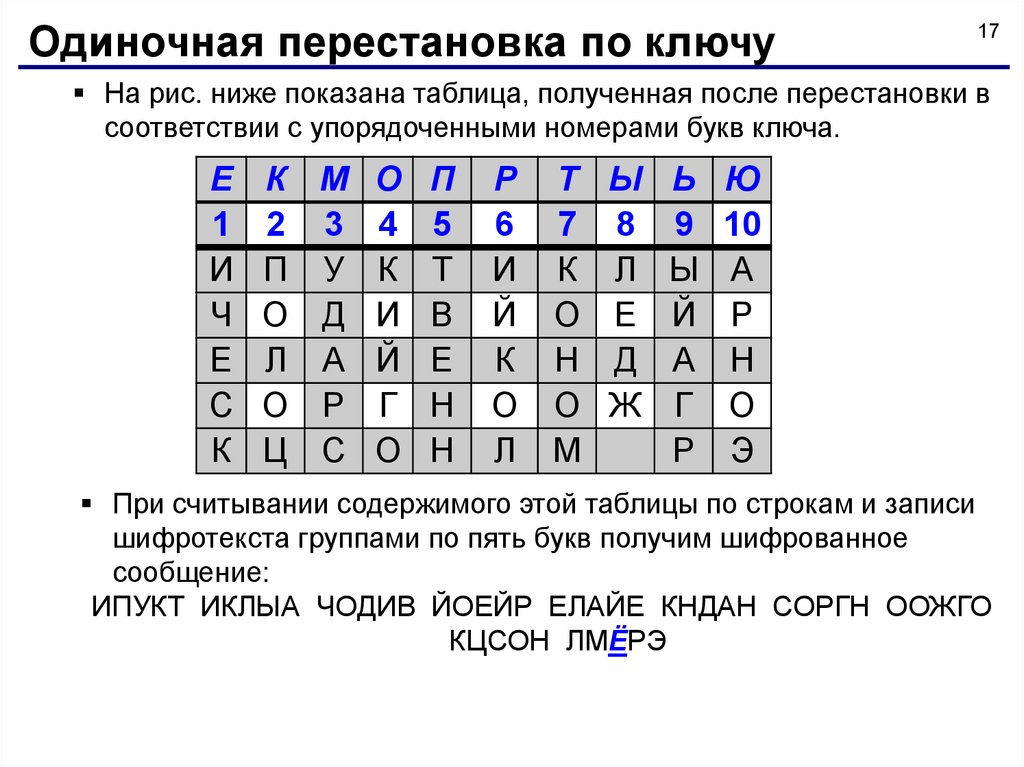
Одиночная перестановка по ключу
17
На рис. ниже показана таблица, полученная после перестановки в
соответствии с упорядоченными номерами букв ключа.
Е
1
И
Ч
Е
С
К
К
2
П
О
Л
О
Ц
М
3
У
Д
А
Р
С
О
4
К
И
Й
Г
О
П
5
Т
В
Е
Н
Н
Р
6
И
Й
К
О
Л
Т
7
К
О
Н
О
М
Ы
8
Л
Е
Д
Ж
Ь
9
Ы
Й
А
Г
Р
Ю
10
А
Р
Н
О
Э
При считывании содержимого этой таблицы по строкам и записи
шифротекста группами по пять букв получим шифрованное
сообщение:
ИПУКТ ИКЛЫА ЧОДИВ ЙОЕЙР ЕЛАЙЕ КНДАН СОРГН ООЖГО
КЦСОН ЛМЁРЭ

18.

Одиночная перестановка по ключу
18
Расшифрование выполняется в следующем порядке.
Подсчитываем число знаков в зашифрованном тексте и
делим на число знаков ключа
49: 10=4 и 9 знаков в остатке,
т.е. получим 4 полных строки и одну неполную.
Под знаками ключа в соответствующей
последовательности записываем горизонтально
(строками) символы зашифрованного текста в
определенном выше количестве:
в строках с 1-й по 4-ю – по 10 символов,
а в последней – 9 символов (9 букв в остатке).
По столбцам таблицы (вертикально) читаем исходный
текст.

19.

Одиночная перестановка по ключу
19
Обрабатываем шифрограмму
ИПУКТ ИКЛЫА ЧОДИВ ЙОЕЙР ЕЛАЙЕ КНДАН СОРГН ООЖГО
КЦСОН ЛМЁРЭ
Берем первые 10 символов и записываем в 1-ю строку
следующим образом:
первую букву, т.е. И в колонку под числом 1;
вторую букву, т.е. П в колонку под числом 2;
третью букву, т.е. У в колонку под числом 3;
четвертую букву, т.е. К в колонку под числом 4;
пятую букву, т.е. У в колонку под числом 5;
шестую букву, т.е. И в колонку под числом 6;
седьмую букву, т.е. К в колонку под числом 7;
восьмую букву, т.е. Л в колонку под числом 8;
девятую букву, т.е. Ы в колонку под числом 9;
десятую букву, т.е. А в колонку под числом 10.
К
2
П
О
4
К
М
3
У
П
5
Т
Ь Ю Т
9 10 7
Ы А К
Е
1
И
Р Ы
6 8
И Л

20.

Одиночная перестановка по ключу
20
ИПУКТ ИКЛЫА ЧОДИВ ЙОЕЙР ЕЛАЙЕ КНДАН СОРГН ООЖГО
КЦСОН ЛМЁРЭ
Берем вторую десятку символов и записываем во 2-ю строку:
первую букву, т.е. Ч в колонку под числом 1;
вторую букву, т.е. О в колонку под числом 2;
третью букву, т.е. Д в колонку под числом 3;
четвертую букву, т.е. И в колонку под числом 4;
пятую букву, т.е. В в колонку под числом 5;
шестую букву, т.е. Й в колонку под числом 6;
седьмую букву, т.е. О в колонку под числом 7;
восьмую букву, т.е. Е в колонку под числом 8;
девятую букву, т.е. Й в колонку под числом 9;
десятую букву, т.е. Р в колонку под числом 10.
К
2
П
О
О
4
К
И
М
3
У
Д
П
5
Т
В
Ь
9
Ы
Й
Ю
10
А
Р
Т
7
К
О
Е
1
И
Ч
Р Ы
6 8
И Л
Й Е

21.

Одиночная перестановка по ключу
21
ИПУКТ ИКЛЫА ЧОДИВ ЙОЕЙР ЕЛАЙЕ КНДАН СОРГН ООЖГО
КЦСОН ЛМЁРЭ
Берем третью десятку символов и записываем в 3-ю строку:
первую букву, т.е. Е в колонку под числом 1;
вторую букву, т.е. Л в колонку под числом 2;
третью букву, т.е. А в колонку под числом 3;
четвертую букву, т.е. Й в колонку под числом 4;
пятую букву, т.е. Е в колонку под числом 5;
шестую букву, т.е. К в колонку под числом 6;
седьмую букву, т.е. Н в колонку под числом 7;
восьмую букву, т.е. Д в колонку под числом 8;
девятую букву, т.е. А в колонку под числом 9;
десятую букву, т.е. Н в колонку под числом 10.
2
П
О
Л
4
К
И
Й
3
У
Д
А
5
Т
В
Е
9
Ы
Й
А
10
А
Р
Н
7
К
О
Н
1
И
Ч
Е
6
И
Й
К
8
Л
Е
Д

22.

Одиночная перестановка по ключу
22
ИПУКТ ИКЛЫА ЧОДИВ ЙОЕЙР ЕЛАЙЕ КНДАН СОРГН ООЖГО
КЦСОН ЛМЁРЭ
Берем четвертую десятку символов и записываем в 4-ю строку:
первую букву, т.е. С в колонку под числом 1;
вторую букву, т.е. О в колонку под числом 2;
третью букву, т.е. Р в колонку под числом 3;
четвертую букву, т.е. Г в колонку под числом 4;
пятую букву, т.е. Н в колонку под числом 5;
шестую букву, т.е. О в колонку под числом 6;
седьмую букву, т.е. О в колонку под числом 7;
восьмую букву, т.е. Ж в колонку под числом 8;
девятую букву, т.е. Г в колонку под числом 9;
десятую букву, т.е. О в колонку под числом 10.
2
П
О
Л
О
4
К
И
Й
Г
3
У
Д
А
Р
5
Т
В
Е
Н
9
Ы
Й
А
Г
10
А
Р
Н
О
7
К
О
Н
О
1
И
Ч
Е
С
6 8
И Л
Й Е
К Д
О Ж

23.

Одиночная перестановка по ключу
23
ИПУКТ ИКЛЫА ЧОДИВ ЙОЕЙР ЕЛАЙЕ КНДАН СОРГН ООЖГО
КЦСОН ЛМЁРЭ
Берем пятую десятку символов и записываем в 5-ю строку:
первую букву, т.е. К в колонку под числом 1;
вторую букву, т.е. Ц в колонку под числом 2;
третью букву, т.е. С в колонку под числом 3;
четвертую букву, т.е. О в колонку под числом 4;
пятую букву, т.е. Н в колонку под числом 5;
шестую букву, т.е. Л в колонку под числом 6;
седьмую букву, т.е. М в колонку под числом 7;
восьмую букву, т.е. Ё в колонку под числом 8;
девятую букву, т.е. Р в колонку под числом 9;
десятую букву, т.е. Э в колонку под числом 10.
2
П
О
Л
О
Ц
4
К
И
Й
Г
О
3
У
Д
А
Р
С
5
Т
В
Е
Н
Н
9 10 7
Ы А К
Й Р О
А Н Н
Г О О
Р Э М
1
И
Ч
Е
С
К
6
И
Й
К
О
Л
8
Л
Е
Д
Ж
Ё

24.

Одиночная перестановка по ключу
2
П
О
Л
О
Ц
4
К
И
Й
Г
О
3
У
Д
А
Р
С
5
Т
В
Е
Н
Н
9 10 7
Ы А К
Й Р О
А Н Н
Г О О
Р Э М
1
И
Ч
Е
С
К
6
И
Й
К
О
Л
24
8
Л
Е
Д
Ж
Ё
Если выписать символы из таблицы по столбцам, получается такое
исходное сообщение:
ПОЛОЦКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНО-ЭКОНОМИЧЕСКИЙ
КОЛЛЕДЖЁ

25.

Двойная перестановка
Для обеспечения дополнительной скрытности можно
повторно зашифровать сообщение, которое уже было
зашифровано. Такой метод шифрования называется
двойной перестановкой.
25

26.

Двойная перестановка
26
В случае двойной перестановки столбцов и строк
таблицы перестановки определяются
отдельно для столбцов
и отдельно для строк.
Сначала в таблицу записывается текст сообщения по
столбцам,
а потом поочередно переставляются столбцы согласно
ключу для столбцов,
а затем строки согласно ключу для строк.
При расшифровывании порядок перестановок должен
быть обратным.
Ключом к шифру служит последовательность номеров
столбцов и номеров строк исходной таблицы при
перестановке.

27.

Двойная перестановка
27
Пример.
Применим в качестве ключа, например, последовательности:
для столбцов – 4 6 10 9 1 3 8 2 7 5,
для строк – 2 4 1 5 3
а текст сообщения возьмем из предыдущего примера.
На рис. ниже показана таблица, заполненная текстом сообщения и
ключами до перестановки.
2
4
1
5
3
4
П
О
Л
О
Ц
6 10 9
К У Т
И Д В
Й А Е
Г Р Н
О С Н
1
Ы
Й
А
Г
Р
3 8 2
А К И
Р О Ч
Н Н Е
О О С
Э М К
7 5
И Л
Й Е
К Д
О Ж
Л

28.

Двойная перестановка
28
На рис. ниже показана таблица, полученная после перестановки в
соответствии со значением ключа по столбцам.
2
4
1
5
3
1
Ы
Й
А
Г
Р
2
И
Ч
Е
С
К
3
А
Р
Н
О
Э
4
П
О
Л
О
Ц
5
Л
Е
Д
Ж
6
К
И
Й
Г
О
7
И
Й
К
О
Л
8
К
О
Н
О
М
9 10
Т У
В Д
Е А
Н Р
Н С

29.

Двойная перестановка
29
На рис. ниже показана таблица, полученная после перестановки в
соответствии со значением ключа по строкам.
1
2
3
4
5
1
А
Ы
Р
Й
Г
2
Е
И
К
Ч
С
3
Н
А
Э
Р
О
4
Л
П
Ц
О
О
5 6 7
Д Й К
Л К И
О Л
Е И Й
Ж Г О
8
Н
К
М
О
О
9 10
Е А
Т У
Н С
В Д
Н Р
При считывании содержимого этой таблицы по строкам и записи
шифротекста группами по пять букв получим шифрованное
сообщение:
АЕНЛД ЙКНЕА ЫИАПЛ КИКТУ РКЭЦЁ ОЛМНС ЙЧРОЕ ИЙОВД
ГСООЖ ГООНР

30.

Двойная перестановка
Число вариантов двойной перестановки быстро возрастает
при увеличении размера таблицы:
для таблицы 3×3 36 вариантов,
для таблицы 4×4 576 вариантов,
для таблицы 5×5 14400 вариантов.
Однако двойная перестановка не отличается высокой
стойкостью и сравнительно просто "взламывается" при
любом размере таблицы шифрования.
30

31.

Магический квадрат
31
Особенности структуры таблицы используются в качестве
ключевой информации в магических квадратах, которые
также применялись в средние века.
Магическими квадратами называют квадратные таблицы
с вписанными в их клетки последовательными
натуральными числами, начиная от 1, которые дают в
сумме по каждому столбцу, каждой строке и каждой
диагонали одно и то же число.
Шифруемый текст вписывали в магические квадраты в
соответствии с нумерацией их клеток.
Если затем выписать содержимое такой таблицы по
строкам, то получится шифротекст, сформированный
благодаря перестановке букв исходного сообщения.
В те времена считалось, что созданные с помощью магических
квадратов шифртексты охраняет не только ключ, но и магическая
сила.

32.

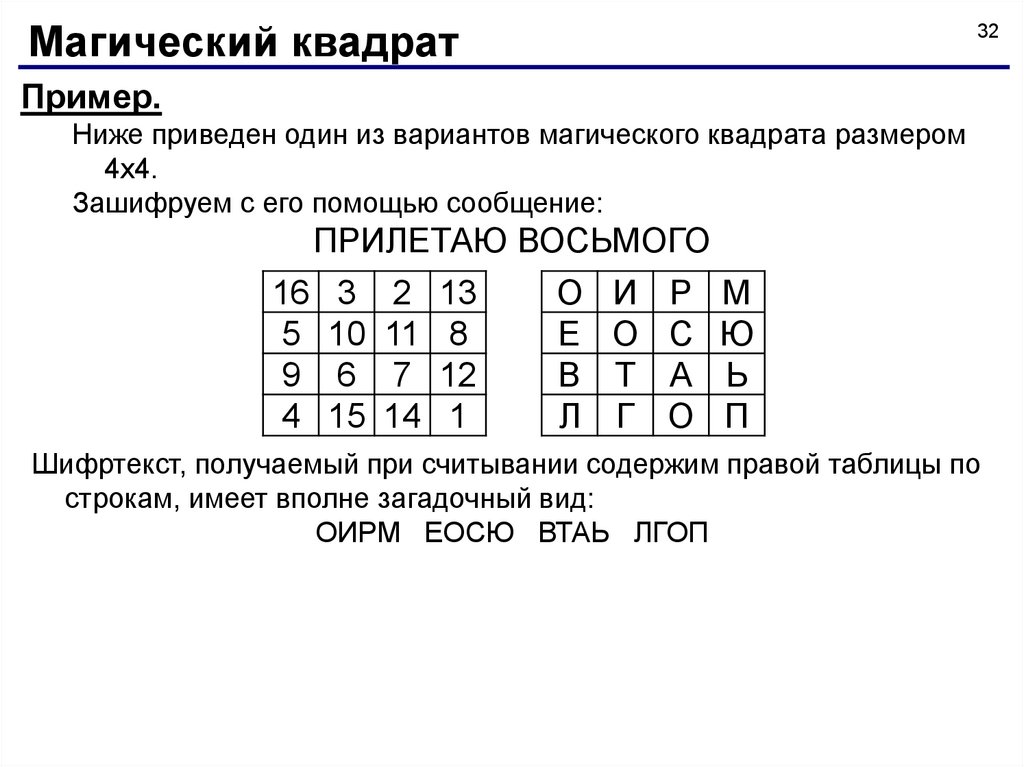
Магический квадрат
32
Пример.
Ниже приведен один из вариантов магического квадрата размером
4х4.
Зашифруем с его помощью сообщение:
ПРИЛЕТАЮ ВОСЬМОГО
16 3 2 13
5 10 11 8
9 6 7 12
4 15 14 1
О
Е
В
Л
И
О
Т
Г
Р
С
А
О
М
Ю
Ь
П
Шифртекст, получаемый при считывании содержим правой таблицы по
строкам, имеет вполне загадочный вид:
ОИРМ ЕОСЮ ВТАЬ ЛГОП

33.

Магический квадрат
33
Число магических квадратов быстро возрастает с
увеличением размера квадрата.
Существует только один магический квадрат размером
3×3 (если не учитывать его повороты).
Количество магических квадратов 4×4 составляет уже
880,
а количество магических квадратов 5×5 – около
250000.
Магические квадраты средних и больших размеров могли
служить хорошей базой для обеспечения нужд
шифрования того времени,
т.к. практически нереально выполнить вручную пepeбop
всех вариантов для такого шифра.

34.

Магический квадрат
Особенности структуры таблицы используются в качестве
ключевой информации в магических квадратах, которые
также применялись в средние века.
34

35.

Шифр Кардано
35
К шифрам перестановки относится и шифр Кардано.
В середине ХVI века итальянским математиком
Кардано была выдвинута идея использования части
самого передаваемого открытого текста в качестве
ключа и новый способ шифрования, получивший
название «решетка Кардано».
Для ее изготовления берется квадратный кусок
картона, в котором по специальным правилам
прорезаются «окна».
При шифровании решетка накладывалась на лист
бумаги, и открытый текст вписывался в окна.
Затем решетка поворачивалась на 90 градусов, и вновь
вписывался текст, всего 4 раза.

36.

Шифр Кардано
36
Главное требование к «решетке Кардано» – при всех
поворотах окна не должны попадать на одно и то же
место бумаги.
Пустые места заполнялись произвольными буквами.
Затем шифрограмма выписывалась построчно.
Решетка Кардано позволяет осуществлять перестановку
букв достаточно быстро.
Как математик, Кардано сумел вычислить количество
квадратов-решеток (ключей) заданного размера NxN.
Если N – четное число, то это количество равно 4
При N=10 оно имеет порядок 1015.
N 2 1
.

37.

37
2. Стеганографические шифры

38.

Шифр Ришелье
Идея шифра-решетки, предложенного Кардано, лежит и в
основе знаменитого шифра Ришелье, в котором
шифрованный текст внешне имел вид осмысленного
сообщения, не имеющего никого отношения к
передаваемой информации.
Из плотного материала вырезался прямоугольник
размером, например, 7×10;
в нем проделывались окна (на рисунке они
заштрихованы).
I
.
L O V E
.
Y O U
I
.
H A V E
.
Y O U
D E E P
.
U N D E R
M Y
.
S K
I
N . M Y
L O V E
.
L A S T S
F O R E V E R .
I
N
H Y P E R S P A С E
38

39.

Шифр Ришелье
39
I
.
L O V E
.
Y O U
I
.
H A V E
.
Y O U
D E E P
.
U N D E R
M Y
.
S K
I
N . M Y
L O V E
.
L A S T S
F O R E V E R .
I
N
H Y P E R S P A С E
Секретный текст вписывался в эти окна,
затем решетка снималась
и оставшиеся клетки заполнялись так, чтобы получалось
сообщение, имеющее совсем другой смысл.
Суровую команду на английском языке:
«YOU KILL AT ONCE»
с помощью такой решетки можно спрятать в «невинный» текст
любовного содержания:
«I LOVE YOU. I HAVE YOU. DEEP UNDER MY SKIN. MY LOVE. LASTS
FOREVER. IN HYPERSPACE».

40.

Шифр Ришелье
40
Такого рода шифр использовал известный русский писатель и дипломат
А.С.Грибоедов.
Будучи послом в Персии, он писал своей жене «невинные»
послания,
которые, попав в руки жандармерии, для которой и были
предназначены, дешифровывались по соответствующей
«решетке»
и передавались царскому правительству уже как секретные
сведения.

41.

Шифр Ришелье
41
Такие шифры относятся уже к стеганографическим
методам защиты информации, которые предполагают
сокрытие самого факта передачи информации.
К ним относятся также не имеющие отношения к
криптографии тайнопись (невидимые чернила,
проявляющиеся при специальной обработке, микроточки в
тексте книги и т.п.).
Стеганографические методы в виде замаскированных
закладок используются для защиты программных
продуктов от несанкционированного копирования.