10.95M

Category: $mathematics$ mathematics

Решение комбинаторных задач в начальной школе

2.

«Решение
комбинаторных задач
в начальной школе»
КГУ «ОШ №17» г.Темиртау
Давлетшина Г.В.
Ильясова А.М.

Цели: обмен опытом применения методов решения
комбинаторных задач в начальной школе
Задачи:
• раскрыть значение решения комбинаторных задач в
развитии и обучении учащихся на уроках математики,
• совместная отработка методических подходов,
• развивать интерес к оригинальным образовательным
технологиям,
• вызвать желание к сотрудничеству и взаимодействию.
Ожидаемый результат: участники мастер-класса
получат возможность ознакомиться с предлагаемыми
способами работы с комбинаторными задачами, примут
активное участие в решении данных заданий и смогут
применять методы решения комбинаторных задач на
практике.

4.

• Ты попал в волшебный лес. Выбраться
можно только через эти двери.
Но домой вернётся тот, у кого хорошая
логика. За первой дверью горит
волшебный огонь. Как только попадёшь,
то сгоришь. За второй дверью
кромешная темнота. За третьей дверью
голодный монстр. Как ты будешь
возвращаться домой?
Ответ: в лесу можно найти палку, зажечь от
огня факел и выйти в дверь «Темнота»

5.

Ответ: 58

6.

Шли гуси на водопой. Один вслед за другим.
Один гусь посмотрел вперед, перед ним 10
голов. Посмотрел назад, за ним 22 лапы.
Сколько гусей шло на водопой?
Ответ: 22

7.

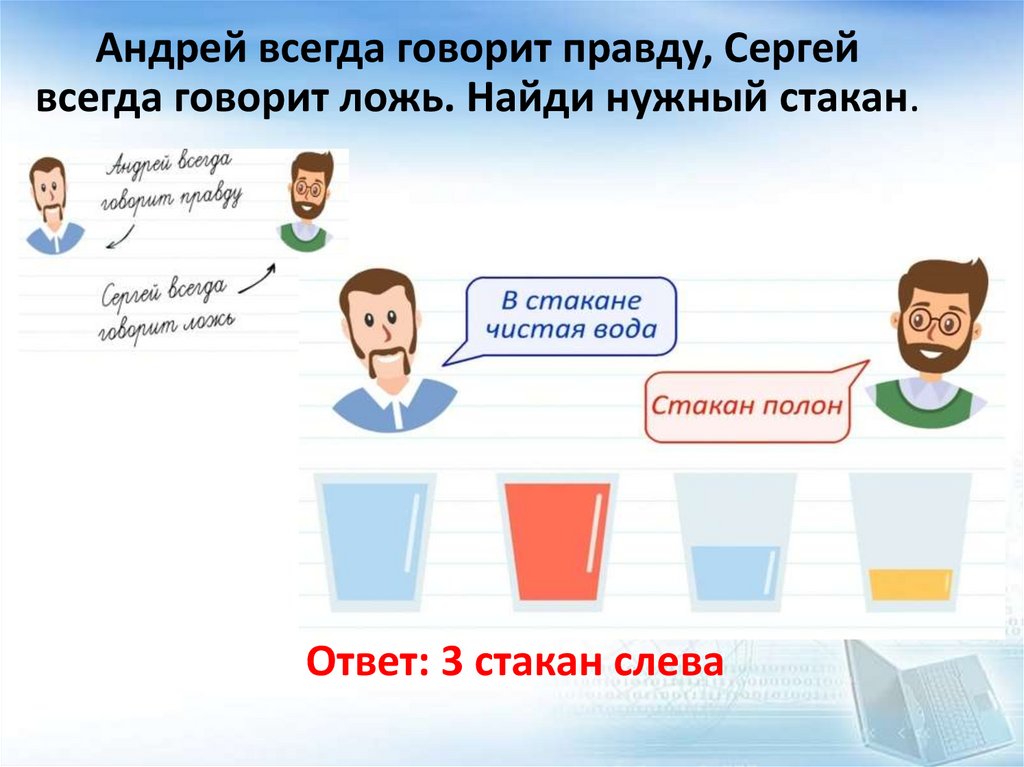
Андрей всегда говорит правду, Сергей
всегда говорит ложь. Найди нужный стакан.
Ответ: 3 стакан слева

8.

Ответ: на 1 этаж

9.

Кто может поднять и передвинуть
и коня, и слона?
Ответ: шахматист

10.

«Прямо поедешь – голову
сложишь, направо поедешь –
коня потеряешь, налево
поедешь – меча лишишься»

11.

Что такое комбинаторика и
комбинаторные задачи?
Термин «комбинаторика» происходит от латинского
слова «combina», что в переводе на русский означает –
«сочетать», «соединять».
Термин «комбинаторика»
был введён в
математический обиход
немецким философом,
математиком Лейбницем,
который в 1666 году
опубликовал свой труд
«Рассуждения о
комбинаторном искусстве».

12.

Области применения
комбинаторики:
учебные заведения ( составление расписаний);
сфера общественного питания (составление меню);
агротехника (размещение посевов на полях);
география (раскраска карт);
биология (расшифровка кода ДНК);
лингвистика (рассмотрение вариантов комбинаций букв);
спортивные соревнования (расчёт количества игр между
участниками);
химия (анализ возможных связей между химическими
элементами);
экономика (анализ вариантов купли-продажи акций);
доставка почты (рассмотрение вариантов пересылки);
военное дело (расположение подразделений).

13.

Способы решения
комбинаторных задач:
методом перебора;
с помощью дерева возможных вариантов;
с помощью таблиц;
с помощью графов;
с помощью комбинаторного правила
умножения.

14.

Решение задачи способом перебора
возможных вариантов
У Ирины 5 подруг: Вера, Зоя, Марина, Полина и
Светлана. Она решила двух из них пригласить в
кино. Укажите все возможные варианты выбора
подруг. Сколько таких вариантов?
Замечание. При решении для краткости будем
писать первые буквы имен.

15.

Решение Вера Зоя Марина Полина Света
Составим сначала все пары, в которые входит
Вера.
ВЗ, ВМ, ВП, ВС - 4 пары
Выпишем теперь пары, в которые входит Зоя, но
не входит Вера.
ЗМ, ЗП, ЗС – 3 пары
Далее составим пары, в которые входит Марина,
но не входят Вера и Зоя.
МП, МС – 2 пары
Далее составим пары, в которые входит Полина.
ПС – 1 пара
Всего существует 4+3+2+1=10
Ответ: 10 вариантов

16.

Рассмотрим ещё одну задачу.
На цветочной клумбе сидели шмель, жук,
бабочка и муха. Два насекомых улетели. Какие
пары насекомых могли улететь? Укажите все
возможные варианты. Сколько таких
вариантов?
Ш
М
Ж
Б

17.

Решение:
Ш
Ж
Ж
Ш
Б
Ж
Ш
М
Всего 3+2+1=6
Ответ: 6 вариантов
Б
Б
М
М

18.

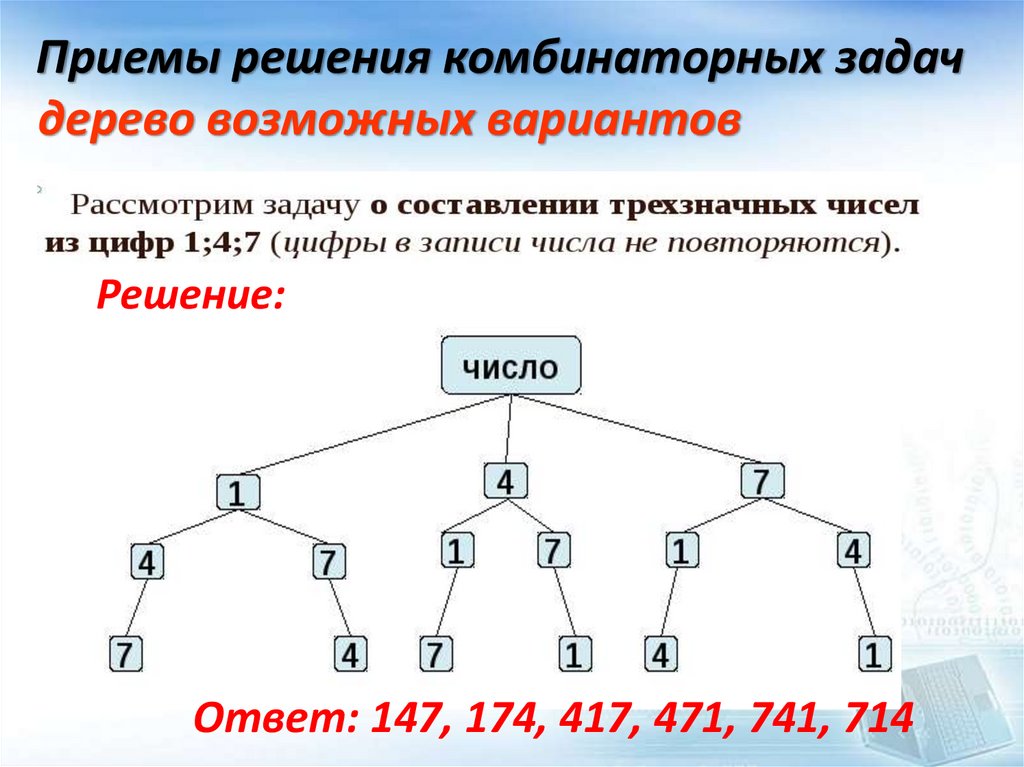
Приемы решения комбинаторных задач
дерево возможных вариантов
Решение:
Ответ: 147, 174, 417, 471, 741, 714

19.

В класс пришли четыре новых ученика Миша,
Катя, Вася, Лиза. С помощью дерева возможных
вариантов покажи, все возможные варианты
расположения четырех учеников за одной партой.
Сколько вариантов выбора будет?
М
К
В
Л

20.

Решение
М
К
Ответ: 12 вариантов
В
Л

21.

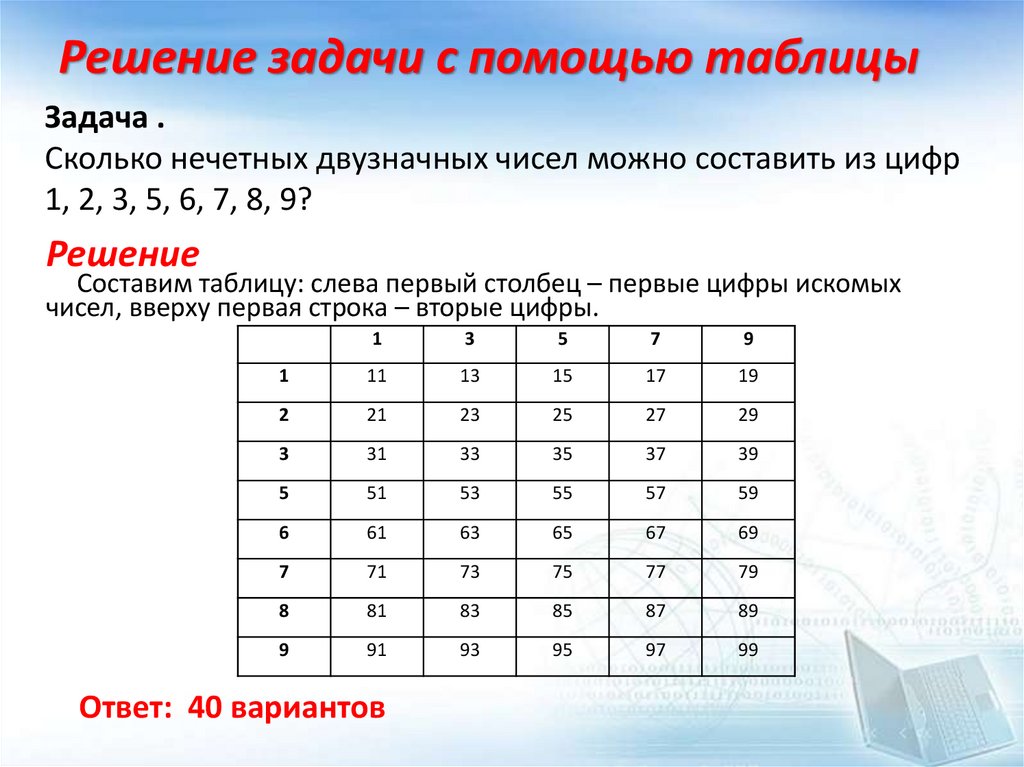
Решение задачи с помощью таблицы
Задача .
Сколько нечетных двузначных чисел можно составить из цифр
1, 2, 3, 5, 6, 7, 8, 9?
Решение
Составим таблицу: слева первый столбец – первые цифры искомых
чисел, вверху первая строка – вторые цифры.
1
3
5
7
9
1
11
13
15
17
19
2
21
23
25
27
29
3
31
33
35
37
39
5
51
53
55
57
59
6
61
63
65
67
69
7
71
73
75
77
79
8
81
83
85
87
89
9
91
93
95
97
99
Ответ: 40 вариантов

22.

Решение задачи с помощью графов
ГРАФ – совокупность объектов со связями между ними. Объекты
представляются как вершины, или узлы графа, а связи – как дуги,
или ребра.
На шахматном турнире принимали участие 7
школьников. Известно, что Павел сыграл шесть
партий, Марина –пять, Лена и Федя-по три ,
Игорь и Денис – по две, Алиса –одну. С кем из
участников турнира играла Лена?

23.

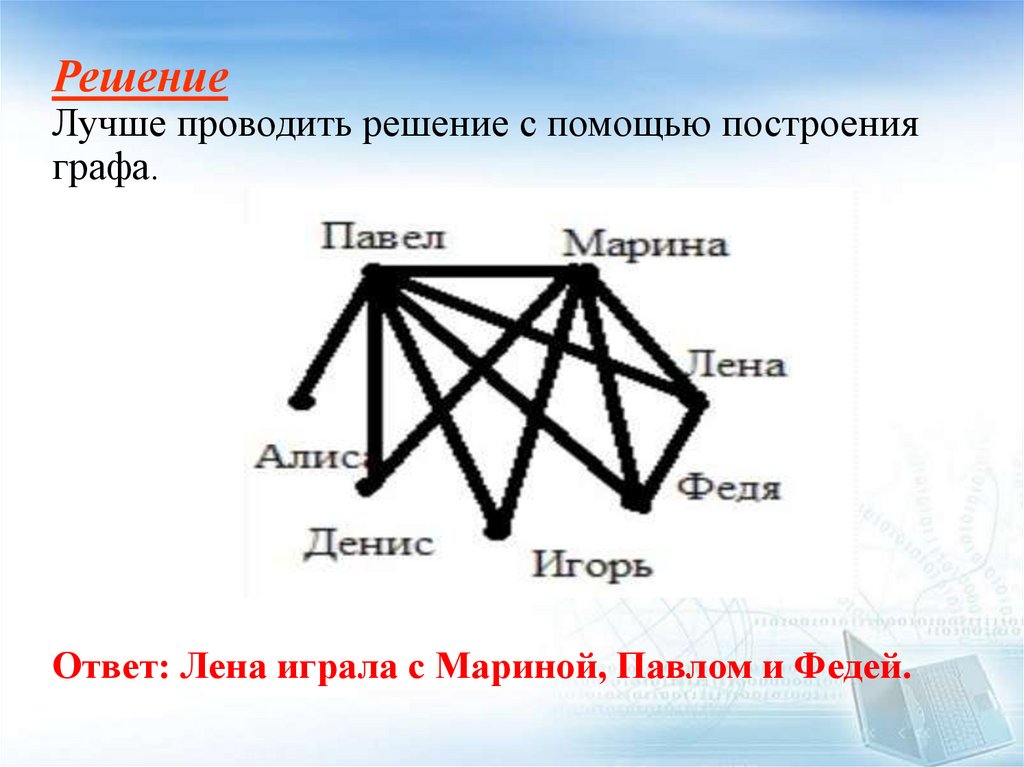
Решение
Лучше проводить решение с помощью построения
графа.
Ответ: Лена играла с Мариной, Павлом и Федей.

24.

Комбинаторное правило умножения

25.

У Куклы Светы 3 юбки и 5 кофт, удачно
сочетающихся по цвету. Сколько различных
комбинаций одежды имеется у Светы?
Решение: 3·5 = 15
26

26.

Работа в группах
1. Реши задачу с помощью комбинаторного правила
умножения.
Сколько различных трёхзначных чисел можно составить из
цифр 1, 2, 3, 4, 5 и 6, используя каждую из цифр ровно по
одному разу.
Ответ: 6 · 5 · 4 = 120

27.

2. Реши задачу с помощью графа.
Пять финалистов конкурса «Алтын сақа» решили
обменяться впечатлениями о конкурсе и позвонили между
собой. Сколько будет сделано звонков?
Ответ: 10 звонков (4+3+2+1=10)

28.

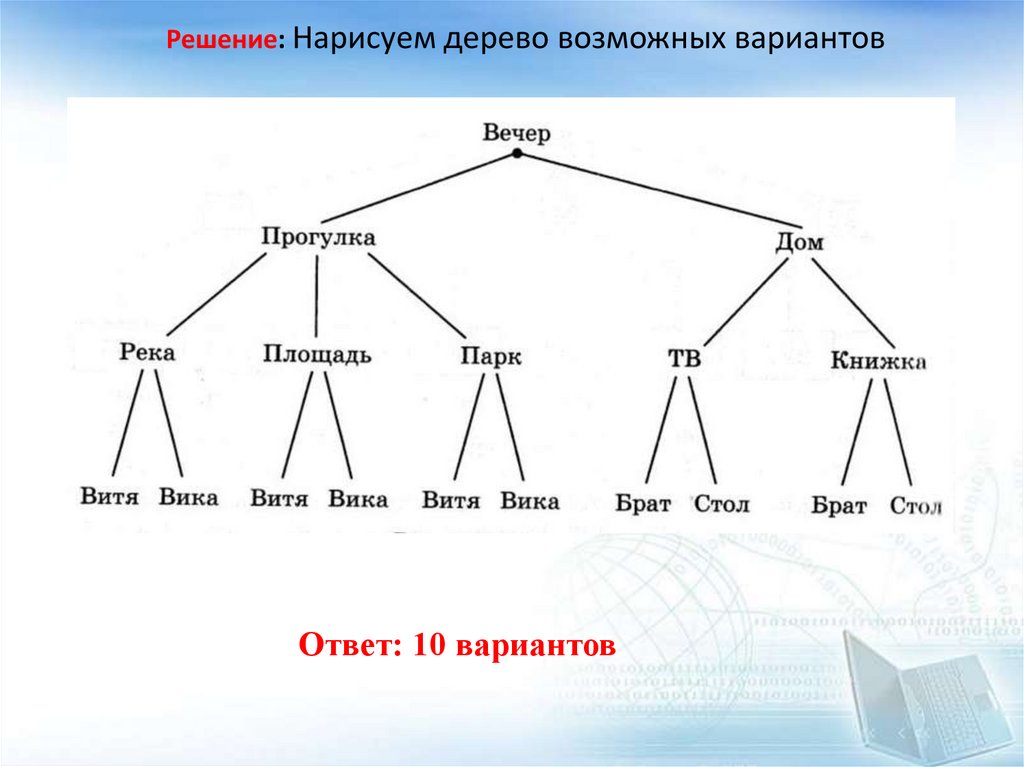
3. Реши задачу с помощью дерева возможных вариантов.
«Этот вечер свободный можно так
провести…»: пойти погулять к реке,
на площадь или в парк и потом пойти
в гости к Вове или к Вике. А можно
остаться дома, сначала посмотреть
телевизор или почитать книжку, а
потом поиграть с братом, или
разобрать наконец у себя на
письменном столе.
Посчитайте, сколько возможно
вариантов провести свободный вечер.
.

29.

Решение: Нарисуем дерево возможных вариантов
Ответ: 10 вариантов

30.

4. Реши задачу с помощью метода перебора.
В 4 «Б» классе в среду 4 урока: математика, русский язык,
английский язык, цифровая грамотность. Сколько можно
составить вариантов расписания на среду?
Ответ: 24 варианта

31.

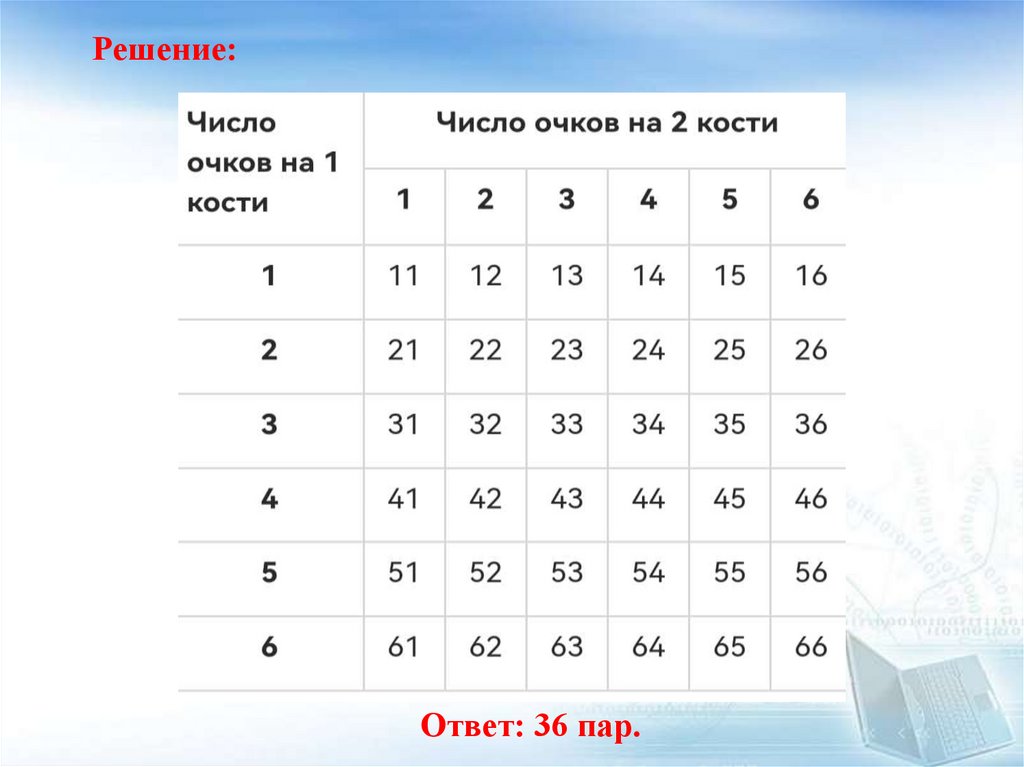
5. Реши задачу с помощью таблицы.
Бросаются две игральные кости. Сколько различных пар
очков может появиться на верхних гранях костей?

32.

Решение:
Ответ: 36 пар.

33.

6. Реши задачу с помощью дерева возможных вариантов.
В каком году родился старик Хоттабыч, если он
утверждает, что записать год его рождения можно
трёхзначным числом, используя цифры 3,9,5.
И если отнять от числа сотен число десятков, а
потом прибавить число единиц, то получится 7
(цифры не повторяются).

34.

Решение:
3
395
9
359
935
5
953
593
538
Исключаем варианты с числом сотен 3, а
потом по дереву выполняем нужные вычисления.
Ответ: 953
проверка: 953= 9 – 5 +3 = 7

35.

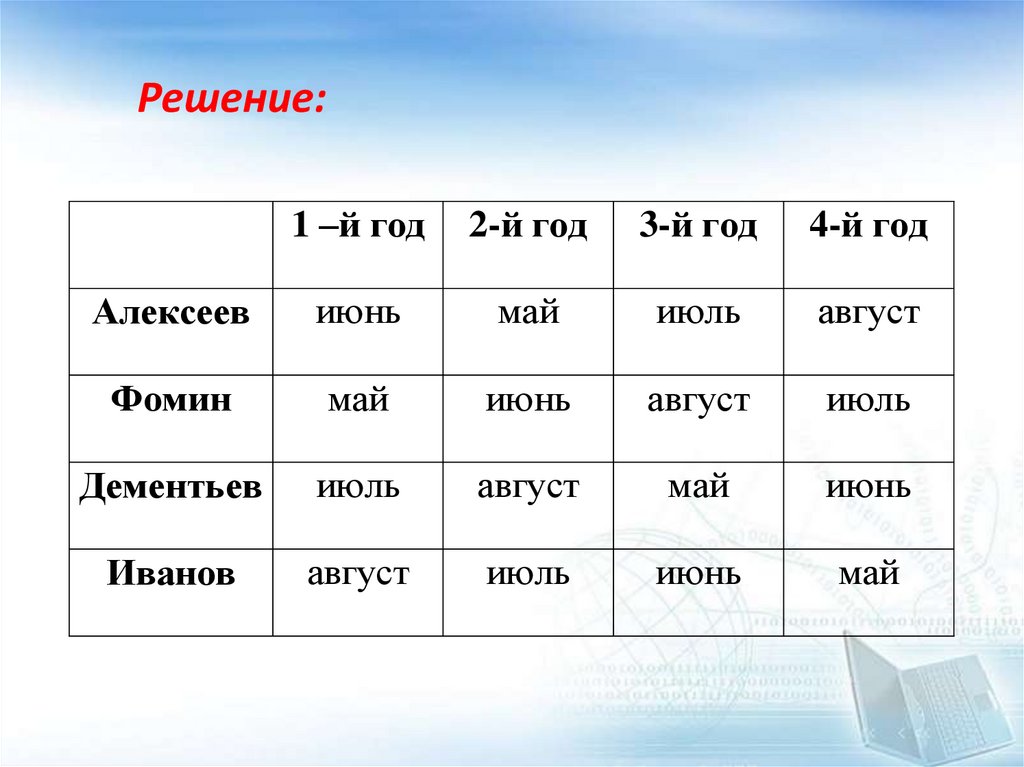
В течение последних четырех лет Алексеев, Фомин,
Дементьев и Иванов получали очередной отпуск в
мае, июне, июле или в августе. Причем, если один
из них отдыхал в мае, то другой - в июне, третий – в
июле, а четвертый – в августе. Каждый их них
получал отпуск в эти четыре года в разные месяцы.
Так в первый год Дементьев отдыхал в июле, во
второй год – в августе. Алексеев во второй год
отдыхал в мае, Иванов в третий год – в июне, а
Фомин в четвертый год – в июле.
Кто в каком месяце отдыхал в каждом из этих четырех лет?

36.

Решение:
1 –й год
2-й год
3-й год
4-й год
Алексеев
июнь
май
июль
август
Фомин
май
июнь
август
июль
Дементьев
июль
август
май
июнь
Иванов
август
июль
июнь
май

37.

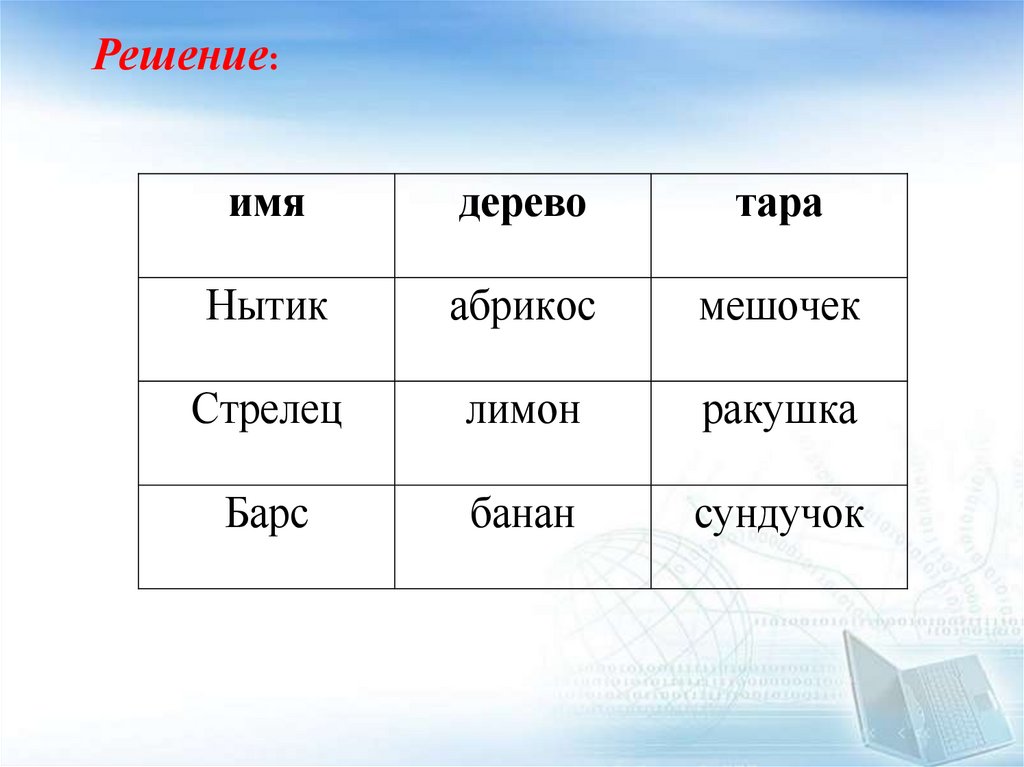
Три пирата: Нытик, Стрелец и Барс зарыли свои сокровища
на одном острове. Один из них зарыл возле дерева
лимона, другой – банана, а третий – абрикоса. Ёмкость
для хранения тоже у каждого была своя: один
использовал сундучок, второй – большую морскую
ракушку, а третий – кожаный мешочек.
• Определите имя пирата, а также где и чем хранил
свои сокровища каждый из них, если известно, что:
• Ракушку использовал не Нытик.
• Тот, кто закопал сокровища под абрикосом, использовал
мешочек.
• Барс закопал сундучок, но не под лимоном.