Лекция 6 Переходные процессы в RL и RC цепях (1)

1. Лекция 6 Переходные процессы в RL и RC цепях

1 Переходные процессы в RL цепях
2 Переходные процессы в RC цепях
1. Литература: Горбунов А.Н. и др.
Теоретические основы электротехники. С.248260.

2. Короткое замыкание цепи RL

Требуется определить закон изменения тока
в ветви с катушкой и напряжения на ней
после коммутации.
Выразим переходный
ток через катушку в виде суммы установившейся
и свободной составляющих:
(*)
После коммутации в контуре R, L нет источника, то установившаяся составляющая тока
(**)
По второму закону Кирхгофа:
Характеристическое уравнение имеет вид:
Общее решение для свободной составляющей:
- корень характеристического уравнения.
(***)

3.

Для определения постоянной интегрирования воспользуемся начальным
условием при t = 0:
С учетом (*…***) получим:
Переходный ток:
- постоянная времени цепи.
Постоянная времени - время, в течение которого свободная составляющая
процесса уменьшается в е = 2,72 раз по сравнению с начальным значением.

4.

Выводы
1) При коротком замыкании цепи RL ток
меняется о экспоненциальному закону,
уменьшаясь от начального значения до нуля.
2) Скорость изменения тока определяется
постоянной времени цепи, которая равна
индуктивности катушки, деленной на активное
сопротивление контура
3) Переходный процесс заканчивается t 5 .
4) Напряжение на индуктивности в начальный
момент времени равно напряжению на
активном сопротивлении:

5.

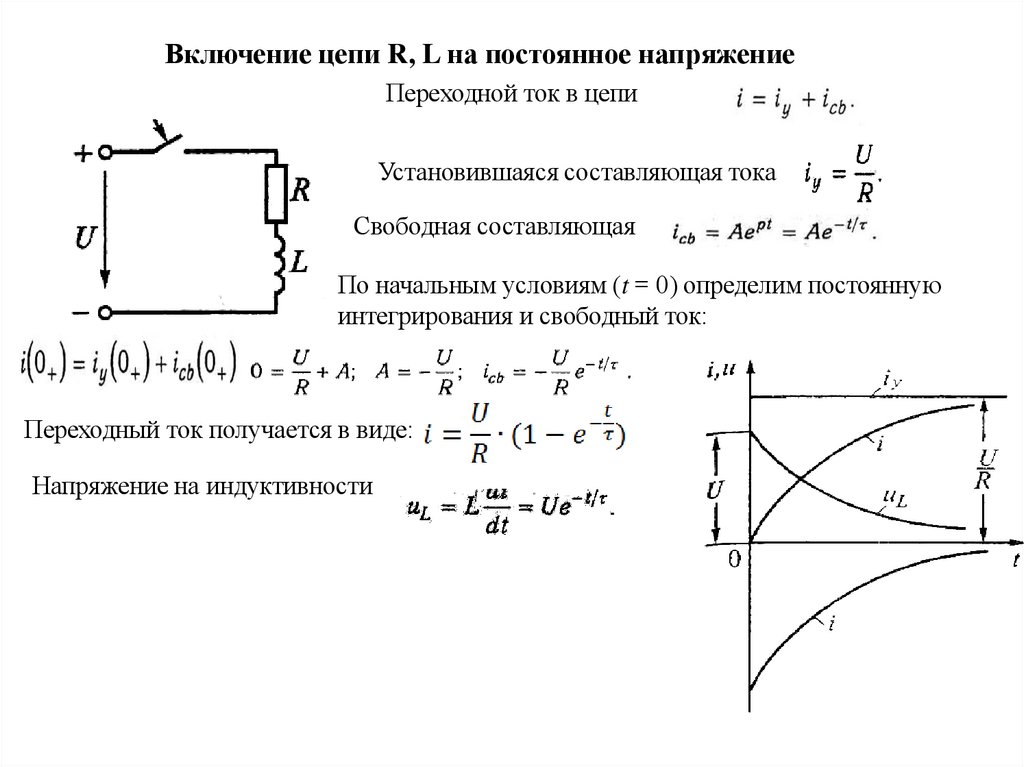
Включение цепи R, L на постоянное напряжение
Переходной ток в цепи
Установившаяся составляющая тока
Свободная составляющая
По начальным условиям (t = 0) определим постоянную
интегрирования и свободный ток:
Переходный ток получается в виде:
Напряжение на индуктивности

6.

Включение цепи R, L на синусоидальное напряжение
Напряжение источника в момент включения:
Установившийся ток
- модуль полного сопротивления цепи.
- сдвиг фаз между напряжением и током
Ψ - начальная фаза тока
Свободный ток определяется
Переходный ток
Используя независимые начальные условия при t = 0
получим постоянную интегрирования
Тогда переходной ток

7.

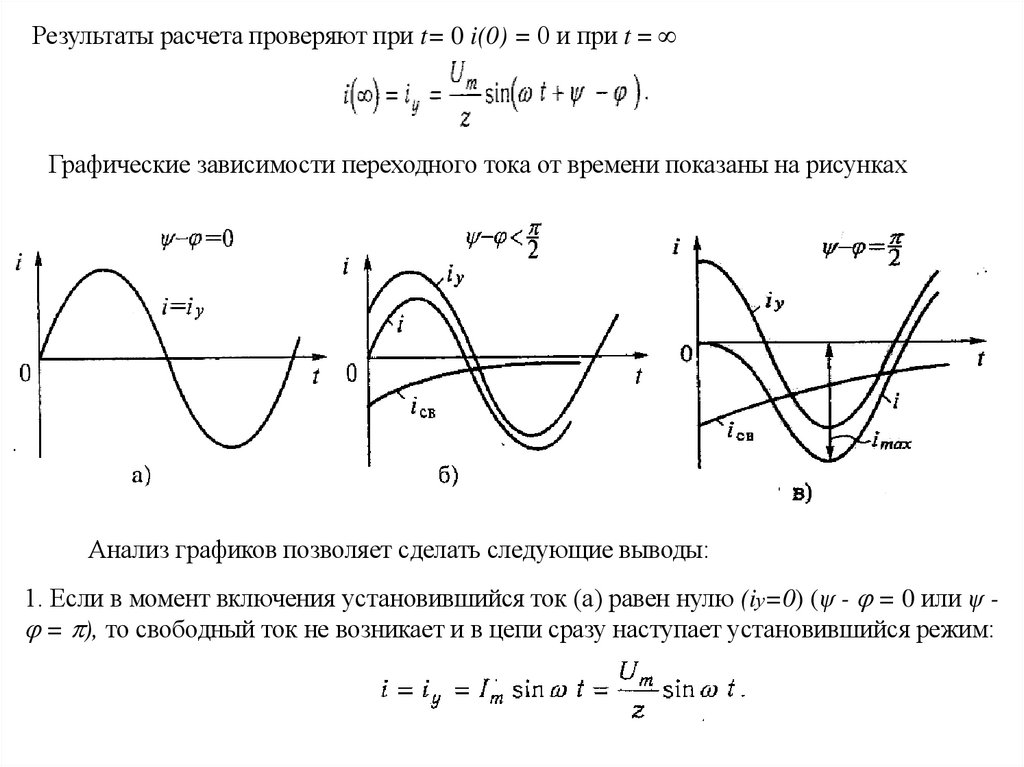
Результаты расчета проверяют при t= 0 i(0) = 0 и при t =
Графические зависимости переходного тока от времени показаны на рисунках
Анализ графиков позволяет сделать следующие выводы:
1. Если в момент включения установившийся ток (а) равен нулю (iу=0) (ψ - = 0 или ψ = ), то свободный ток не возникает и в цепи сразу наступает установившийся режим:

8.

2. Если в момент включения установившийся ток имеет наибольшее значение
(ψ - = /2), то переходный ток достигает максимального значения через
половину периода, однако ни при каких условиях он не может превышать
удвоенной амплитуды установившегося тока.
3. При достаточно большой постоянной времени цепи ток получается
наибольшим, если в момент включения напряжение проходит через нулевое
значение.

9.

Переходные процессы в цепи RС
а) Короткое замыкание цепи R С (разряд конденсатора на резистор)
Рассмотрим переходный процесс при коротком
замыкании цепи конденсатор-резистор, если
предварительно конденсатор заряжен до напряжения
Uc(0+) = U0 = E, iу = 0, Uсу = 0.
Законы Кирхгофа для свободных составляющих
Характеристическое уравнение имеет вид:
Общее решение для свободной составляющей напряжения
где А = U0 - постоянная интегрирования;
= RC - постоянная времени цепи.
Напряжение на конденсаторе:
Переходный ток в цепи:

10.

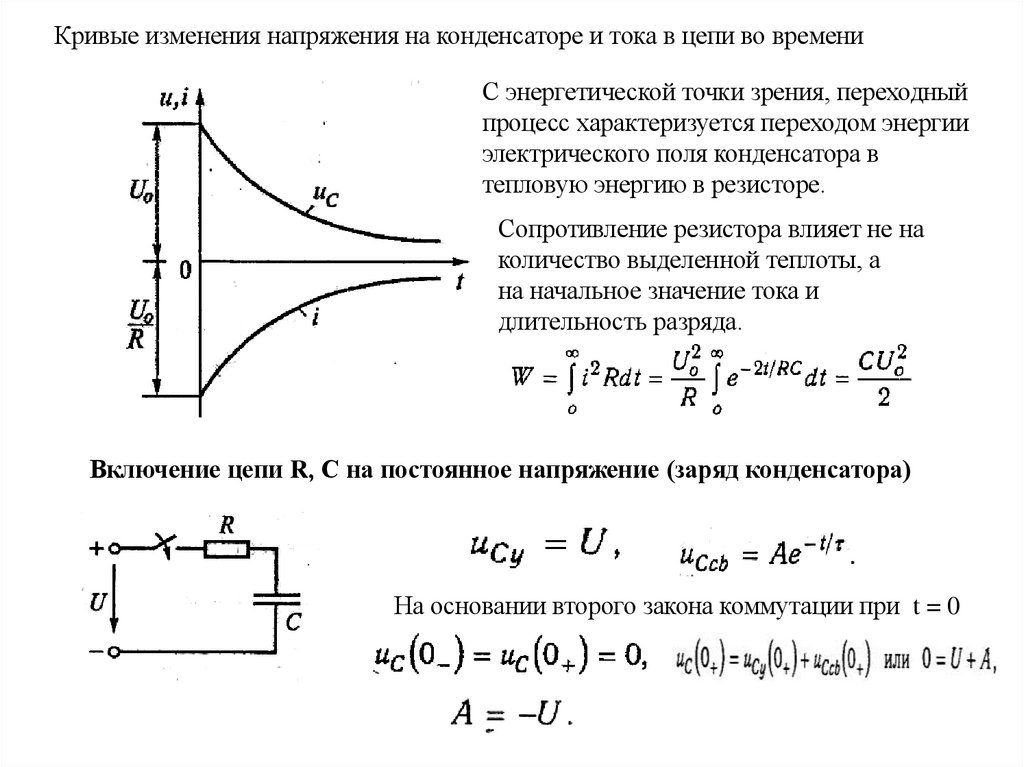
Кривые изменения напряжения на конденсаторе и тока в цепи во времени
С энергетической точки зрения, переходный
процесс характеризуется переходом энергии
электрического поля конденсатора в
тепловую энергию в резисторе.
Сопротивление резистора влияет не на
количество выделенной теплоты, а
на начальное значение тока и
длительность разряда.
Включение цепи R, С на постоянное напряжение (заряд конденсатора)
На основании второго закона коммутации при t = 0

11.

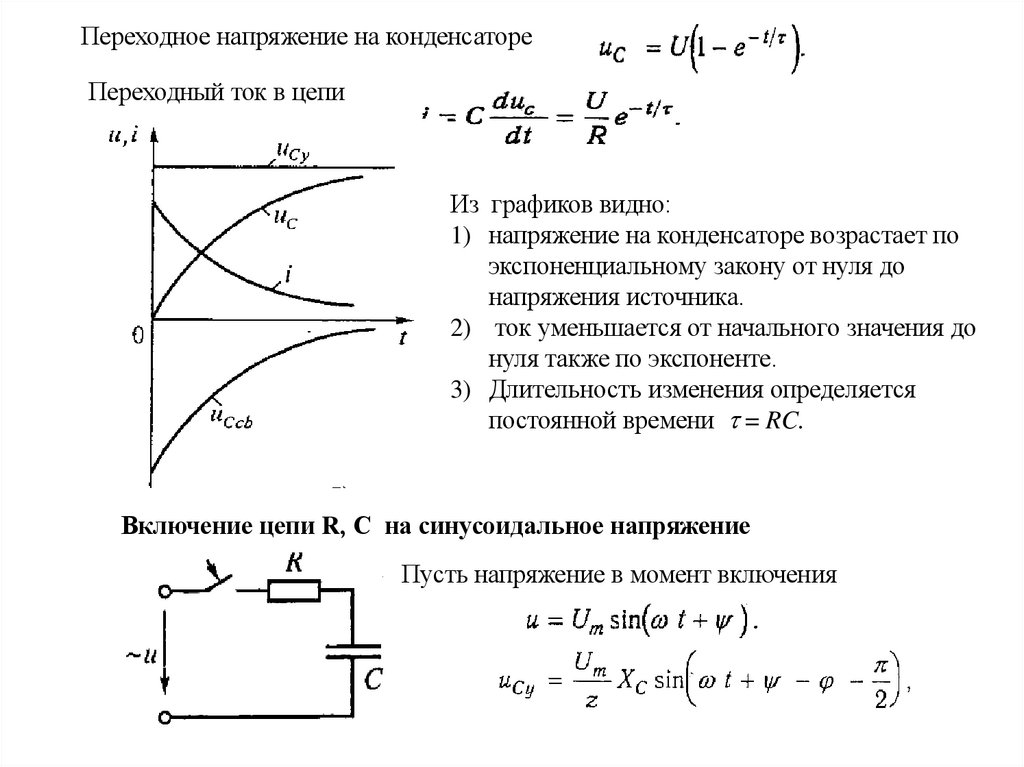
Переходное напряжение на конденсаторе
Переходный ток в цепи
Из графиков видно:
1) напряжение на конденсаторе возрастает по
экспоненциальному закону от нуля до
напряжения источника.
2) ток уменьшается от начального значения до
нуля также по экспоненте.
3) Длительность изменения определяется
постоянной времени = RC.
Включение цепи R, С на синусоидальное напряжение
Пусть напряжение в момент включения

12.

Свободная составляющая напряжения на конденсаторе
Переходное напряжение на конденсаторе
С учетом начальных условий
Окончательное выражение для переходного напряжения на конденсаторе

13.

Переходный ток в цепи
Графические зависимости переходного напряжения на конденсаторе
Выводы:
1. Если в момент включения установившееся напряжение на конденсаторе (а) равно
нулю (ψ - - /2 =0), то свободное напряжение равно нулю. В цепи сразу наступает
установившийся режим.
Если в момент включения установившееся напряжение ( в) имеет наибольшее
значение (ψ - - /2 = /2 ), то переходное напряжение достигает максимального
значения через половину периода и может приблизиться к уд. военной амплитуде
установившегося напряжения, но не превысит его.