Similar presentations:
Лекция Случайная величина. Распределение вероятностей. Диаграмма распределения
1. Случайная величина и ее виды
Одним из важнейших понятий теории вероятностейявляется понятие случайной величины.
В разделе «Случайные события» приводились события,
состоящие в появлении того или иного числа.
Например, при бросании игральной кости могли появится
числа 1, 2, 3, 4, 5 и 6. Наперед определить число
выпавших очков невозможно, поскольку оно зависит от
многих случайных причин, которые полностью не могут
быть учтены. В этом смысле число очков есть величина
случайная; числа 1, 2, 3, 4, 5 и 6 есть возможные
значения этой величины.
Составитель: Самойлова О.А.
2.
Определение: Случайной величиной (СВ) называетсявеличина, которая в результате опыта принимается одно
и только одно значение, причем заранее неизвестно,
какое именно.
Случайная величина связана со случайным событием.
Если случайное событие - это качественная
характеристика испытания, то случайная величина - его
количественная характеристика.
Если при этом события независимы, то и
соответствующие случайные величины также
независимы.
Составитель: Самойлова О.А.
3.
Примеры случайных величин:1) Число родившихся мальчиков среди ста новорожденных
есть случайная величина, которая имеет следующие
возможные значения: 0, 1, 2, …100.
2) Расстояние, которое пролетит снаряд при выстреле из
орудия, есть случайная величина. Действительно,
расстояние зависит не только от установки прицела, но
и от многих других причин (силы и направления ветра,
температуры и т.д.), которые не могут быть полностью
учтены. Возможные значения этой величины
принадлежат некоторому промежутку
a, b .
Составитель: Самойлова О.А.
4.
Случайные величины обозначаются прописнымибуквами X , Y , Z , а их возможные значения –
соответствующими прописными буквами x, y, z.
Например, если случайная величина X имеет три
возможных значения, то они будут обозначены так: x1 , x2 , x3 .
Вероятность того, что случайная величина X примет
значение, равное x1 ; или значение x2 , обозначают через
p1 , p2 и т.д., так что P( X x1 ) p1; P( X x2 ) p2 и т.д.
Составитель: Самойлова О.А.
5.
Случайные величиныДискретные
Непрерывные
Составитель: Самойлова О.А.
6.
Определение: Дискретной называют случайнуювеличину, которая принимает отдельные, изолированные
возможные значения с определенными вероятностями.
Число возможных значений ДСВ может быть конечным
или бесконечным.
К дискретным случайным величинам относятся:
• число попаданий в мишень при выстреле,
• число яиц на птицефабриках,
• число вызовов на телефонной станции и т. п.
Составитель: Самойлова О.А.
7.
Закон распределения вероятностейдискретной случайной величины
Для задания ДСВ недостаточно перечислить все ее
возможные значения. Ведь в действительности ДСВ
могут иметь одинаковые перечни возможных значений,
а вероятности их разные. Поэтому для ДСВ необходимо
указывать не только все возможные ее значения, но и
указывать вероятности принятия этих значений.
Определение: Законом распределения дискретной
случайной величины называют соответствие между
возможными значениями и их вероятностями.
Составитель: Самойлова О.А.
8.
Закон распределения ДСВ можно задать таблично,аналитически (в виде формулы) и графически.
При табличном задании закона распределения ДСВ
первая строка таблицы содержит возможные значения,
а вторая – их вероятности.
xi
pi
x1
p1
x2
p2
...
...
xn
pn
Так как в одном испытании случайная величина принимает
одно и только одно возможное значение, то события
X x1 , X x2 ,..., X xn образуют полную группу;
следовательно, сумма вероятностей этих событий, т.е.
сумма второй строки таблицы равна единице:
p1 p2 ... pn 1.
Составитель: Самойлова О.А.
9.
Пример: В денежной лотерее выпущено 100 билетов.Разыгрывается один выигрыш в 50 руб. и десять выигрышей
по 1 руб. Найти закон распределения случайной величины
X – стоимости возможного выигрыша для владельца одного
лотерейного билета.
Решение:
x1 50, x2 1, x3 0.
Напишем возможные значения X:
Вероятности этих возможных значений таковы:
1
10
p1
0,01, p2
0,1, p3 1 ( p1 p2 ) 0,89.
100
100
Напишем искомый закон распределения:
xi
pi
50
1
0
Контроль:
0,01
0,1
0,89
0,01 0,1 0,89 1.
Составитель: Самойлова О.А.
10.
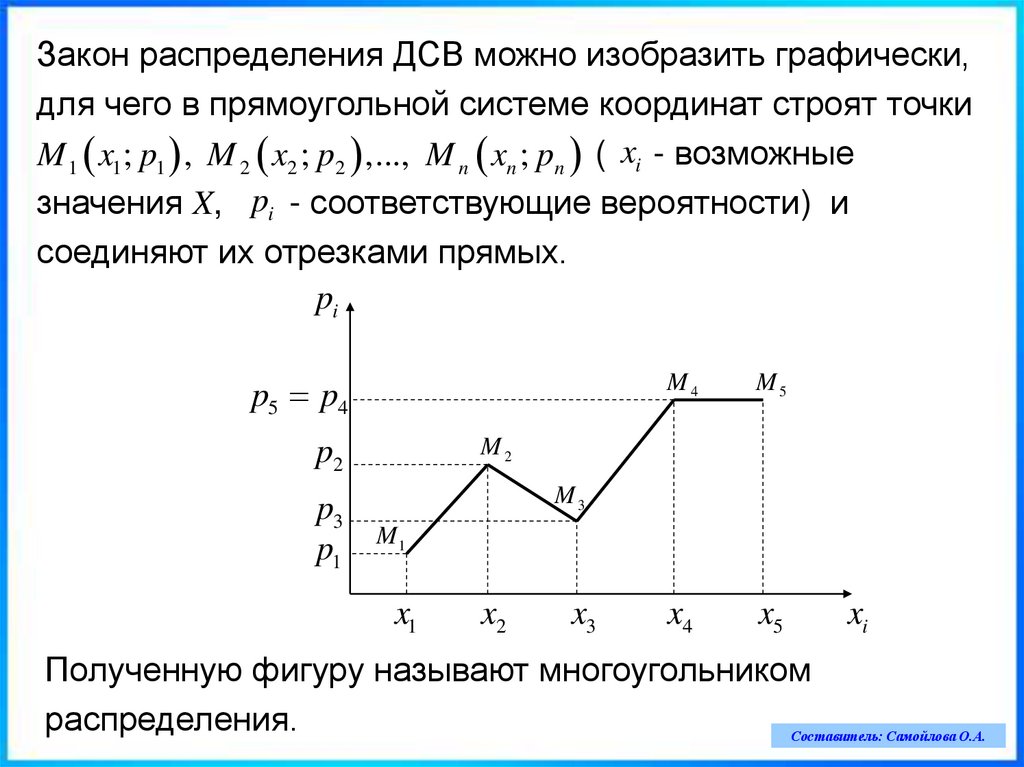
Закон распределения ДСВ можно изобразить графически,для чего в прямоугольной системе координат строят точки
M 1 x1 ; p1 , M 2 x2 ; p2 ,..., M n xn ; pn ( xi - возможные
значения X, pi - соответствующие вероятности) и
соединяют их отрезками прямых.
pi
p5 p4
M5
x4
x5
M2
p2
p3
p1
M4
M3
M1
x1
x2
x3
xi
Полученную фигуру называют многоугольником
распределения.
Составитель: Самойлова О.А.
11.
Пример: Дискретная случайная величина X задана закономраспределения:
xi
pi
1
3
6
8
0,2
0,1
0,4
0,3
Построить многоугольник распределения.
Решение:
Построим прямоугольную систему координат, причем по
оси абсцисс будем откладывать всевозможные значения
pi .
а по оси ординат - соответствующие вероятности
xi ,
Составитель: Самойлова О.А.
12.
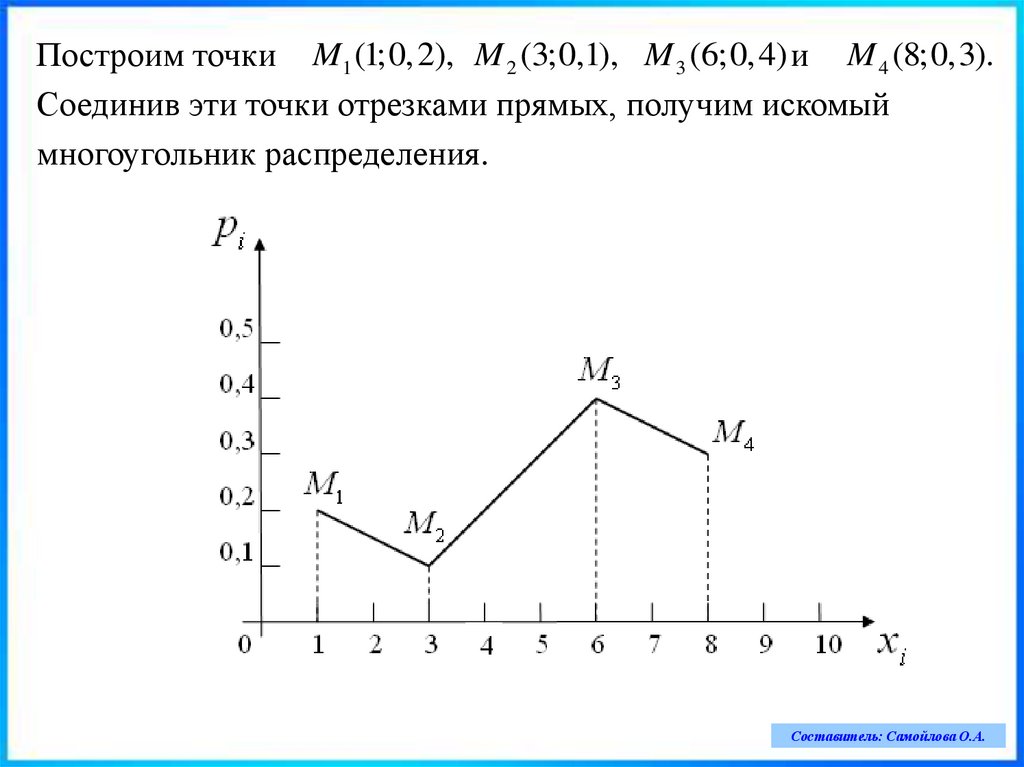
Построим точки M1 (1;0, 2), M 2 (3;0,1), M 3 (6;0, 4) и M 4 (8;0,3).Соединив эти точки отрезками прямых, получим искомый
многоугольник распределения.
Составитель: Самойлова О.А.
13. Биномиальный закон распределения
Пусть производится n независимых испытаний, вкаждом из которых событие A может появиться или не
появиться. Вероятность появления события во всех
испытаниях постоянна и равна p.
Следовательно, вероятность непоявления q 1 p.
Рассмотрим дискретную случайную величину X – число
появлений события A в этих испытаниях.
Требуется найти закон распределения случайной
величины X.
Составитель: Самойлова О.А.
14.
Для нахождения закона распределения рассматриваемойДСВ X требуется определить возможные значения ДСВ X
и их вероятности.
Так как ДСВ X характеризует число появлений события A
в n испытаниях, то она принимает только целочисленные
значения (0 – ни разу не появилось, 1 – один раз
появилось и т. д.).
При заданных условиях вероятность появления события A
k раз в n независимых испытаниях определяется по
формуле Бернулли. Таким образом, формула Бернулли
является аналитическим заданием указанного закона
распределения.
Составитель: Самойлова О.А.
15.
Определение: Дискретная случайная величина X имеетбиномиальный закон распределения с параметрами n и p,
если она принимает значения 0, 1, 2,…, k,…n с
вероятностями
P X k Cnk p k q n k
где 0 p 1, q 1 p.
Напишем биномиальный закон в виде таблицы:
...
xi
0
pi
q n Cn1 p1 q n 1 Cn2 p 2 q n 2 ... Cnk p k q n k
1
2
...n
k
pn
Составитель: Самойлова О.А.
16.
Пример: Устройство состоит из трех независимоработающих элементов. Вероятность отказа каждого
элемента равна 0,1. Составить биномиальное
распределение вероятностей числа отказавших элементов.
Решение:
P3 0 0,9 0,729;
3
P3 1 C13 0,1 0,9 0, 243;
1
2
P3 2 C 0,1 0,9 0,027;
2
3
2
1
P3 3 0,1 0,001.
3
Таким образом биномиальное распределение имеет вид
xi
pi
0
1
2
3
0,729 0,243 0,027 0,001
p 1.
i
Составитель: Самойлова О.А.




















 mathematics
mathematics








