Similar presentations:
Случайные величины
1.
СЛУЧАЙНЫЕВЕЛИЧИНЫ
2.
Тема. Дискретныеслучайные
величины
(ДСВ)
3.
1. Виды случайных величинОдним из важнейших понятий в
теории
вероятностей
является
понятие случайной величины.
Величина называется случайной,
если в результате опыта она может
принимать
любые
заранее
неизвестные значения.
4.
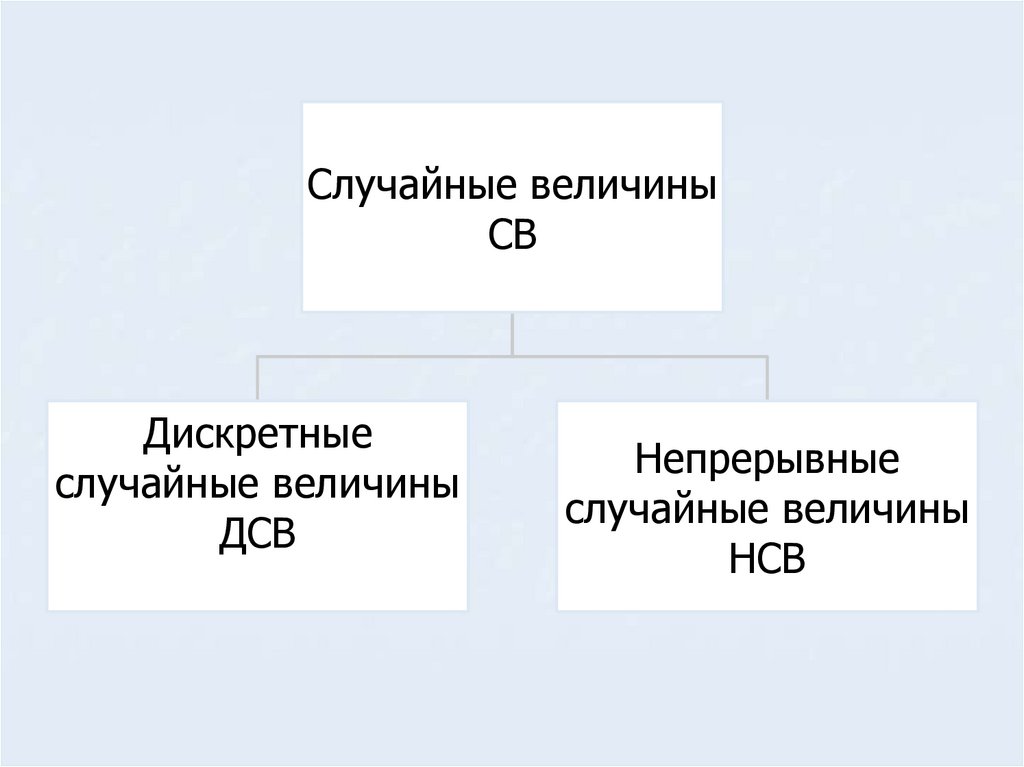
Случайные величиныCВ
Дискретные
случайные величины
ДСВ
Непрерывные
случайные величины
НСВ
5.
Дискретнаяслучайная
величина
(ДСВ)
–
это
случайная величина, которая
принимает
отдельное
изолированное,
счетное
множество значений.
Пример. Число посетителей
поликлиники в течение дня.
6.
Непрерывнаяслучайная
величина
(НСВ)
–
это
случайная
величина,
принимающая любые значения
из некоторого промежутка.
Пример.
Масса
наугад
выбранной таблетки некоторого
препарата.
7.
Случайные величины обозначаютзаглавными буквами латинского
алфавита: X, Y, Z и т.д.,
а их значения – соответствующими
строчными буквами: x, y, z и т. д.
8.
Пример.Если
случайная
величина X имеет три возможных
значения, то они могут быть
обозначены так: x1, x2, x3.
X: x1, x2, x3.
9.
2. Распределение дискретнойслучайной величины
Законом распределения ДСВ
называют
соответствие
между
возможными
значениями
и
их
вероятностями.
Закон
распределения
можно
представить
в
виде
таблицы,
формулы, графически.
10.
При табличном задании законараспределения ДСВ первая строка
таблицы
содержит
возможные
значения, а вторая – их вероятности:
X
x1
x2
…
xn
P
p1
p2
…
pn
11.
Приняв во внимание, что в одномиспытании СВ принимает одно и только
одно возможное значение, получаем, что
события
X=x1 , X=x2 ,…, X=xn образуют полную
группу, следовательно сумма вероятностей
этих событий, то есть сумма вероятностей
второй строки таблицы, равна единице:
p1+p2+…+pn=1.
12.
pp2
p1
pn
0
x1
x2
…
…
xn
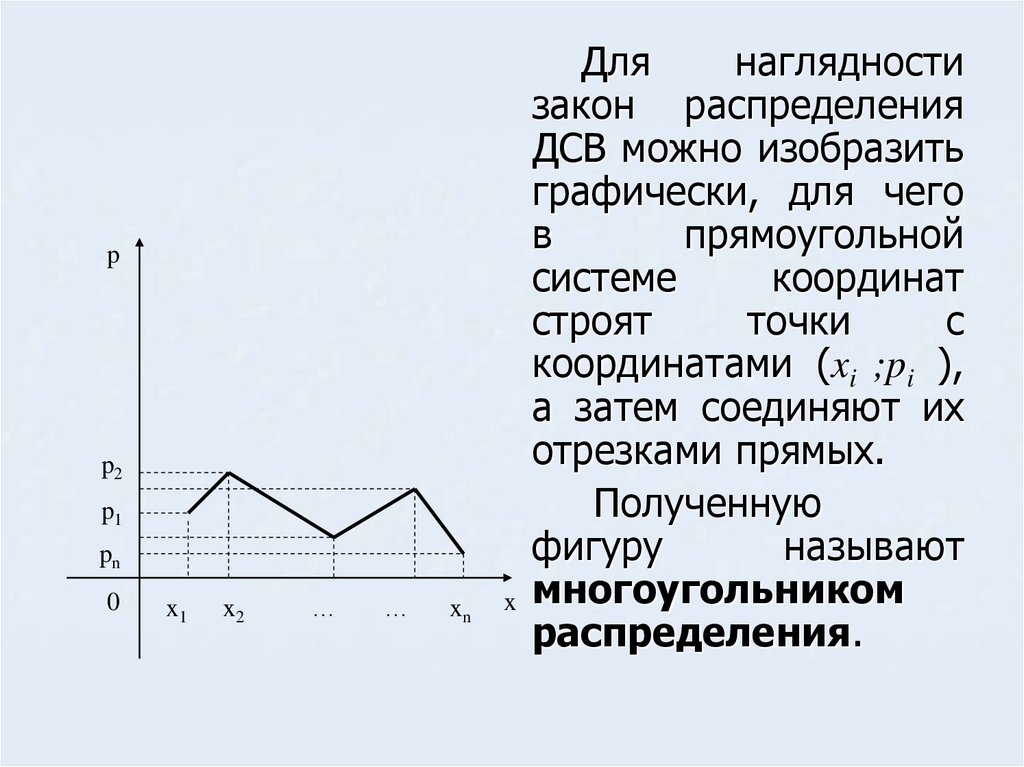
Для
наглядности
закон распределения
ДСВ можно изобразить
графически, для чего
в
прямоугольной
системе
координат
строят
точки
с
координатами (xi ;pi ),
а затем соединяют их
отрезками прямых.
Полученную
фигуру
называют
x многоугольником
распределения.
13.
3. Функция распределенияФункцией распределения случайной
величины X называется функция
действительной
переменной
x,
определяемая равенством F(x)=P(X<x).
Ее также называют интегральной
функцией распределения ДСВ и НСВ.
14.
Так как до значения x1 случайная величина Xне встречалась, то и вероятность события X< x1
равна нулю.
Для всех значений x1<x x2 вероятность
события X<x совпадает с вероятностью значения
x1, т. е. p1.
Но при x>x2 СВ уже может принимать два
возможных значения x1 и x2 , поэтому
вероятность события X<x для x2<x x3 будет
равна сумме вероятностей p1+p2 и т.д.
15.
Если дискретные значения случайнойвеличины x1, x2 , … ,xn расположены в
порядке возрастания, то каждому значению
xi этих величин ставится в соответствие
сумма вероятностей всех предыдущих
значений и вероятности pi:
x1
x2
x3
…
xn
p1 p1+ p2 p1+ p2 + p3 … p1+ p2 + p3+ … + pn
16.
0,p
1
F x p1 p2
...
1
при
при
при
...
при
x x1 ;
x1 x x2 ;
x2 x x3 ;
...
x xn .
17.
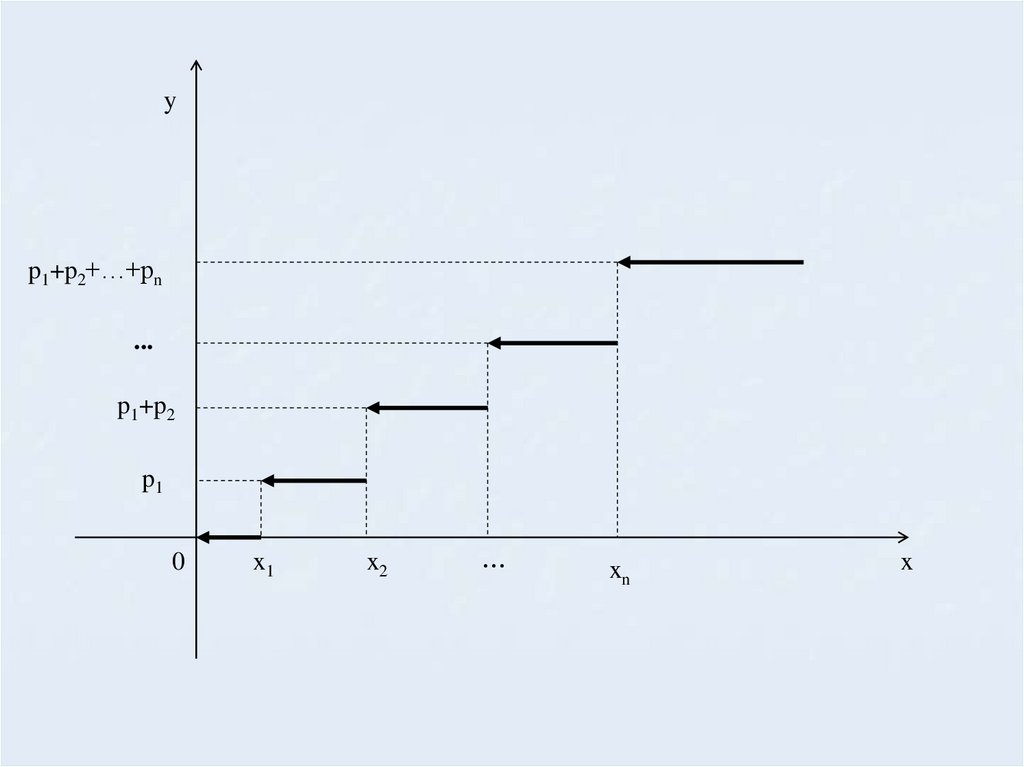
Нанося на график возможныезначения ДСВ X и соответствующие
суммы
вероятностей,
получаем
ступенчатую фигуру, которая и
является
графиком
функции
распределения вероятностей.
18.
yp1+p2+…+pn
...
p1+p2
p1
0
x1
x2
…
xn
x
19.
Свойства функциираспределения случайной
величины X
1)0 F x 1;
2) x1 x2 F x1 F x2
20.
ПримерМонета бросается три раза. Случайная
величина Х – число выпавших гербов.
Построить для нее:
ряд распределения,
многоугольник распределения,
функцию распределения.
21.
Решение.Случайная величина
Х может принять
значения: 0, 1, 2, 3. Соответствующие
этим значениям вероятности находятся
по формуле Бернулли Рm,n= Сnm· pm·qn-m.
22.
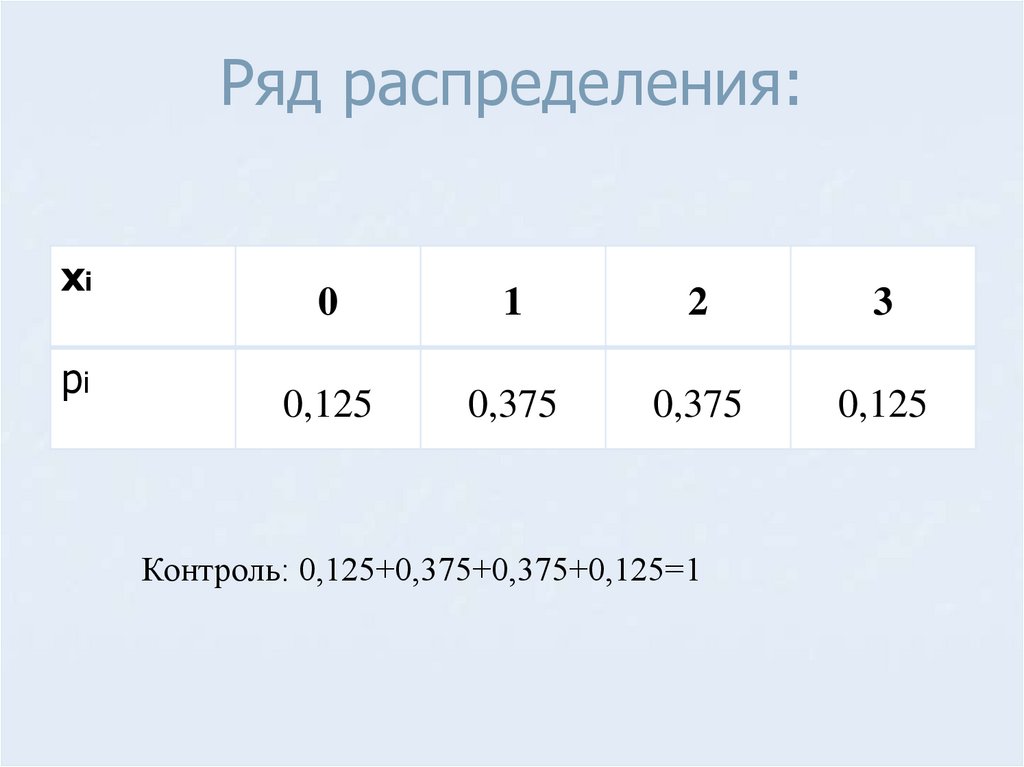
Ряд распределения:xi
pi
0
1
2
3
0,125
0,375
0,375
0,125
Контроль: 0,125+0,375+0,375+0,125=1
23.
Многоугольник распределенияр
0,4
0,35
0,3
0,25
0,2
р
0,15
0,1
0,05
0
0
1
2
3
24.
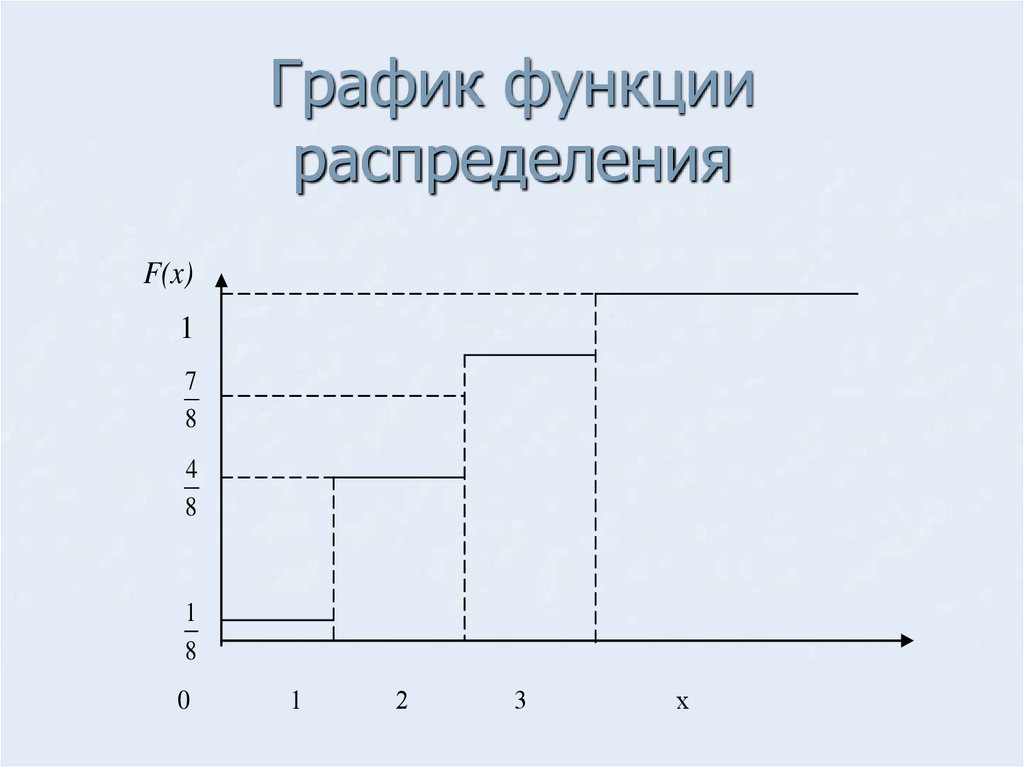
Функция распределения25.
График функциираспределения
F(x)
1
7
8
4
8
1
8
0
1
2
3
х
26.
4. Числовые характеристикидискретных случайных
величин
27.
1). Математическое ожидание иего свойства
Математическим ожиданием ДСВ X называется
сумма произведений всех ее значений на
соответствующие вероятности.
n
M X x1 p1 x2 p2 ... xn pn xi pi
i 1
28.
Вероятностный смыслматематического ожидания:
Математическое ожидание приближенно
равно
среднему
арифметическому
наблюдаемых
значений
случайной
величины. (На числовой оси возможные
значения расположены слева и справа от
математического
ожидания,
т.
е.
математическое
ожидание
больше
наименьшего
и
меньше
наибольшего
возможных значений).
29.
Свойства математическогоожидания
1.
Математическое
ожидание
постоянной
величины равно самой постоянной
M C C
2. Постоянный множитель можно выносить за
знак математического ожидания
M CX C M X
30.
3. Математическое ожидание суммыконечного числа случайных величин равно
сумме их математических ожиданий
M X Y M X M Y
31.
4.Математическое
ожидание
произведения конечного числа независимых
случайных величин равно произведению их
математических ожиданий.
(Две случайные величины называются
независимыми, если закон распределения
одной из них не зависит от того, какие
возможные
значения
приняла
другая
величина)
M X Y M X M Y
32.
2). Дисперсия и ее свойстваДисперсией (рассеянием) ДСВ
называется математическое ожидание
квадрата
отклонения
СВ
от
ее
математического ожидания
D X M X M X
2
33.
Свойства дисперсии:1. Дисперсия постоянной величины равна
нулю
D C 0
34.
2. Постоянный множитель можновыносить
за
знак
дисперсии,
возводя его в квадрат
D CX C D X
2
35.
3. Дисперсия суммы конечного числанезависимых СВ равна сумме их
дисперсий
D X Y D X D Y
36.
Теорема. Дисперсия ДСВ равна разностимежду математическим ожиданием квадрата
ДСВ X и квадратом ее математического
ожидания
D X M X M X
2
2
37.
3). Среднее квадратическоеотклонение
Средним квадратическим отклонением
случайной
величины
X
называется
арифметическое
значение
корня
квадратного из ее дисперсии
X D X
38.
Пример.Вычислить
математическое
ожидание,
дисперсию,
среднее
квадратическое
отклонение дискретной случайной величины X,
определяемой как количество студентов в
наугад
выбранной
группе,
используя
следующие данные:
X
8
9
10
11
12
P
0,2
0,1
0,3
0,2
0,2
39.
M X 8 0,2 9 0,1 10 0,3 11 0,2 12 0,21,6 0,9 3 2,2 2,4 10,1;
40.
D X 8 0,2 9 0,1 10 0,32
2
2
11 0,2 12 0,2 10,1
103,9 102,01 1,89;
2
2
X 1,89 1,37.
2
41.
1. Биномиальный законраспределения.
Дискретная случайная величина Х имеет биномиальный закон распределения, если она
принимает значения 0, 1, 2, …, m, …, n c вероятностями , где 0 < p < 1, q=1-p, m=0, 1, …, n.
Ряд распределения биномиального закона имеет вид:
42.
2. Закон распределенияПуассона.
Дискретная случайная величина Х имеет закон распределения
Пуассона, если она принимает значения 0, 1, 2, …, m, … (бесконечное,
но счетное множество значений) с вероятностями
Ряд распределения закона Пуассона имеет вид:

































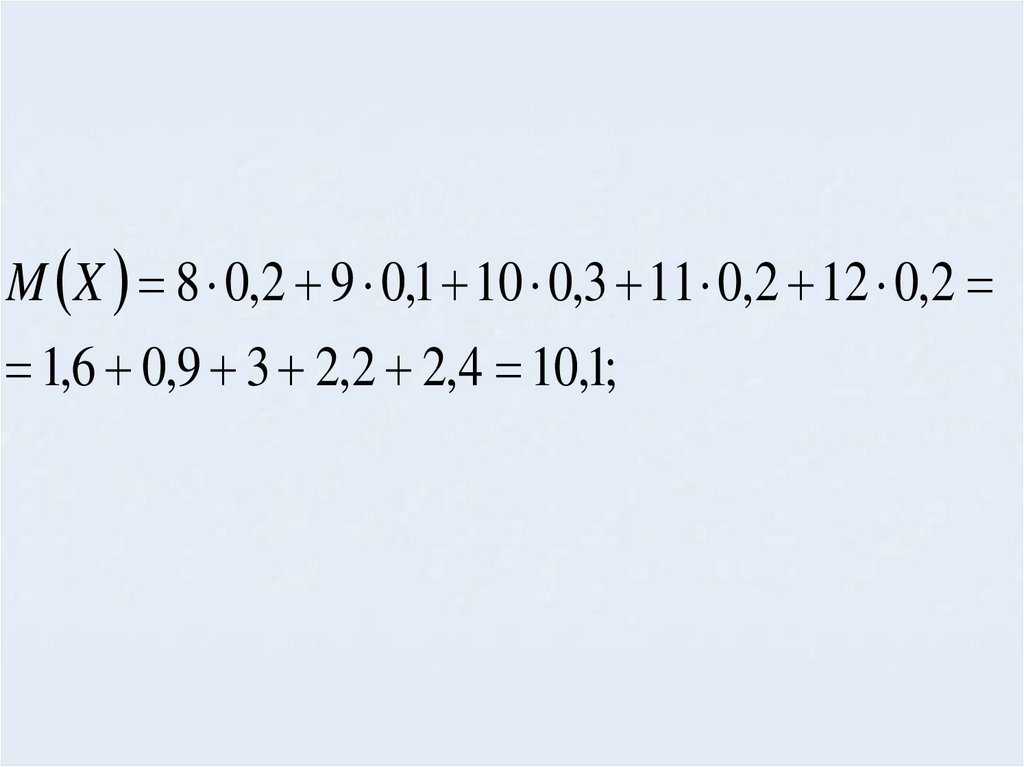
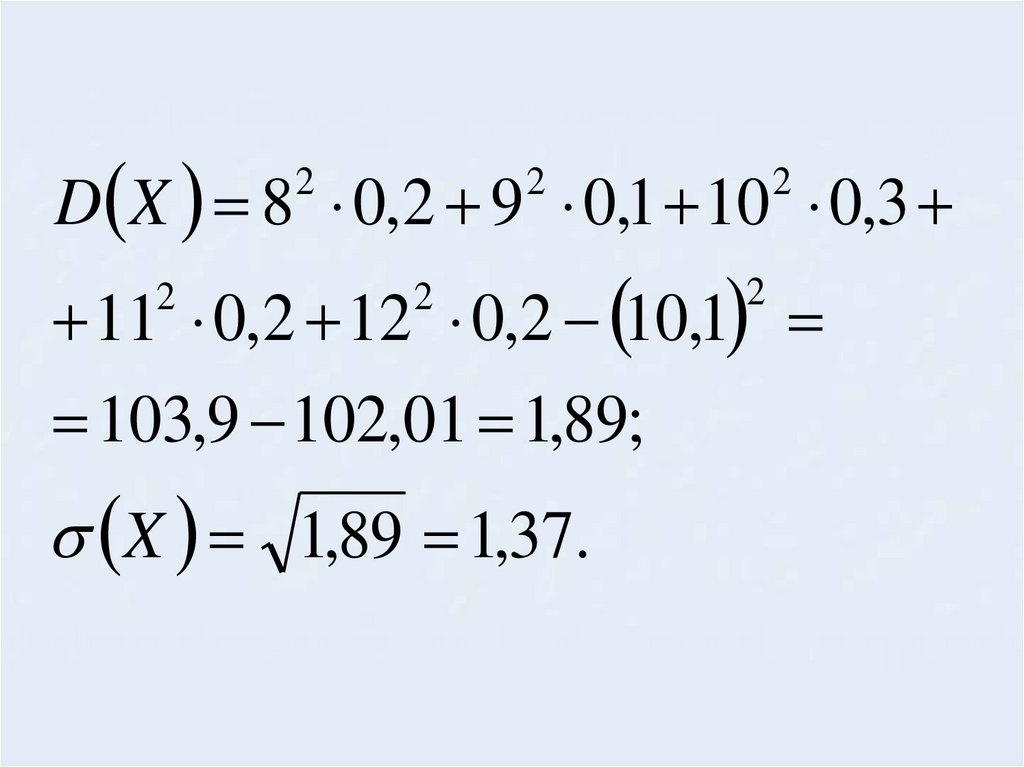




 mathematics
mathematics








