Л7-8 _ТЙКС

1.

1

2.

КИЇВСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ
імені ТАРАСА ШЕВЧЕНКА
Кафедра інформаційних систем та технологій
ТЕОРІЯ ЙМОВІРНОСТЕЙ та КОМП'ЮТЕРНА СТАТИСТИКА
Викладачі: Володимир ДРУЖИНІН; Ганна ТЕРЕЩУК
2024

3.

ЛЕКЦІЯ № 7: «Інтервальна оцінка математичного сподівання. Інтервальна
оцінка середнього квадратичного відхилення. Інтервальна оцінка коефіцієнта
кореляції. Статистична перевірка статистичних гіпотез. Основні поняття»
Навчальні питання:
1. Інтервальна оцінка математичного очікування.
2. Інтервальна оцінка середнього квадратичного відхилення.
3. Інтервальна оцінка коефіцієнта кореляції.
4. Статистична перевірка гіпотез. Основні поняття.
2

4.

1. Інтервальна оцінка математичного очікування
Точковою оцінкою математичного очікування є вибіркове середнє.
!!! При визначенні інтервальних оцінок розглянемо окремо два
випадки.
3

5.

4

6.

*** Якщо позначити
тобто t дорівнює значенню аргументу, для якого функція Лапласа
приймає значення, яке дорівнює
Знаючи t, знаходимо величину ε, і інтервальна оцінка математичного
очікування при відомій дисперсії вимірювань приймає вид
5

7.

!!! Аналіз формули свідчить, що інтервал тим більший, чим більша
похибка вимірювань (вона задається величиною σ) і чим менше виконано
вимірювань n.
Слід також нагадати, що складена нерівність слушна з ймовірністю γ і
чим більша надійність, тим більший інтервал 2ε, бо функція Ф(х) є
монотонно зростаючою (хоч і нелінійно).
5

8.

2. Дисперсія результатів вимірювань невідома
6

9.

де σ – невідоме істинне значення середнього квадратичного відхилення.
Ділене є стандартизованою величиною (тобто величина розподілена за
нормальним законом з параметрами (0, 1)).
Дільник під коренем містить випадкову величину з розподілом
(«хі-квадрат» розподіл з (n–1) ступенем свободи).
*** Як відомо, відношення цих розподілів є розподілом Стьюдента з (n–1) ступенем
свободи.
Враховуючи, що розподіл Стьюдента є симетричним, будемо шукати такі значення
t, щоб виконувалась нерівність
7

10.

!!! За означенням, ймовірність цієї нерівності дорівнює значенню
функції розподілу для аргументу t.
Отже, значення t можна знайти або за таблицями критичних точок
розподілу Стьюдента для фіксованих значень γ в залежності від об’єму
вибірки n (таблиці додатку), або як аргумент функції розподілу
Стьюдента.
Крім того, для знаходження параметра t можна використати
стандартну функцію табличного процесора
MS Excel СТЬЮДРАСПОБР(α, n–1).
Остаточно інтервальну оцінку шукають за формулою
8

11.

!!! Зрозуміло, що для однакових за об’ємом вибірок і однакових рівнів
значущості α інтервальні оцінки математичного очікування при
невідомій дисперсії більші, ніж при відомій, що є наслідком відсутності
інформації про похибки вимірювань.
9

12.

2. Інтервальна оцінка середнього квадратичного відхилення
*** Нехай за вибіркою об’ємом n обчислене вибіркове значення
стандартного відхилення S і з заданою наперед надійністю γ слід
відшукати інтервал, на якому знаходиться невідоме значення σ – середнє
квадратичне (стандартне ) відхилення генеральної сукупності.
Поділимо вираз для обчислення незміщеної оцінки дисперсії
на дисперсію
та отримаємо
10

13.

Сума квадратів нормалізованих випадкових величин в правій частині
має розподіл
з (n–1) ступенем свободи), отже, величина
розподілена за таким же законом.
При невеликих об’ємах вибірки хі-квадратрозподіл суттєво
відрізняється від симетричного, тому границі інтервалу надійності
несиметричні відносно центру.
Будемо шукати такий інтервал (z1, z2), щоб виконувались нерівності
11

14.

Будемо шукати такий інтервал (z1, z2), щоб виконувались нерівності
!!! Використаємо властивість інтегральної функції розподілу.
12

15.

звідки одержуємо оцінку середнього
генеральної сукупності у вигляді
квадратичного
відхилу
13

16.

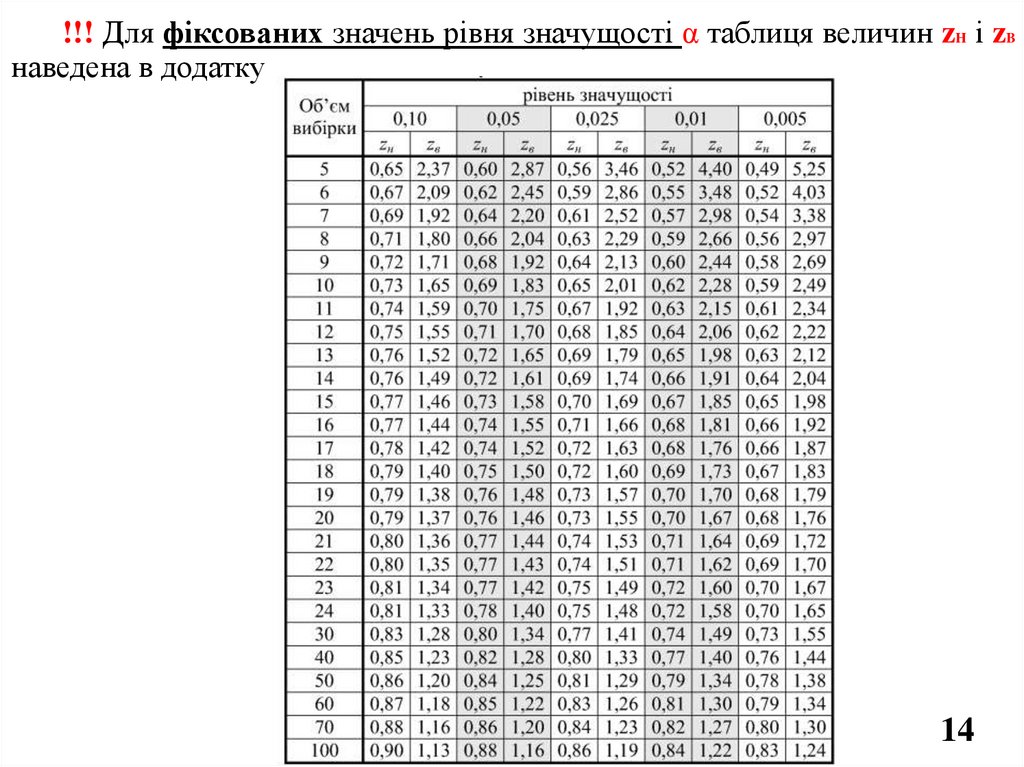
!!! Для фіксованих значень рівня значущості α таблиця величин zH і zB
наведена в додатку
14

17.

!!! Для довільних значень α можна скористатись таблицею інтеграла
ймовірностей хі-квадрат розподілу.
!!! В середовищі Excel можна скористатися статистичною функцією
ХИ2ОБР(х, n –1);
враховуючи, що
Fп-1(х)=1–ХИ2РАСП(х, п–1)
слід обчислювати
F =ХИ2РАСП(α/2).
15

18.

3. Інтервальна оцінка коефіцієнта кореляції
*** Вам вже відомо, що вибіркове значення коефіцієнта кореляції
шукається за формулою
Розглянемо задачу пошуку інтервальної оцінки для істинного значення
коефіцієнту кореляції, яке позначимо
ρ=М(r).
16

19.

Закон розподілу випадкової величини r при
ρ≠0
є несиметричним і при збільшенні об’єму вибірки n він дуже
повільно збігається до нормального з параметрами
M(r) = ρ
!!! Тому для обмежених вибірок доцільно ввести допоміжну величину
з відомим законом розподілу, для неї знайти інтервальну оцінку і
повернутись до вихідної величини – вибіркового коефіцієнту кореляції.
*** Зазвичай користуються так званим z - перетворенням Фішера
17

20.

тобто Z дорівнює оберненому гіперболічному тангенсу величини r.
!!! Розподіл Z навіть для малих вибірок швидко збігається до
нормального з числовими характеристиками
Інтервальна оцінка
відповідності з формулою
нормально
розподіленої
величини
Z
дається співвідношенням
18
у

21.

!!! Значення r1 , r2 і визначають інтервальну оцінку коефіцієнта
кореляції.
*** Прямі і зворотні перетворення Фішера виконуються або за
наведеними вище формулами, або за відповідними таблицями, або з
використанням статистичних функцій
Excel ФИШЕР(х) і ФИШЕРОБР(у)
19

22.

4. Статистична перевірка статистичних гіпотез. Основні поняття
Математична статистика розв’язує дві основні задачі:
знаходження статистичних оцінок вибіркових сукупностей (точкових
і інтервальних)
і
перевірка деяких припущень (гіпотез) відносно параметрів розподілу
вибірки.
!!! Висунення (формулювання) і перевірка (підтвердження чи
спростування) гіпотез є обов’язковим етапом прийняття рішення на
основі опрацювання статистичних даних.
20

23.

!!! В теорії ймовірностей гіпотези інтерпретуються як несумісні події,
що утворюють повну групу.
*** Формалізувати задачу перевірки гіпотез легше, якщо їх кількість
обмежити двома протилежними подіями.
Позначимо
21

24.

!!! В процесі прийняття рішення і наступної перевірки
справедливості гіпотези можливі чотири ситуації (прийняття рішення
відносно слушності гіпотези і перевірка правильності цього рішення можуть
бути віддалені в часі чи просторі на досить велику відстань).
1. Основну гіпотезу прийнято і вона виявилася слушною.
2. Основну гіпотезу відхилено, і дійсно вона виявилась хибною.
!!! 1, 2 випадки похибок не містять
22

25.

3. Основну гіпотезу відхилено, хоч насправді вона виявилась
слушною.
!!! Така ситуація називається похибкою першого роду.
4. Основну гіпотезу прийнято, а насправді вона виявилась
помилковою
!!! Така ситуація називається похибкою другого роду.
23

26.

Лекцію завершено, дякую за увагу!