Similar presentations:
Кривые и поверхности 2 порядка
1. Кривые и поверхности второго порядка Методические материалы для проведения семинарских занятий с использованием интерактивной
Московский государственный техническийуниверситет им. Н.Э. Баумана
Кафедра «Прикладная математика»
Кривые и поверхности
второго порядка
Методические материалы для проведения семинарских
занятий с использованием интерактивной электронной
доски
О.А. Иванова
Е.Е. Красновский
О.В. Новожилова
2. Содержание
Основные теоретические сведенияЭллипс
Гипербола
Парабола
Поверхности второго порядка
Решение типовых примеров 1 семестра (только
параллельный перенос)
Кривые второго порядка
Поверхности второго порядка
Решение типовых примеров 2 семестра (ортогональные
преобразования и параллельный перенос)
Кривые второго порядка
Поверхности второго порядка
3. Содержание
Вариант 2Содержание
Предисловие
Основные теоретические сведения
Эллипс
Гипербола
Парабола
Поверхности второго порядка
Метод сечений
Решение типовых примеров 1 семестра (только
параллельный перенос)
Кривые второго порядка
Поверхности второго порядка
Решение типовых примеров 2 семестра (ортогональные
преобразования и параллельный перенос)
Кривые второго порядка
Поверхности второго порядка
4.
ПредисловиеКак показывает опыт, при проведении семинарских занятий по
изучению кривых и поверхностей второго порядка с использованием
традиционных доски и мела преподаватель вынужден тратить много времени на
написание формул и, особенно, на создание рисунков. Поэтому сокращается
время на объяснение теоретических основ и, самое главное, на разбор типовых
задач. В результате студенты испытывают трудности при выполнении
домашнего задания и подготовке к контрольным мероприятиям.
Сократить время, затрачиваемое преподавателем на подготовку
графического представления учебного материала, а также существенно
повысить его наглядность можно путём использования интерактивной
электронной доски SMARTBOARD. Таким образом, увеличивается как время,
которое можно потратить на объяснение, так и число рассматриваемых во время
занятия примеров.
Настоящее учебное пособие отражает опыт авторов при проведении
занятий в интерактивной форме по дисциплинам «Аналитическая геометрия» и
«Линейная алгебра» со студентами 1 курса МГТУ им. Н.Э. Баумана с
применением указанной электронной доски.
Содержание пособия отвечает требованиям утвержденных учебных
программ, составленных в рамках перехода к блочно-модульному построению
учебных курсов и балльно-рейтинговой системе оценки знаний, по следующим
дисциплинам: «Аналитическая геометрия» (для факультетов ФН и СМ ),
5.
Предисловие«Линейная алгебра» (для факультета ФН), «Линейная алгебра и функции
нескольких переменных» (для факультета СМ).
Пособие содержит как теоретический материал по кривым и
поверхностям второго порядка, так и 20 примеров решения типовых задач. В
большинстве рассмотренных примеров необходимо привести уравнение кривой
или поверхности второго порядка к каноническому виду либо с помощью
только параллельного переноса (модуль № 2 дисциплины «Аналитическая
геометрия»), либо с помощью комбинации ортогонального преобразования и
параллельного переноса (модуль № 2 дисциплины «Линейная алгебра» и
модуль № 1 дисциплины «Линейная алгебра и функции нескольких
переменных»). Оставшиеся примеры посвящены нахождению уравнения
кривой по приведенным данным, поскольку такие задачи входят в домашнее
задание, предусмотренное модулем № 2 дисциплины «Аналитическая
геометрия».
Настоящее электронное учебное пособие можно использовать при
проведении занятий в интерактивной форме, при самостоятельной работе
студентов, а также при дистанционном обучении, например, с помощью
системы MOODLE.
Пособие предназначено для студентов 1 курса факультетов СМ и ФН
МГТУ им. Н.Э. Баумана.
6.
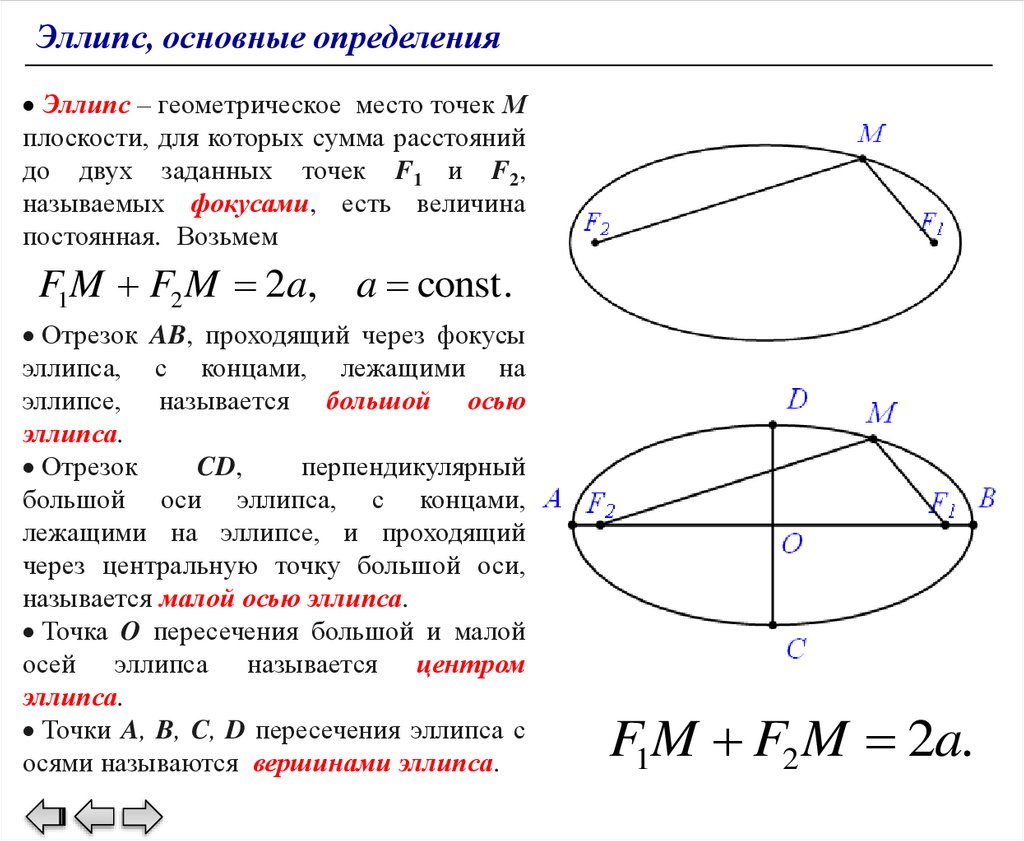
Эллипс, основные определенияЭллипс – геометрическое место точек М
плоскости, для которых сумма расстояний
до двух заданных точек F1 и F2,
называемых фокусами, есть величина
постоянная. Возьмем
F1M F2 M 2a, a const .
Отрезок AB, проходящий через фокусы
эллипса, с концами, лежащими на
эллипсе, называется большой осью
эллипса.
Отрезок
CD,
перпендикулярный
большой оси эллипса, с концами,
лежащими на эллипсе, и проходящий
через центральную точку большой оси,
называется малой осью эллипса.
Точка O пересечения большой и малой
осей эллипса называется центром
эллипса.
Точки A, B, C, D пересечения эллипса с
осями называются вершинами эллипса.
F1M F2 M 2a.
7.
Эллипс, основные определенияОтрезки, проведённые из центра эллипса к вершинам на большой и малой
осях, называются соответственно большой полуосью эллипса и малой
полуосью эллипса и обозначаются a и b.
Отрезки F1M и F2M, соединяющие произвольную точку М на эллипсе с его
фокусами, называются фокальными радиусами.
Расстояние между фокусами называется фокальным расстоянием и
обозначается 2с.
F1M F2 M 2a,
F1F2 2c,
b a 2 c 2 , a c,
c a 2 b 2 , a b.
8.
Каноническое уравнение эллипса с фокусами на оси OxВыберем прямоугольную систему координат Oxy на плоскости так, чтобы ее
начало совпало с центром эллипса, а фокусы находились на оси абсцисс. Такую
систему координат называют канонической для рассматриваемого эллипса, а
соответствующие переменные – каноническими.
Координаты фокусов в канонической системе координат F1 (c,0) и F2 (–c,0).
Каноническое уравнение эллипса
x2 y 2
2 1,
2
a
b
c a2 b2 , a b.
9.
Эксцентриситет и директрисы эллипса с фокусами на оси OxЭксцентриситетом эллипса ε называется отношение расстояния между его
фокусами к длине его большой оси. Чем больше эксцентриситет, тем больше
вытянут эллипс.
Директрисы – это две прямые d1 и d2, перпендикулярные к большой оси
эллипса. Отношение расстояний от любой точки эллипса до фокуса и до
соответствующей директрисы постоянно и равно ε.
2
2
c
a b
a
a
2
b
1 2 1, a b,
a
MF1
,
MN
a
a
d1 : x , d 2 : x .
10.
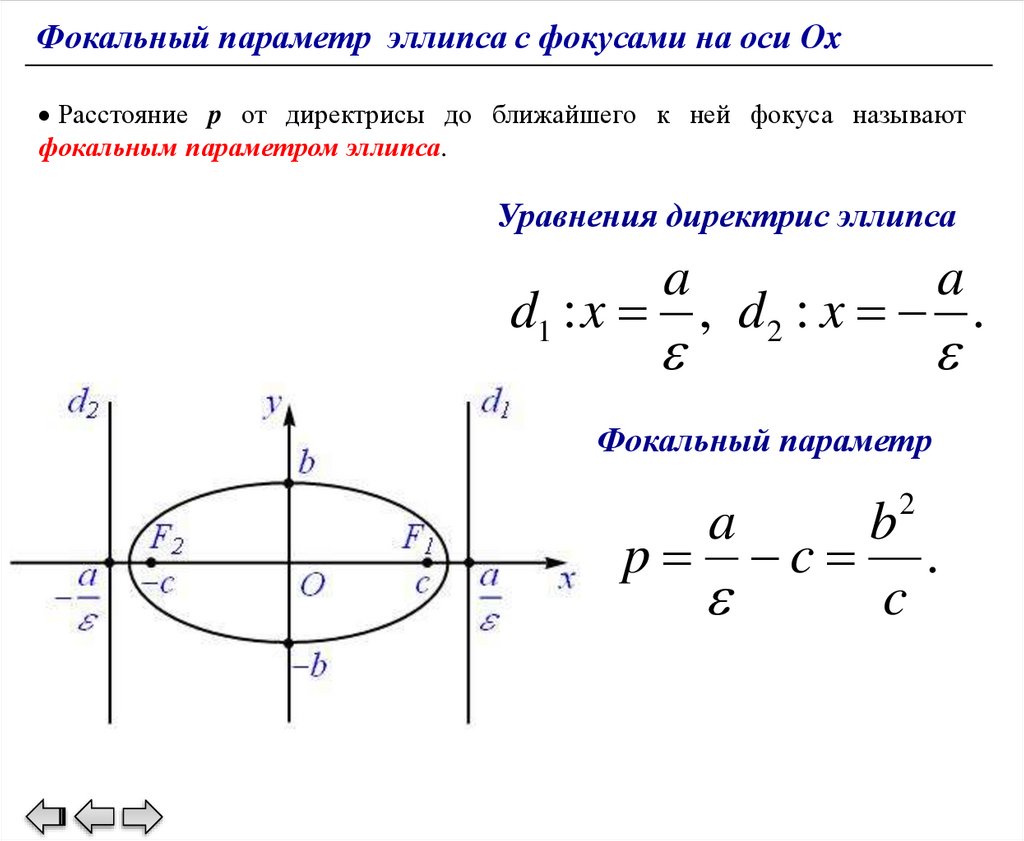
Фокальный параметр эллипса с фокусами на оси OxРасстояние p от директрисы до ближайшего к ней фокуса называют
фокальным параметром эллипса.
Уравнения директрис эллипса
a
a
d1 : x , d 2 : x .
Фокальный параметр
b2
p c .
c
a
11.
Каноническое уравнение эллипса с фокусами на оси OyЕсли b>a, то фокусы эллипса расположены на оси ординат и имеют координаты
F1(0,c) и F2(0,–c).
2
2
x
y
2 1,
2
a
b
c b2 a 2 , b a,
2
c
a
1 2 1.
b
b
Уравнения директрис эллипса
b
b
d1 : y , d 2 : y .
12.
Окружность как эллипс с совпадающими фокусамиЕсли b=a, тогда
x2 y 2
2 1,
2
a
a
x2 y 2 a2
– уравнение окружности с центром
в начале координат, радиуса а.
c a 2 b2 0.
Фокусы F1 и F2 имеют координаты
F1 0,0 , F2 0,0 ,
то есть F1 и F2 располагаются в начале координат и совпадают друг с другом.
13.
Форма эллипса при различных соотношениях полуосейФокусы расположены на оси Ox, a>b.
2
2
x
y
2 1.
2
a
b
1. a=2, b=1, 3 2 0.87 ;
2. a=4, b=1, 15 4 0.97;
3. a=6, b=1, 35 6 0.99;
4. a=6, b=3, 3 2 0.87 .
14.
Форма эллипса при различных соотношениях полуосейФокусы расположены на оси Oy, a<b.
1. a=1, b=2, 3 2 0.87;
2. a=1, b=3, 3 2 0.94;
3. a=3, b=3, 0 ;
4. a=3, b=6, 3 2 0.87.
x2 y 2
2 1.
2
a
b
15.
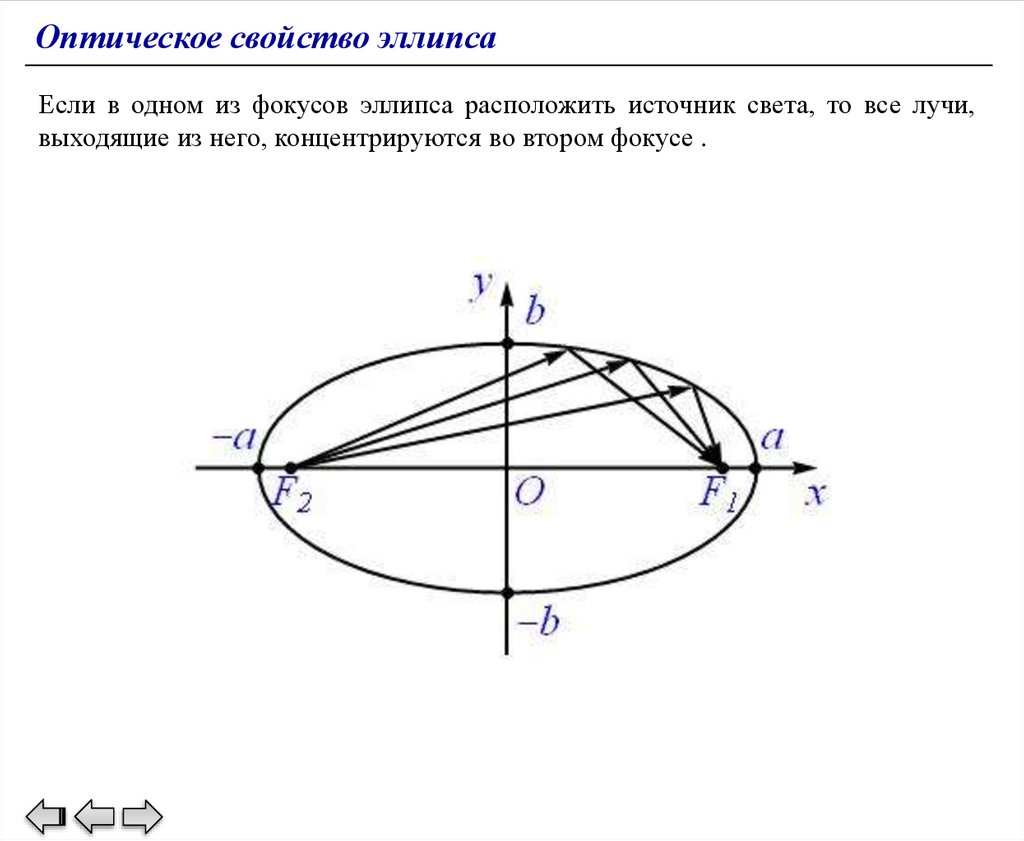
Оптическое свойство эллипсаЕсли в одном из фокусов эллипса расположить источник света, то все лучи,
выходящие из него, концентрируются во втором фокусе .
16.
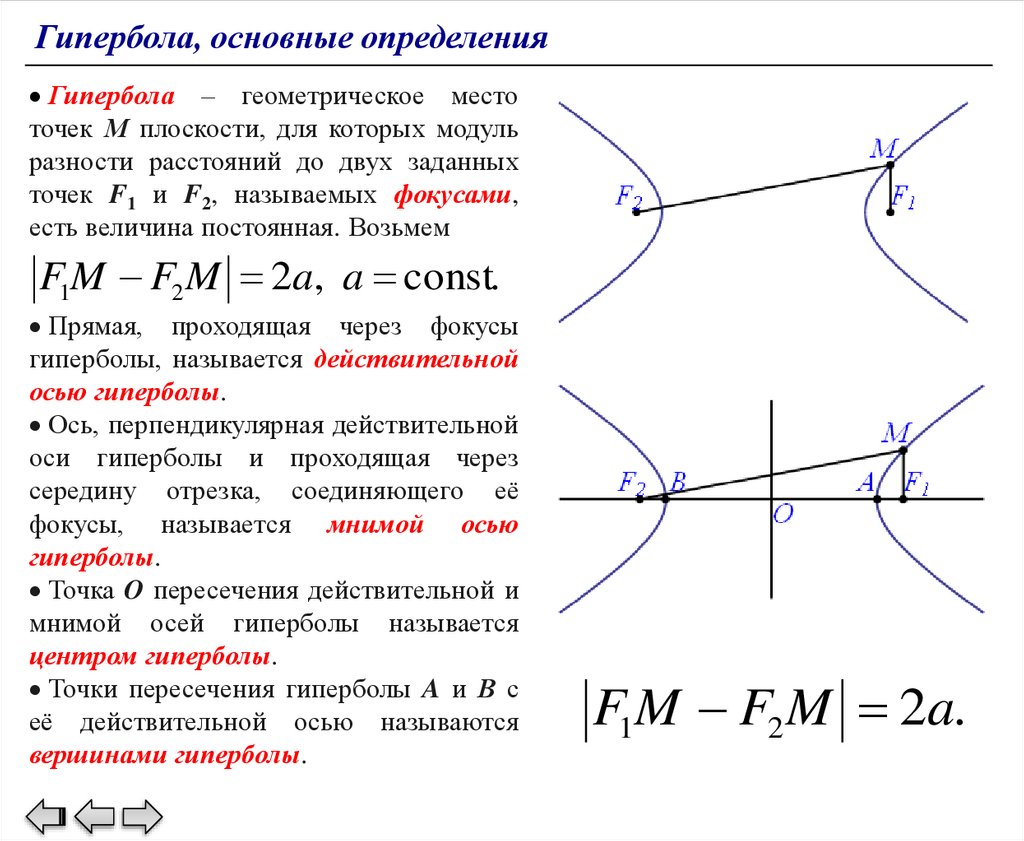
Гипербола, основные определенияГипербола – геометрическое место
точек М плоскости, для которых модуль
разности расстояний до двух заданных
точек F1 и F2, называемых фокусами,
есть величина постоянная. Возьмем
F1M F2 M 2a, a const.
Прямая, проходящая через фокусы
гиперболы, называется действительной
осью гиперболы.
Ось, перпендикулярная действительной
оси гиперболы и проходящая через
середину отрезка, соединяющего её
фокусы, называется мнимой осью
гиперболы.
Точка O пересечения действительной и
мнимой осей гиперболы называется
центром гиперболы.
Точки пересечения гиперболы A и В с
её действительной осью называются
вершинами гиперболы.
F1M F2 M 2a.
17.
Гипербола, основные определенияОтрезок, проведённый из центра гиперболы к её вершинам, называется
действительной полуосью гиперболы и обозначается a.
Отрезки F1M и F2M, соединяющие произвольную точку М на гиперболе с ее
фокусами, называются фокальными радиусами.
Расстояние между фокусами называется фокальным расстоянием и
обозначается 2с.
F1F2 2c,
F1M F2 M 2a.
18.
Каноническое уравнение гиперболы с фокусами на оси OxВыберем прямоугольную систему координат Oxy на плоскости так, чтобы
центр гиперболы находился в начале координат, а фокусы располагались на оси
абсцисс. Такую систему координат называют канонической для
рассматриваемой гиперболы, а соответствующие переменные – каноническими.
Координаты фокусов в канонической системе координат F1 (c,0) и F2 (–c,0).
Каноническое уравнение
гиперболы
2
2
x
y
2 1,
2
a b
• Величину b>0 называют мнимой полуосью
гиперболы.
b c2 a2 ,
c a b .
2
2
19.
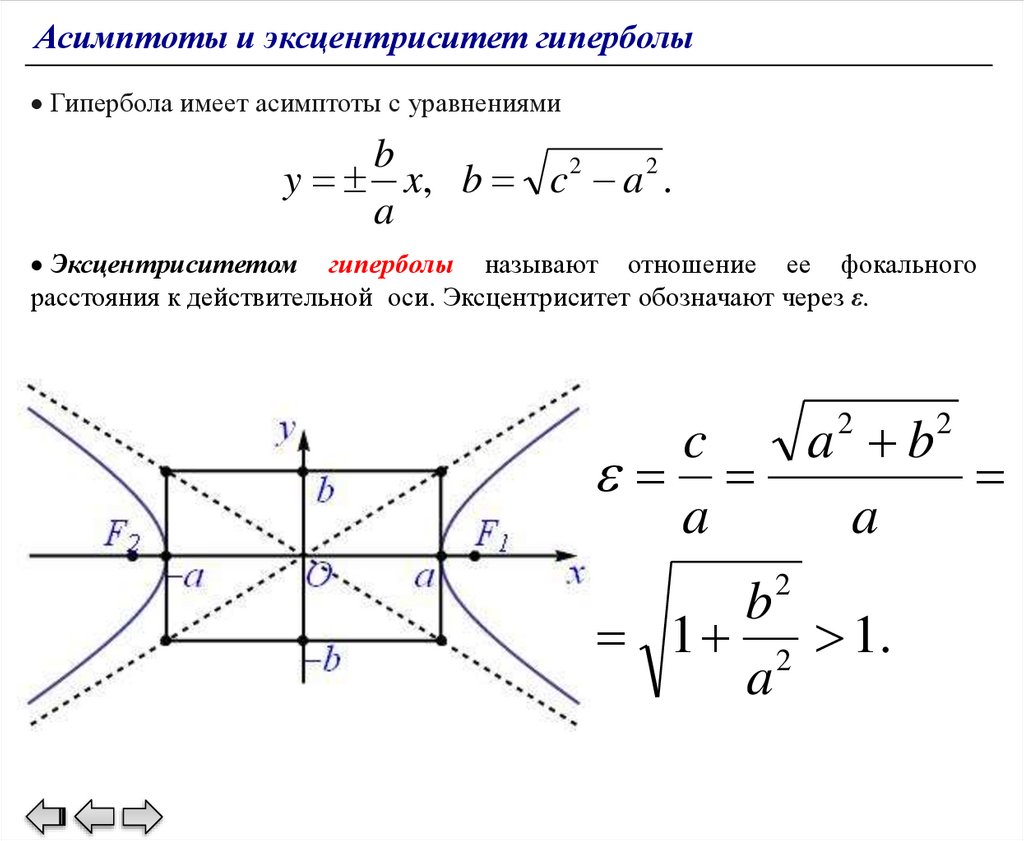
Асимптоты и эксцентриситет гиперболыГипербола имеет асимптоты с уравнениями
b
y x, b c 2 a 2 .
a
Эксцентриситетом гиперболы называют отношение ее фокального
расстояния к действительной оси. Эксцентриситет обозначают через ε.
c
a 2 b2
a
a
2
b
1 2 1.
a
20.
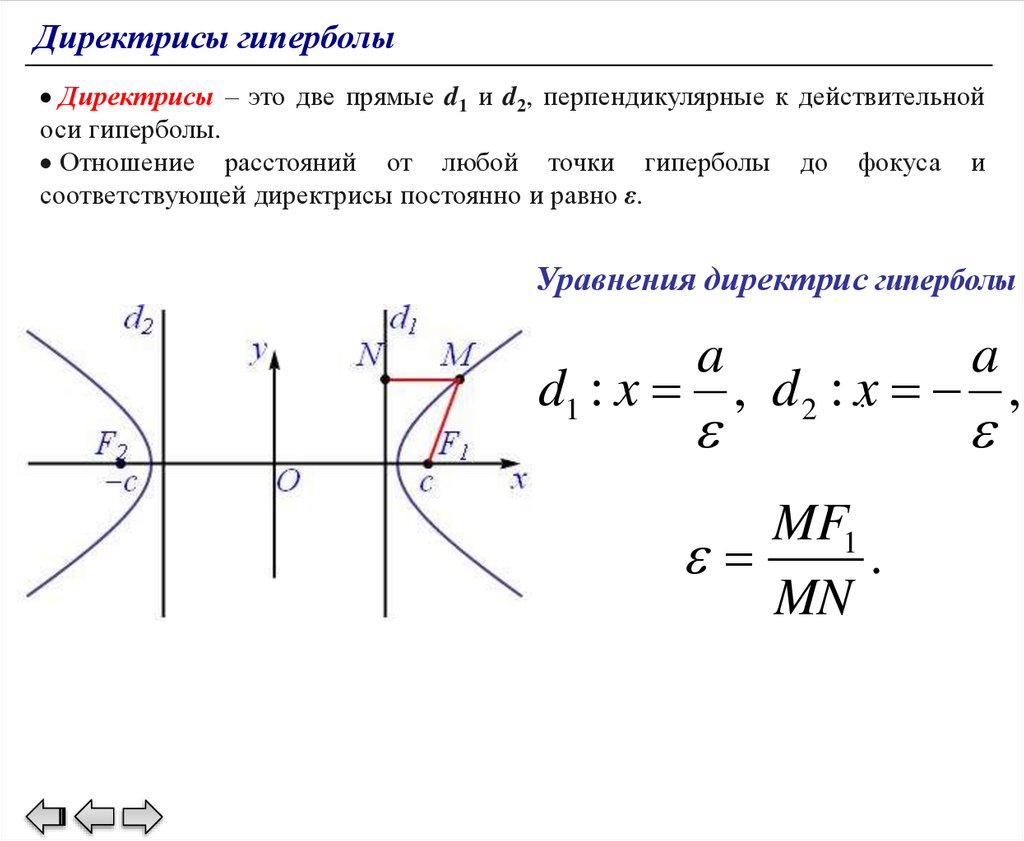
Директрисы гиперболыДиректрисы – это две прямые d1 и d2, перпендикулярные к действительной
оси гиперболы.
Отношение расстояний от любой точки гиперболы до фокуса и
соответствующей директрисы постоянно и равно ε.
Уравнения директрис гиперболы
a
a
d1 : x , d 2 : x. ,
MF1
.
MN
21.
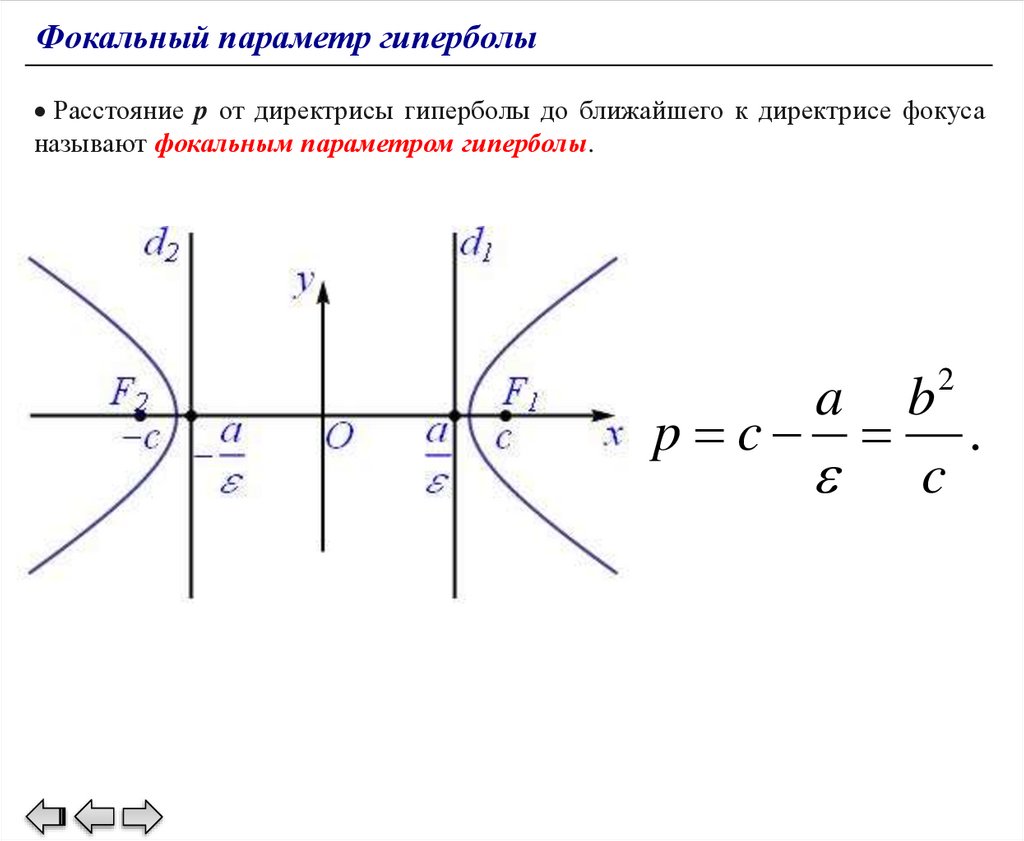
Фокальный параметр гиперболыРасстояние p от директрисы гиперболы до ближайшего к директрисе фокуса
называют фокальным параметром гиперболы.
b2
p c .
c
a
22.
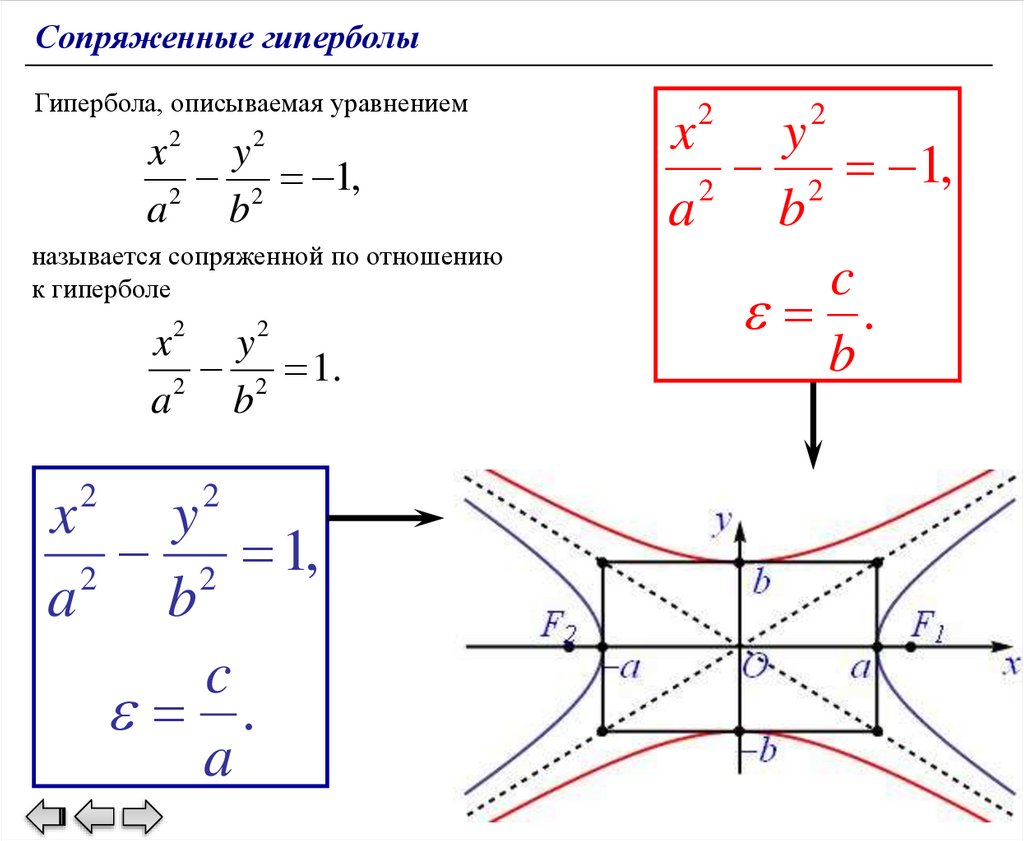
Сопряженные гиперболыГипербола, описываемая уравнением
2
2
x
y
1,
2
2
a b
называется сопряженной по отношению
к гиперболе
x2 y 2
2 1.
2
a
b
x2 y 2
2 1,
2
a
b
c
.
a
x2 y 2
2 1,
2
a
b
c
.
b
23.
Форма гиперболы при различных соотношениях полуосейФокусы расположены на оси Ox.
2
2
x
y
2 1.
2
a b
1. a=2, b=1,
5 2 1.12 ;
2. a=4, b=1,
17 4 1.03;
3. a=6, b=1,
37 6 1.01;
4. a=6, b=3,
5 2 1.12.
24.
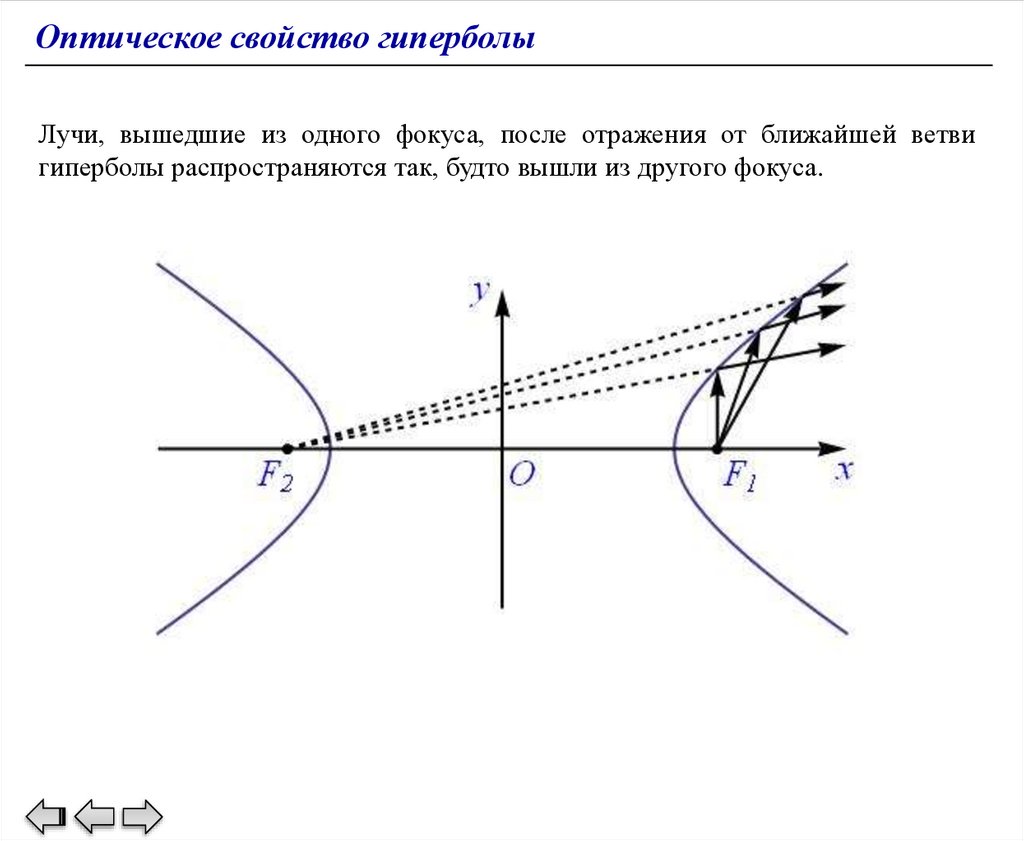
Оптическое свойство гиперболыЛучи, вышедшие из одного фокуса, после отражения от ближайшей ветви
гиперболы распространяются так, будто вышли из другого фокуса.
25.
Гипербола, приведенная к асимптотамЕсли у гиперболы совпадают
действительная
и
мнимая
полуоси, то есть a=b, такую
гиперболу называют
равнобочной или равноосной.
В системе координат O~
x~
yOXY
уравнение равнобочной
гиперболы имеет вид
~
x2 ~
y 2 a2 ,
а в системе координат Oxy
уравнение той же гиперболы
записывается в виде
a2
xy .
2
Данное уравнение называется уравнением гиперболы в асимптотах.
26.
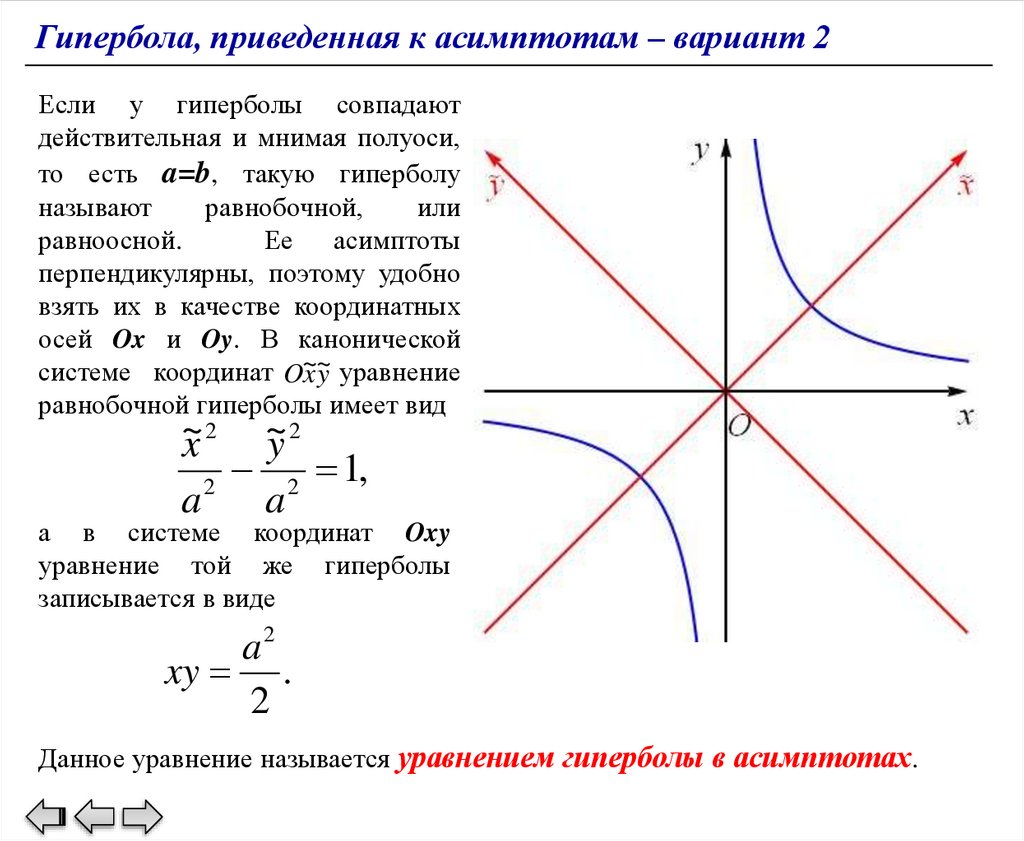
Гипербола, приведенная к асимптотам – вариант 2Если у гиперболы совпадают
действительная и мнимая полуоси,
то есть a=b, такую гиперболу
называют
равнобочной,
или
равноосной.
Ее асимптоты
перпендикулярны, поэтому удобно
взять их в качестве координатных
осей Ox и Oy. В канонической
системе координат O~
x~
y уравнение
равнобочной гиперболы имеет вид
~
x2 ~
y2
2 1,
2
a
a
а в системе координат Oxy
уравнение той же гиперболы
записывается в виде
a2
xy .
2
Данное уравнение называется уравнением гиперболы в асимптотах.
27.
Гипербола, приведенная к асимптотамx~
y
В системе координат O~
вершины гиперболы имеют
координаты А(a,0) и В(-а,0), а
фокусы F1(с,0) и F2(-с,0), где
c a 2.
Следовательно,
в
системе
координат Oxy координаты
вершин гиперболы
2
2
,
A a
,a
2
2
2
2
,
B a
, a
2
2
а фокусов
2
2
2
2
, F2 c
.
F1 c
,c
, c
2
2
2
2
28.
Парабола, основные определенияПарабола – геометрическое
место точек, равноудаленных от
фиксированной точки и от
фиксированной прямой.
Фиксированную
точку
F
называют фокусом параболы, а
прямую
d
–
директрисой
параболы.
Парабола симметрична относительно прямой, перпендикулярной директрисе и проходящей
через фокус параболы. Эту
прямую
называют
осью
параболы.
Парабола пересекает свою ось в
единственной точке O, которую
называют вершиной параболы.
MF MN ,
AO OF.
29.
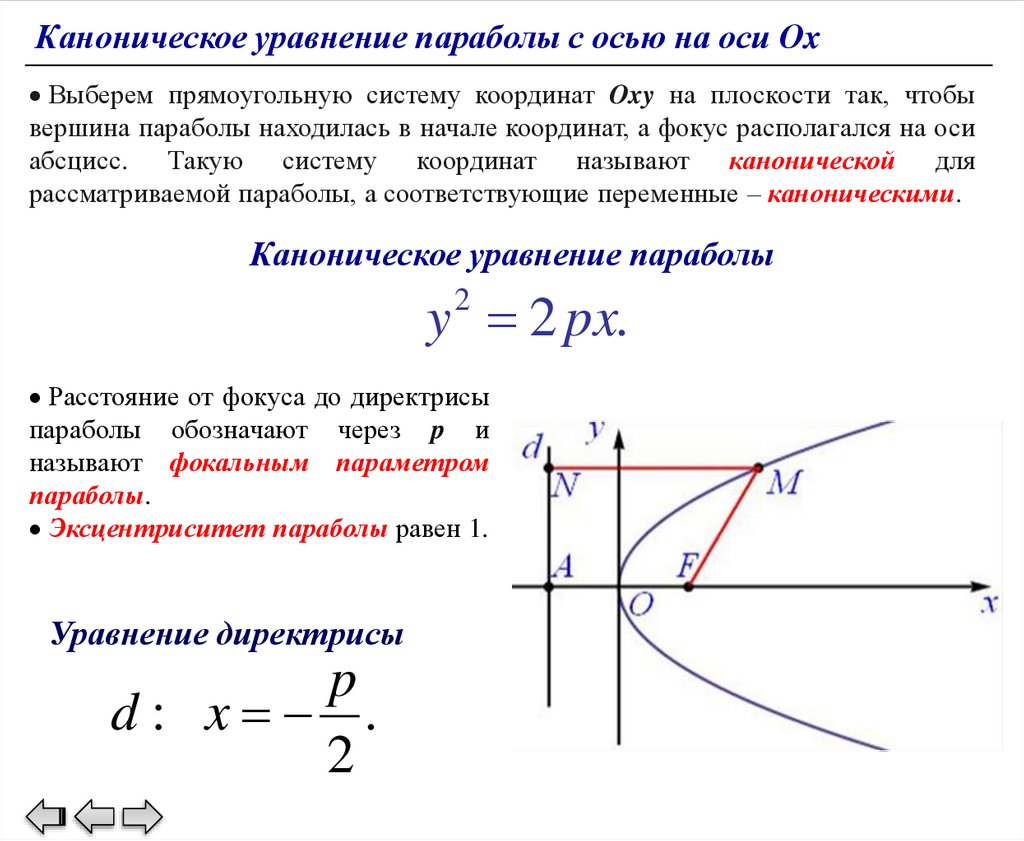
Каноническое уравнение параболы с осью на оси OxВыберем прямоугольную систему координат Oxy на плоскости так, чтобы
вершина параболы находилась в начале координат, а фокус располагался на оси
абсцисс. Такую систему координат называют канонической для
рассматриваемой параболы, а соответствующие переменные – каноническими.
Каноническое уравнение параболы
y 2 px.
2
Расстояние от фокуса до директрисы
параболы обозначают через p и
называют фокальным параметром
параболы.
Эксцентриситет параболы равен 1.
Уравнение директрисы
p
d: x .
2
30.
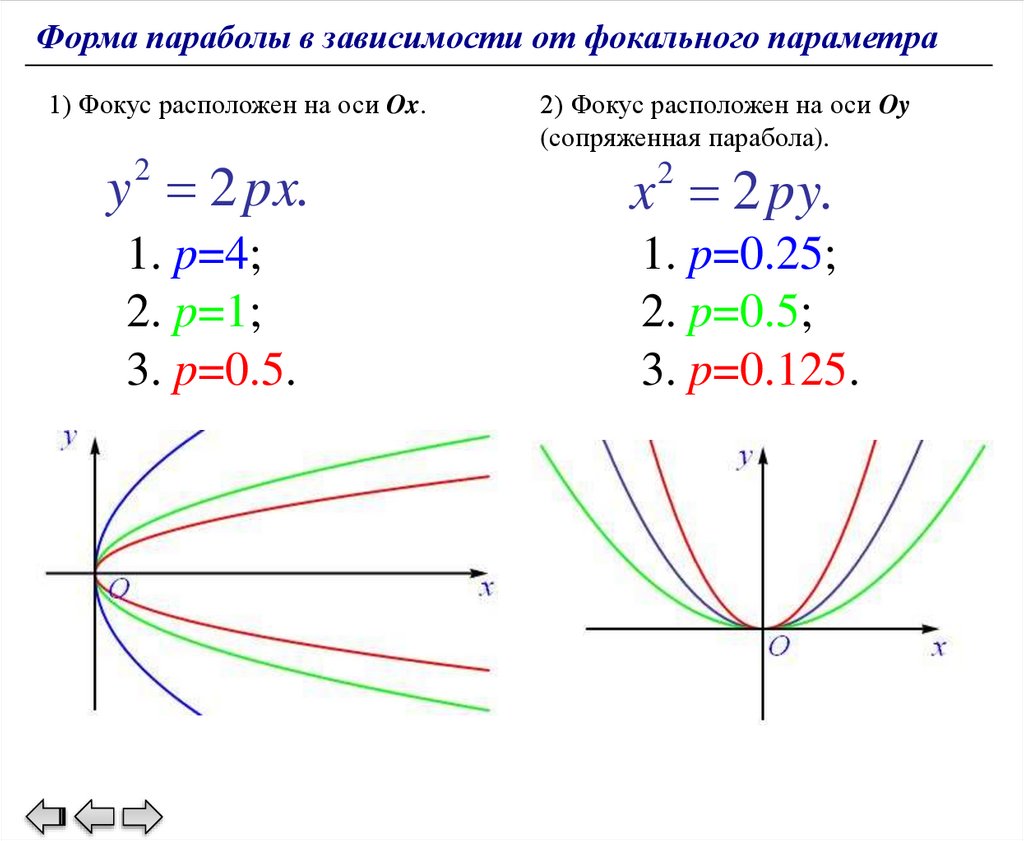
Форма параболы в зависимости от фокального параметра1) Фокус расположен на оси Ox.
y 2 px.
2) Фокус расположен на оси Oy
(сопряженная парабола).
2
x 2 py.
1. p=4;
2. p=1;
3. p=0.5.
1. p=0.25;
2. p=0.5;
3. p=0.125.
2
31.
Другие виды канонических уравнений параболы1) Фокус расположен на оси Ox.
y 2 px.
2
p
p
F ,0 , d : x .
2
2
2) Фокус расположен на оси Oy.
x 2 py.
2
p
p
F 0, , d : y .
2
2
32.
Оптическое свойство параболыЕсли в фокус параболы поместить источник света, то все световые лучи после
отражения от параболы будут параллельны оси параболы.
33.
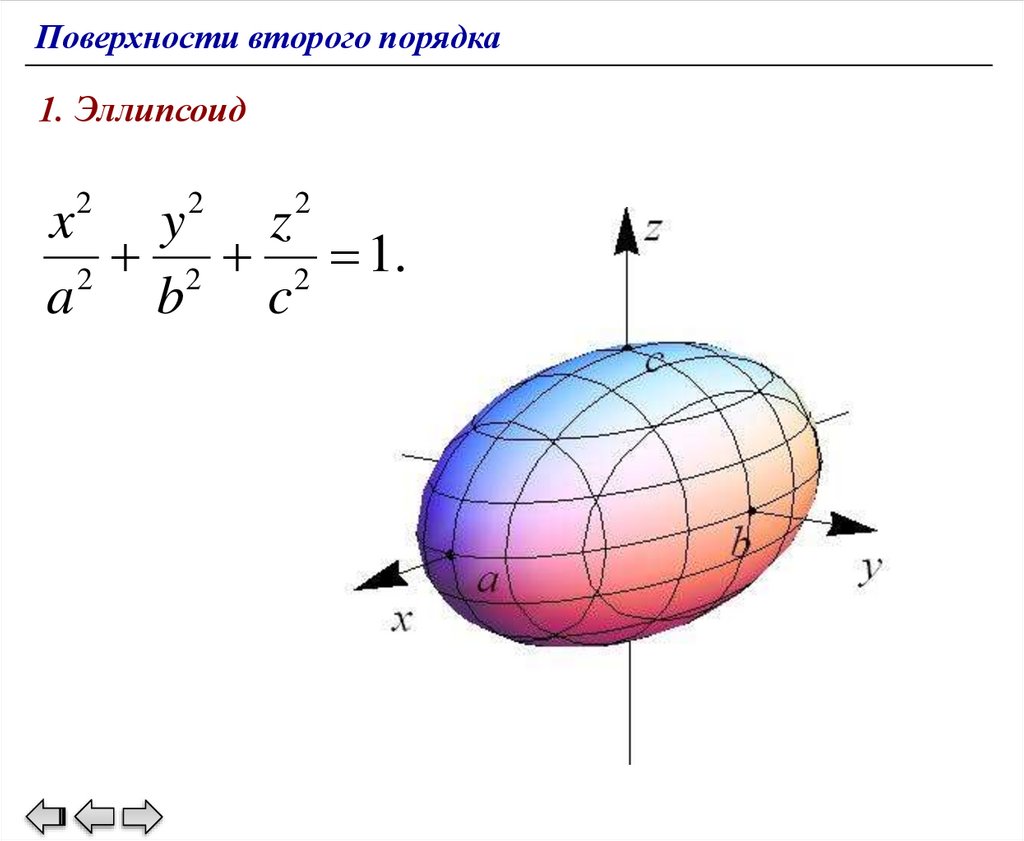
Поверхности второго порядка1. Эллипсоид
x2 y 2 z 2
2 2 1.
2
a
b
c
34.
Поверхности второго порядка2. Гиперболоид
а) однополостный
2
2
2
x
y
z
2 2 1;
2
a
b
c
б) двуполостный
2
2
2
x
y
z
2 2 1.
2
a
b
c
35.
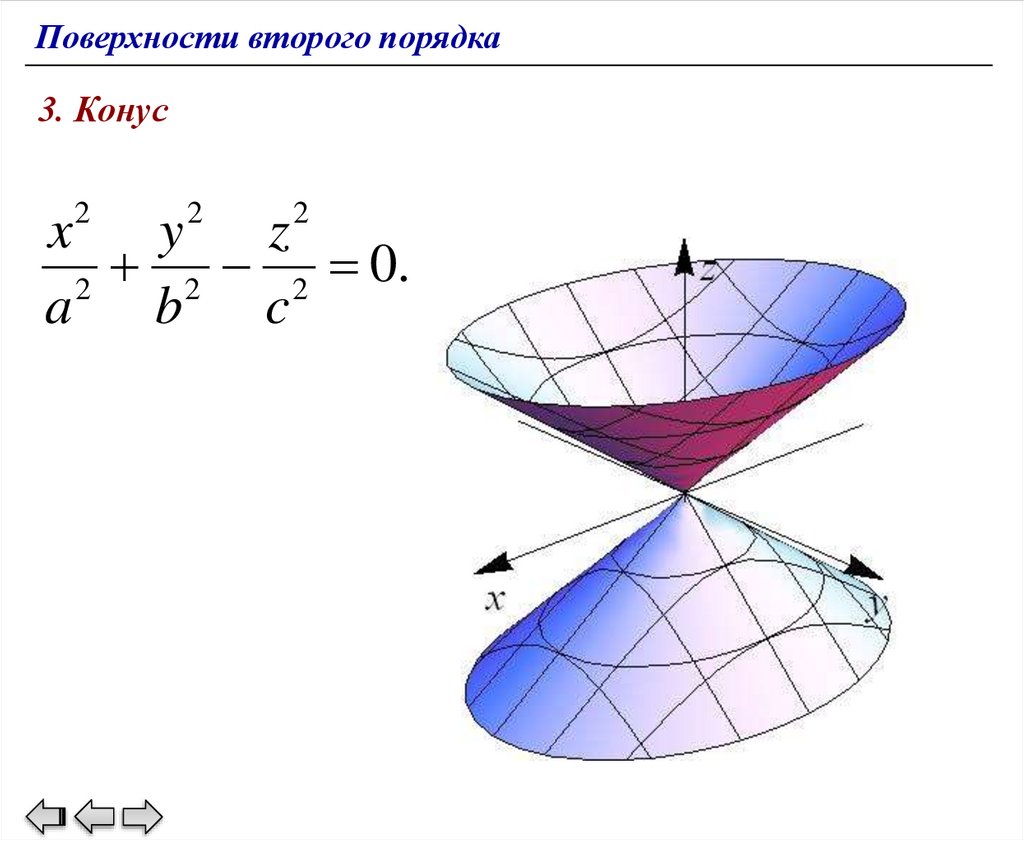
Поверхности второго порядка3. Конус
2
2
2
x
y
z
2 2 0.
2
a
b
c
36.
Поверхности второго порядка4. Параболоид
а) эллиптический
2
2
x
y
2 z;
2
a
b
б) гиперболический
2
2
x
y
2 z.
2
a b
37.
Поверхности второго порядка5. Цилиндр второго порядка
а) эллиптический
2
2
x
y
2 1;
2
a
b
б) гиперболический
2
2
x
y
2 1;
2
a
b
в) параболический
y 2 px.
2
38.
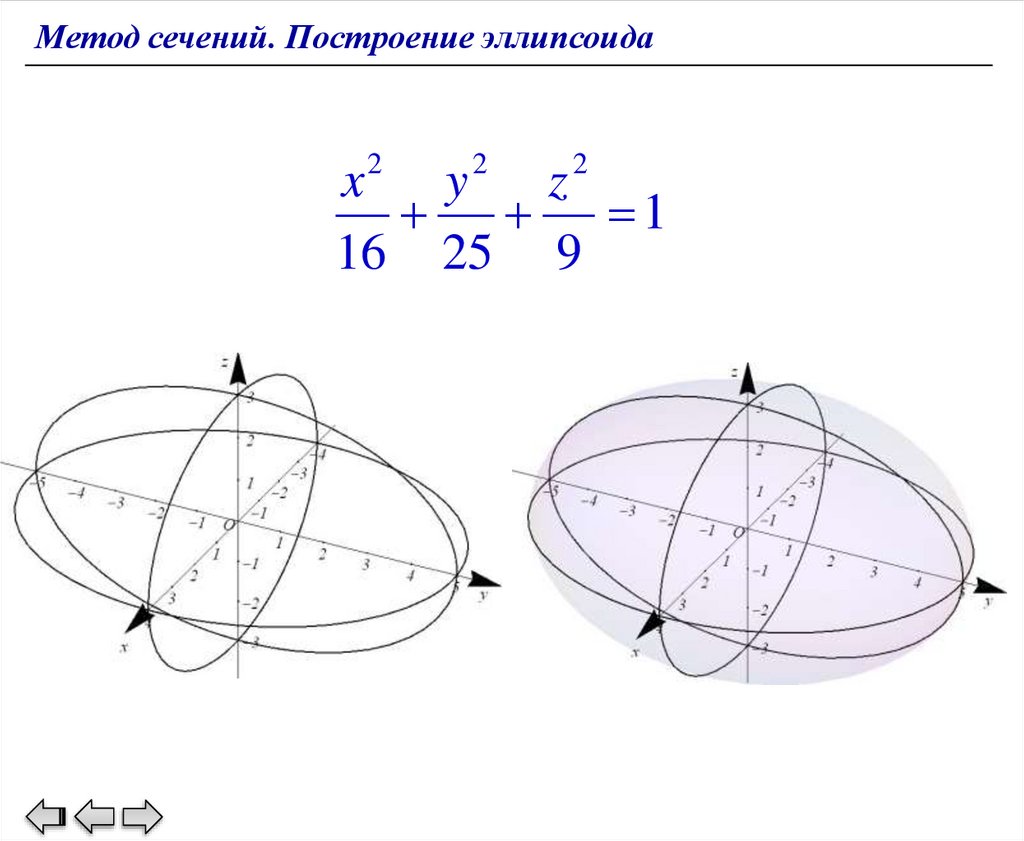
Метод сечений. Построение эллипсоида2
2
2
x
y
z
1
16 25 9
1. Сечение плоскостью yOz:
x 0,
2
y
z2
1.
25 9
39.
Метод сечений. Построение эллипсоида2
2
2
x
y
z
1
16 25 9
2. Сечение плоскостью xOz:
y 0,
2
x
z2
1.
16 9
40.
Метод сечений. Построение эллипсоида2
2
2
x
y
z
1
16 25 9
3. Сечение плоскостью xOy:
z 0,
2
x
y2
1.
16 25
41.
Метод сечений. Построение эллипсоидаx2 y2 z 2
1
16 25 9
42.
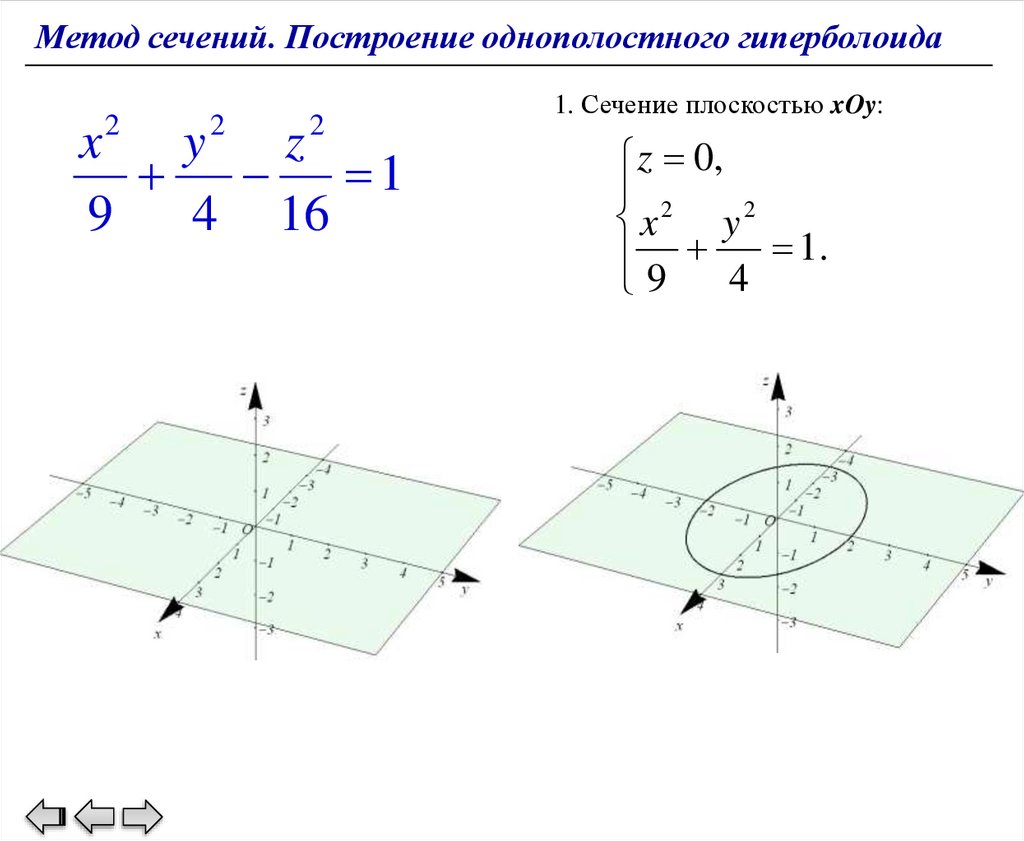
Метод сечений. Построение однополостного гиперболоида2
2
2
x
y
z
1
9
4 16
1. Сечение плоскостью xOy:
z 0,
2
x
y2
1.
4
9
43.
Метод сечений. Построение однополостного гиперболоида2
2
2
x
y
z
1
9
4 16
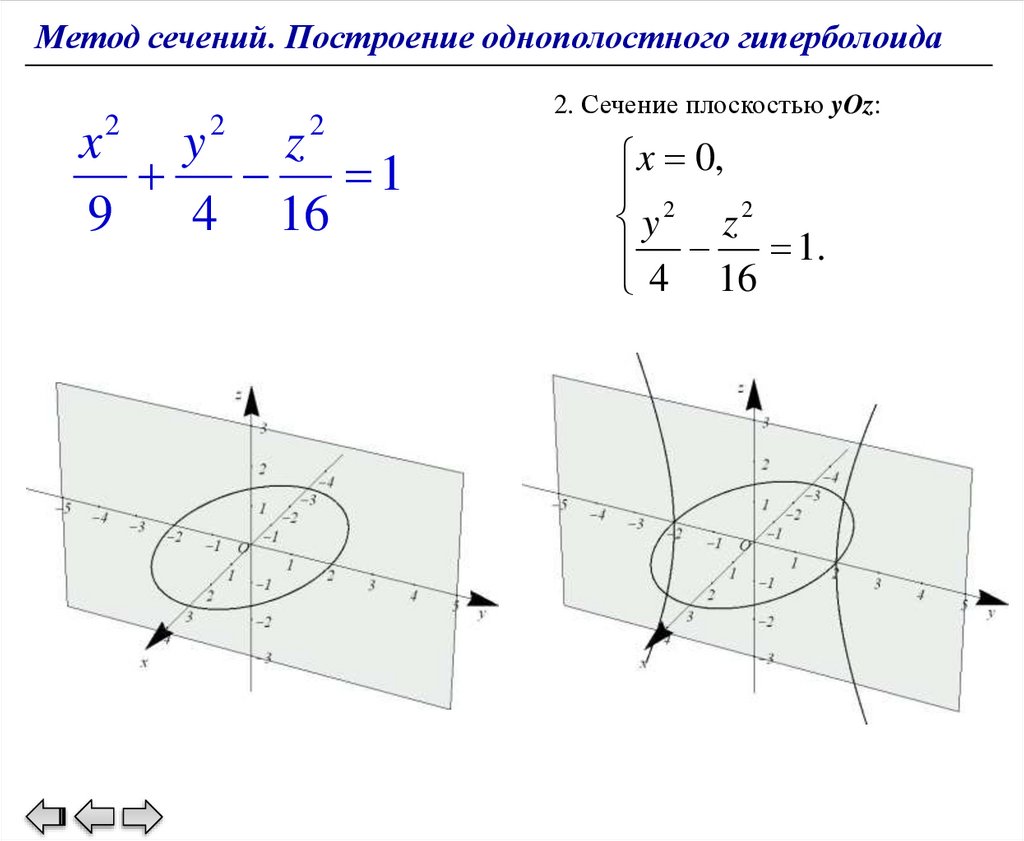
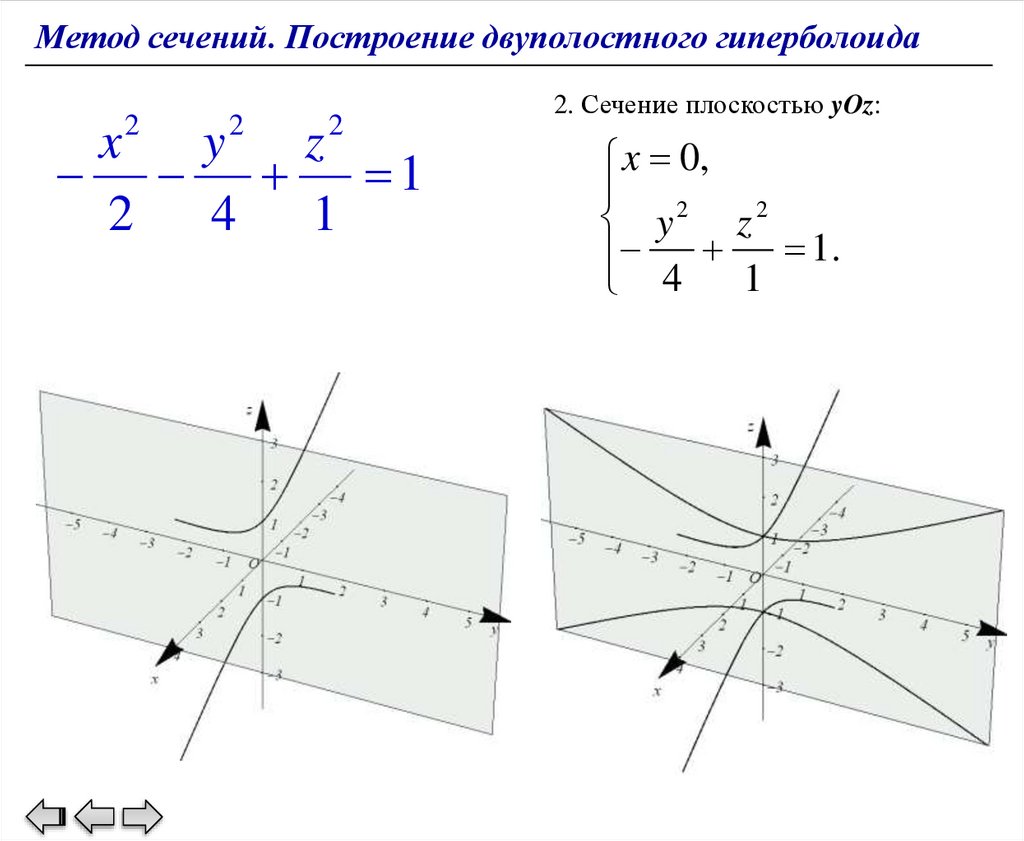
2. Сечение плоскостью yOz:
x 0,
2
y
z2
1.
4 16
44.
Метод сечений. Построение однополостного гиперболоида2
2
2
x
y
z
1
9
4 16
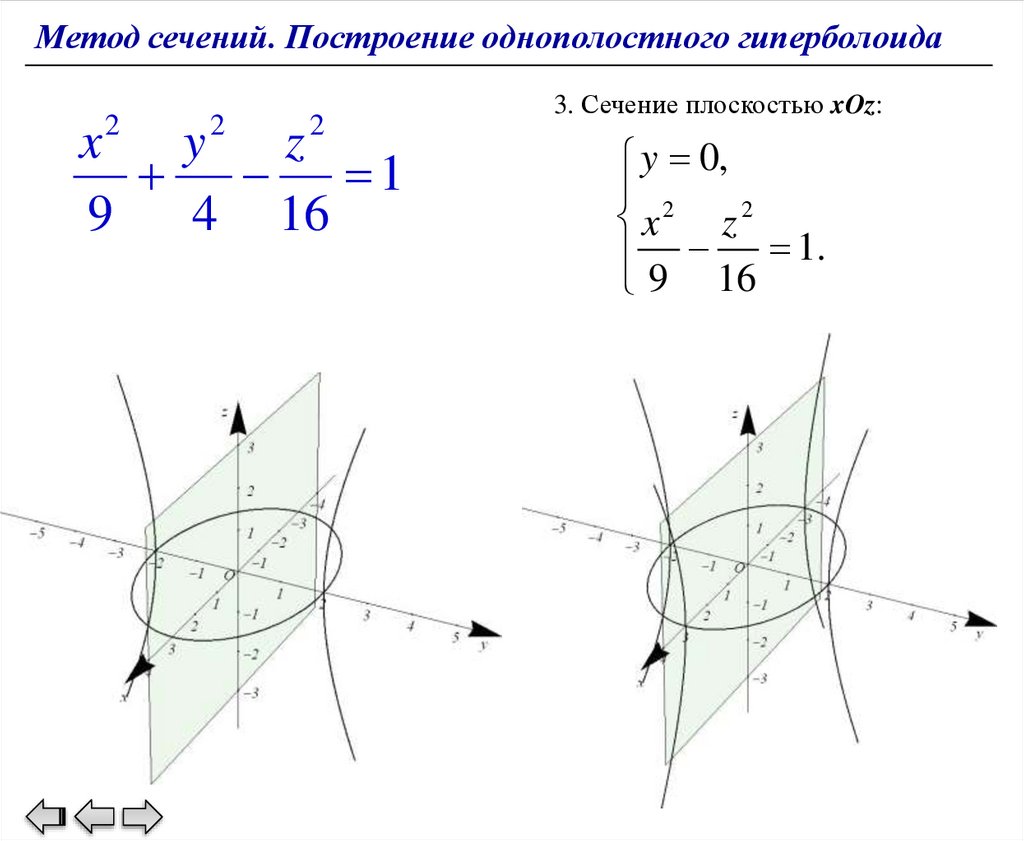
3. Сечение плоскостью xOz:
y 0,
2
x
z2
1.
9 16
45.
Метод сечений. Построение однополостного гиперболоида2
2
2
x
y
z
1
9
4 16
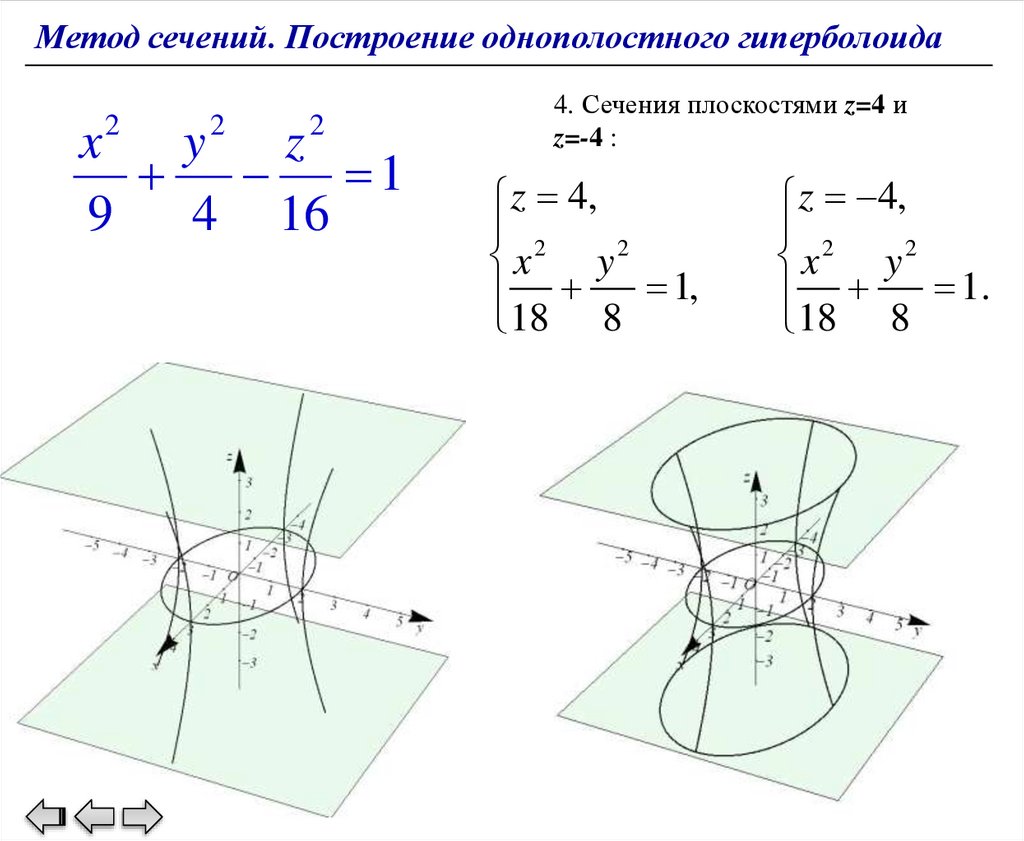
4. Сечения плоскостями z=4 и
z=-4 :
z 4,
2
x
y2
1,
18 8
z 4,
2
x
y2
1.
18 8
46.
Метод сечений. Построение однополостного гиперболоидаx2 y2 z 2
1
9
4 16
47.
Метод сечений. Построение двуполостного гиперболоида2
2
2
x
y
z
1
2 4 1
1. Сечение плоскостью xOz:
y 0,
2
x
z2
1.
2 1
48.
Метод сечений. Построение двуполостного гиперболоида2
2
2
x
y
z
1
2 4 1
2. Сечение плоскостью yOz:
x 0,
2
y
z2
1.
1
4
49.
Метод сечений. Построение двуполостного гиперболоида2
2
2
x
y
z
1
2 4 1
3. Сечения плоскостями z=3 и
z=-3 :
z 3,
2
x
y2
1,
16 32
z 3,
2
x
y2
1.
16 32
50.
Метод сечений. Построение двуполостного гиперболоидаx2 y2 z 2
1
2 4 1
51.
Пример 1Задание:
Привести уравнение эллипса параллельным переносом к
каноническому виду и построить эллипс в системе координат Oxy.
Указать:
1) канонический вид уравнения;
2) преобразование параллельного переноса, приводящее к каноническому виду;
3) полуоси, эксцентриситет, центр, вершины, фокусы, расстояния от точки
C 2 3 2 ,0 до фокусов;
4) для точки C проверить свойство, характеризующее эллипс как
геометрическое место точек.
16 x 2 y 2 64 x 4 y 52 0.
Решение:
Выделим в уравнении полные квадраты:
16( x 2 4 x) ( y 2 4 y) 52 0,
16 x 2 4 x 4 4 y 2 4 y 4 4 52 0,
16 x 2 y 2 16 0,
2
2
52.
16 x 2 4 x 4 4 y 2 4 y 4 4 52 0,16( x 2 4 x 4 4) y 2 4 y 4 4 52 0,
16 x 2 4 x 4 4 y 2 4 y 4 4 52 0,
53.
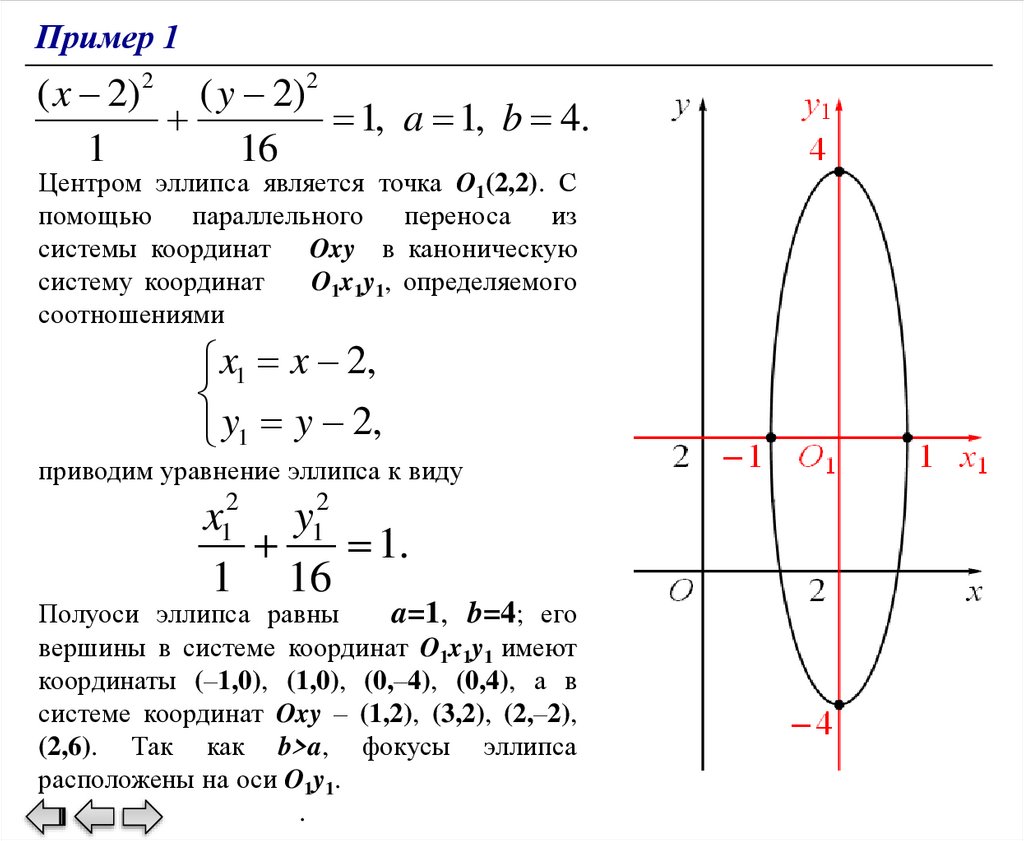
Пример 1( x 2)2 ( y 2)2
1, a 1, b 4.
1
16
Центром эллипса является точка O1(2,2). С
помощью параллельного переноса из
системы координат Oxy в каноническую
систему координат
O1x1y1, определяемого
соотношениями
x1 x 2,
y1 y 2,
приводим уравнение эллипса к виду
x12 y12
1.
1 16
Полуоси эллипса равны
a=1, b=4; его
вершины в системе координат O1x1y1 имеют
координаты (–1,0), (1,0), (0,–4), (0,4), а в
системе координат Oxy – (1,2), (3,2), (2,–2),
(2,6). Так как b>a, фокусы эллипса
расположены на оси O1y1.
.
54.
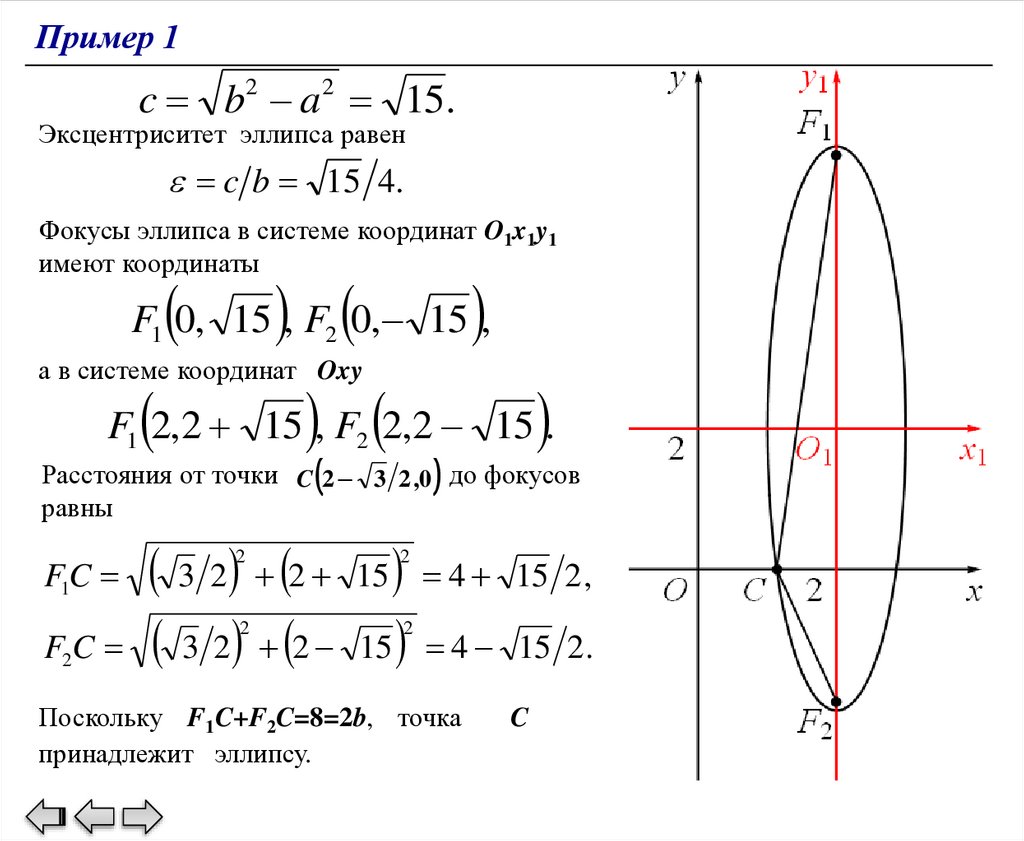
Пример 1c b2 a 2 15.
Эксцентриситет эллипса равен
c b 15 4.
Фокусы эллипса в системе координат O1x1y1
имеют координаты
F1 0, 15 , F2 0, 15 ,
а в системе координат Oxy
F1 2,2 15 , F2 2,2 15 .
Расстояния от точки C 2 3 2 ,0 до фокусов
равны
3 2 2 15 4 15 2 ,
F C 3 2 2 15 4 15 2.
F1C
2
2
2
2
2
Поскольку F1C+F2C=8=2b, точка
принадлежит эллипсу.
C
55.
Пример 2Задание: Привести уравнение гиперболы параллельным переносом к
каноническому виду и построить гиперболу в системе координат Oxy.
Указать:
1) канонический вид уравнения;
2) преобразование параллельного переноса, приводящее к каноническому виду;
3) полуоси, эксцентриситет, центр, вершины, фокусы, расстояния от точки
C 1 15 2 ,0 до фокусов, уравнения асимптот;
4) для точки C проверить свойство, характеризующее гиперболу как
геометрическое место точек.
4 x 2 5 y 2 8 x 20 y 11.
Решение:
Выделим в уравнении полные квадраты:
4( x 2 2 x) 5( y 2 4 y) 11,
4(( x 2 2 x 1) 1) 5(( y 2 4 y 4) 4) 11,
4( x 1)2 5( y 2)2 5,
56.
Пример 2( x 1)2 ( y 2)2
1.
54
1
Центром гиперболы является точка
О1(1,2). С помощью параллельного
переноса из системы координат Oxy в
каноническую систему координат
O1x1y1, определяемого соотношениями
x1 x 1,
y1 y 2,
приводим уравнение гиперболы к виду
x12 y12
1.
54 1
Полуоси гиперболы равны a 5 2 ,
b 1, ее вершины в системе координат
O1x1y1 имеют координаты (0,1), (0,–1),
а в системе координат Oxy – (1,3),
(1,1).
57.
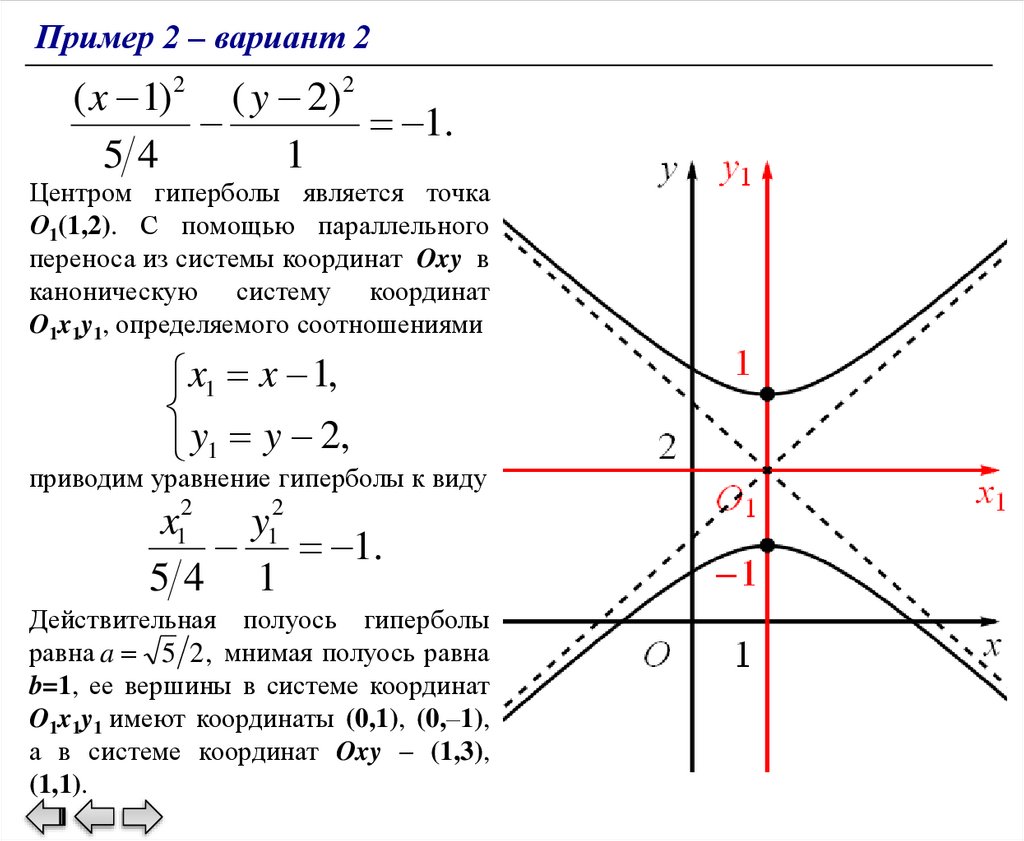
Пример 2 – вариант 2( x 1)2 ( y 2)2
1.
54
1
Центром гиперболы является точка
О1(1,2). С помощью параллельного
переноса из системы координат Oxy в
каноническую систему координат
O1x1y1, определяемого соотношениями
x1 x 1,
y1 y 2,
приводим уравнение гиперболы к виду
x12 y12
1.
54 1
Действительная полуось гиперболы
равна a 5 2 , мнимая полуось равна
b=1, ее вершины в системе координат
O1x1y1 имеют координаты (0,1), (0,–1),
а в системе координат Oxy – (1,3),
(1,1).
58.
Пример 2Асимптотами гиперболы являются
прямые
2
y1
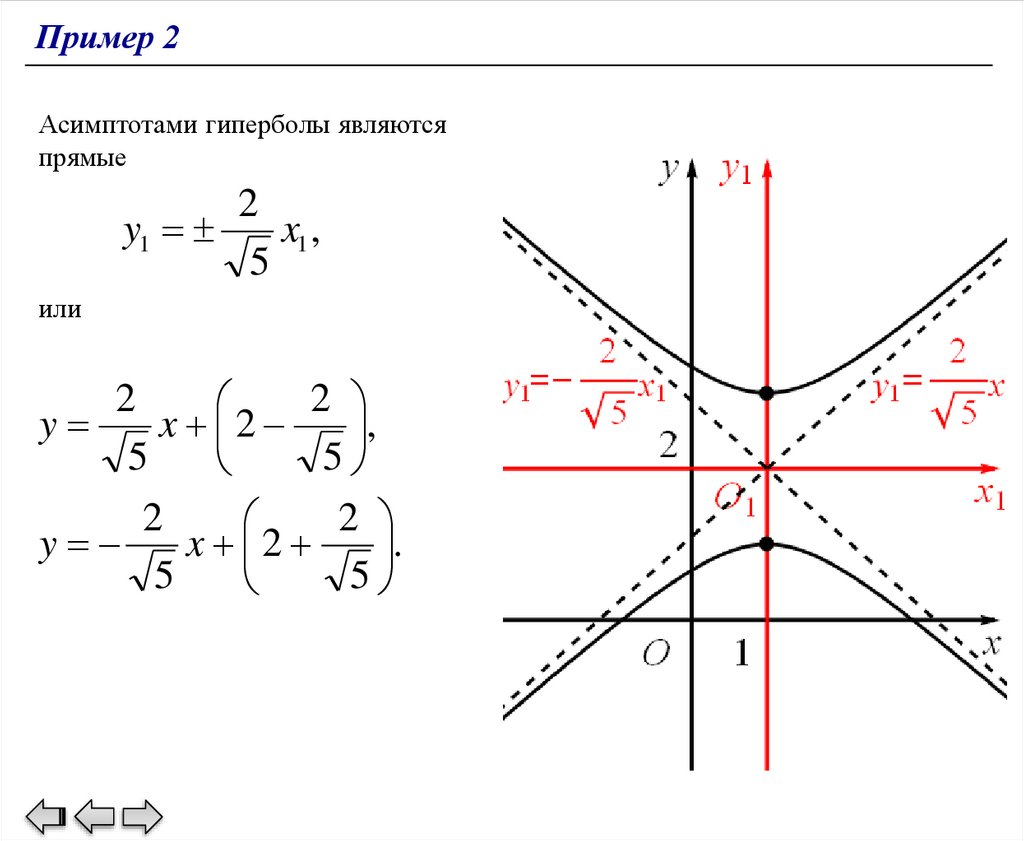
x1 ,
5
или
2
2
x 2
,
5
5
2
2
y
x 2
.
5
5
y
59.
Пример 2c b2 a 2 3 2.
Эксцентриситет гиперболы равен
c b 3 2.
Фокусы гиперболы в системе координат
O1x1y1 имеют координаты
F1 0, 3 2 , F2 0, 3 2 ,
а в системе координат Oxy – координаты
F1 1, 7 2 , F2 1,1 2 .
Расстояния от точки C 1 15 2 ,0 до
фокусов равны
15 2 7 2 4,
F C 15 2 1 2 2.
F1C
2
2
2
2
2
Поскольку |F1C-F2C|=2=2b, точка C
принадлежит гиперболе.
60.
Пример 3Задание: Привести уравнение параболы параллельным переносом к
каноническому виду и построить параболу в системе координат Oxy.
Указать:
1) канонический вид уравнения;
2) преобразование параллельного переноса, приводящее к каноническому виду;
3) параметр, вершину, фокус, уравнение директрисы, расстояния от точки
С(–3,1) до фокуса и директрисы;
4) для точки С проверить свойство, характеризующее параболу как
геометрическое место точек.
y 2 4 x 6 y 17 0.
Решение:
Выделим в уравнении полный квадрат по y:
(( y 2 6 y 9) 9) 4 x 17 0,
( y 3)2 4 x 8 0,
( y 3)2 2 2 ( x 2).
61.
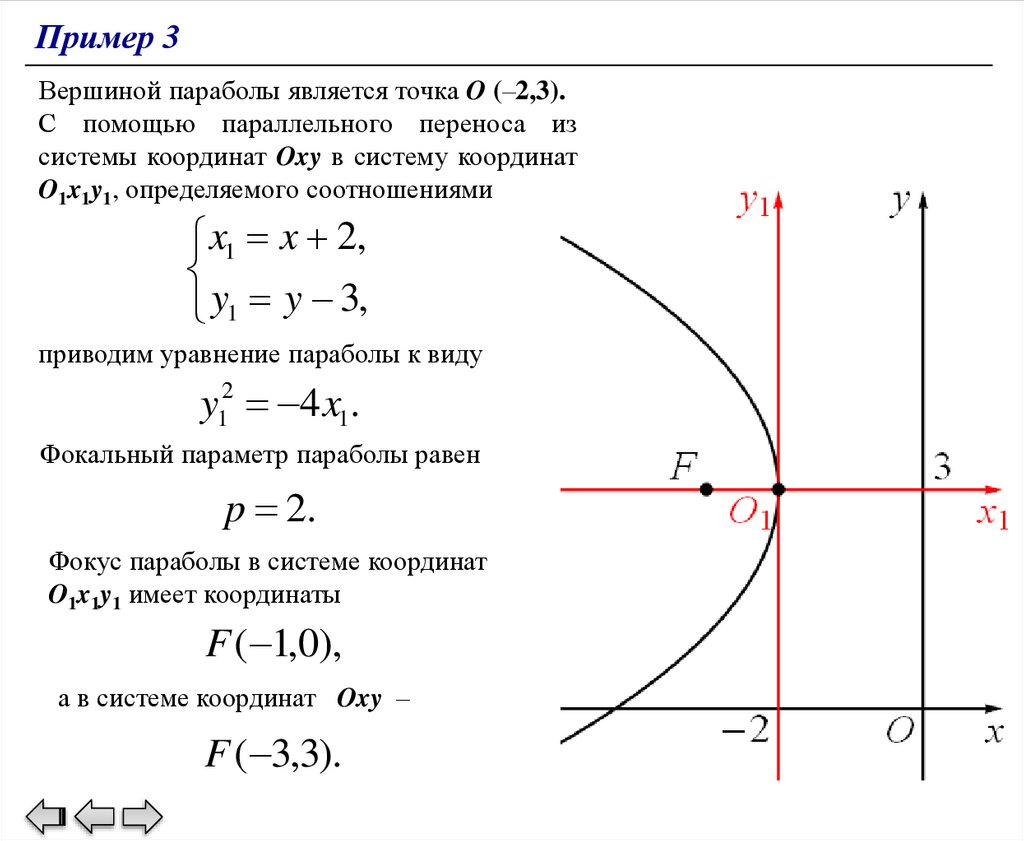
Пример 3Вершиной параболы является точка O (–2,3).
С помощью параллельного переноса из
системы координат Oxy в систему координат
O1x1y1, определяемого соотношениями
x1 x 2,
y1 y 3,
приводим уравнение параболы к виду
y12 4 x1.
Фокальный параметр параболы равен
p 2.
Фокус параболы в системе координат
O1x1y1 имеет координаты
F ( 1,0),
а в системе координат Oxy –
F ( 3,3).
62.
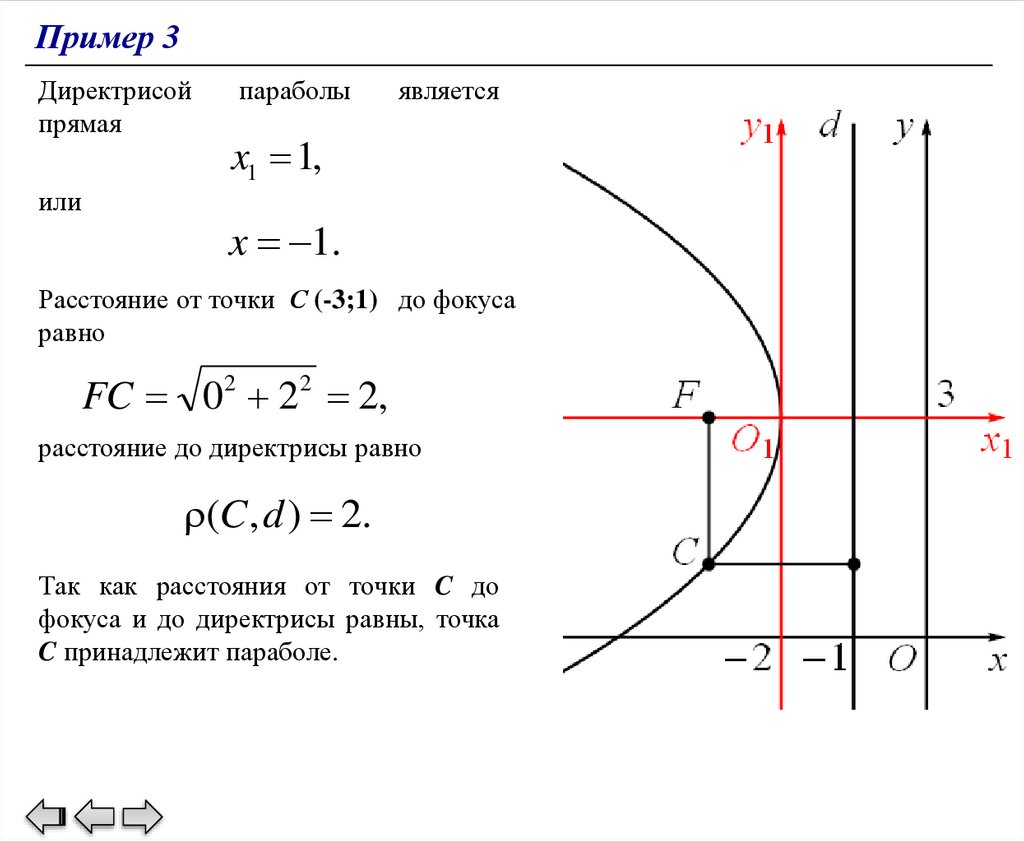
Пример 3Директрисой
прямая
или
параболы
является
x1 1,
x 1.
Расстояние от точки С (-3;1) до фокуса
равно
FC 02 22 2,
расстояние до директрисы равно
(C, d ) 2.
Так как расстояния от точки C до
фокуса и до директрисы равны, точка
C принадлежит параболе.
63.
Пример 4Задание: Найти уравнение эллипса, если известно, что он проходит через точку
С (0,–1), а его малая ось оканчивается вершинами A 3, 2 2 и B 3, 2 2 .
Решение:
Малая полуось эллипса равна b
AB – имеет координаты О1 (–3,–2).
1
AB 2 , а его центр – середина отрезка
2
64.
Пример 4Следовательно, уравнение эллипса имеет вид
( x 3)2 ( y 2)2
1,
2
a
2
где a – большая полуось эллипса.
Подставив в уравнение эллипса координаты точки C (0,–1), найдем a:
(0 3)2 ( 1 2)2
1,
2
a
2
9 1
,
2
a
2
a 2 18, a 0 a 3 2.
Итак, в исходной системе координат Oxy эллипс задается уравнением
( x 3)2 ( y 2)2
1.
18
2
65.
Пример 4С помощью параллельного переноса из системы координат
Oxy в
каноническую систему координат O1x1y1, определяемого соотношениями
x1 x 3,
y1 y 2,
приводим уравнение эллипса к каноническому виду
x12 y12
1.
18 2
a 3 2,
Полуоси эллипса равны
b 2 ; его вершины в системе
O1x1y1 имеют координаты
3 2,0 , 3 2,0 ,
0, 2 , 0, 2 ,
а в системе Oxy – координаты
3 3 2, 2 , 3 3 2, 2 ,
3, 2 2 , 3, 2 2 .
соответственно.
66.
Пример 4c a 2 b 2 4; эксцентриситет эллипса равен c a 2 2 3.
Фокусы эллипса в системе O1x1y1 имеют координаты F1 (4,0), F2 (–4,0), а в
системе координат Oxy – F1 (1,–2), F2 (–7,–2).
Расстояния от точки C (0,–1) до фокусов равны
1 2 2 1 2 2 ,
2
2
F2C 7 2 1 5 2 ,
F1C
F1C F2C 6 2 2a.
67.
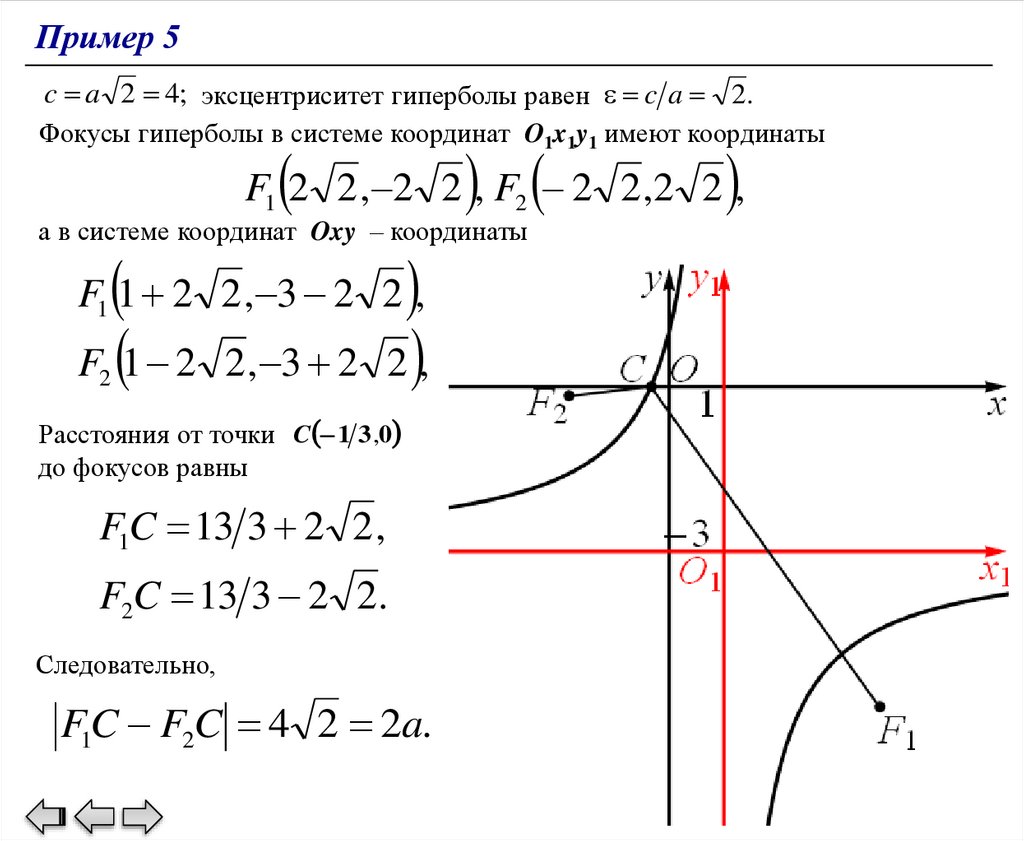
Пример 5Задание: Найти уравнение равносторонней гиперболы, имеющей асимптоту
x=1, пересекающей ось Ox в точке C (–1/3,0), а ось Oy – в точке A (0,1).
Решение:
Поскольку вертикальная асимптота гиперболы – прямая x=1,
гиперболы имеет вид
( x 1)( y y0 ) const .
Подставив в это уравнение координаты
точек C и A, получим
4 3 y0 1 1 y0 ,
откуда
4 3 y0 y0 1 y0 3.
Искомая
гипербола
уравнением
описывается
( x 1)( y 3) const.
Горизонтальной асимптотой гиперболы
является прямая y= –3. Подставив в
полученное
уравнение
гиперболы
координаты точки С, найдем const= –4.
уравнение
68.
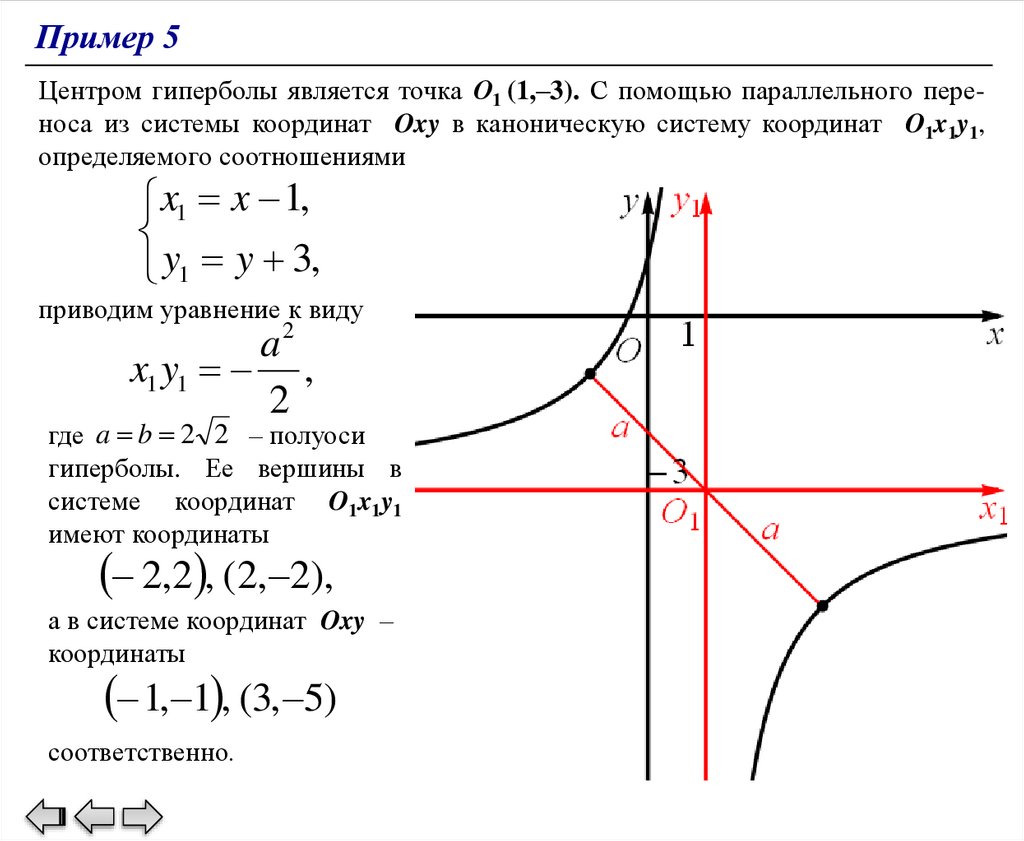
Пример 5Центром гиперболы является точка О1 (1,–3). С помощью параллельного переноса из системы координат Oxy в каноническую систему координат O1x1y1,
определяемого соотношениями
x1 x 1,
y1 y 3,
приводим уравнение к виду
a2
x1 y1 ,
2
где a b 2 2 – полуоси
гиперболы. Ее вершины в
системе координат O1x1y1
имеют координаты
2,2 , (2, 2),
а в системе координат Oxy –
координаты
1, 1 , (3, 5)
соответственно.
69.
Пример 5c a 2 4; эксцентриситет гиперболы равен c a 2.
Фокусы гиперболы в системе координат O1x1y1 имеют координаты
F1 2 2 , 2 2 , F2 2 2 ,2 2 ,
а в системе координат Oxy – координаты
F 1 2 2 , 3 2 2 ,
F1 1 2 2 , 3 2 2 ,
2
Расстояния от точки C 1 3 ,0
до фокусов равны
F1C 13 3 2 2 ,
F2C 13 3 2 2.
Следовательно,
F1C F2C 4 2 2a.
70.
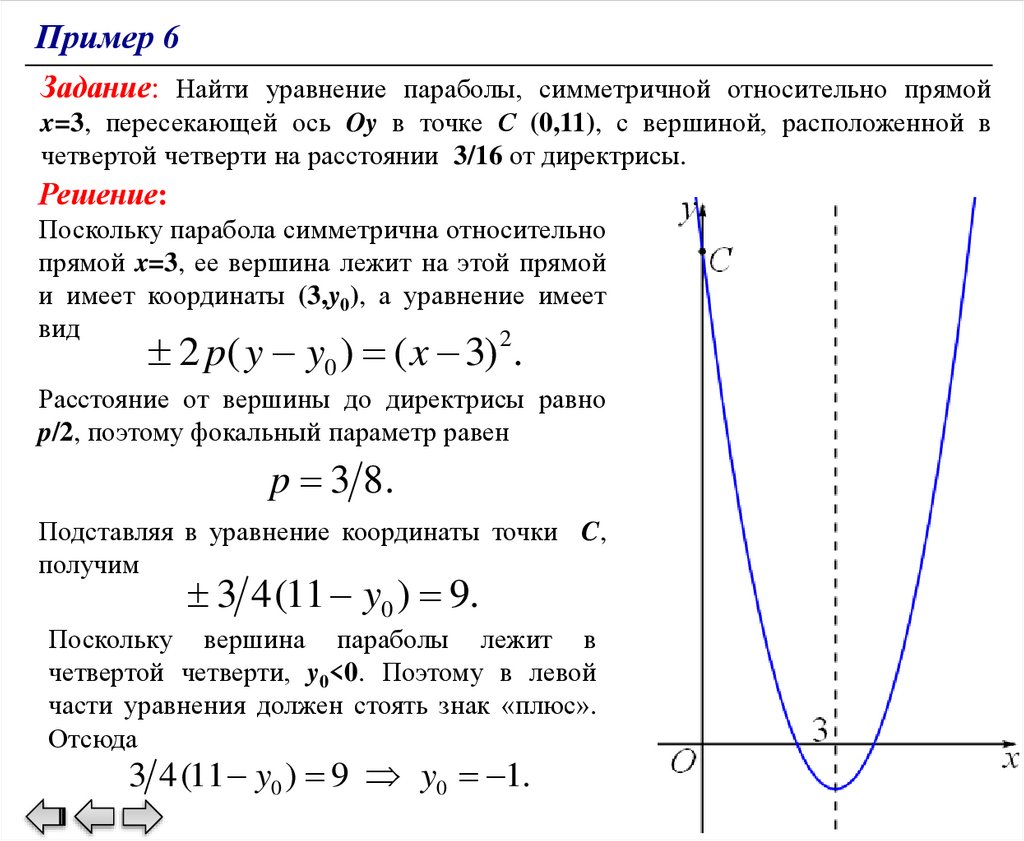
Пример 6Задание: Найти уравнение параболы, симметричной относительно прямой
x=3, пересекающей ось Oy в точке С (0,11), с вершиной, расположенной в
четвертой четверти на расстоянии 3/16 от директрисы.
Решение:
Поскольку парабола симметрична относительно
прямой x=3, ее вершина лежит на этой прямой
и имеет координаты (3,y0), а уравнение имеет
вид
2
2 p( y y0 ) ( x 3) .
Расстояние от вершины до директрисы равно
p/2, поэтому фокальный параметр равен
p 3 8.
Подставляя в уравнение координаты точки C,
получим
3 4 (11 y0 ) 9.
Поскольку вершина параболы лежит в
четвертой четверти, y0<0. Поэтому в левой
части уравнения должен стоять знак «плюс».
Отсюда
3 4 (11 y0 ) 9 y0 1.
71.
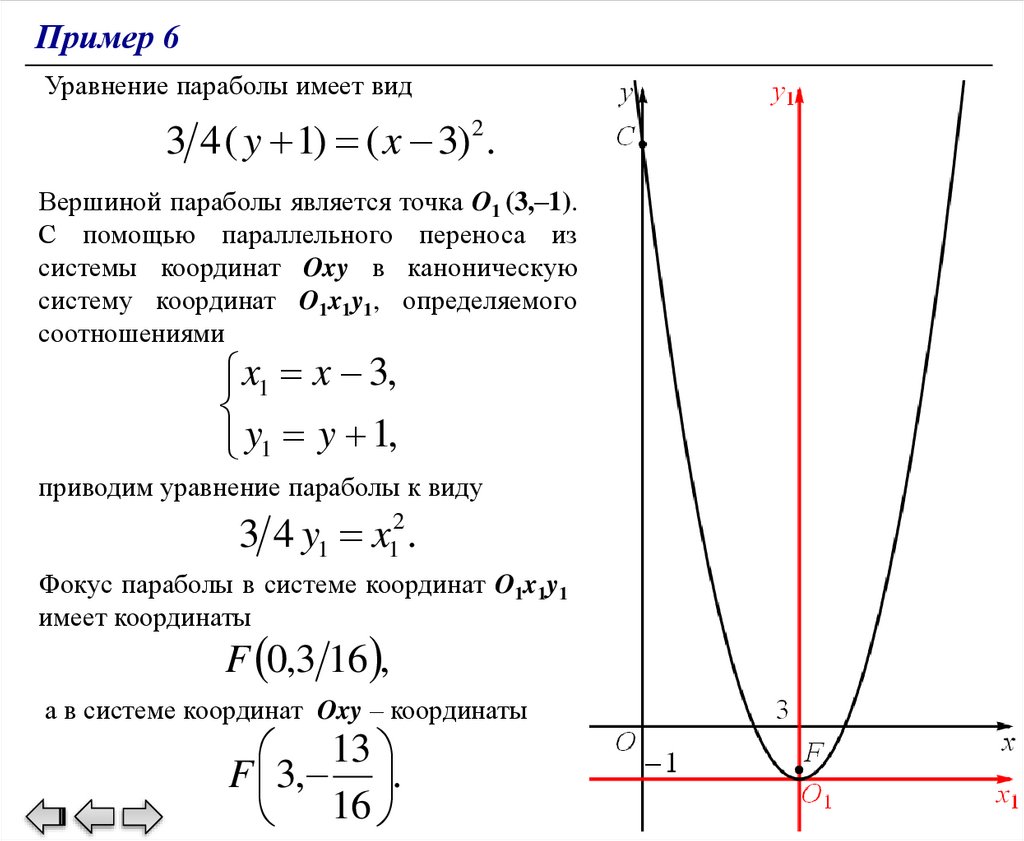
Пример 6Уравнение параболы имеет вид
3 4 ( y 1) ( x 3)2 .
Вершиной параболы является точка O1 (3,–1).
С помощью параллельного переноса из
системы координат Oxy в каноническую
систему координат O1x1y1, определяемого
соотношениями
x1 x 3,
y1 y 1,
приводим уравнение параболы к виду
3 4 y1 x12 .
Фокус параболы в системе координат O1x1y1
имеет координаты
F 0,3 16 ,
а в системе координат Oxy – координаты
13
F 3, .
16
72.
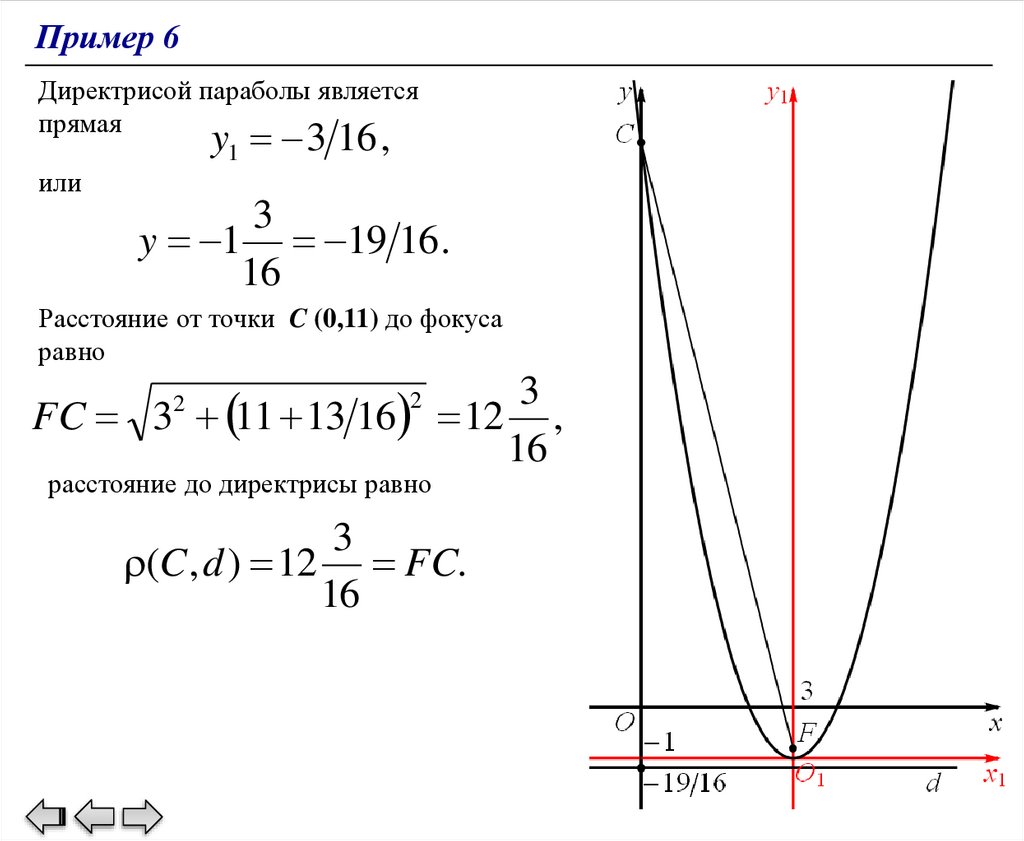
Пример 6Директрисой параболы является
прямая
y1 3 16 ,
или
3
y 1 19 16 .
16
Расстояние от точки C (0,11) до фокуса
равно
FC 32 11 13 16 12
2
расстояние до директрисы равно
3
(C , d ) 12 FC.
16
3
,
16
73.
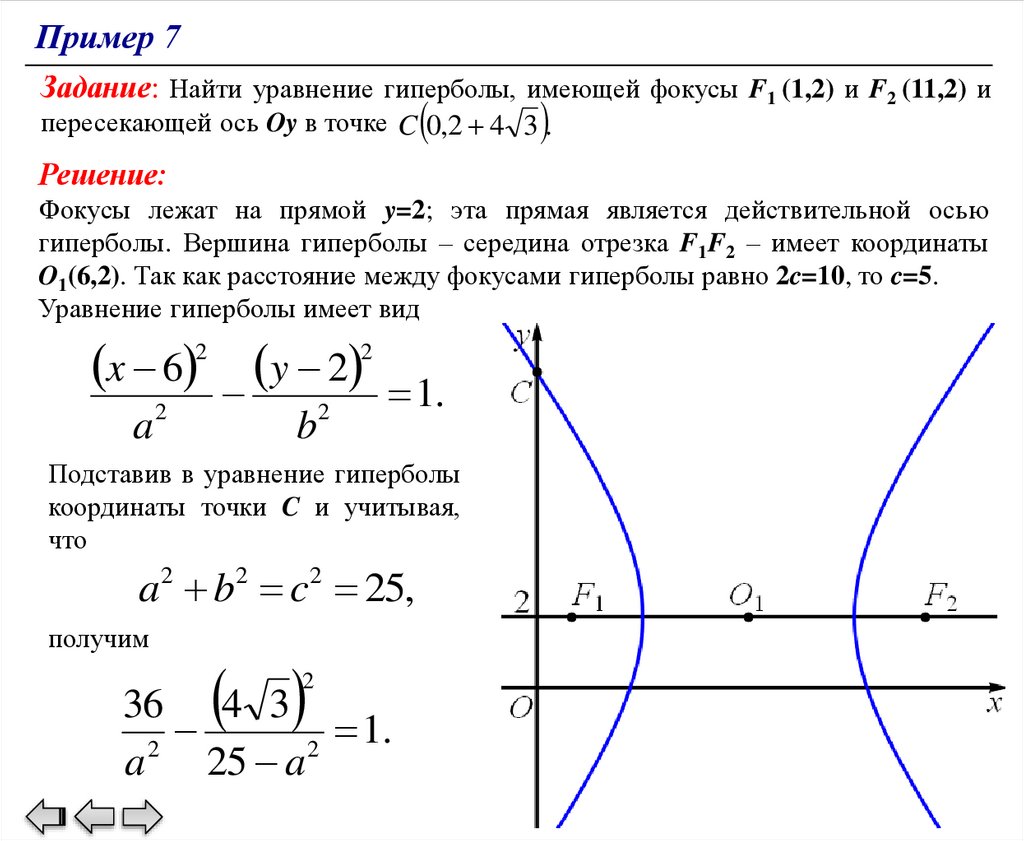
Пример 7Задание: Найти уравнение гиперболы, имеющей фокусы F1 (1,2) и F2 (11,2) и
пересекающей ось Oy в точке C 0,2 4 3 .
Решение:
Фокусы лежат на прямой y=2; эта прямая является действительной осью
гиперболы. Вершина гиперболы – середина отрезка F1F2 – имеет координаты
O1(6,2). Так как расстояние между фокусами гиперболы равно 2c=10, то c=5.
Уравнение гиперболы имеет вид
x 6 2 y 2 2 1.
a2
b2
Подставив в уравнение гиперболы
координаты точки C и учитывая,
что
a2 b2 c2 25,
получим
2
36 4 3
1.
2
2
a 25 a
74.
Пример 7Обозначим a2=t, 0<t<25, тогда
36
48
1 36(25 t ) 48t t (25 t )
t 25 t
t 100,
2
t 109t 900 0
t 9, a 3.
t 9,
Полуоси гиперболы равны
a 3, b 4.
Уравнение гиперболы имеет вид
x 6 2 y 2 2 1.
9
16
75.
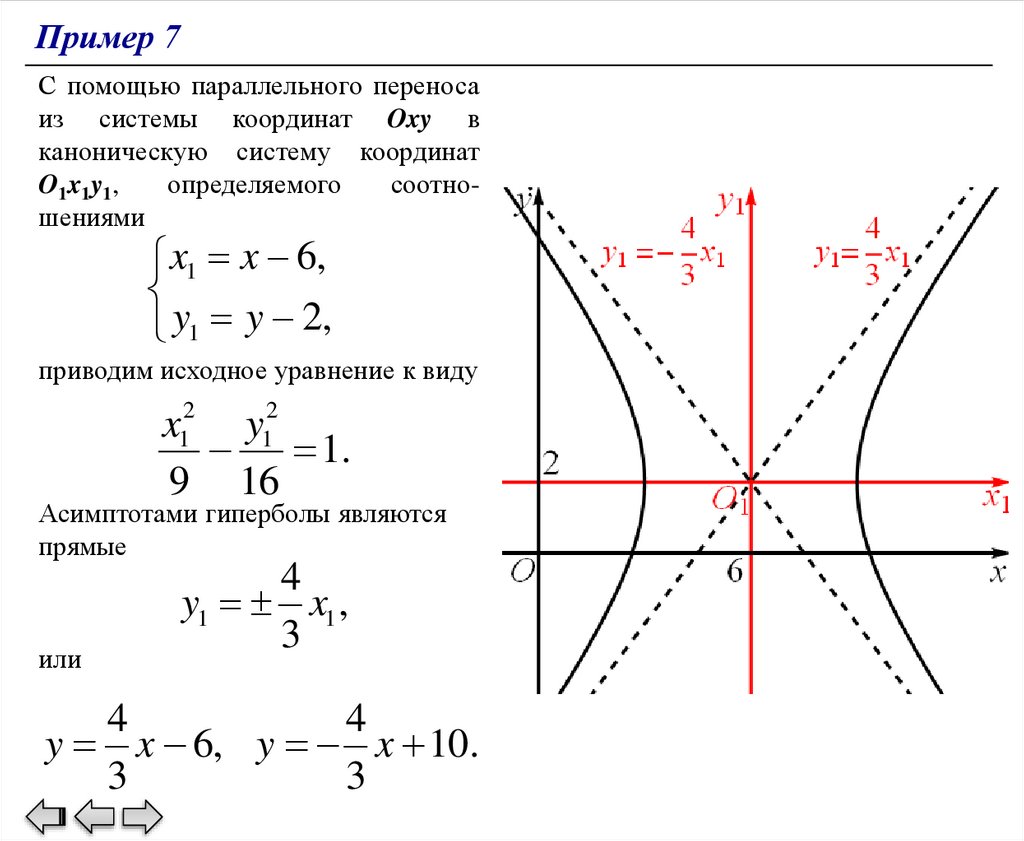
Пример 7С помощью параллельного переноса
из системы координат Oxy в
каноническую систему координат
O1x1y1,
определяемого
соотношениями
x1 x 6,
y1 y 2,
приводим исходное уравнение к виду
x12 y12
1.
9 16
Асимптотами гиперболы являются
прямые
или
4
y1 x1 ,
3
4
4
y x 6, y x 10.
3
3
76.
Пример 7Эксцентриситет гиперболы равен c a 5 3.
Фокусы гиперболы в системе координат O1x1y1 имеют координаты
F1 5,0 , F2 5,0 .
Вершины
гиперболы
в
системе координат O1x1y1
имеют координаты
3,0 , 3,0 ,
а в системе координат Oxy –
3,2 , 9,2 .
Расстояния от точки C 0,2 4 3
до фокусов равны
F C 11 4 3 13,
2
F1C 1 4 3 7,
2
2
2
2
F1C F2C 6 2a.
77.
Пример 8Задание: Указать преобразование параллельного переноса, приводящее данное
уравнение поверхности к каноническому виду, канонический вид уравнения
поверхности и тип поверхности. Построить поверхность в канонической системе
координат.
2 x2 4 y 2 z 2 4 x 16 y 4 z 18 0.
Решение:
Выделим в уравнении полные квадраты по каждой из переменных:
2 x 2 2 x 1 1 4 y 2 4 y 4 4
z 2 4 z 4 4 18 0,
2 ( x 1)2 4( y 2)2 ( z 2)2 4 0,
( x 1) 2 ( y 2) 2 ( z 2) 2
1.
2
1
4
78.
Пример 8С помощью параллельного переноса в систему координат O1x1y1z1 с центром
O1 (1,–2,2), определяемого соотношениями
x1 x 1,
y1 y 2,
z z 2,
1
приводим уравнение к каноническому
виду
x12 y12 z12
1.
2
1
4
Это уравнение описывает двуполостный
гиперболоид.
79.
Пример 9Задание: Указать преобразование параллельного переноса, приводящее данное
уравнение поверхности к каноническому виду, канонический вид уравнения
поверхности и тип поверхности. Построить поверхность в канонической системе
координат.
2 y 2 5 z 2 10 x 4 y 40 z 102 0.
Решение:
Выделим в уравнении полные квадраты по каждой из переменных:
2(( y 2 2 y 1) 1) 5(( z 2 8z 16) 16) 10 x 102 0,
2 ( y 1)2 5( z 4)2 10 x 20 0,
( y 1)2 ( z 4)2
x 2.
5
2
80.
Пример 9С помощью параллельного переноса в систему координат O1x1y1z1 с центром
O1 (2,–1,–4), определяемого соотношениями
x1 x 2,
y1 y 1,
z z 4,
1
приводим уравнение к каноническому
виду
y12 z12
x1.
5 2
Это уравнение описывает эллиптический параболоид.
81.
Пример 10Задание: Указать преобразование параллельного переноса, приводящее данное
уравнение поверхности к каноническому виду, канонический вид уравнения
поверхности и тип поверхности. Построить поверхность в канонической системе
координат.
9 x 2 18 y 2 2 z 2 36 x 12 z 36 0.
Решение:
Выделим в уравнении полные квадраты по каждой из переменных:
9(( x 2 4 x 4) 4) 18 y 2 2(( z 2 6 z 9) 9) 36 0,
9( x 2)2 18 y 2 2( z 3)2 18 0,
( x 2)2 y 2 ( z 3)2
1.
2
1
9
82.
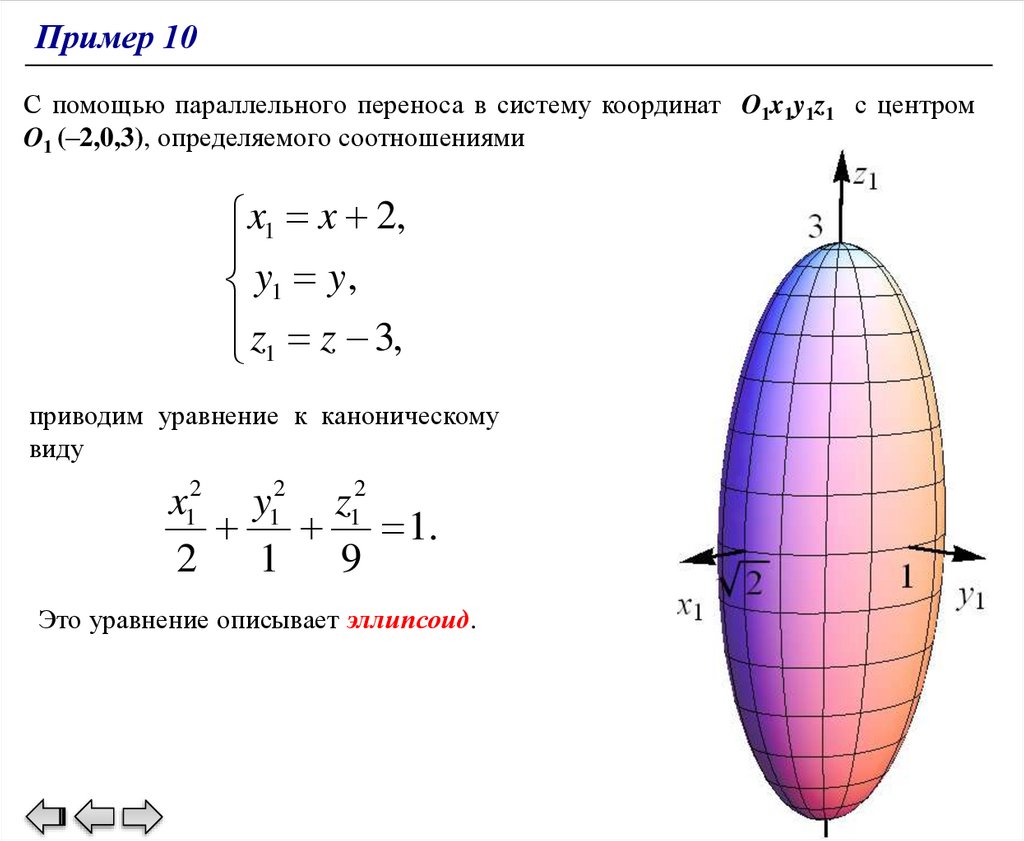
Пример 10С помощью параллельного переноса в систему координат O1x1y1z1 с центром
O1 (–2,0,3), определяемого соотношениями
x1 x 2,
y1 y,
z z 3,
1
приводим уравнение к каноническому
виду
x12 y12 z12
1.
2 1 9
Это уравнение описывает эллипсоид.
83.
Пример 11Задание: Указать преобразование параллельного переноса, приводящее данное
уравнение поверхности к каноническому виду, канонический вид уравнения
поверхности и тип поверхности. Построить поверхность в канонической системе
координат.
y2 4 x 4 y 0.
Решение:
Выделим в уравнении полный квадрат по переменной y:
( y 2)2 4 x 4 0,
( y 2)2 4( x 1).
84.
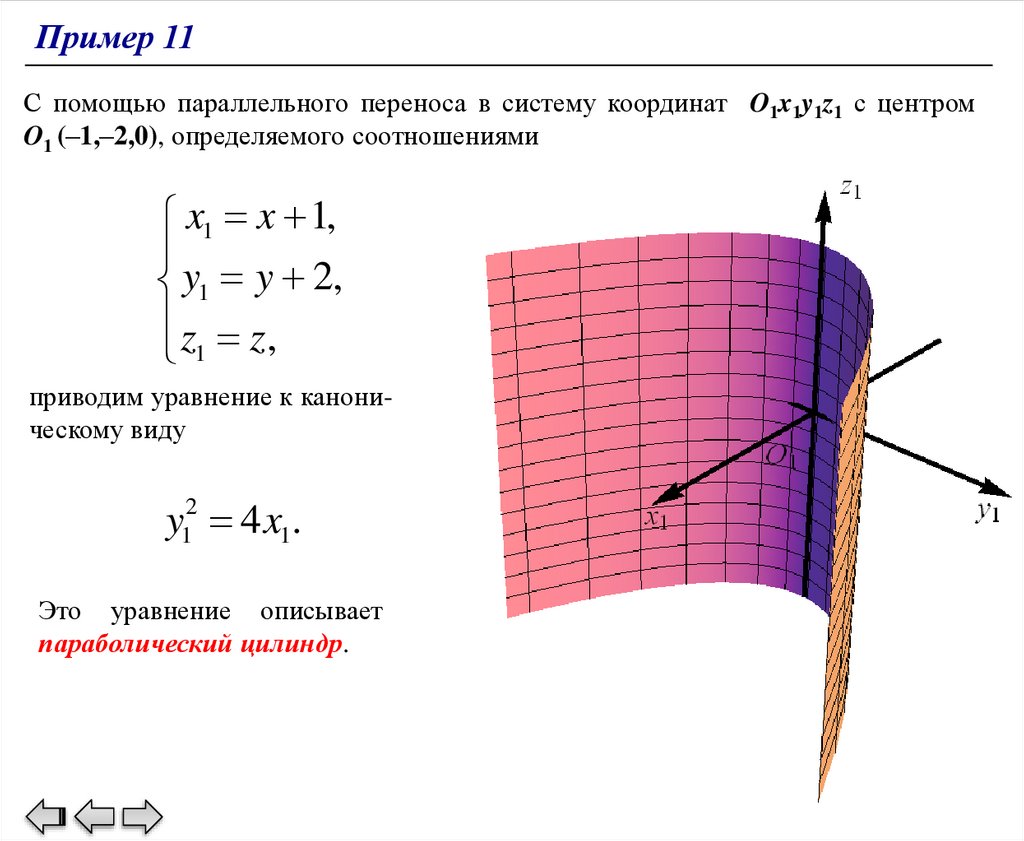
Пример 11С помощью параллельного переноса в систему координат O1x1y1z1 с центром
O1 (–1,–2,0), определяемого соотношениями
x1 x 1,
y1 y 2,
z z,
1
приводим уравнение к каноническому виду
y12 4 x1.
Это уравнение описывает
параболический цилиндр.
85.
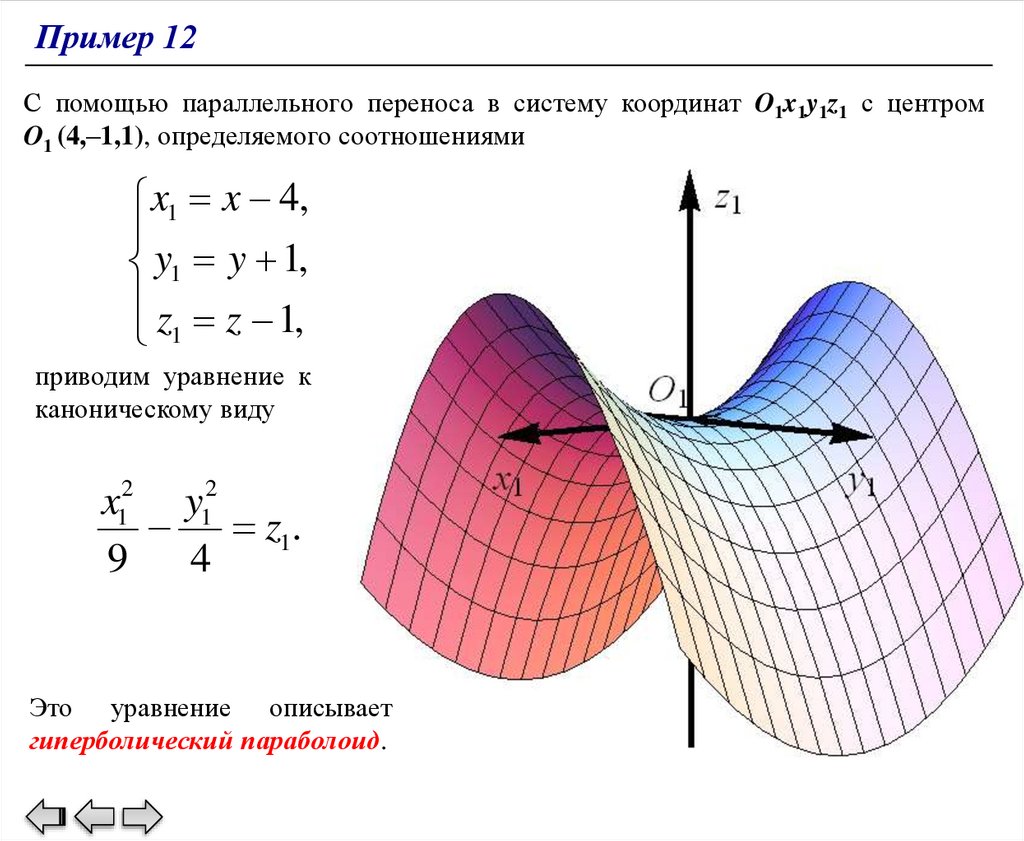
Пример 12Задание: Указать преобразование параллельного переноса, приводящее данное
уравнение поверхности к каноническому виду, канонический вид уравнения
поверхности и тип поверхности. Построить поверхность в канонической системе
координат.
4 x 2 9 y 2 32 x 18 y 36 z 91 0.
Решение:
Выделим в уравнении полные квадраты по каждой из переменных:
4(( x 2 8x 16) 16) 9(( y 2 2 y 1) 1) 36 z 91 0,
4( x 4)2 9( y 1)2 36( z 1) 0,
( x 4)2 ( y 1)2
z 1.
9
4
86.
Пример 12С помощью параллельного переноса в систему координат O1x1y1z1 с центром
O1 (4,–1,1), определяемого соотношениями
x1 x 4,
y1 y 1,
z z 1,
1
приводим уравнение к
каноническому виду
x12 y12
z1.
9
4
Это уравнение описывает
гиперболический параболоид.
87.
Пример 13Задание: Привести уравнение кривой второго порядка ортогональным
преобразованием и параллельным переносом к каноническому виду, указав
преобразования перехода от исходной прямоугольной системы координат Oxy к
полученной системе O2x2y2. Начертить кривую на плоскости Oxy, изобразив на
чертеже каноническую систему координат O2x2y2.
5 x 2 6 xy 5 y 2 20 2 x 12 2 y 24 0.
Решение:
В матричном виде уравнение этой кривой второго порядка имеет вид
X T AX C T X 24 0,
где
5 3
A
,
3 5
20 2
. ,
C
12 2
Квадратичная форма имеет вид
x
X .
y
X T AX 5x 2 6 xy 5 y 2 .
88.
Пример 13Найдём собственные числа и собственные векторы матрицы А квадратичной
T
2
2
формы X AX 5x 6 xy 5 y .
5
3
3
5
2 10 16 0,
Собственному значению λ1=2
соответствует
единичный
собственный вектор
1 1
.
e1
2 1
Собственному значению λ2=8
соответствует
единичный
собственный вектор
1 1
.
e2
2 1 .
1 2,
2 8.
89.
Пример 13Матрица ортогонального преобразования, приводящего квадратичную форму к
каноническому виду, составлена из столбцов координат собственных векторов.
Это преобразование является поворотом.
1
U 2
1
2
1
2 1 1 1 ,
1
2 1 1
2
det U 1.
Этому ортогональному преобразованию соответствует линейная замена
переменных X UX 1
x1
x
U ,
y
y1
1
1
x
x1
y1 ,
2
2
y 1 x 1 y . .
1
1
2
2
90.
Пример 13После подстановки x и y в уравнение кривой получаем уравнение с
квадратичной формой канонического вида
2
1
1 1
1
1
1
5
x1
y1 6
x1
y1
x1
y1
2
2 2
2
2
2
2
1
1
5
x1
y1
2
2
1
1
1
1
20 2
x1
y1 12 2
x1
y1 24 0,
2
2
2
2
5 2
5 2
5
5
3 x1 5 5 x1 y1 3 y1
2
2
2
2
20 12 x1 20 12 y1 24 0,
2 x12 8 y12 8x1 32 y1 24 0.
91.
Пример 13Отметим, что канонический вид квадратичной формы мы можем записать сразу
по известным собственным числам
5 x 2 6 xy 5 y 2 1 x12 2 y12 2 x12 8 y12 .
Порядок следования собственных чисел соответствует порядку собственных
векторов в матрице ортогонального преобразования – матрице перехода между
ортонормированными базисами систем координат Oxy и Ox1y1.
Линейные слагаемые преобразуются следующим образом.
Поскольку C T X C T UX 1 , то вектор-строка коэффициентов при линейных
слагаемых равен
1
CU
20 2
2
T
1 1
12 2
8 32 .
1 1
Свободный член останется прежним.
В результате уравнение поверхности в системе координат Ox1y1 принимает вид
2 x12 8 y12 8 x1 32 y1 24 0.
После деления обеих частей уравнения на 2 получаем
x12 4 y12 4 x1 16 y1 12 0.
.
92.
Пример 13По каждой из переменных выделяем полный квадрат:
x 4x 4 4 4 y 4 y 4 4 12 0,
2
1
2
1
1
1
x1 2 2 4 y1 2 2 8. 0.
Преобразование параллельного переноса
x2 x1 2,
y2 y1 2
приводит к уравнению в системе координат O2x2y2, началом которой является
точка O2 (–2,2)
x22 4 y22 8.
Разделив обе части уравнения на 8, получаем каноническое уравнение эллипса
x22 y22
1.
8
2
93.
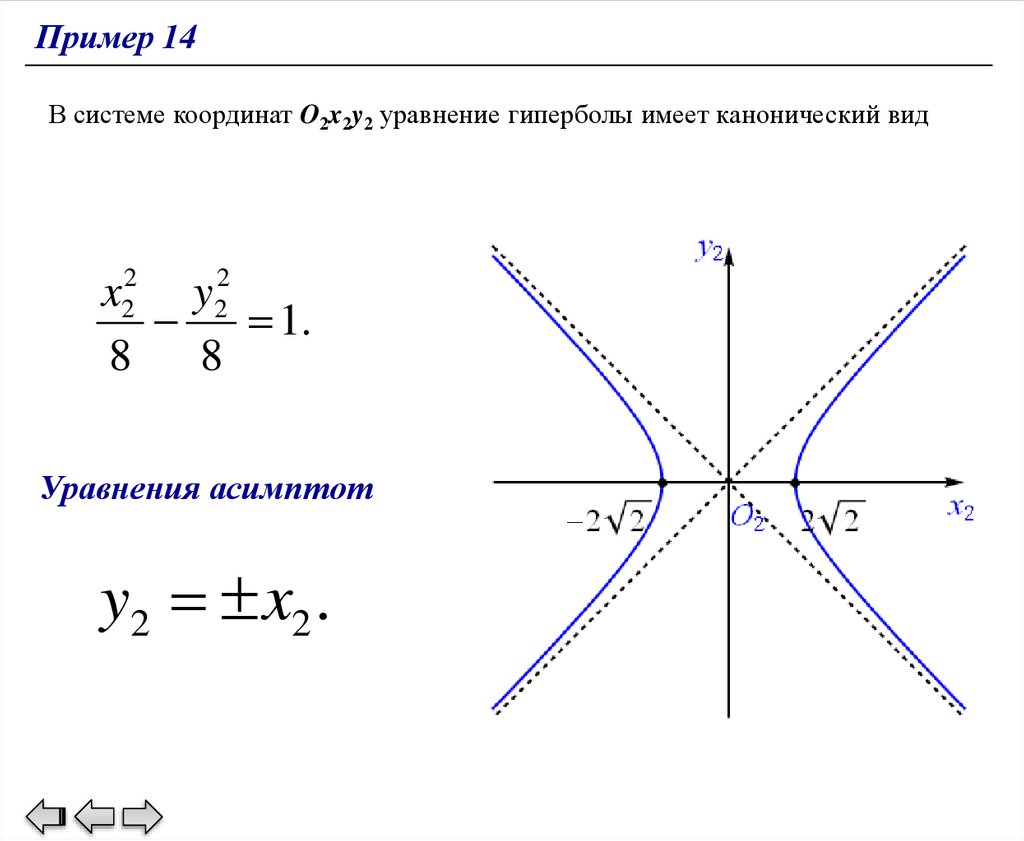
Пример 13В системе координат O2x2y2 уравнение эллипса имеет канонический вид
2
2
2
2
x
y
1.
8
2
94.
Пример 13Для того, чтобы построить эллипс, заданный в исходной системе координат Oxy
уравнением
5 x 2 6 xy 5 y 2 20 2 x 12 2 y 24 0,
поступаем следующим образом:
1. Изображаем исходную
систему
Oxy, а в ней
векторы e1 и e2 .
Эти векторы откладываем от
начала O системы координат,
они задают координатные
оси
новой
системы
координат Ox1y1.
95.
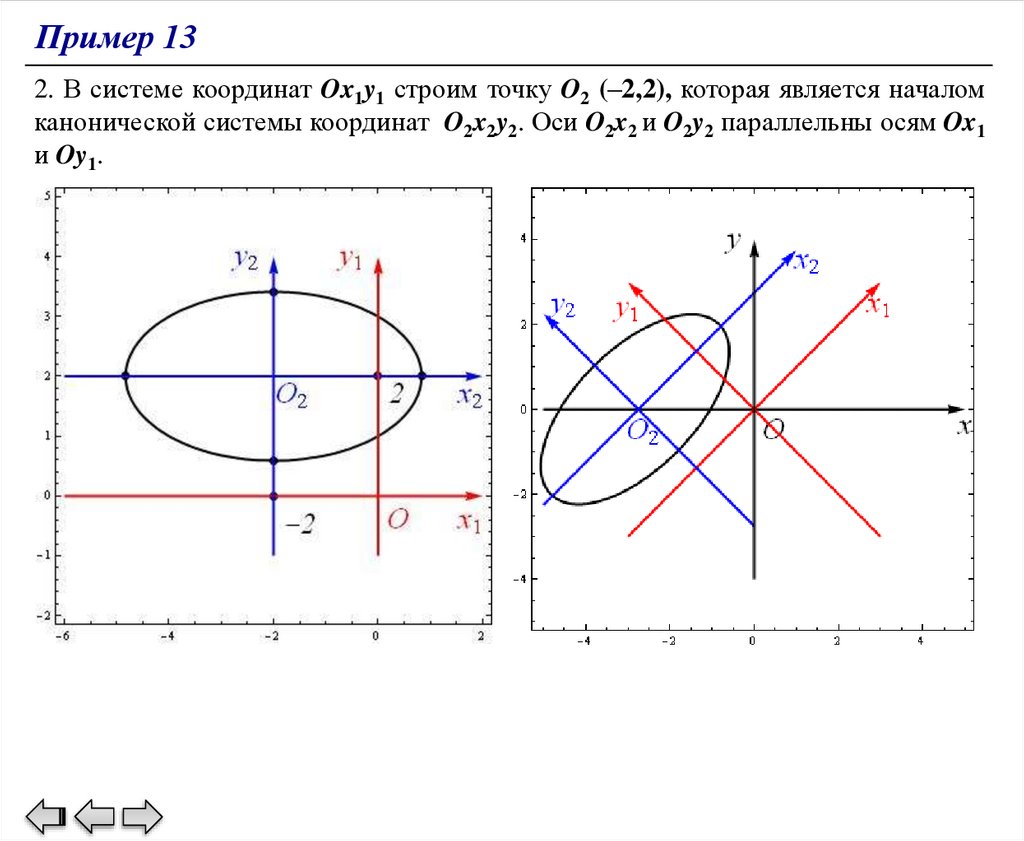
Пример 132. В системе координат Ox1y1 строим точку O2 (–2,2), которая является началом
канонической системы координат O2x2y2. Оси O2x2 и O2y2 параллельны осям Ox1
и Oy1.
96.
Пример 14Задание: Привести уравнение кривой второго порядка ортогональным
преобразованием и параллельным переносом к каноническому виду, указав
преобразования перехода от исходной прямоугольной системы координат Oxy к
полученной системе O2x2y2. Начертить кривую на плоскости Oxy, изобразив на
чертеже каноническую систему координат O2x2y2.
.
2
2
3x 8 xy 3 y 4 5 x 8 5 y 20 0.
Решение:
В матричном виде уравнение этой кривой второго порядка имеет вид
X T AX C T X 20 0,
где
3 4
,
A
4 3
Квадратичная форма имеет вид
4 5
C
,
8 5
x
X .
y
X T AX 3x 2 8xy 3 y 2 .
97.
Пример 14Найдём собственные числа и собственные векторы матрицы А квадратичной
T
2
2
формы X AX 3x 8xy 3 y .
3
4
4
3
25 0,
2
1 5,
2 5.
Собственному значению λ1= –5 соответствует единичный собственный вектор
1 1
,
e1
5 2
а собственному значению
λ2=5 соответствует единичный
собственный
вектор
1 2
. .
e2
5 1
98.
Пример 14Матрица ортогонального преобразования, приводящего квадратичную форму к
каноническому виду, составлена из столбцов координат собственных векторов.
Это преобразование является поворотом.
1
5
U
2
5
2
5 1 1 2
,
1
5 2 1
5
det U 1.
Этому ортогональному преобразованию соответствует линейная замена
переменных X UX 1
x1
x
U ,
y
y1
1
2
x
x
y1 ,
1
5
5
y 2 x 1 y .
1
1
5
5
99.
Пример 14После подстановки x и y в уравнение кривой получаем уравнение с квадратичной
формой канонического вида
2
2
2 2
1
1
1
3
x1
y1 8
x1
y1
x1
y1
5
5 5
5
5
5
2
1
2
3
x1
y1
5
5
2
1
1
2
4 5
x1
y1 8 5
x1
y1 20 0,
5
5
5
5
3 16 12 2 12 24 12
12 16 3 2
x1 y1 y1
x1
5
5
5 5 5
5
5 5 5
4 16 x1 8 8 y1 20 0,
5 x12 5 y12 20 x1 20 0.
100.
Пример 14Отметим, что канонический вид квадратичной формы мы можем записать сразу
по известным собственным числам
3x 2 8 xy 3 y 2 1 x12 2 y12 5 x12 5 y12 .
Порядок следования собственных чисел соответствует порядку собственных
векторов в матрице ортогонального преобразования – матрице перехода между
ортонормированными базисами систем координат Oxy и Ox1y1.
Линейные слагаемые преобразуются следующим образом.
Поскольку C T X C T UX 1 , то вектор-строка коэффициентов при линейных
слагаемых равен
1 2
1
CU
4 5 8 5
20 0 .
5
2 1
T
Свободный член останется прежним.
В результате уравнение поверхности в новых координатах принимает вид
5 x12 5 y12 20 x1 20 0.
После деления обеих частей уравнения на -5 получаем
x12 y12 4 x1 4 0.
.
101.
Пример 14По каждой из переменных выделяем полный квадрат
x 4x 4 4 y 4 0,
2
1
2
1
1
x1 2 y 8 0.
2
2
1
Преобразование параллельного переноса
x2 x1 2,
y2 y1
приводит к уравнению в системе координат O2x2y2, началом которой является
точка O2 (2,0)
x y 8 0.
2
2
2
2
Разделив обе части уравнения на 8, получаем каноническое уравнение
гиперболы
2
2
x2 y2
1.
8
8
102.
Пример 14В системе координат O2x2y2 уравнение гиперболы имеет канонический вид
x22 y22
1.
8
8
Уравнения асимптот
y2 x2 .
103.
Пример 14Для того, чтобы построить гиперболу, заданную в исходной системе координат Oxy
уравнением
3x 2 8 xy 3 y 2 4 5 x 8 5 y 20 0,
поступаем следующим образом:
1. Изображаем исходную
систему Oxy, а в ней векторы e1
и e2 .
Эти векторы откладываем от
начала O системы координат,
они задают координатные оси
новой системы координат
Ox1y1.
104.
Пример 142. В системе координат Ox1y1 строим точку O2 (2,0), которая является началом
канонической системы координат O2x2y2. Оси O2x2 и O2y2 параллельны осям
Ox1 и Oy1.
105.
Пример 15Задание: Привести уравнение кривой второго порядка ортогональным
преобразованием и параллельным переносом к каноническому виду, указав
преобразования перехода от исходной прямоугольной системы координат Oxy к
полученной системе O2x2y2. Начертить кривую на плоскости Oxy, изобразив на
чертеже каноническую систему координат O2x2y2.
16 x 24 xy 9 y 130 x 90 y 0.
2
2
Решение:
В матричном виде уравнение этой кривой второго порядка имеет вид
. 0,
X T AX C T X
где
130
16 12
A
, C 90 ,
12 9
Квадратичная форма имеет вид
x
X .
y
X T AX 16 x 2 24 xy 9 y 2 .
106.
Пример 15Найдём собственные числа и собственные векторы матрицы А квадратичной
формы X T AX 16 x 2 24 xy 9 y 2 .
16
12
12
9
25 0,
2
1 0,
2 25.
Собственному значению λ1=0 соответствует единичный собственный вектор
1 3
e1 ,
5 4
а собственному значению
λ2=25 соответствует единичный собственный вектор
1 4
e2 .
5 3
107.
Пример 15Матрица ортогонального преобразования, приводящего квадратичную форму к
каноническому виду, составлена из столбцов координат собственных векторов.
Это преобразование является поворотом.
3
5
U
4
5
4
5 1 3 4
,
3 5 4 3
5
det U 1.
Этому ортогональному преобразованию соответствует линейная замена
переменных X UX 1
x1
x
U ,
y
y1
3
4
x 5 x1 5 y1 ,
y 4 x 3 y .
1
1
5
5
108.
Пример 15После подстановки x и y в уравнение кривой получаем уравнение с
квадратичной формой канонического вида
2
4
4 4
3
3
3
16 x1 y1 24 x1 y1 x1 y1
5
5 5
5
5
5
2
3
4
3
4
3
4
9 x1 y1 130 x1 y1 90 x1 y1 0,
5
5
5
5
5
5
144 288 144 2 384 384 216 216
x1
x1 y1
25
25
25
25 25 25
25
256 288 81 2
y1 78 72 x1 (104 54) y1 0,
25 25
25
25 y12 150 x1 50 y1 0,
y12 6 x1 2 y1 0.
109.
Пример 15Отметим, что канонический вид квадратичной формы мы можем записать сразу
по известным собственным числам
16 x 2 24 xy 9 y 2 1 x12 2 y12 25 y12 .
Порядок следования собственных чисел соответствует порядку собственных
векторов в матрице ортогонального преобразования – матрице перехода между
ортонормированными базисами систем координат Oxy и Ox1y1.
Линейные слагаемые преобразуются следующим образом.
T
T
Поскольку C X C UX 1 , то вектор-строка коэффициентов при линейных
слагаемых равен
C TU
3 4
1
130
90
150 50 .
5
4 3
Свободный член отсутствует.
В результате уравнение поверхности в новых координатах принимает вид
25 y12 150 x1 50 y1 0.
После деления обеих частей уравнения на 25 получаем
y12 6 x1 2 y1 0.
.
110.
Пример 15Выделяем полный квадрат
1
y1 1 6 x1 .
6
2
Преобразование параллельного переноса
1
x2 x1 ,
6
y2 y1 1
приводит к уравнению в системе
координат O2x2y2, началом которой
является точка O2 (1/6,–1)
y 6 x2 .
2
2
В системе координат O2x2y2 уравнение параболы имеет канонический вид
111.
Пример 15Для того, чтобы построить параболу, заданную в исходной системе координат
Oxy уравнением
16 x 24 xy 9 y 130 x 90 y 0,
2
поступаем следующим образом:
1. Изображаем исходную
систему
Oxy, а в ней
векторы e и e2 .
1
Эти векторы откладываем
от начала O системы
координат,
они
задают
координатные оси новой
системы координат Ox1y1.
2
112.
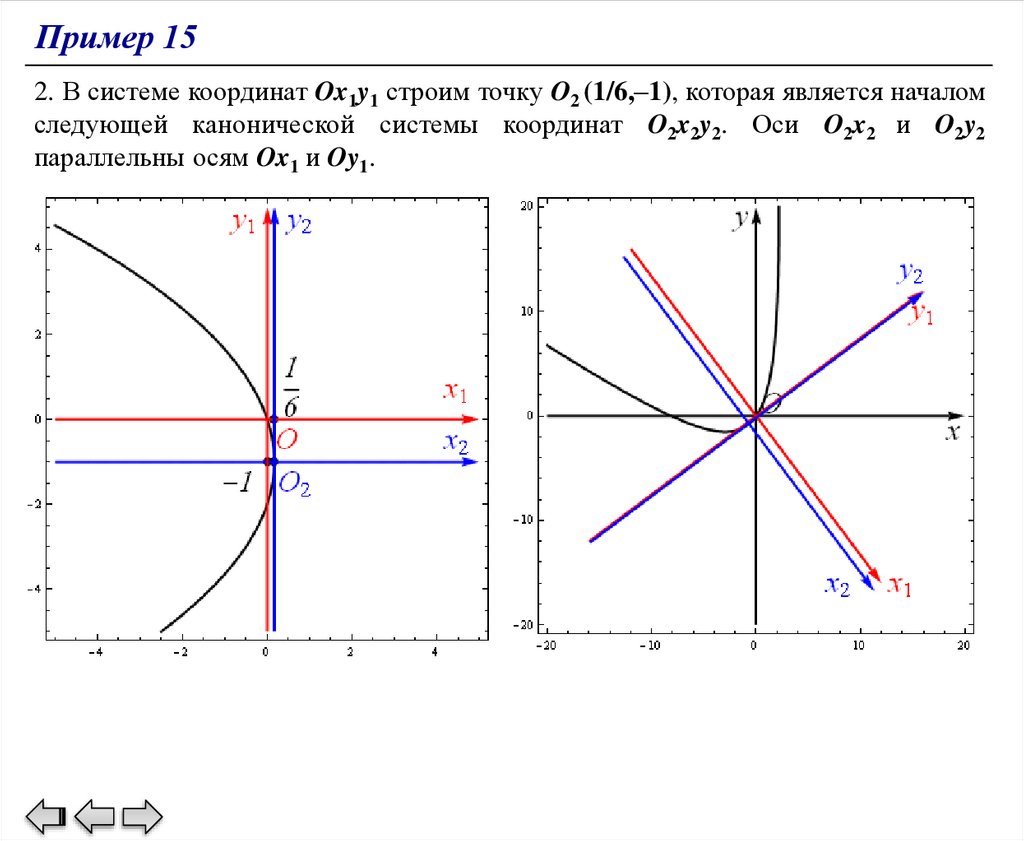
Пример 152. В системе координат Ox1y1 строим точку O2 (1/6,–1), которая является началом
следующей канонической системы координат O2x2y2. Оси O2x2 и O2y2
параллельны осям Ox1 и Oy1.
113.
Пример 16Задание: Привести уравнение поверхности второго порядка ортогональным
преобразованием и параллельным переносом к каноническому виду, указав
преобразование перехода от исходной прямоугольной системы координат Oxyz к
канонической системе координат O2x2y2z2. Построить поверхность в полученной
системе координат O2x2y2z2, используя метод сечений.
Все собственные числа матрицы A квадратичной формы расположить в порядке
возрастания, а матрицу ортогонального преобразования U построить так, чтобы
det U= +1.
7 x 2 6 y 2 5z 2 4 xy 4 yz 6 x 24 y 18z 30 0.
Решение:
В матричном виде уравнение этой поверхности второго порядка имеет вид
X T AX C T X 30 0,
где
7 2 0
6
x
A 2 6 2 , C 24 , X y .
0 2 5
.18
z
114.
Пример 16Найдём собственные числа и собственные векторы матрицы А квадратичной
T
2
2
2
формы X AX 7 x 6 y 5z 4 xy 4 yz.
7
det A E 2
2
0
6
2 3 18 2 99 162 0,
0
2
5
1 3,
2 6,
Собственным значениям λ1, λ2, λ3
векторы
1
1
e1 2 ,
3
2
3 9.
соответствуют единичные собственные
2
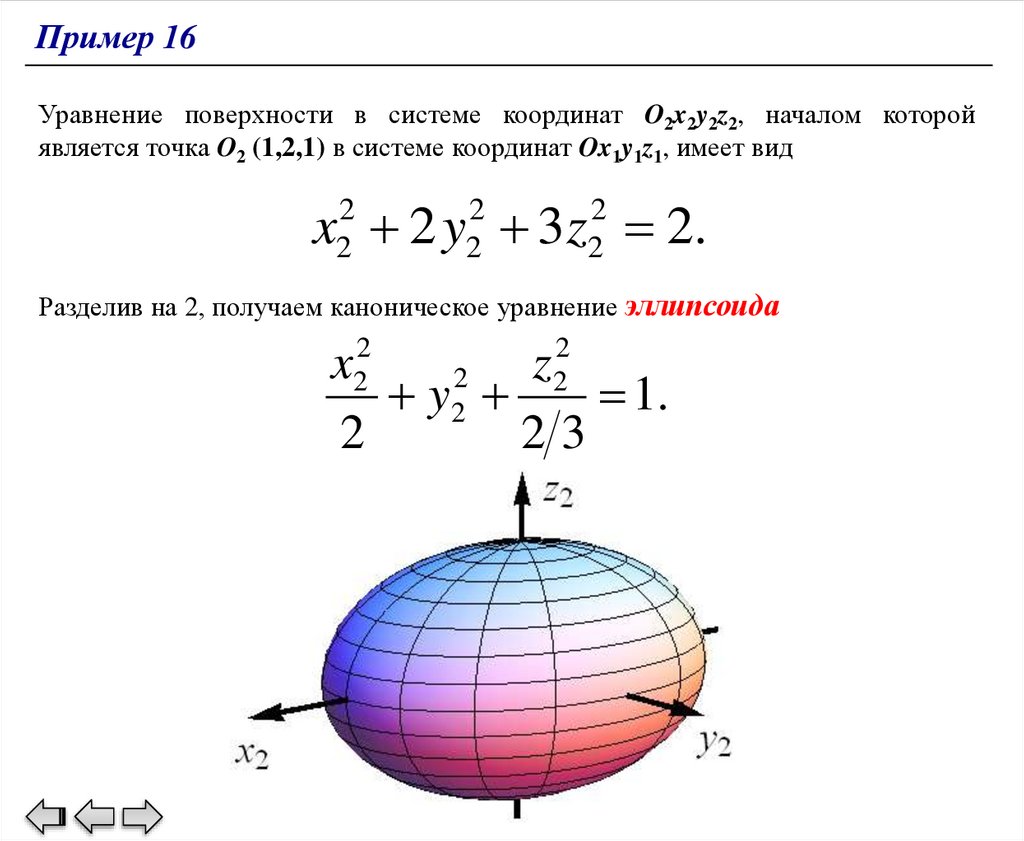
1
e2 1 ,
3
2
2
1
e3 2 .
3
1
115.
Пример 16Матрица ортогонального преобразования, приводящего квадратичную форму к
каноническому виду, составлена из столбцов координат собственных векторов.
Это преобразование является поворотом.
1 2 2
1
U 2 1 2 ,
3
2
2
1
Этому ортогональному
переменных X UX 1
преобразованию
x
x1
y U y1 ,
z
z
1
det U 1.
соответствует
линейная
1
2
2
x 3 x1 3 y1 3 z1 ,
2
1
2
y x1 y1 z1 ,
3
3
3
2
2
1
z 3 x1 3 y1 3 z1.
замена
116.
Пример 16Канонический вид квадратичной формы мы можем записать сразу по
известным собственным числам
7 x 2 6 y 2 5 z 2 4 xy 4 yz 1 x12 2 y12 3 z12 3x12 6 y12 9 z12 .
Порядок следования собственных чисел соответствует порядку собственных
векторов в матрице ортогонального преобразования – матрице перехода между
ортонормированными базисами систем координат Oxyz и Ox1y1z1.
Линейные слагаемые преобразуются следующим образом.
T
T
Поскольку C X C UX 1 , то вектор-строка коэффициентов при линейных
cлагаемых равен
1 2 2
C TU
1
6 24 18 2 1 2 6 24 18 .
3
2 2 1
Свободный член останется прежним.
В результате уравнение поверхности в новых координатах принимает вид
3x12 6 y12 9 z12 6 x1 24 y1 18 z1 30 0.
После деления обеих частей уравнения на 3 получаем
x12 2 y12 3z12 2 x1 8 y1 6 z1 10 0.
.
117.
Пример 16Таким образом, в новых координатах уравнение поверхности примет вид
x12 2 y12 3z12 2 x1 8 y1 6 z1 10 0.
По каждой из переменных выделяем полный квадрат
2
2
x
2
x
1
1
2
y
1 1
1 4 y1 4 8
3 z12 2 z1 1 3 10 0,
x1 1 2 y1 2 3 z1 1 2.
2
Параллельный перенос из
системы координат Ox1y1z1 в
O2x2y2z2
определен
соотношениями
2
2
x2 x1 1,
y2 y1 2,
z z 1.
1
2
118.
Пример 16Уравнение поверхности в системе координат O2x2y2z2, началом которой
является точка O2 (1,2,1) в системе координат Ox1y1z1, имеет вид
x22 2 y22 3z22 2.
Разделив на 2, получаем каноническое уравнение эллипсоида
2
x22
z
y22 2 1.
2
23
119.
Пример 17Задание: Привести уравнение поверхности второго порядка ортогональным
преобразованием и параллельным переносом к каноническому виду, указав
преобразование перехода от исходной прямоугольной системы координат Oxyz
к канонической системе координат O2x2y2z2. Построить поверхность в
полученной системе координат O2x2y2z2, используя метод сечений.
Во всех задачах собственные числа матрицы A квадратичной формы
расположить в порядке возрастания, а матрицу ортогонального
преобразования U построить так, чтобы det U= +1.
x 2 5 y 2 z 2 2 xy 2 yz 6 xz 2 x 6 y 2 z 0.
Решение:
В матричном виде уравнение этой поверхности второго порядка имеет вид
X T AX C T X 0,
где
1 1 3
A 1 5 1 ,
3 1 1
2
C 6 ,
. 2
x
X y .
z
120.
Пример 17Найдём собственные числа и собственные векторы матрицы А квадратичной
T
2
2
2
формы X AX x 5 y z 2 xy 2 yz 6 xz.
1
det A E 1
1
3
5
1
3
1
1
1 2,
2 3,
Собственным значениям λ1, λ2, λ3
векторы
1
1
e1
0 ,
2
1
3 7 2 36 0,
3 6.
соответствуют единичные собственные
1
1
e2
1 ,
3
1
1
1
e3
2 .
6
1
121.
Пример 17Матрица ортогонального преобразования, приводящего квадратичную форму к
каноническому виду, составлена из столбцов координат собственных векторов.
Это преобразование является поворотом.
3
2 1
1
U
2 2 ,
det U 1.
0
6
3
2
1
Этому ортогональному преобразованию соответствует линейная замена
переменных X UX 1
x
x1
y U y1 ,
z
z
1
1
x 6 3 x1 2 y1 z1 ,
1
2 y1 2 z1 ,
y
6
1
3 x1 2 y1 z1 .
z
6
122.
Пример 17Канонический вид квадратичной формы мы можем записать сразу по
известным собственным числам
x 2 5 y 2 z 2 2 xy 2 yz 6 xz 1 x12 2 y12 3 z12 2 x12 3 y12 6 z12 .
Порядок следования собственных чисел соответствует порядку собственных
векторов в матрице ортогонального преобразования – матрице перехода между
ортонормированными базисами систем координат Oxyz и Ox1y1z1.
Линейные слагаемые преобразуются следующим образом.
T
T
Поскольку C X C UX 1 , то вектор-строка коэффициентов при линейных
слагаемых равен
3
2 1
1
T
CU
2 6 2 0 2 2 2 2
6
3
2 1
2 3 2 6 .
Свободный член отсутствует.
В результате уравнение поверхности в новых координатах принимает вид
2 x12 3 y12 6 z12 2 2 x1 2 3 y1 2 6 z1 0.
123.
Пример 17По каждой из переменных выделяем полный квадрат
1
1
2
2 2
2 x1 2 x1 1 3 y1
y1 1
2
3
3
1
2 2
z1
z1 1 0,
6
6
2
2
2
1
1
1
2 x1
3 y1
6 z1
1.
2
3
6
124.
Пример 171
,
x2 x1
2
1
,
y2 y1
3
1
.
z
z
2
1
6
Параллельный перенос из
системы координат Ox1y1z1
в
O2x2y2z2
определен
соотношениями
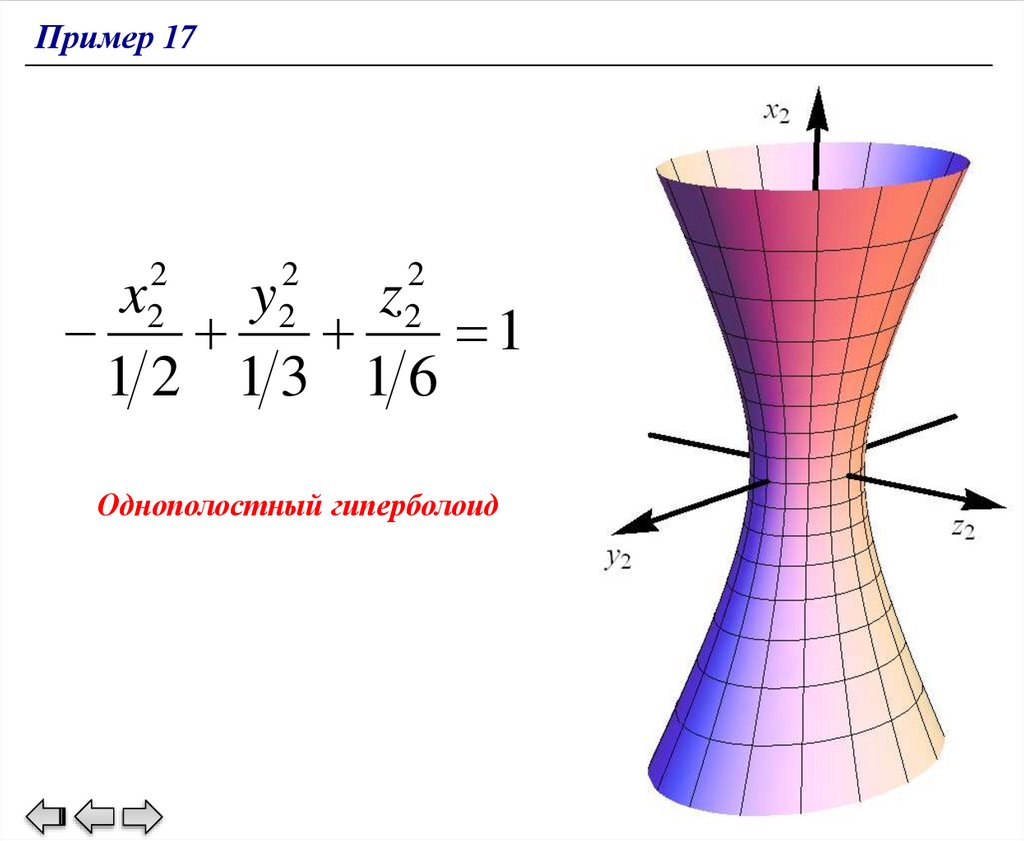
Он приводит к уравнению поверхности в системе координат O2x2y2z2, началом
которой является точка
Ox1y1z1,
O2 1
2 ,1
3 , 1
6 ,
заданная в системе координат
2 x22 3 y22 6 z22 1,
или, что тоже самое
В
итоге
мы
гиперболоида.
x22 y22 z22
1.
12 13 16
получили
каноническое
уравнение
однополостного
125.
Пример 172
2
2
2
2
2
x
y
z
1
12 13 16
Однополостный гиперболоид
126.
Пример 18Задание: Привести уравнение поверхности второго порядка ортогональным
преобразованием и параллельным переносом к каноническому виду, указав
преобразования перехода от исходной прямоугольной системы координат Oxyz
к канонической системе координат O2x2y2z2. Построить поверхность в
полученной системе координат O2x2y2z2, используя метод сечений.
Во всех задачах собственные числа матрицы A квадратичной формы
расположить в порядке возрастания, а матрицу ортогонального
преобразования U построить так, чтобы det U= +1.
2 x 2 2 y 2 5z 2 2 xy 2 x 4 y 4 z 2 0.
Решение:
В матричном виде уравнение этой поверхности второго порядка имеет вид
X T AX C T X 2 0,
где
2 1 0
A 1 2 0 ,
0 0 5
2
C 4 ,
. 4
x
X y .
z
127.
Пример 18Найдём собственные числа и собственные векторы матрицы А квадратичной
T
2
2
2
формы X AX 2 x 2 y 5 z 2 xy.
det A E
2
1
0
1
2
0
0
0
5
1 5,
2 1,
Собственным значениям λ1, λ2, λ3
векторы
0
e1 0 ,
1
3 2 17 15 0,
3 3.
соответствуют единичные собственные
1
1
e2
1 ,
2
0
1
1
e3
1 .
2
0
128.
Пример 18Матрица ортогонального преобразования, приводящего квадратичную форму к
каноническому виду, составлена из столбцов координат собственных векторов.
Это преобразование является поворотом.
0
1
U
0
2
2
Этому ортогональному
переменных X UX 1
1
1 1 ,
0 0
1
преобразованию
x
x1
y U y1 ,
z
z
1
det U 1.
соответствует
линейная
1
1
x
y
z1 ,
1
2
2
1
1
y
y
z1 ,
1
2
2
z x1.
замена
129.
Пример 18Канонический вид квадратичной формы мы можем записать сразу по
известным собственным числам
2 x 2 2 y 2 5 z 2 2 xy 1 x12 2 y12 3 z12 5 x12 y12 3z12 .
Порядок следования собственных чисел соответствует порядку собственных
векторов в матрице ортогонального преобразования – матрице перехода между
ортонормированными базисами систем координат Oxyz и Ox1y1z1.
Линейные слагаемые преобразуются следующим образом.
T
T
Поскольку C X C UX 1 , то вектор-строка коэффициентов при линейных
слагаемых равен
0
1
C TU
2
4
4
0
2
2
1
1 1 4
0 0
1
2
3 2 .
Свободный член остается прежним.
В результате уравнение поверхности в новых координатах принимает вид
5 x12 y12 3z12 4 x1 2 y1 3 2 z1 2 0.
130.
Пример 18По каждой из переменных выделяем полный квадрат
4 4 2
1 1
2 4
5 x1 x1 y1 2 y1
5
25 5
2 2
1 3
2
3 z1 2 z1 2 0,
2 2
2
2
2
2
1
1
4
5 x1 y1
3 z1
.
5
5
2
2
131.
Пример 18Параллельный перенос из
системы координат Ox1y1z1
в
O2x2y2z2
определен
соотношениями
2
x2 x1 ,
5
1
y
y
,
2
1
2
1
.
z 2 z1
2
Он приводит к уравнению поверхности в системе координат O2x2y2z2, началом
которой является точка O2 2 5 , 1
Ox1y1z1,
2 ,1
2 , заданная в системе координат
4
5 x y 3z .
5
2
2
2
2
2
2
Разделив на -4/5, получаем каноническое уравнение двуполостного
гиперболоида
x22
y22
z22
1.
4 2 5 4 5 4 15
132.
Пример 182
2
2
2
2
2
x
y
z
1.
4 2 5 4 5 4 15
Двуполостный
гиперболоид
133.
Пример 19Задание: Привести уравнение поверхности второго порядка ортогональным
преобразованием и параллельным переносом к каноническому виду, указав
преобразования перехода от исходной прямоугольной системы координат Oxyz
к канонической системе координат O2x2y2z2. Построить поверхность в
полученной системе координат O2x2y2z2, используя метод сечений.
Во всех задачах собственные числа матрицы A квадратичной формы
расположить в порядке возрастания, а матрицу ортогонального
преобразования U построить так, чтобы det U= +1.
7 x 2 7 y 2 16 z 2 10 xy 8 yz 8xz 16 x 16 y 8z 72 0.
Решение:
В матричном виде уравнение этой поверхности второго порядка имеет вид
X T AX C T X 72 0,
где
7 5 4
16
x
A 5 7 4 , C 16 , X y .
4 4 16
. 8
z
134.
Пример 19Найдём собственные числа и собственные векторы матрицы А квадратичной
формы X T AX 7 x 2 7 y 2 16 z 2 10 xy 8 yz 8 xz.
7
det A E 5
5
4
7
4 3 30 2 216 0,
4
4
16
1 0,
2 12,
Собственным значениям λ1, λ2, λ3
векторы
2
1
e1 2 ,
3
1
3 18.
соответствуют единичные собственные
1
1
e2
1 ,
2
0
1
1
e3
1 .
3 2
4
135.
Пример 19Матрица ортогонального преобразования, приводящего квадратичную форму к
каноническому виду, составлена из столбцов координат собственных векторов.
Это преобразование является поворотом.
2 2 3 1
1
U
det U 1.
2 2 3 1 ,
3 2
2
0
4
Этому ортогональному преобразованию соответствует линейная замена
переменных X UX 1
x
x1
y U y1 ,
z
z
1
2
1
1
x
x
y
z1 ,
1
1
3
2
3 2
2
1
1
y1
z1 ,
y x1
3
2
3 2
1
2 2
z1.
z x1
3
3
136.
Пример 19Канонический вид квадратичной формы мы можем записать сразу по
известным собственным числам
7 x 2 7 y 2 16 z 2 10 xy 8 yz 8 xz 1 x12 2 y12 3 z12 12 y22 18 z22 .
Порядок следования собственных чисел соответствует порядку собственных
векторов в матрице ортогонального преобразования – матрице перехода между
ортонормированными базисами систем координат Oxyz и Ox1y1z1.
Линейные слагаемые преобразуются следующим образом.
T
T
Поскольку C X C UX 1 , то вектор-строка коэффициентов при линейных
слагаемых равен
2 2
1
T
C U
16 16 8 2 2
3 2
2
3 1
3 1 24 0 0 .
0 4
Свободный член останется прежним.
В результате уравнение поверхности в новых координатах принимает вид
12 y22 18 z22 24 x2 72 0,
12 y22 18 z22 24 x2 3 .
137.
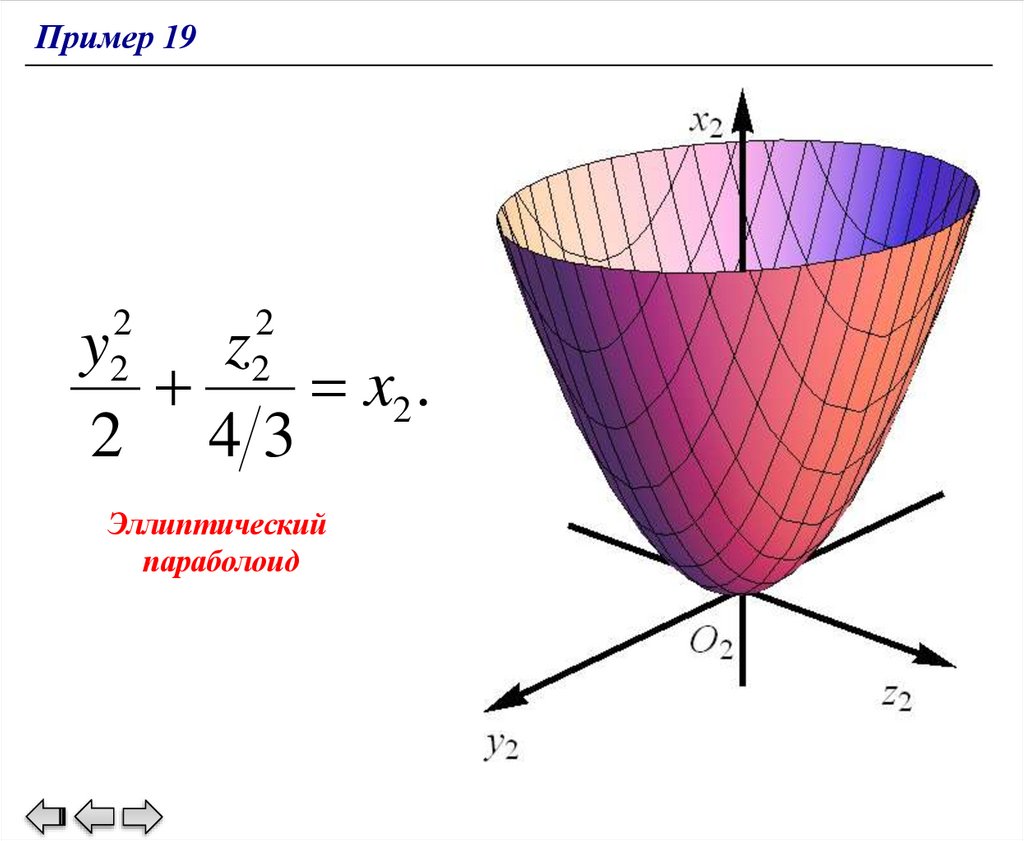
Пример 19x2 x1 3,
y2 y1 ,
z z .
2 1
Параллельный перенос из
системы координат Ox1y1z1
в
O2x2y2z2
определен
соотношениями
Он приводит к уравнению поверхности в системе координат O2x2y2z2, началом
которой является точка O2 (3,0,0), заданная в системе координат Ox1y1z1:
12 y 18 z 24 x2 .
2
2
2
2
Разделив на 24, получаем каноническое уравнение эллиптического
параболоида
2
2
2
2
y
z
x2 .
2 43
138.
Пример 192
2
2
2
y
z
x2 .
2 43
Эллиптический
параболоид
139.
Пример 20Задание: Привести уравнение поверхности второго порядка ортогональным
преобразованием и параллельным переносом к каноническому виду, указав
преобразования перехода от исходной прямоугольной системы координат Oxyz к
канонической системе координат O2x2y2z2. Построить поверхность в полученной
системе координат O2x2y2z2, используя метод сечений.
Все собственные числа матрицы A квадратичной формы расположить в порядке
возрастания, а матрицу ортогонального преобразования U построить так, чтобы
det U= +1.
2 x 2 7 y 2 4 z 2 4 xy 20 yz 16 xz 60 x 12 y 12 z 90 0.
Решение:
В матричном виде уравнение этой поверхности второго порядка имеет вид
X T AX C T X 90 0,
где
2 8
2
60
x
A 2 7 10 , C 12 , X y .
8 10 4
.12
z
140.
Пример 20Найдём собственные числа и собственные векторы матрицы А квадратичной
T
2
2
2
формы X AX 2 x 7 y 4 z 4 xy 20 yz 16 xz.
det A E
2
2
8
2
7
10
8
10
4
1 18,
2 0,
Собственным значениям λ1, λ2, λ3
векторы
1
1
e1 2 ,
3
2
3 9 2 162 0,
3 9.
соответствуют единичные собственные
2
1
e2 2 ,
3
1
2
1
e3 1 .
3
2
141.
Пример 20Матрица ортогонального преобразования, приводящего квадратичную форму к
каноническому виду, составлена из столбцов координат собственных векторов.
Это преобразование является поворотом.
1 2 2
1
U 2 2 1 ,
3
2
1
2
Этому ортогональному
переменных X UX 1
преобразованию
x
x1
y U y1 ,
z
z
1
det U 1.
соответствует
линейная
1
2
2
x 3 x1 3 y1 3 z1 ,
2
2
1
y
x
y
z1 ,
1
1
3
3
3
2
1
2
z 3 x1 3 y1 3 z1.
замена
142.
Пример 20Канонический вид квадратичной формы мы можем записать сразу по
известным собственным числам
2 x 2 7 y 2 4 z 2 4 xy 20 yz 16 xz 1 x12 2 y12 3 z12 18 x12 9 z12 .
Порядок следования собственных чисел соответствует порядку собственных
векторов в матрице ортогонального преобразования – матрице перехода между
ортонормированными базисами систем координат Oxyz и Ox1y1z1.
Линейные слагаемые преобразуются следующим образом.
T
T
Поскольку C X C UX 1
то вектор-строка коэффициентов при линейных
слагаемых равен
1 2 2
C TU
1
60 12 12 2 2
3
2 1
1 36 36 36 .
2
Свободный член остается прежним.
В результате уравнение поверхности в новых координатах принимает вид
18x12 9 z12 36 x1 36 y1 36 z1 90 0.
После деления обеих частей уравнения на 9 получаем
2
2
1
1
1
1
1
2 x z 4 x 4 y 4 z 10 0.
.
143.
Пример 20По каждой из переменных выделяем полный квадрат
2 x12 2 x1 1 2 z12 4 z1 4 4
4 y1 10 0,
2 x1 1 z1 2 4 y1 3 0.
2
2
Параллельный перенос из системы координат Ox1y1z1 в O2x2y2z2 определен
соотношениями
x2 x1 1,
y2 y1 3,
z z 2.
1
2
144.
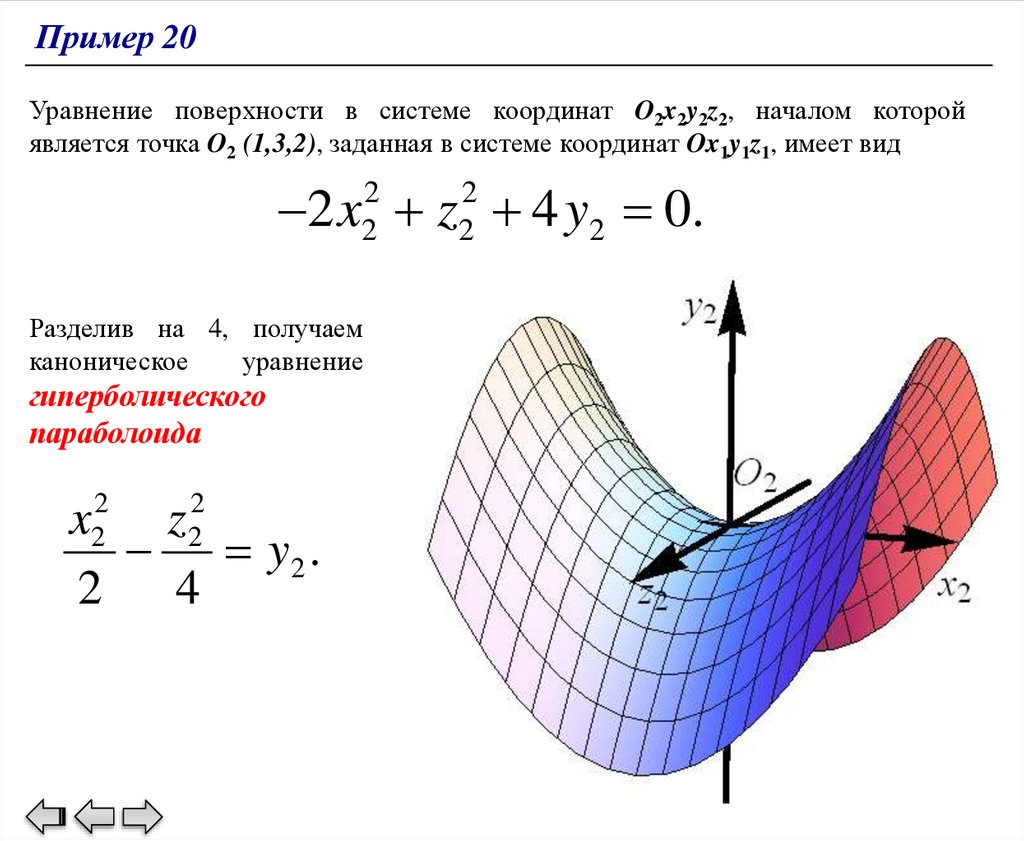
Пример 20Уравнение поверхности в системе координат O2x2y2z2, началом которой
является точка O2 (1,3,2), заданная в системе координат Ox1y1z1, имеет вид
2 x z 4 y2 0.
2
2
Разделив на 4, получаем
каноническое
уравнение
гиперболического
параболоида
2
2
2
2
x
z
y2 .
2 4
2
2
145.
ЛитератураОсновная литература
1. Канатников А.Н., Крищенко А.П. Аналитическая геометрия: Учеб. для вузов
2-е изд. / Под ред. B.C. Зарубина, А.П. Крищенко. – М., Изд. МГТУ, 2000. –
388 с. (Сер. Математика в техническом университете, вып. III).
2. Канатников А.Н., Крищенко А.П. Линейная алгебра: Учеб. для вузов / Под
ред. B.C. Зарубина, А.П. Крищенко. – М.: Изд-во МГТУ им. Н.Э. Баумана,
2006. – 336 с. (Сер. Математика в техническом университете, вып. IV).
3. Ильин В.А., Позняк Э.Г. Аналитическая геометрия. – М.: Физматлит, 2003. –
240 с.
4. Ильин В.А., Позняк Э.Г. Линейная алгебра. – М.: Физматлит, 2003. – 296 с.
5. Задачи и упражнения по математическому анализу для втузов / Под ред. Б.П.
Демидовича. – М.: Интеграл-Пресс, 1997. – 416 с.
6. Сборник задач по математике для втузов. Ч. 1. Линейная алгебра и основы
математического анализа: Учеб. пособие для втузов / Под ред. А.В.
Ефимова, Б.П. Демидовича. – М.: Наука, 1993. – 478 с.
Дополнительная литература
1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. – М.:
Наука, 1987. – 336 с.
2. Беклемишева Л.А., Петрович Ю.А., Чубаров И.А. Сборник задач по
аналитической геометрии и линейной алгебре. – М.: Наука, 1987. – 496 с.
146.
Литература3. Вся высшая математика: Учебник для втузов: В 6 т. / Краснов М.Л., Киселев
А.И., Макаренко и др. – Т. 1. – М.: Эдиториал УРСС, 2000. – 327 с.
4. Клетеник Д.В. Сборник задач по аналитической геометрии. – Спб.:
Профессия, 2001. – 240 с.
5. Сборник задач по линейной алгебре / Под ред. С.К. Соболева. – М.: МГТУ,
1991. –154 с.
Методические пособия, изданные в МГТУ
Бархатова О.А., Садыхов Г.С. Поверхности второго порядка. – М.: Изд-во
МГТУ им. Н.Э. Баумана, 2005. – 40 с.
Гришина Г.В., Козлов М.Е., Пашовкин Е.М., Подобряев В.Н. Методические
указания к самостоятельной работе студентов по разделам «Математический
анализ» и «Линейная алгебра», под ред. Гришиной Г.В. Учеб. пособие. – М.:
МГТУ, 1990.–38 с.
Дубограй И.В., Леванков В.И., Максимова Е.В. Методические указания к
выполнению домашнего задания по теме «Кривые второго порядка». – М.:
Изд-во МГТУ им. Н.Э. Баумана, 2002. – 52 с.
Пугачев О.В., Стась Г.П., Чередниченко А.В. Квадратичные формы и их
геометрические приложения. Методические указания к выполнению
типового расчета. – М.: МГТУ, 2004. – 59 с.































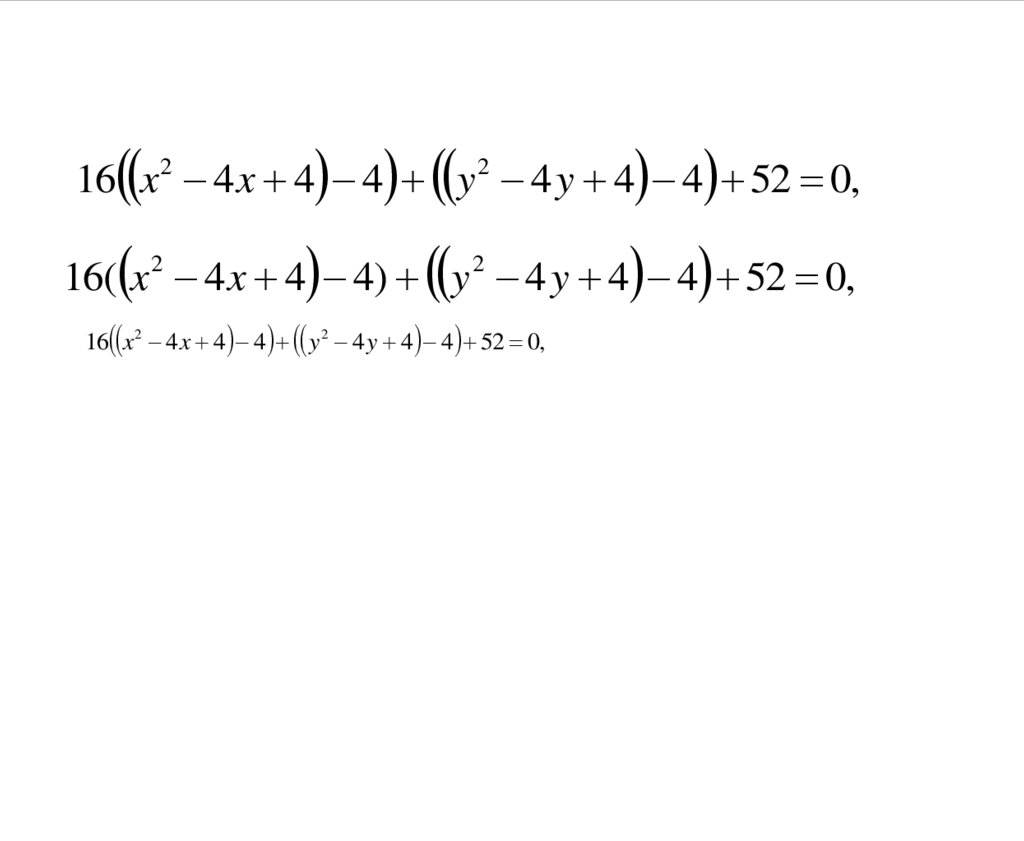







































































 mathematics
mathematics








